基于動態估計誤差的中國股市波動率建模與預測

宋亞瓊，王新軍

(1.中共泰安市委黨校，山東 泰安 271000；2.山東大學經濟學院，山東 濟南 250100)

基于動態估計誤差的中國股市波動率建模與預測

宋亞瓊1，王新軍2

(1.中共泰安市委黨校，山東 泰安 271000；2.山東大學經濟學院，山東 濟南 250100)

本文設波動率的估計誤差服從異方差假定，在對已實現波動率進行建模時，根據方差變化來設定模型的自回歸系數，構建基于高頻數據的HARQ(F)模型。在此基礎上，考慮中國股市波動的跳躍行為及杠桿效應，先后構建了HARQ(F)-CJ模型和LHARQ(F)-CJ模型，以改善波動率模型的擬合效果和預測能力。本文假設，當期已實現波動率或其連續成分的估計誤差的方差越大，它對未來真實波動率的解釋力度則越差，因而其對應系數越小。對上證綜合指數近15年的五分鐘高頻數據進行實證研究發現，基于估計誤差異方差假定的動態系數能夠提高已實現波動率模型的擬合效果和預測能力。其中，對日回歸系數進行基于估計誤差方差的動態調整是模型改進的關鍵。同時考慮中國股市波動的跳躍行為及杠桿效應的LHARQ-CJ模型在所有模型中表現最優。

已實現波動率；動態估計誤差；高頻數據；跳躍行為；杠桿效應

1 引言

股市波動率的建模與預測一直以來是金融理論研究的重要命題之一。它對資產組合選擇、金融資產及其衍生品定價、以及金融機構的風險管理都具有重要意義。20世紀80年代起，國內外學者提出了基于低頻數據的GARCH類模型和SV類模型對股市波動率進行估計和預測，很好地刻畫了股市波動的集聚性和時變性特點。進入21世紀，基于高頻數據的股市波動率的建模與預測成為新的研究趨勢。為了充分利用股市交易的日內信息，Andersen和Bollerslev[1]提出了基于高頻交易數據的已實現波動率(Realized Volatility，RV)，作為股票市場真實波動率的一致估計量。在此基礎上，Andersen等[2]結合波動率的長記憶性構建了ARFIMA-RV模型，Corsi[3]綜合考慮了波動率的長記憶性和異質性，建立了HAR-RV模型。通過實證研究發現，ARFIMA-RV模型和HAR-RV模型對股市波動率的樣本外預測能力優于傳統的GARCH模型和SV模型，而HAR-RV模型因其簡單有效的形式得到廣泛應用。魏宇[4]將已實現波動率作為附加解釋變量加入GARCH模型和SV模型中，運用SPA檢驗進行評估發現，模型的預測能力有所提高。

隨著HAR-RV模型的廣泛應用，國內外研究者結合股市波動的諸多性質對其進行了擴展研究。Andersen等[5]基于多次冪變差理論將已實現波動率分解為連續成分和跳躍成分，在此基礎上構建HAR-J模型和HAR-CJ模型，通過實證研究發現，這兩種成分對波動率預測都有顯著影響，提高了模型預測能力。Bollerslev等[6]綜合考慮了股市波動的跳躍行為和杠桿效應，提出HAR-GARCH-BV模型，并結合收益率方程和跳躍方程提高了波動率預測水平。Corsi[7]構建LHAR-CJ模型，證明股市波動的跳躍行為和股價負收益能夠影響股市波動預測。陳浪南和楊科[8]結合中國股市高頻波動率的長記憶性、結構突變、不對稱性和周內效應等特征，構建了自適應的不對稱性HAR-CJ-D-FIGARCH模型，通過實證研究發現，該模型對中國股市的波動有很好的擬合效果和預測能力。孫潔[9]將日波動率劃分為跳躍性波動、連續性波動和隔夜波動，建立HAR-CJN模型對股市波動率進行預測，提升了模型的預測能力。

在日內高頻數據抽樣頻率足夠高的情形下，已實現波動率為股市真實波動積分波動率(Integrated Volatility，IV)的一致估計量。當抽樣有限時，研究者將RV與IV之間的偏差定義為估計誤差，由微觀結構噪聲和其他測量偏差導致。當估計誤差越大時，已實現波動率對股市真實波動的估計和預測就越不準確。隨著研究的深入，估計誤差開始成為國內外學者基于RV進行股市波動率建模和預測的新關注點。Asai等[10]運用蒙特卡羅模擬法研究了使用RV估計股市波動時的誤差，發現忽略估計誤差會導致由模型誤設而引起的嚴重偏差。Dobrev和Szerszen[11]提出了狀態空間形式的漸進精確波動率測量方程，運用貝葉斯估計方法，將RV的估計誤差方差考慮在內對股市波動率進行建模和預測，但這種方法沒有將估計誤差方差設為模型的動態變量。

近年來，考慮微觀結構噪聲引起的估計誤差的波動率建模研究開始起步。為了降低微觀結構噪聲引起的估計誤差，Jacod等[12]提出預平均法，運用連續函數對高頻數據進行光滑處理，經證明，這種方法能夠對積分波動率的估計量漸進方差進行一致估計。Andersen等[13]在運用隨機波動模型來估計股市波動率時，選擇了多種形式的已實現波動率測量量，其中基于平均標準稀疏抽樣方法的已實現波動率在建模和預測中表現最好。Bandi等[14]提出了基于時變抽樣頻率的已實現波動率估計量，用來解釋由市場微觀結構噪聲而造成的估計誤差中的異方差性，為股市波動預測提供了更強的有效信息。國內研究中，唐勇[15]將已實現波動分解為連續樣本路徑方差、跳躍方差和微觀結構噪聲方差，提出HAR-N-CJ模型和LHAR-N-CJ模型，實證結果表明新模型在擬合與預測方面都較HAR-CJ模型有所提高。馬丹和尹優平[16]提出，門限預平均實現波動能夠在微觀結構噪聲和波動跳躍同時存在的情況下減少股市波動的預測誤差，是資產價格波動的一致估計。

綜上所述，基于已實現波動率的股市波動建模和預測研究發展日臻完善，近些年，學者們開始關注已實現波動率的估計誤差對建模和預測的影響。然而，現有研究對估計誤差中由市場微觀結構噪聲引起的部分研究偏多，考慮估計誤差總體效果的文獻較少。在結合估計誤差的波動率建模研究中，也沒有將其方差的動態性體現在模型中。本文將RV估計誤差的方差變化設為影響模型預測結果的因素，在對已實現波動率進行建模時根據基于估計誤差的異方差假定來設定模型系數，提出了HARQ(F)模型，以及結合中國股市波動的跳躍行為和杠桿效應的HARQ(F)-CJ模型和LHARQ(F)-CJ模型，從而改善已實現波動率模型的擬合效果和預測能力。

2 動態系數的波動率建模理論

2.1已實現波動率和高頻分布理論

假設資產價格服從如下隨機差分方程：

dln(Pt)=μtdt+σtdWt

(1)

其中，μt表示飄移項，σt表示瞬時波動率，Wt為獨立于σt的標準布朗運動。定義資產價格在t期的真實波動率為積分波動率IV(Integrated Volatility)。

(2)

已實現波動率RV(Realized Volatility)是資產價格n個日內收益率的平方和。

(3)

其中，Δ表示資產價格數據的抽樣間隔。M=1/Δ，表示日內收益率的數目。rt,i≡100×[logPt+iΔ-logPt+(i-1)Δ]表示Δ時段內的收益率。

根據Barndorff-Nielsen和Shephard[17]提出的漸進分布理論，當抽樣間隔Δ→0時，真實波動率可由已實現波動率進行一致估計，估計誤差設為ηt。

RVt=IVt+ηt，ηt～N(0,2ΔIQt)

(4)

2.2估計誤差的異方差假定

RV是真實波動率的一致估計量，同時，估計誤差在一般情況下是序列不相關的。因此，我們可以用含RV的時間序列模型來預測潛在的真實波動率。

假設IV的動態相依關系可以由如下AR(1)模型表示：

IVt=φ0+φ1IVt-1+μt

(5)

(6)

現在假設，以AR(1)過程來代替ARMA(1,1)過程對RV進行擬合，有下式成立：

IVt+ηt=β0+β1(IVt-1+ηt-1)+μt

(7)

等式左側的估計誤差ηt影響的是估計參數的標準差，而等式右側的估計誤差ηt-1會直接影響參數β1的估計，從而對模型預測產生影響。

(8)

以上論述是基于估計誤差的方差是常數的假設，然而，從式(4)可以看出，RV對真實波動率的估計誤差隨著時間的變化而改變。當IQ較小時，RV對IV的估計較為精確；當IQ較大時，估計效果減弱。因此，從預測的角度上講，AR模型的常系數假定并不是最優的，本文構造隨時間變化的自回歸系數β1,t來擬合IQ變化對估計的影響。

(9)

(10)

將系數β1,t代入RV的自回歸模型可得模型(10)。筆者將RV模型的自回歸系數看作是IQ1/2估計量的線性函數，而沒有直接采用式(8)中方差的倒數形式，是為了使模型更加穩健。同時，模型還能夠用簡單的OLS方法進行估計。模型的自回歸系數β1,t隨估計誤差的方差而變化。特別地，假定β1,Q<0，當該日RV作為真實波動率的估計量誤差較大時，它對未來真實波動率的預測作用較弱，而估計誤差較小的RV對未來真實波動率的預測起到較強的解釋作用。這就是本文建模的理論基礎。

3 基于跳躍行為和杠桿效應的模型擴展

3.1HARQ模型

模型(10)作為一階自回歸模型無法描述RV對真實波動率預測的長記憶性，本文結合估計誤差的異方差假定，對異質自回歸模型HAR-RV進行改進，得到如下模型：

(11)

同理，該模型日、周和月的自回歸系數受到相應RV估計誤差的影響，它們隨著平均估計誤差的增大而減小，從而使得具有較大估計誤差的RV對未來真實波動率預測作用降低。我們將此模型稱為HARQF模型。

隨著時間跨度k的增大，平均估計誤差RQt-1|t-k的解釋作用會隨之弱化。所以，根據估計誤差調整的日系數對波動率的解釋能力要高于調整的周系數和月系數。據此，本文對模型(11)進行簡化處理，僅對具有較強解釋能力的日系數根據估計誤差進行調整，定義了HARQ模型。

(12)

3.2HARQ-CJ模型

當資產價格發生跳躍時，它服從以下隨機差分方程。

dln(Pt)=μtdt+σtdWt+κtdNt

(13)

本文用以下Z統計量對波動跳躍的存在性進行檢驗。

Zt≡

(14)

當Zt大于標準正態分布在顯著性水平為α的臨界值Φα時，我們認為存在波動率跳躍，Jt≡I(Zt>Φα)·[RVt-BPVt]，波動的連續成分為Ct≡I(Zt≤Φα)·RVt+I(Zt>Φα)·BPVt，I(·)為示性函數。

Barndorff-Nielsen和Shephard[17]指出，若用BPV來估計真實波動率，其估計誤差的漸進方差為2.61ΔIQt，而在積分變差IQ的一致估計量中，已實現三次冪變差TPQ在跳躍存在的情形下是有效的。

基于此，本文對HAR-CJ模型進行改進，使其滿足估計誤差的異方差假定，將波動率連續成分的系數看作是隨估計誤差方差的變化而改變的。形式如下：

(15)

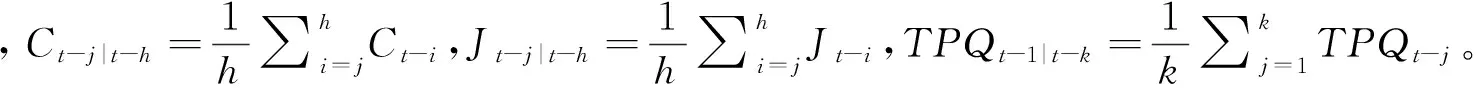
該模型連續成分的日、周和月自回歸系數受到相應已實現波動率連續成分的估計誤差影響，它們隨著平均估計誤差的增大而減小，從而使得具有較大估計誤差的連續成分對未來真實波動率預測作用降低。該模型還同時刻畫了跳躍成分的日、周和月效應對未來波動率預測的作用。我們將此模型稱為HARQF-CJ模型。

同理，隨著時間跨度k的增大，平均估計誤差TPQt-1|t-k的解釋作用會隨之弱化。本文定義了HARQ-CJ模型，僅對具有較強解釋能力的連續成分日系數根據估計誤差進行調整。

(16)

3.3LHARQ-CJ模型

杠桿效應是股市波動率的特點之一。具體表現為，在股票市場中，同等程度的負面沖擊比正面沖擊能夠引起更大的股價波動。中國股市實行嚴格的賣空限制的交易制度，使得中國股市波動率的杠桿效應具有持續性特點。因此，我們結合Corsi(2009)提出的LHAR-CJ模型，考慮前期不同周期的負收益對未來真實波動率預測的影響，進一步構建LHARQF-CJ模型和LHARQ-CJ模型，以增強估計誤差異方差假定的適用性。

(17)

(18)

本文構建HARQ(F)模型、HARQ(F)-CJ模型和LHARQ(F)-CJ模型，選擇非線性最小二乘法，使用穩健的標準誤差進行估計。通過對模型系數顯著性及模型損失函數的分析，來驗證基于估計誤差異方差假定的動態系數是否能夠提升波動率模型的預測能力，為股價真實波動率的預測提供更好的理論模型。

4 實證研究

4.1數據與分析

本文選取上證綜合指數2001年1月2日至2015年12月31日的五分鐘高頻數據作為樣本，有效數據為3843組。選擇99%的置信區間，對波動率的跳躍成分和連續成分進行檢驗和計算。為了更加直觀地分析，對上證指數的負收益取絕對值處理。表1為模型所涉及變量的統計性質，圖1對模型解釋變量與被解釋變量之間的相關關系進行了判斷。

表1 變量描述性統計表

圖1 已實現波動率與變量間的相關系數圖

本文檢測了已實現波動率的自相關系數，以及它與股價指數的正負收益以及跳躍成分之間的相關系數。如圖1所知，已實現波動率呈現出一定的長記憶性，其自相關程度隨時間呈緩慢遞減。已實現波動率與指數正、負收益的絕對值之間表現出一定的正相關性，相比來看，負收益對已實現波動率的相關系數更大，且相關性曲線的衰減較為平穩。這說明，指數的負收益對已實現波動率的影響作用更大，上證指數的波動具有杠桿效應，利空消息對波動的影響要大于利好消息對波動的影響。同時，這種杠桿效應還具有一定的持續性，并隨著滯后期的增加而逐漸減弱，這是杠桿效應對波動率的異質性影響。由圖2可知，波動的跳躍成分對已實現波動率也有一定程度的異質性影響。由此可見，我們在動態估計誤差模型中添加杠桿效應和跳躍成分的不同期滯后影響，對上證綜指的波動率預測具有重要意義。

4.2樣本內估計

本文使用上證綜合指數3843組有效數據，對HARQ(F)模型、HARQ(F)-CJ模型和LHARQ(F)-CJ模型進行樣本內估計，擬合結果如下表所示。為了比較波動率模型的擬合效果，選擇經典的ARMA(1,1)模型、HAR模型、HAR-CJ模型和LHAR-CJ模型作為參照。

圖2所示為HAR模型和HARQ模型對上證綜指2015年8月份十個連續交易日的波動率擬合結果對比圖。圖(a)為已實現波動率及其基于(4)式所估計的95%置信區間，其中，8月26日的已實現波動率相比其他交易日更大，且從置信區間寬度來看，其估計誤差較大，估計結果更不精確。圖(b)為β1和β1,t的估計結果，可見，在“正常”波動的交易日中，HARQ模型中的β1,t系數在0.5～0.6之間，而HAR模型中β1系數僅為0.35，在RV估計較為不精確的8月26日，系數β1,t均降為0.26。圖(c)為兩個模型對向前一期波動率的預測結果與真實值的對比，由圖可知，在HAR模型中，8月26日的RV拉高了下一個交易日的波動率預測結果；而在HARQ模型中，系數β1,t的降低使得下一個交易日的波動率預測結果較少地收到8月26日高波動率的影響，更加接近當期RV的值。由此可見，當某個交易日RV的估計誤差變大時，HARQ模型比HAR模型對未來真實波動率的預測更加精確。

表2 模型擬合結果

注：***、**、*分別表示在1%、5%和10%水平上顯著相關；括弧中為p值。

圖2 HAR模型和HARQ模型擬合結果對比圖

表3 樣本外預測損失函數比較

注：***、**、*分別表示在1%、5%和10%水平上顯著相關；括弧中為p值。

4.3樣本外預測

為了考察模型的預測能力，本文采用滾動時間窗預測(Rolling Window)和遞增時間窗預測(Increasing Window)兩種方式，考察模型對向前一期波動率的預測結果。其中，滾動時間窗的樣本長度固定為1000個交易日，從第1001個交易日的預測開始，每一期的預測結果都是基于前1000個樣本數據。遞增時間窗的樣本長度隨時間變化從1000個交易日遞增到3842個，從第1001個交易日的預測開始，每一期的預測結果都是基于前面所有的樣本數據。本文選用均方誤差的開方(RMSE)和平均絕對誤差(MAE)兩種損失函數作為比較模型預測能力的方法，并以Giacomini-White檢驗統計量的p值來說明不同模型間的預測能力差異是否顯著。表3展示了以HAR模型作為比較基準，不同模型與它之間損失函數的比值。

首先，從對所有模型進行滾動時間窗預測和遞增時間窗預測的RMSE值和MAE值來看，基于動態估計誤差的系數模型表現優于傳統的ARMA模型和HAR模型，說明已實現波動率及其連續成分的估計誤差異方差假定可以提高模型的預測能力。其次，除一組數據外，僅對日系數進行估計誤差異方差調整的HARQ、HARQ-CJ與LHARQ-CJ模型在同類模型中表現最好。雖然在樣本內估計中，HARQF、HARQF-CJ與LHARQF-CJ模型的擬合結果與其相差不大，但樣本外預測能力存在差距。這說明，基于估計誤差異方差假定的動態系數模型可以提高模型的預測能力，并且，無論是對于已實現波動率還是其連續成分，對滯后一期的系數(即日系數)的調整是提高模型預測能力的關鍵。最后，在兩種不同的預測方法和損失函數下，含有波動率連續成分和跳躍成分的動態系數模型優于已實現波動率的動態系數模型，再考慮杠桿效應的模型表現更優之。其中，LHARQ-CJ模型在三種情形中預測能力都是最優的。這說明，在基于估計誤差異方差假定的動態系數模型中考慮跳躍和杠桿效應，可以提高模型的預測能力。

5 結語

本文設波動率的估計誤差服從異方差假定，基于此得到隨誤差方差變化的自回歸系數，從而構建HARQ(F)模型來估計已實現波動率。進一步，在動態系數模型中結合波動的連續成分、跳躍成分及杠桿效應，提出了HARQ(F)-CJ和LHARQ(F)-CJ模型。本文以上證綜合指數2001年1月2日至2015年12月31日的五分鐘高頻數據作為樣本進行實證研究，得出的結論如下：

第一，基于估計誤差異方差假定的動態系數能夠提高已實現波動率模型的擬合效果和預測能力。當期已實現波動率或其連續成分的估計誤差的方差越大，則當期已實現波動率或其連續成分在模型中的系數越小，它對未來真實波動率的解釋力度則越差。這種動態系數的性質使得HARQ(F)、HARQ(F)-CJ和LHARQ(F)-CJ模型對于未來真實波動率的預測能力有了顯著提升。

第二，對模型的日回歸系數進行基于估計誤差方差的動態調整是提高模型擬合效果和預測能力的關鍵。從模型的擬合結果來看，在HARQ(F)、HARQ(F)-CJ和LHARQ(F)-CJ模型，日回歸系數的變動部分系數顯著為負，而周、月回歸系數的變動部分系數不顯著。從模型的樣本外預測結果來說，僅對日回歸系數進行調整的HARQ、HARQ-CJ、LHARQ-CJ模型的損失函數較低，向前一期的波動率預測能力較強。

第三，中國股市波動存在跳躍行為及持續的杠桿效應，波動的連續成分和跳躍成分、以及波動的杠桿效應對未來波動率都有一定的解釋作用。LHARQ(F)-CJ模型不僅能夠刻畫估計誤差的異方差特點，還考慮到了波動率的跳躍行為及杠桿效應對預測的作用。在對上證綜合指數波動率的擬合和預測上，與現有模型相比表現較優。本文的研究結論可以應用在股市波動測量、金融資產定價和風險管理等領域。

[1] Andersen T G,Bollerslev T.Deutsche Mark-Dollar Volatility: Intraday activity patterns,macroeconomic announcements and longer run dependencies[J].Journal of Finance,1998,53(1): 219-265.

[2] Andersen T G,Bollerslev T,Diebold F X,et al.Modeling and forecasting realized volatility[J].Econometrica,2003,71(2): 579-625.

[3] Corsi F.A simple approximate long-memory model of realized volatility[J].Journal of Financial Econometrics,2009,7(2): 174-196.

[4] 魏宇.滬深300股指期貨的波動率預測模型研究[J].管理科學學報，2010,13(2): 66-76.

[5] Andersen T G,Bollerslev T,Diebold F X.Roughing it up: Including jump components in the measurement,modeling,and forecasting of return volatility[J].Review of Economics and Statistics,2007,89(4): 701-720.

[6] Bollerslev T,Kretschmer U,Pigorsch C,et al.A discrete-time model for daily S&P500 returns and realized variations: Jumps and leverage effects[J].Journal of Econometrics,2009,150(2): 151-166.

[7] Corsi F,Reno R.HAR volatility modeling with heterogeneous leverage and jumps[R].Working Paper,University of Lugano,2009b.

[8] 陳浪南，楊科.中國股市高頻波動率的特征、預測模型以及預測精度比較[J].系統工程理論與實踐， 2013,33(2): 296-307.

[9] 孫潔.考慮跳躍和隔夜波動的中國股票市場波動率建模與預測[J].中國管理科學，2014,22(6): 114-124.

[10] Asai M,Mcaleer M,Medeiros M C.Modelling and forecasting noisy realized volatility[J].Computational Statistics and Data Analysis,2012,56 (1): 217-230.

[11] Dobrev D P,Szerszen P J.The information content of high-frequency data for estimating equity return models and forecasting risk[R].Working Paper,Federal Reserve Board,2010.

[12] Jacod J,Li Yingying,Mykland P A,et al.Microstructure noise in the continuous case: the preaveraging approach[J].Stochastic Processes and Their Applications.2009,119(7): 2249-2276.

[13] Andersen T G,Bollerslev T,Meddahi N.Realized volatility forecasting and market microstructure noise[J].Journal of Econometrics,2011,160 (1): 220-234.

[14] Bandi F M,Russell J R.Separating microstructure noise from volatility[J].Journal of Financial Economics,2006,79 (3): 655-692.

[15] 唐勇.考慮微觀結構噪聲與跳躍影響的波動建模[J].數學的實踐與認識，2012,42(5): 25-36.

[16] 馬丹，尹優平.噪聲、跳躍與高頻價格波動——基于門限預平均實現波動的分析[J].金融研究，2012,382(4): 124-139.

[17] Barndor-Nielsen O E,Shephard N.Impact of jumps on returns and realized variances: Econometric analysis of time-deformed levy process[J].Journal of Econometrics,2006,131(1): 217-252.

Abstract： As high-frequency data is widely used in forecasting stock volatility,we propose a new family of easy-to-implement models based on realized volatility,which is constructed from the summation of the squared high-frequency intraday returns.In this paper,the estimation error of the realized volatility is assumed to obey the assumption of heteroscedasticity.When modeling the volatility of stock market,we set the autoregressive coefficients of the model according to the change of estimation errors’ variances and get HARQ (F) model.In the meantime,we propose HARQ (F)-CJ model and LHARQ (F)-CJ model in combination with the jump behavior and leverage effect of Chinese stock market volatility to improve the fitness and predictive power of the realized volatility model.We suppose,the larger the estimation error’s variance of the realized volatility or the continuous component in the current period,the worse its interpretation of the latent volatility in the future ,and the smaller the corresponding coefficient is.Through an empirical study on the high-frequency data of the Shanghai Composite Index from December 31st,2015 to January 2nd,2001,we find that based on the assumption of heteroscedasticity in the estimation errors,dynamic coefficients can improve the fitness and the predictive power of the realized volatility model.Above all,the dynamic adjustment of daily regression coefficient based on estimation error variance is the key to improve the fitness and predictive power of the model.The LHARQ-CJ model in combination with both the jump behavior and the leverage effect of the Chinese stock market is considered to show the best performance in all related models.Finally,this research has made its contribution in modeling and forecasting Chinese stock volatility with dynamic estimation errors and dynamic autoregressive coefficients.

Keywords： realized volatility;dynamic estimation errors;high-frequency data;jump behavior;leverage effect

Modeling and Forecasting Volatility of Chinese Stock Market Based on Dynamic Estimation Errors

SONGYa-qiong1,WANGXin-jun2

(1.Party School of Taian Committee of C.P.C.Taian 271000,China;2.School of Economics,Shandong University,Jinan 250100,China)

F830.91

A

1003-207(2017)09-0019-09

10.16381/j.cnki.issn1003-207x.2017.09.003

2016-05-31；

2016-09-26

教育部人文社科規劃基金項目(13YJAZH091)

宋亞瓊(1988-)，女(漢族)，山東泰安人，中共泰安市委黨校，講師，經濟學博士，研究方向：計量經濟學模型及其應用、金融計量分析,E-mail:songyaqiong1988@126.com.