組合指數在環境混合物聯合毒性研究中的初步應用

李愷，劉樹深,*，屈銳

1. 長江水環境教育部重點實驗室，上海 2000922. 同濟大學環境科學與工程學院，上海 200092

組合指數在環境混合物聯合毒性研究中的初步應用

李愷1,2，劉樹深1,2,*，屈銳1,2

1. 長江水環境教育部重點實驗室，上海 2000922. 同濟大學環境科學與工程學院，上海 200092

化學品在實際環境中總是以組分繁雜多變的混合物形式存在，其混合物的毒性評估與預測一直是環境毒理學研究重點。在環境毒理學領域，濃度加和(concentration addition, CA)及獨立作用(independent action, IA)是評估與預測化學混合物聯合毒性的經典模型，一般認為CA適用于作用模式相似的混合物體系而IA適用于作用模式相異的混合物體系，但如何使用CA與IA一直存在爭議。組合指數(combination index, CI)是在半數效應方程基礎上發展起來的不依賴于作用模式的用于混合物聯合毒性評估的混合物毒性指數，具有堅實的理論基礎，不僅能定性地評估毒理學相互作用，也能定量地評估相互作用的大小，已在藥物組合研究中得以廣泛應用，近年來已引起環境毒理學研究者興趣。本文就組合指數及藥物組合應用、進入環境毒理學領域、與CA及IA的關系、存在的問題等幾個方面進行評述，以期推進CI在化學混合物毒性評估與預測領域中的應用。

組合指數；藥物組合；聯合毒性；UD-Ray；置信區間

Received14 January 2017accepted2 March 2017

Abstract: Various chemicals always exist as complex mixtures in real environment. The assessment and prediction of toxicity for chemical mixtures has been the research focus in environmental toxicology. The concentration addition (CA) and independent action (IA) are the classic additive reference models for the toxicity assessment and prediction of chemical mixture. It is generally recognized that the IA model is suitable to estimate the toxicities of the mixtures of the components showing dissimilar modes of actions (MOA), and the CA to the mixtures consisting of the chemicals with similar MOA. But how to correctly use CA and IA has been controversial for a long time. Combination index (CI) has solid theory basis for the reason that it is based on the median-effect equation and independent of the toxic MOA, and CI could qualitatively determine the toxicological interactions and quantitatively evaluate the degree of interaction. The CI has been widely used in drug combination. In recent years, CI is increasingly attracting interests of environmental toxicology researchers. In this review, the fundamental concepts and its application to drug combination and environmental toxicology field, the differences between CI and CA (or IA), and the existing problems are summarized, aiming to propel the applications of CI in mixture toxicity assessment and prediction.

Keywords: combination index; drug combination; combined toxicity; UD-Ray; confidence intervals

由不同來源及不同種類化學品組成的化學混合物普遍存在于實際環境體系中，產生的累積與毒性相互作用具有潛在的生態環境與健康風險[1-2]。利用單個化學組分的濃度-效應信息評估或預測不同濃度組成混合物的毒性效應，是目前化學混合物毒性研究的流行方法[3]。

目前，廣泛應用的評估混合物聯合毒性的加和模型主要是效應相加(effect summation, ES)、濃度加和(concentration addition, CA)和獨立作用(independent action, IA)模型。由于ES模型無法解釋“虛擬組合”現象[4]以及將“無中生有”(something from nothing)現象解釋為潛在協同作用[2]，因而逐漸淘汰。

一般認為，CA模型適用于具有相似作用模式的混合物體系，而IA模型則適用于具有相異作用模式的混合物體系[1,5-7]。然而，這2種方法也存在不足，其一，不能直觀定量地表征混合物毒性相互作用的強度；其二，由于很多物質作用模式尚未可知以及如何選擇相異標準也是目前無法解決的難題，因而無法正確選擇CA或IA[8-9]。Chou等[10-14]通過多年的理論研究與實驗驗證，提出了基于半數效應方程但不依賴于作用模式的組合指數(combination index, CI)來評估混合物毒性相互作用，并已廣泛地應用于藥物組合研究[15-17]。近年來開始引起環境科學工作者的關注[18-22]。不同于CA和IA，CI既能定性地評估化學混合物毒性的相互作用，也能定量地表征其相互作用的大小。本文將對CI的提出及應用進行回顧性評述，并且思考CI方法的優化策略，以期推進其在環境毒理學領域的發展。

1 組合指數與藥物組合應用(Combination index and application of drug combination)

自1960年代以來，Chou基于質量作用原理推導了近300個方程，發現藥物(drug)劑量-效應關系符合類似規律[12,23-24]，這些方程可歸納統一為一個稱為半數效應方程(median effect equation, MEE)的形式[25]：

(1)

其中D是藥物濃度；fa是濃度D時的效應，fu= 1 - fa；Dm是半數效應濃度；m是表征劑量-效應關系形狀的系數，m = 1、>1或<1分別表示雙曲線、S型曲線或扁平S型曲線。

經過簡單變換，MEE可以線性化為：

(2)

從線性化的MEE可知，如果藥物濃度D與效應fa都足夠精確，那么已知任意2組D與fa數據即可通過求解二元一次方程組獲得m和Dm值，即確定劑量-效應曲線方程，進而求得已知效應(fa)下的濃度(D)或已知濃度下的效應。MEE已廣泛應用于藥理學研究[26-32]。

1981年在半數效應方程研究取得成功的基礎上，Chou提出了不依賴于組分作用模式(mode of action, MOA)的用于評估藥物聯合效應的組合指數方法。設混合物由n個組分組成，那么在混合物效應為x%時的該混合物的組合指數(CI)x定義如下：

(3)

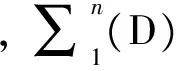
CI已被藥理學工作者廣泛應用于藥物組合研究中[33-38]。例如CI曾被用來研究植物吲哚和異硫氰酸鹽對HepG2-C8細胞的相互作用[1]，研究從植物中來的酚酸對肝毒性的影響作用[39]。Gonzálezpleiter等[40]以魚腥藻和綠藻為測試生物，測定了羥氨芐青霉素、紅霉素、左氧氟沙星、諾氟沙星和四環素單獨存在及混合物毒性，采用CI方法來分析混合物，大部分混合物都出現了協同，并對比了CI、CA和IA這3種方法來預測混合物的毒性，認為CI能更準確地預測加和效應的偏離。Santillo等[41]應用CI研究了單胺氧化酶抑制類藥物(MAO)混合物對PC12、MH1C1和HuH-7細胞的毒性，發現均為加和作用。del Rio等[42]用CI來評估組胺和酪胺2種生物胺對腸細胞的聯合毒性，實時分析研究顯示兩者有明顯的協同效應。Smith等[43]總結了用CI對自然共生的真菌毒素聯合毒性所進行的研究，認為拮抗、加和或協同作用依賴于其種類、細胞模型、混合體系，并不一定是時間或劑量依賴。在藥物組合研究方面，Berenguer-Daize等[30]用CI評估對依維霉素、SN38及替莫唑胺3種抗腫瘤藥物的不同組合下的聯合作用。Chen等[44]用CI來優化2種藥物對腫瘤細胞化療效果的最佳混合比例，得出Nav∶DOX質量比為2∶1時最優。

在CI得到學界認可的同時，為了考察多個組分構成的多元混合物中各個組分之間的各種相互作用情況，Chou[45]創造性地提出了劑量減少指數(dose reduction index, DRI)，來表征某組分在混合物引起混合物效應的濃度比單獨存在時產生效應的濃度減少的倍數。DRI是度量在有協同效應的混合物體系中，在給定的效應水平下，每一種藥物與其單獨使用時的劑量相比可以減少多少倍。在臨床條件下，DRI至關重要，劑量減少使得對宿主的毒性減少但治療效率保持穩定(或不變)。與DRI一并創造性提出的，還有多邊形等效線圖的概念和構建方法，其形象地描述多元混合物中兩兩組分之間的相互作用及程度[46]。多邊形的概念來自于實際應用而非數學推導[45]。然而，要系統、簡潔地表達全部的組合及對應體系在某一混合比下的相互作用是一件非常繁復的事情。例如，即使5個藥物兩兩組合就多達10種。多邊形等效線圖則可簡單形象地在視覺上表現出這一系列的總體結果。在藥物組合研究中，CI結合DRI與多邊形等效線圖的應用，可以更直觀有效地表征不同藥物組合所得效果，以便比較并篩選出最佳藥物組合。

2 進入環境毒理學領域(Into environmental toxicology field)

藥物及化學品的使用會使它們最終流向實際環境。而實際環境體系中混合暴露是一種普遍規律。因此，CI在藥物組合及藥理學領域的應用研究也可為環境混合物聯合毒性方面的研究提供理論依據及技術支撐，一脈相承。這使得CI在環境科學領域的應用極具現實意義。

近年來，CI已經引起環境科學工作者的關注，有學者用CI評估次氯酸鈉(NaOCl)、EDTA和氯己定(CHX)等3種根管沖洗液兩兩間二元混合物對MRC5細胞的聯合毒性，結果顯示單個物質對細胞呈時間依賴毒性特征，且NaOCl/CHX與NaOCl/EDTA二元混合物為拮抗作用，EDTA/CHX二元混合物呈現由加和轉向拮抗的趨勢[47]。Yusoff等[48]用CI評估SG-SBR與HG-SBR中苯酚的抑制效應，并以m值來判定擬合曲線的形狀，其結果為m<1，為平坦的S型，擬合數據顯示抑制效應與苯酚濃度呈正相關，即微生物的抑制效應隨苯酚濃度的增加而增加。Mater等[49]評估了醫藥廢水及地表水中的環丙沙星、三苯氧胺和環磷酰胺的生態風險，指出觀測到的協同及拮抗作用必須考察低濃度及不同的時間暴露混合物的生態毒性效應。Gonzálezpleiter等[40]研究了5種抗生素及其混合物對水生光合生物的毒性，用CI、CA和IA這3個模型評估了混合物的相互作用，認為CI能更準確地預測。Ma等[50]應用CI對12種在中國飲食中常見的農藥及其混合物對肝癌細胞的聯合毒性進行了評估，二元混合物在低濃度呈拮抗、中等濃度呈加和、高濃度為協同，三元混合物有多種相互作用現象，四元、五元及更多元混合物主要呈拮抗作用，而對于2個單個物質、1個二元混合物、3個多元混合物呈現顯著的時間或劑量依賴毒性，其認為產生細胞毒性可能歸因于這些農藥會潛在引起細胞促氧化作用或誘導細胞凋亡。

CI不僅僅在水環境等相關研究中有所應用，還更多地聚焦于多種環境介質混合污染物的毒性相互作用評價[18,20,40]。有學者[51]運用CI法研究2個殺蟲劑，高效氯氟氰菊酯和吡蟲啉，與重金屬鎘對蚯蚓的相互作用，發現在人工濾土試驗中，高效氯氟氰菊酯和鎘在低效應時有輕微協同，在濃度高于某值時轉為輕微拮抗，含有吡蟲啉的二元混合物則呈現拮抗。含有吡蟲啉的三元混合物也對蚯蚓有拮抗。Feng等[52]用CI評估了農藥-離子液體-取代酚六元混合物體系對秀麗線蟲的時間毒性，發現該混合物體系產生了時間協同作用。Tang等[22]用CI評估重金屬-農藥-離子液體三元混合物體系的聯合毒性，發現混合物中草甘膦的濃度分數增加時，其毒性呈現向加和甚至拮抗變化的趨勢。Liu等[21]用CI評估了不含J型組分混合物的毒性相互作用，表明除少數混合物射線在高效應水平疑似存在協同或拮抗外，其余所有混合物均為加和作用。Wang等[51]運用CI評價了除草劑、殺蟲劑和重金屬三元混合物體系的聯合毒性并顯示出協同作用。Chen等[53]運用CI評價了四元、五元、六元、七元及八元混合物體系的聯合毒性，并將CI與CA和IA進行對比。

區別于藥物組合與藥理學領域，環境混合物聯合毒性的研究對進行風險評價、改進環境標準和環境容量都有很強的推動作用和現實意義。環境混合物的復雜性使得研究人員不能只局限于在固定濃度比(或等效應濃度比)下研究二元混合物，這也是CI在藥物組合與環境混合物方面應用的差異。對于二元混合物的實驗設計，Chou等[54]提出的對角等比率組合設計能大大地減少實驗需要的動物數量(即大大減少所需數據點的數量)，與直接均分射線設計法[55]一樣，優化了固定濃度比射線法(fixed concentration ratio ray, FCRR)。對于多組分混合物，例如三元混合物，Chou[9]推薦對其進行兩兩組合，簡化計算。然而組分越多，即便簡化也會大大增加工作量，還是需要優化實驗設計。

在環境混合物聯合毒性研究中，前文提及的DRI與多邊形等效線圖的應用鮮有問津，但對于研究多組分的環境混合物聯合毒性及對環境生態風險進行評價而言，這2種方法可更加形象地表達關鍵組分對混合物聯合毒性的貢獻及混合物體系相互作用關系，值得拓展與深入研究。

3 與CA及IA的關系(The difference from CA or IA)

半數效應方程與組合指數最獨特也是最重要的特點就是方程的每一項都是比值(方程1、方程3)。因此，對于化學品(或藥物)實體，單位是可以抵消的，從而成為一個無量綱[9]。此特點是它們可以廣泛應用的核心內容，即不依賴于組分作用模式。而前已述及環境中的污染物往往以混合物的形式出現，混合物體系復雜多變，其組分的作用模式難以一一考究，在選擇模型過程中很難統一或者嚴格區分不同的作用模式，因此對CA與IA模型的使用前提一直是眾多科研工作者爭論的焦點之一[7-8,56-58]。而CI避免了這種爭論，就更具理論意義、更加適用于復雜混合污染物的毒性分析。

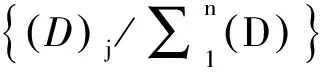
(4)

顯然，當CI = 1時就是濃度加和模型CA的表達式：

(5)

單從數學層面而言，方程5左側值可以看作方程4左側CI值的歸一化處理。需要強調的是，CI、CA或IA所表達的劑量效應關系本質上并不揭示機理。當表達協同(或拮抗)效應時，常常會涉及協同的機理是什么？這是一個很難回答的問題。事實上，我們對藥物及化學品機理知之甚少。這里的一個論點是，所指的機理是什么，是藥理學上的、生物化學的、細胞水平的、分子水平的、化學的、或量子力學水平上？細究機理時，我們還面對一個問題：當受試生物達到作用靶點時，我們實際上不知道其在達到作用靶點前有多少事件發生。這可能是幾個階段或數百個階段。此外，當我們談及2個或多個藥物或化學品的協同或拮抗效應時被認為是相互的。雖然我們知道單個組分在混合物中的劑量或效應貢獻，但我們并不能定量地知道每一個藥物或化學品對所導致觀察到的協同或拮抗效應中機理貢獻的比例[9]。因此，有關CA模型適用于具有相似作用模式的混合物體系，而IA模型則適用于具有相異作用模式的混合物體系的理論基礎并不穩固，還需驗證[57,63]。在選擇評估模型對環境混合物體系進行相互作用評估時，應當將CI、CA或IA作為一個工作模型來使用，將受試生物體看作黑箱，不必關注藥物或化學品對受試生物的作用方式和作用位點。

那么，從數學角度并剔除CI、CA模型建立的理論基礎討論，半數效應方程的作用等同于用于毒性數據非線性擬合的Hill函數或Logit函數或Weibull函數(或其他函數)，區別在于半數效應方程、Logit函數及Weibull函數為兩參數模型，Hill函數為四參數模型。因此，CI與CA本質上并無太多差異，或者說CI就是CA，但CI不僅可直觀地定性表達相互作用，而且可定量地表示毒性相互作用的大小。

回到模型的理論基礎，值得一提的是組合指數基于質量作用定律，半數效應方程的重排或采用它的對數形式可推導出生物醫學科學中的4個主要方程，即對于一階酶動力學(m=1)的Michaelis-Menten方程、用于主要配體占據生物受體的高階Hill方程、用于配體-受體結合及解離的Scatchard方程，以及用于pH離子化的Henderson-Hasselbalch方程[9]。這樣，共用相同數學形式的方程可具有不同的物理化學意義，同時半數效應方程的兩邊是比值，這樣等式中左右兩側的值是沒有單位的，這比CA及IA模型的理論基礎更為扎實，可完全避免作用模式異同的爭論。

4 組合指數與混合物設計的優化策略(Optimization)

環境混合物聯合毒性研究是一項極具挑戰的課題，在人力、物力、財力條件有限的情況下，如何更有效地對環境混合物聯合毒性進行評估，同時兼顧實際環境體系的復雜性，值得研究者深思。而從混合物毒性相互作用的實驗設計開始，不失為一個好的開端。

在此，我們有必要重申混合物體系與混合物射線的概念：具有明確化合物組分的一系列混合物稱之為混合物體系，如二元混合物、三元混合物；混合物體系中的一系列具有固定濃度分數的混合物稱之為混合物射線。每一個混合物體系中均包含了無數個不同固定比的混合物射線。只有從固定的混合物射線形成的劑量-效應曲線所得毒性大小才能與單個物質的毒性作比較，而非一個混合物體系。

實際環境混合物體系的復雜多變使得要全面研究所有混合物是不可能的，所以混合物的濃度組成或濃度配比必須進行優化設計。藥物組合研究多為組分較少，毒性研究比較普遍，其設計方法相對完善的二元混合物。對于多元混合物的設計，環境科學領域的學者多只用固定濃度比射線法與等效應濃度比射線法(equivalent effect concentration ratio ray, EECR)，但兩者都只是設計了一條混合物射線，而非系統完整的混合物體系，且EECR法是固定濃度比為某特定效應濃度(如EC50)的FCRR法，是FCRR法的一種特例。這2種方法設計的混合物組分濃度比的分布范圍較窄，不能反映混合物組分在整個多維濃度空間內不同濃度分數的混合，也不能代表環境實體的濃度分布，即使再多的等效應濃度比混合物，也不可能完全探測到混合物的整體濃度空間。另外，雖有學者認為等毒性濃度比射線可以最大化估計毒性效應[64]，但此論斷并不準確，因為并未考察全部的混合物濃度空間。混合物實驗設計與混合物聯合毒性評價密不可分，模型評價得到的混合物相互作用往往具有組成依賴性。例如在研究二元重金屬對Tympanotonus fuscatus毒性時發現，鋅銅比為1∶4時，呈強拮抗，而鋅銅等毒性比時則為加和[65]。Cedergreen等[66]指出氯丙酸與特丁津的二元混合物對浮游植物Lemna minor的聯合毒性與組成成分濃度有關，混合物中氯丙酸所占比例越高則拮抗作用越大。

為了有效合理地探索整個混合物濃度空間的毒性變化規律，劉樹深教授課題組創造性地將我國數學家王元和方開泰[67]提出的一種新的優化實驗設計——均勻設計思想引入混合物聯合毒性研究之中，提出了均勻設計射線法(uniform design ray, UD-Ray)[68]。以3組分各5個濃度的實驗體系為例，比較析因設計(factorial design, FD)、正交設計(orthogonal design, OD)和均勻設計(uniform design, UD)3種優化試驗設計方法所選擇的三維濃度空間中有代表性的實驗點，結果如圖1所示。對于析因設計，當考察3個因素各5個水平時所需要的實驗數為35= 125次(不考慮重復)，而正交實驗雖然只需要25次實驗，僅為析因設計實驗數的1/5，但實驗數仍是比較多的。顯然，均勻設計所需代表性實驗最少，僅需5次實驗。

基于此，等效應濃度比或固定濃度比并不能很好地表達一個混合物體系的毒性，更難以模擬實際環境中化學混合物的多種濃度變化。對混合物毒性的評估與預測應當更多地應用UD-Ray進行混合物聯合毒性研究的實驗設計。該方法可使實驗點在濃度范圍內均勻散布的優化實驗設計方法，具有能充分代表混合物中的各種濃度變化的樣本校正集，能

有效地選擇有代表性的實驗點，能更好地實現不同組成混合物聯合毒性的真正預測。正因其獨到的優勢，已被多次應用在混合物毒性實驗中[3, 21-22,50,69]。

除卻混合物設計優化方面的考量，另個一直注意的問題是目前所有關于CI應用的文獻都把它作為一個準確的參考標準來實施混合物毒性相互作用評價。事實上，所有毒性實驗都存在實驗誤差，不同毒物或污染物具有不同的劑量-效應特征(如短長期毒性差異與含無效應組分等)，劑量-效應曲線擬合也存在擬合誤差，這些都會影響CI指數的不確定度。因此，必須考慮CI指數的置信區間。Liu等[21]綜合考慮實驗誤差、不同劑量-效應特征與擬合誤差對CI的影響，構建了基于觀測置信區間的CI指數(combination index based on the confidence intervals, CI-Int)，并將其應用在二元及多元混合物相互作用研究中，使其能夠更加準確地評估混合物毒性。

組合指數結合UD-Ray及置信區間，對于在環境混合物聯合毒性研究方面的應用必將是協同效應，正所謂寶鞍配良駒，寶玉配佳人。

5 融會貫通助推毒理學發展(Development by correct understanding)

對組合指數開創性的拓展，使得其在環境混合物聯合毒性研究領域的應用更趨完善，類似的拓展同樣可以推廣至藥物組合及藥理學的研究中。公式的推導與拓展在使用層面上，更容易被學者接受和理解，但這并不意味著能用好對應的評估模型。

Liu等[70]在評論“The synergistic toxicity of the multi-chemical mixtures: Implications for risk assessment in the terrestrial environment”[53]一文時談及就CI而言，并不能預測混合物聯合毒性，只能評估混合物相互作用。在此，有必要對CA與CI模型所涉及的ECx,mix的數學推導再次討論說明。

對于方程推導，回顧方程5，指定效應時，應用CA模型預測混合物濃度的公式為：

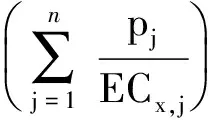
(6)

其中ECx,mix是CA預測的混合物產生x%效應時的濃度。Chen等[53]論文中依據CA的推導，在CI方程的基礎上推導了一個預測方程：

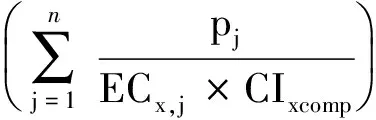
(7)

其中CIxcomp是混合物產生x%效應時由計算得到的CI值。對于CA模型，方程6根據單個組分的劑量-效應曲線以及其在混合物中的比例計算。而對于方程7，首先需要計算得到CI值。簡單的講，方程6僅有一個變量，而方程7則為一個變量一個因變量。根據方程3，在給定效應下計算CI值必須知道混合物的總濃度，即得到ECx,mix必須先獲得混合物的劑量-效應曲線，從而擬合得到對應的濃度，這違背了“預測”一詞的本意，顯得本末倒置。值得注意的是，方程6與方程7有本質的區別，方程6在計算ECx,mix值僅需依據效應濃度ECx,j以及其在混合物射線中混合比pj，無關于混合物射線的劑量-效應曲線。

同樣的理解偏差，也存在其他一些學者的研究成果中。Gonzálezpleiter等[40]用CI、CA、IA這3個模型評估了5種抗生素混合物對水生光合生物聯合毒性，認為CI能更準確地預測。Chen等[71]在人工土、濾紙上研究了2種除草劑(去草胺與阿特拉津)和一種殺蟲劑(高效氯氟氰菊酯)，對陸地非目標生物蚯蚓的單個及聯合毒性，并比較CI與傳統模型CA與IA，認為CI可以在生態風險評估中準確地預測混合物毒性。Trombini等[72]分別用CA、IA及CI預測了撲熱息痛、卡馬西平、雙氯芬酸及布洛芬4種新型環境污染物的混合物對無節幼蟲的毒性，認為CA和IA不能很好地預測藥物混合物毒性，而CI可以。Chen等、Trombini等及Gonzálezpleiter等并未正確理解CI模型及“預測”這一概念。在此，我們強調對評估模型的透徹理解及正確使用，是進行環境混合物聯合毒性研究的重要前提之一。

[1] Faust M, Altenburger R, Backhaus T, et al. Predicting the joint algal toxicity of multi-component S-triazine mixtures at low-effect concentrations of individual toxicants [J]. Aquatic Toxicology, 2001, 56(1): 13-32

[2] Silva E, Rajapakse N, Kortenkamp A. Something from "nothing" - Eight weak estrogenic chemicals combined at concentrations below NOECs produce significant mixture effects [J]. Environmental Science & Technology, 2002, 36(8): 1751-1756

[3] 王猛超, 劉樹深, 陳浮. 拓展濃度加和模型預測三種三嗪類除草劑混合物的時間依賴毒性[J]. 化學學報, 2014(1): 56-60

Wang M-C, Liu S-S, Chen F. Predicting the time-dependent toxicities of three triazine herbicide mixtures to V. qinghaiensis sp. Q67 using the extended concentration addition model [J]. Chimica Sinica, 2014(1): 56-60 (in Chinese)

[4] 劉樹深, 劉紅玲, 陳浮. 濃度加和模型在化學混合物毒性評估中的應用[J]. 化學學報, 2013(10): 1335-1340

Liu S-S, Liu H-L, Chen F. Application of the concentration addition model in the assessment of chemical mixture toxicity [J]. Chimica Sinica, 2013(10): 1335-1340 (in Chinese)

[5] Altenburger R, Backhaus T, Boedeker W, et al. Predictability of the toxicity of multiple chemical mixtures to Vibrio fischeri: Mixtures composed of similarly acting chemicals [J]. Environmental Toxicology and Chemistry, 2000, 19(9): 2341-2347

[6] Backhaus T, Altenburger R, Boedeker W, et al. Predictability of the toxicity of a multiple mixture of dissimilarly acting chemicals to Vibrio fischeri [J]. Environmental Toxicology and Chemistry, 2000, 19(9): 2348-2356

[7] Spurgeon D J, Jones O A H, Dorne J-L C M, et al. Systems toxicology approaches for understanding the joint effects of environmental chemical mixtures [J]. Science of the Total Environment, 2010, 408(18): 3725-3734

[8] Cleuvers M. Aquatic ecotoxicity of pharmaceuticals including the assessment of combination effects [J]. Toxicology Letters, 2003, 142(3): 185-194

[9] Chou T-C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies [J]. Pharmacological Reviews, 2006, 58(3): 621-681

[10] Chou T-C. Preclinical versus clinical drug combination studies [J]. Leukemia & Lymphoma, 2008, 49(11): 2059-2080

[11] Chou T-C. Drug combination studies and their synergy quantification using the Chou-Talalay Method [J]. Cancer Research, 2010, 70(2): 440-446

[12] Chou T-C. The mass-action law based algorithms for quantitative econo-green bio-research [J]. Integrative Biology, 2011, 3(5): 548-559

[13] Reis M A, Ahmed O B, Spengler G, et al. Jatrophane diterpenes and cancer multidrug resistance-ABCB1 efflux modulation and selective cell death induction [J]. Phytomedicine, 2016, 23(9): 968-978

[14] D'Ors A, Cortés A A, Sánchez-Fortún A, et al. Interference of heavy metals on the photosynthetic response from a Cr(VI)-resistant dictyosphaerium chlorelloides strain [J]. Ecotoxicology, 2016, 25(1): 15-21

[15] Yamamoto Y, Hyodo I, Takigahira M, et al. Effect of combined treatment with the epirubicin-incorporating micelles (NC-6300) and 1,2-diaminocyclohexane platinum (II)-incorporating micelles (NC-4016) on a human gastric cancer model [J]. International Journal of Cancer, 2014, 135(1): 214-223

[16] Saw C-L, Cintrón M, Wu T-Y, et al. Pharmacodynamics of dietary phytochemical indoles I3C and DIM: Induction of Nrf2-mediated phase II drug metabolizing and antioxidant genes and synergism with isothiocyanates [J]. Biopharmaceutics & Drug Disposition, 2011, 32(5): 289-300

[17] Cazzola M, Calzetta L, Ora J, et al. Searching for the synergistic effect between aclidinium and formoterol: From bench to bedside [J]. Respiratory Medicine, 2015, 109(10): 1305-1311

[18] Rodea-Palomares I, Petre A L, Boltes K, et al. Application of the combination index (CI)-isobologram equation to study the toxicological interactions of lipid regulators in two aquatic bioluminescent organisms [J]. Water Research, 2010, 44(2): 427-438

[19] Gonzalez-Sanchez I, Lira-Rocha A, Navarrete A, et al. Synergistic anticancer activity of thiazolo 5,4-b quinoline derivative D3CLP in combination with cisplatin in human cervical cancer cells [J]. Anticancer Research, 2012, 32(12): 5159-5165

[20] Rodea-Palomares I, Leganes F, Rosal R, et al. Toxicological interactions of perfluorooctane sulfonic acid (PFOS) and perfluorooctanoic acid (PFOA) with selected pollutants [J]. Journal of Hazardous Materials, 2012, 201: 209-218

[21] Liu L, Liu S-S, Yu M, et al. Application of the combination index integrated with confidence intervals to study the toxicological interactions of antibiotics and pesticides in Vibrio qinghaiensis sp.-Q67 [J]. Environmental Toxicology and Pharmacology, 2015, 39(1): 447-456

[22] Tang H-X, Liu S-S, Li K, et al. Combining the uniform design-based ray procedure with combination index to investigate synergistic lethal toxicities of ternary mixtures on Caenorhabditis elegans [J]. Analytical Methods, 2016, 8(22): 4466-4472

[23] Chou T-C. Comparison of mass-action law with power law, probit law and logit law in dose-effect analyses [J]. Pharmacologist, 1977, 19(2): 165

[24] Chou T-C, Talalay P. Generalized equations for the analysis of inhibitions of Michaelis-Menten and higher-order kinetic systems with 2 or more mutually exclusive and non-exclusive inhibitors [J]. European Journal of Biochemistry, 1981, 115(1): 207-216

[25] Chou T-C. Derivation and properties of Michaelis-Menten type and hill type equations for reference ligands [J]. Journal of Theoretical Biology, 1976, 59(2): 253-276

[26] Chang T-T, Chou T-C. Rational approach to the clinical protocol design for drug combinations: A review [J]. Acta Paediatrica Taiwanica, 2000, 41(6): 294-302

[27] Bence A K, Adams V R, Crooks P A. L-Canavanine as a radiosensitization agent for human pancreatic cancer cells [J]. Molecular and Cellular Biochemistry, 2003, 244(1): 37-43

[28] Xu M-J, Alberts D S. Potentiation of platinum analog cytotoxicity by hyperthermia [J]. Cancer Chemotherapy and Pharmacology, 1988, 21(3): 191-196

[29] Pimenta F, Abreu A C, Simoes L C, et al. What should be considered in the treatment of bacterial infections by multi-drug therapies: A mathematical perspective? [J]. Drug Resistance Updates, 2014, 17(3): 51-63

[30] Berenguer-Daize C, Astorgues-Xerri L, Odore E, et al. OTX015 (MK-8628), a novel BET inhibitor, displays in vitro and in vivo antitumor effects alone and in combination with conventional therapies in glioblastoma models [J]. International Journal of Cancer, 2016, 139(9): 2047-2055

[31] Zimmer A, Katzir I, Dekel E, et al. Prediction of multidimensional drug dose responses based on measurements of drug pairs [J]. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(37): 10442-10447

[32] Zhou X, Seto S W, Chang D, et al. Synergistic effects of Chinese herbal medicine: A comprehensive review of methodology and current research [J]. Frontiers in Pharmacology, 2016, 7: 201

[33] Tanamatayarat P, Sotanaphun U, Poobrasert O. Thai plants from Doi Tung: Brine shrimp lethality, antioxidative activity and combination effect with L-ascorbic acid [J]. Natural Product Research, 2012, 26(10): 919-925

[34] Du G-S, Pan J-Z, Zhao S-P, et al. Cell-based drug combination screening with a microfluidic droplet array system [J]. Analytical Chemistry, 2013, 85(14): 6740-6747

[35] Zhu Y, Zhang Y-X, Cai L-F, et al. Sequential operation droplet array: An automated microfluidic platform for picoliter-scale liquid handling, analysis, and screening [J]. Analytical Chemistry, 2013, 85(14): 6723-6731

[36] Chen T, Gu J, Zhang X, et al. System-level study on synergism and antagonism of active ingredients in traditional Chinese medicine by using molecular imprinting technology [J]. Scientific Reports, 2014, 4: 7159

[37] Jiang C, Wu Z-Q, Liu L, et al. Synergy of herbal ingredients combination against Dactylogyrus spp. in an infected goldfish model for monogenean management [J]. Aquaculture, 2014, 433: 115-118

[39] Liu Y, Flynn T J, Ferguson M S, et al. Use of the combination index to determine interactions between plant-derived phenolic acids on hepatotoxicity endpoints in human and rat hepatoma cells [J]. Phytomedicine, 2013, 20(5): 461-468

[40] Gonzálezpleiter M, Gonzalo S, Rodea-Palomares I, et al. Toxicity of five antibiotics and their mixtures towards photosynthetic aquatic organisms: Implications for environmental risk assessment [J]. Water Research, 2013, 47(6): 2050-2064

[41] Santillo M F, Liu Y, Ferguson M, et al. Inhibition of monoamine oxidase (MAO) by beta-carbolines and their interactions in live neuronal (PC12) and liver (HuH-7 and MH1C1) cells [J]. Toxicology in Vitro, 2014, 28(3): 403-410

[42] del Rio B, Redruello B, Linares D M, et al. The dietary biogenic amines tyramine and histamine show synergistic toxicity towards intestinal cells in culture [J]. Food Chemistry, 2017, 218: 249-255

[43] Smith M-C, Madec S, Coton E, et al. Natural co-occurrence of mycotoxins in foods and feeds and their in vitro combined toxicological effects [J]. Toxins, 2016, 8(4): 94

[44] Chen B, Dai W, Mei D, et al. Comprehensively priming the tumor microenvironment by cancer-associated fibroblast-targeted liposomes for combined therapy with cancer cell-targeted chemotherapeutic drug delivery system [J]. Journal of Controlled Release, 2016, 241: 68-80

[45] Chou T-C. Assessment of synergistic and antagonistic effects of chemotherapeutic agents in vitro [J]. Contributions to Gynecology and Obstetrics, 1994, 19: 91-107

[46] Chou T-C, Chou L H. Computerized indexing of drug combinations: Prediction of synergism and antagonism of more than two drugs by polygonogram [J]. Faseb Journal, 1998, 12(4): A143-A143

[47] Vouzara T, Koulaouzidou E, Ziouti F, et al. Combined and independent cytotoxicity of sodium hypochlorite, ethylenediaminetetraacetic acid and chlorhexidine [J]. International Endodontic Journal, 2016, 49(8): 764-773

[48] Yusoff N, Ong S-A, Ho L-N, et al. Evaluation of biodegradation process: Comparative study between suspended and hybrid microorganism growth system in sequencing batch reactor (SBR) for removal of phenol [J]. Biochemical Engineering Journal, 2016, 115: 14-22

[49] Mater N, Geret F, Castillo L, et al. In vitro tests aiding ecological risk assessment of ciprofloxacin, tamoxifen and cyclophosphamide in range of concentrations released in hospital wastewater and surface water [J]. Environment International, 2014, 63: 191-200

[50] Ma M, Chen C, Yang G, et al. Combined cytotoxic effects of pesticide mixtures present in the Chinese diet on human hepatocarcinoma cell line [J]. Chemosphere, 2016, 159: 256-266

[51] Wang Y, Chen C, Qian Y, et al. Ternary toxicological interactions of insecticides, herbicides, and a heavy metal on the earthworm Eisenia fetida [J]. Journal of Hazardous Materials, 2015, 284: 233-240

[52] Feng L, Liu S-S, Li K, et al. The time-dependent synergism of the six-component mixtures of substituted phenols, pesticides and ionic liquids to Caenorhabditis elegans [J]. Journal of Hazardous Materials, 2017, 327: 11-17

[53] Chen C, Wang Y, Qian Y, et al. The synergistic toxicity of the multiple chemical mixtures: Implications for risk assessment in the terrestrial environment [J]. Environment International, 2015, 77: 95-105

[54] Chou T-C, Talalay P. Quantitative-analysis of dose-effect relationships—The combined effects of multiple-drugs or enzyme-inhibitors [J]. Advances in Enzyme Regulation, 1984, 22: 27-55

[55] Dou R-N, Liu S-S, Mo L-Y, et al. A novel direct equipartition ray design (EquRay) procedure for toxicity interaction between ionic liquid and dichlorvos [J]. Environmental Science and Pollution Research, 2011, 18(5): 734-742

[56] Altenburger R, Nendza M, Schuurmann G. Mixture toxicity and its modeling by quantitative structure-activity relationships [J]. Environmental Toxicology and Chemistry, 2003, 22(8): 1900-1915

[57] Baas J, Van Houte B P, Van Gestel C A, et al. Modeling the effects of binary mixtures on survival in time [J]. Environmental Toxicology and Chemistry, 2007, 26(6): 1320-1327

[58] Cedergreen N, Sorensen H, Svendsen C. Can the joint effect of ternary mixtures be predicted from binary mixture toxicity results? [J]. Science of the Total Environment, 2012, 427: 229-237

[59] Backhaus T, Faust M, Scholze M, et al. Joint algal toxicity of phenylurea herbicides is equally predictable by concentration addition and independent action [J]. Environmental Toxicology and Chemistry, 2004, 23(2): 258-264

[60] Howard G J, Schlezinger J J, Hahn M E, et al. Generalized concentration addition predicts joint effects of aryl hydrocarbon receptor agonists with partial agonists and competitive antagonists [J]. Environmental Health Perspectives, 2010, 118(5): 666-672

[61] Baylay A J, Spurgeon D J, Svendsen C, et al. A metabolomics based test of independent action and concentration addition using the earthworm Lumbricus rubellus [J]. Ecotoxicology, 2012, 21(5): 1436-1447

[62] Gregorio V, Chevre N, Junghans M. Critical issues in using the common mixture toxicity models concentration addition or response addition on species sensitivity distributions: A theoretical approach [J]. Environmental Toxicology and Chemistry, 2013, 32(10): 2387-2395

[63] Jonker M J, Svendsen C, Bedaux J J M, et al. Significance testing of synergistic/antagonistic, dose level-dependent, or dose ratio-dependent effects in mixture dose-response analysis [J]. Environmental Toxicology and Chemistry, 2005, 24(10): 2701-2713

[64] Lin Z, Ping Z, Kong D, et al. The ratios of individual chemicals in a mixture determine the degree of joint effect: The climax hypothesis [J]. Archives of Environmental Contamination and Toxicology, 2005, 49(1): 1-8

[65] Otitoloju A A. Evaluation of the joint-action toxicity of binary mixtures of heavy metals against the mangrove periwinkle Tympanotonus fuscatus var radula (L.) [J]. Ecotoxicology and Environmental Safety, 2002, 53(3): 404-415

[66] Cedergreen N, Kudsk P, Mathiassen S K, et al. Reproducibility of binary-mixture toxicity studies [J]. Environmental Toxicology and Chemistry, 2007, 26(1): 149-156

[67] 王元, 方開泰. 關于均勻分布與試驗設計(數論方法)[J]. 科學通報, 1981, 26(2): 65-70

Wang Y, Fang K-T. A note on uniform distribution and experimental design [J]. Chinese Science Bulletin, 1981, 26(2): 485-489 (in Chinese)

[68] Liu S-S, Xiao Q-F, Zhang J, et al. Uniform design ray in the assessment of combined toxicities of multi-component mixtures [J]. Science Bulletin, 2016, 61(1): 52-58

[69] Zhang J, Liu S-S, Yu Z-Y, et al. The time-dependent hormetic effects of 1-alkyl-3-methylimidazolium chloride and their mixtures on Vibrio qinghaiensis sp.-Q67 [J]. Journal of Hazardous Materials, 2013, 258: 70-76

[70] Liu S-S, Li K, Li T, et al. Comments on "The synergistic toxicity of the multi chemical mixtures: Implications for risk assessment in the terrestrial environment" [J]. Environment International, 2016, 94: 396-398

[71] Chen C, Wang Y, Zhao X, et al. Combined toxicity of butachlor, atrazine and lambda-cyhalothrin on the earthworm Eisenia fetida by combination index (CI)-isobologram method [J]. Chemosphere, 2014, 112: 393-401

[72] Trombini C, Hampel M, Blasco J. Evaluation of acute effects of four pharmaceuticals and their mixtures on the copepod Tisbe battagliai [J]. Chemosphere, 2016, 155: 319-328

◆

ApplicationoftheCombinationIndexintheAssessmentofCombinedToxicityofEnvironmentalMixture

Li Kai1,2, Liu Shushen1,2,*, Qu Rui1,2

1. Key Laboratory of Yangtze River Water Environment, Ministry of Education, Shanghai 200092, China2. College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China

10.7524/AJE.1673-5897.20170114001

2017-01-14錄用日期2017-03-02

1673-5897(2017)3-062-10

X171.5

A

劉樹深(1961—)，男，博士，教授，博士生導師。全國優秀博士學位論文獲得者。主要研究方向為化學混合物分析毒理與分子模擬，近年在國內外學術期刊發表論文100余篇，其中SCI收錄80多篇。

國家自然科學基金(21377097，21177097)

李愷(1986-)，男，博士研究生，研究方向為化學混合物毒理學，E-mail: lee2061@163.com；

*通訊作者(Corresponding author)， E-mail: ssliuhl@263.net

李愷, 劉樹深, 屈銳. 組合指數在環境混合物聯合毒性研究中的初步應用[J]. 生態毒理學報，2017, 12(3): 62-71

Li K, Liu S S, Qu R. Application of the combination index in the assessment of combined toxicity of environmental mixture [J]. Asian Journal of Ecotoxicology, 2017, 12(3): 62-71 (in Chinese)