模型預測控制在光伏并網逆變器中的應用
陳寧寧 宋子豪 汪澤州
?
模型預測控制在光伏并網逆變器中的應用
陳寧寧1宋子豪2汪澤州1
(1. 國網浙江海鹽縣供電公司,浙江嘉興 314300;2. 國網江蘇省電力公司職業技能訓練基地,江蘇連云港 222000)
本文基于兩級式三相并網逆變器的數學模型和模型預測控制的基本原理,提出了一種基于模型預測控制的光伏并網逆變器控制方法。該方法以光伏逆變器的一階差分方程為基礎,建立了其預測模型,通過模型預測算法對光伏并網逆變器未來若干個采樣時刻的三相并網電流值進行預測,再根據滾動優化函數進行最優化求解,進而得到最優的控制變量,具有良好的控制性能和較強的魯棒性。詳細介紹了模型預測控制算法的建立和實現過程,在Matlab/Simulink環境下建立了相應的仿真模型。相關仿真結果表明,模型預測控制算法具有動態響應快和魯棒性強的特點,適用于三相光伏并網逆變器的高性能控制。
光伏逆變器;模型預測控制;階躍響應;魯棒性
太陽能是一種清潔、高效和永不衰竭的新能源。近年來隨著光伏發電成本的迅速降低和國家相關政策的推動,光伏并網發電的利用在能源供應中將占據更重要地位。
逆變器是光伏并網發電系統的關鍵部件,主要作用是將光伏陣列輸出的直流電能逆變成與公共電網等電壓、同頻率、同相位的交流電能并入公共電網,其性能的優劣直接關系到系統向電網輸出的電能質量和系統運行的效率[1]。
1 三相并網逆變器的數學模型
典型的三相兩電平光伏并網逆變器的主電路結構如圖1所示。
在d-q同步旋轉坐標系下,三相并網逆變器交流側的數學模型可以表述為[2]

式中,d、q為并網逆變器輸出電壓的d、q軸分量;d、q為并網逆變器輸出電流的d、q軸分量;d、q為電力系統電壓的d、q軸分量;、為交流側電感及其內阻;為電網的同步角頻率;為對時間的求導算子。
2 采用模型預測控制的并網控制策略
2.1 模型預測控制算法
模型預測控制(model predictive control, MPC)是一種通過對系統未來有限時間域內的狀態進行預測進而確定當前控制動作的控制方式,是一種非線性的最優化控制算法。該算法的主要特點是控制效果好、魯棒性強。
模型預測控制系統主要包括系統預測模型、滾動優化算法和反饋校正環節3個部分[3-4],圖2為其結構原理。

圖2 模型預測控制算法的結構框圖
2.2 模型預測控制在并網逆變器控制中的應用
將式(1)按照一階歐拉法離散化,得到并網逆變器電流環的預測模型[5-7],即

式中,
,,,
d(1)、q(1)表示時刻對未來1時刻電流的預測值,d()、q()表示時刻逆變器輸出的電壓值;d()、q()表示時刻電流的采樣值;d()、q()表示時刻電網電壓的采樣值,s為控制系統的采樣周期。
將式(2)中d、q軸之間的耦合分量看做擾動項,進行前饋解耦,同時將電流環的預測模型分為兩部分:與前一周期逆變器輸出的電壓電流相關的部分d1(1)與電網電壓相關的部分d2(1)。
得到電流環的預測模型為
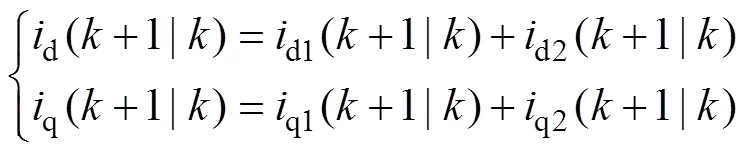
其中
以d軸電流d為例建立預測模型。首先,由d1(1)、q1(1)得到兩個單輸入單輸出(SISO)系統:
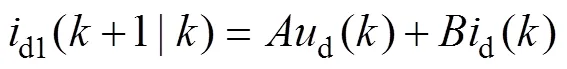
(5)
在實際的控制系統中,控制變量在接下來的個周期都會有著不同的變化量,因此,受控對象的預測值由未考慮控制變量變化的輸出預測值和每個預測周期內控制量變化組成:
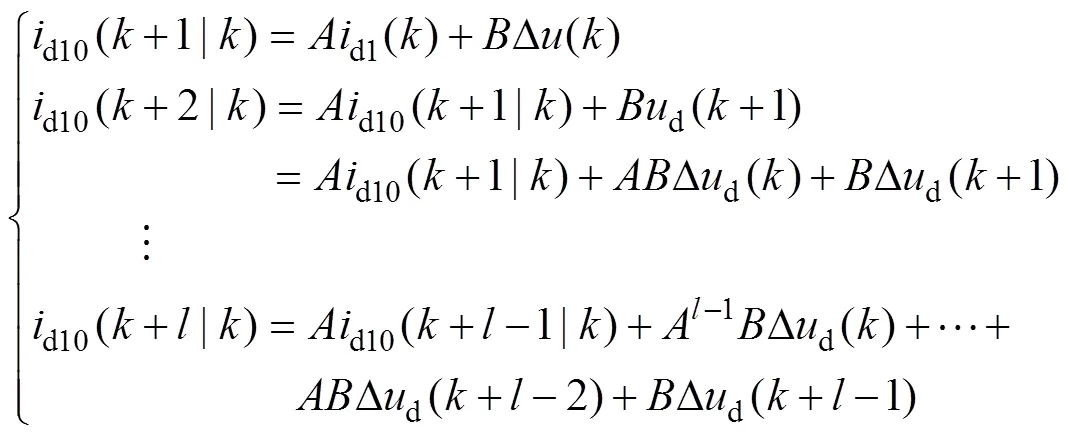
簡寫為式(7)所示的矩陣形式,即
(7)
對于預測模型的第二部分,考慮到并網逆變器的控制周期s較短(數十到數百微秒),認為在未來的個預測周期內,電網電壓的增量保持不變,即

最終得到d軸電流的預測模型為
(9)
實際的受控系統往往存在著模型不精確、采樣誤差及外部因素干擾等多種問題,造成預測模型無法與實際受控對象完全一致,使得并網逆變器輸出電流的預測值與實際值之間存在誤差:
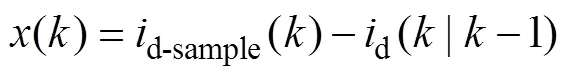
(11)
通過修正后的預測值,系統成為了一個閉環的負反饋系統,從而確保了系統預測值的準確性,并使得系統的魯棒性更強。
本文中MPC算法與傳統的優化控制算法相類似,將二次型目標函數值最小作為對系統進行優化的目標。設受控對象在時刻以后的個預測周期內進行優化,系統的控制目標是實現預測輸出值p()與參考值d_ref()的一致。同時,為保持系統運行的穩定性,控制變量的增量值變化不應過于劇烈。二次型優化目標函數可表示如下:

式中,、r分別為加權系數,是控制算法對跟蹤誤差及控制量增量的抑制。d_ref()是給定的變量期望值,p()是預測的輸出值,和分別是優化時域和控制時域的周期數。表示為如下的矩陣形式:
(13)
式中,R()為參考值矩陣;P()為預測輸出值矩陣,為控制量增量矩陣,為誤差權系數矩陣,=diag(1,…,),為控制權系數矩陣= diag(1,…,r)。
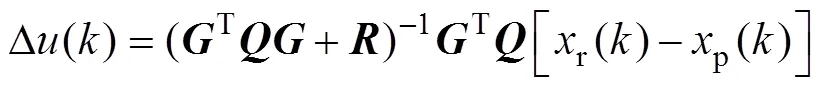
采用所提出的模型預測控制方法,得到改進的三相并網逆變器控制算法框圖如圖3所示。
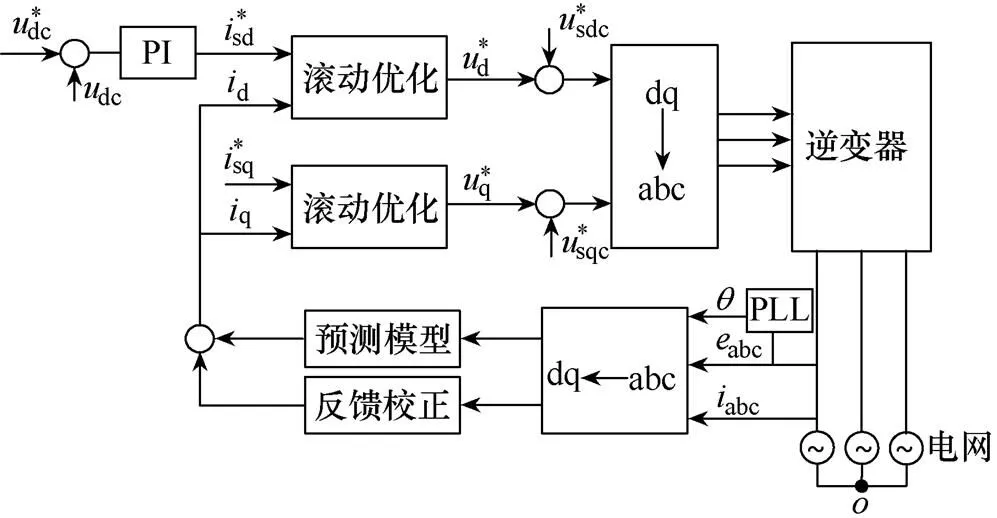
圖3 三相并網逆變器控制算法框圖
3 仿真驗證
建立三相并網逆變器的仿真模型,分別使用傳統的PI控制方法和所提出的MPC控制算法進行驗證比較。其中,采用在線計算的模型預測算法時,綜合考慮預測精度與預測算法的復雜程度,在不明顯降低系統控制品質的前提下盡可能減少預測算法的步長,從而盡可能減少控制算法的實時計算量,簡化控制算法。在PI控制算法中,PI調節器的參數為經過多次調整后得到的最優值。
基于以上考慮,本文所提出的模型預測控制算法采用3步預測,大致設定系數矩陣、及的取值如下:
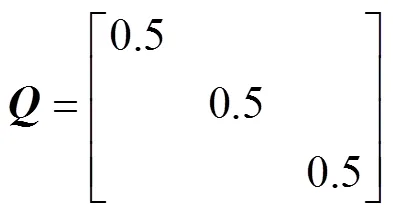
暫時停止電壓環的作用,直接指定d軸電流的參考值由20A階躍到80A,兩種控制算法的階躍響應如圖4所示。使用傳統的PI控制方法,電流上升至參考值約需30ms,并且在穩定狀態時d軸電流值會有幅度不等的波動,這種控制效果是由PI控制器本身的特性所決定的。采用本文所提出的MPC控制算法時,逆變器的d軸電流的階躍響應時間明顯縮短,電流的紋波較小,這是因為MPC算法在每一個控制周期內都能得到最優的控制變量的增量。
(a)PI控制法
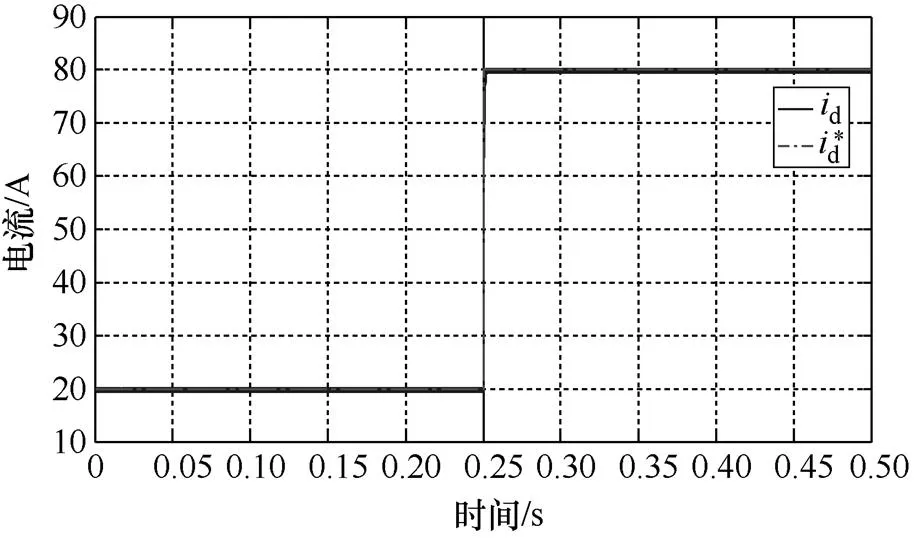
(b)MPC控制法
A相電網電壓與A相電流的波形如圖5所示,電流很快達到了設定值,并實現了單位功率因數并網。
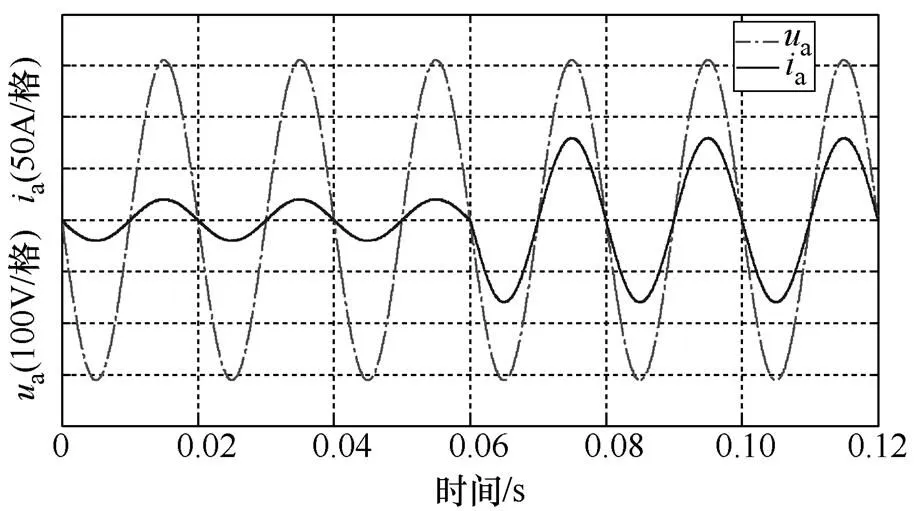
圖5 A相電壓電流波形圖
對逆變器穩定工作時的輸出電流進行諧波分析,結果如圖6(a)所示,其值僅為1.08%,滿足光伏并網規范的要求。設置交流側電感值為實際值的2倍,對此時逆變器的輸出電流進行諧波分析后得到如圖6(b)所示的結果,此時逆變器輸出電流的值僅為1.42%。由此可見,系統參數在較大范圍內變化都不會對控制效果造成明顯影響,說明MPC控制方法對系統參數也具有很好的魯棒性。

(a)L無誤差時的值
(b)L誤差100%時的值
圖6 并網電流諧波分析
4 結論
模型預測控制算法可以對受控系統未來若干個控制周期內的狀態量進行在線預測,基于預測值和性能指標函數求解得到最優的控制量,能夠以最小的代價實現對系統的最優控制。本文將模型預測控制應用于光伏并網逆變器的控制,取代傳統的電流環PI調節器,并在Matlab/Simulink環境下建立了算法的仿真模型。仿真結果表明,MPC控制方法能夠顯著地提高逆變器的響應速度,使逆變器具有較好的動靜態特性和較高的魯棒性,適用于光伏并網發電領域。同樣,這種基于模型預測控制的算法也可移植在風力發電等各類型并網逆變器、變頻器、整流器等設備上,具有廣泛的應用前景。
[1] 劉艷蘋. 太陽能光伏發電系統并網逆變器的研究[J]. 電源技術, 2013, 37(8): 1399-1401.
[2] 馬宏偉, 李永東, 鄭澤東, 等. 一種PWM整流器的模型預測控制方法[J]. 電力自動化設備, 2013, 33(11): 21-25.
[3] 楊圓圓. 模型預測控制研究與應用[D]. 大慶: 東北石油大學, 2006: 20-22.
[4] Kouro S, Cortes P, Vargas R, et al. Model predictive Control-A simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838.
[5] 鄭澤東, 王奎, 李永東, 等. 采用模型預測控制的交流電機電流控制器[J]. 電工技術學報, 2013, 28(11): 118-123.
[6] 鄭澤東, 陳寧寧, 李永東. 基于模型預測控制的異步電機弱磁控制新方法[J]. 電工技術學報, 2014, 29(3): 33-40.
[7] 李玉玲, 鮑建宇, 張仲超. 基于模型預測控制的單位功率因數電流型PWM整流器[J]. 中國電機工程學報, 2006, 26(19): 60-64.
Grid-connected PV Inverter Use a Modol Predictive Control Method
Chen Ningning1Song Zihao2Wang Zezhou1
(1. State Grid Zhejiang Haiyan Power Supply Company, Jiaxing, Zhejiang 314300;2. State Grid Jiangsu Electric Power Company Vocational Skill Training Base, Lianyungang, Jiangsu 222000)
A novel model predictive control (MPC) method is proposed base on mathematical model of the three-phase photovoltaic grid-connected inverters and the principle of MPC in this paper. The predictive model is acquired from the first-order difference equation of the inverter, then value of future sample cycles can be predictive, finally, the optimal control variables can be obtained by the rolling optimization, it has excellent performances and with hard robustness. The implementation process of the proposed method is described in detail, and the simulation model is established by Matlab/Simulink. The results of simulation proved that the proposed MPC control method has a quick response and with hard robustness, it’s very suitable for the PV inverter control in high-performance occasions.
PV inverter; model predictive control method (MPC); step response; robust
陳寧寧(1988-),男,江蘇省徐州市人,碩士,助理工程師,主要研究方向為配電網運維管理和配電網自動化。

