構建科學取向的數學教學設計能力培養體系

馬曉丹，張春莉

?

構建科學取向的數學教學設計能力培養體系

馬曉丹，張春莉

（北京師范大學教育學部，北京 100875）

構建科學取向的數學教學設計能力培養體系的重要意義在于指明數學教學設計能力培養的方向，建立數學教學設計中的三大聯系．基于科學取向教學論培養數學教學設計能力，建議從以下4個方面尋求突破：首先，明確科學取向教學論指導數學教學設計的意義；其次，解決數學教師在提升教學設計能力的過程中遇到的困惑；再次，立足學科特點，突出學科特色；最后，基于科學取向教學論實施數學教學設計能力的評價．

科學取向教學論；數學教學設計；教學目標；教學過程；教學評價

教學設計能力是教師專業能力的一個重要組成部分，它是教師在專業活動與行動中表現出的專業品質[1]．教學設計的取向與定位決定了教學設計的路徑與結果[2]．數學教學設計能力既包括數學教學設計的觀念，還包括數學教學設計的知識與技能[3]．反觀中國的數學教學設計，往往表現出各個教學活動之間是割裂的、獨立的，若能從數學本質和數學學習心理的角度對接下來的教學活動給出承上啟下的闡釋，不但能促進教學設計者思考設計該教學環節或教學活動的新課標精神，還能促進教學設計的執行者充分理解并更好地貫徹新課標的理念[4]．進一步來說，若要使數學教學設計有法可依、有據可循，則應當在深入剖析不同學段、不同課型的數學教學設計存在的問題的基礎之上，以認知心理學為理論基礎，探尋數學教學設計能力培養的途徑．正所謂“論立于此，若射之有的也，或百步之外，或五十步之外，的必先立，然后挾弓注矢以從之”．

1 明確當前數學教學設計存在的問題

2016年5月科學取向教學論在中小學學科教學中的應用研究（數學學科）課題組在廣州市花都區開展調研工作，面向小學、初中、高中3個學段，搜集新授課、講練課、復習課的數學教學設計共計70份．課題組對部分教師進行訪談，明確了當前不同學段、不同課型的數學教學設計存在的問題類型：

一是，教學目標模糊，具體表現為目標設置含糊不清，不能清晰地反映出希望學生達成的認知水平，混淆了學生經歷或體驗的過程與學習之后的學習結果．例如將目標表述為“進一步理解正數和負數的概念”，這里的“進一步理解”指的是“說出正數和負數的定義？”還是指“借助數軸解釋正數和負數的含義？”又或是“用正數和負數解釋生活中的問題？”可見，原先的表述并不清楚．再如設置諸如“增強觀察能力”的目標，這里的“觀察能力”究竟是學習結果？還是學習過程？若是學習結果，又該如何觀測？若是學習過程，是否想表達學生在觀察一段時間之后，能夠說出、寫出或畫出具體的數學對象？顯然，用“增強觀察能力”來設置目標，對教師而言，是不易觀測的；對學生而言，是不易操作的．

二是，教學過程隨意，這一類型表現為沒有遵循程序化的任務分析流程，缺少達成預期學習結果的學習條件，沒有建立不同數學知識類型與教學方法之間的聯系，教學方法的選擇沒有和學生的認知發展規律相結合．以“例1、例2、例3……”的形式呈現的是以“例題”為主線的教學設計，以“想一想”、“說一說”、“議一議”、“做一做”……的形式呈現的是以“活動”為主線的教學設計，將多個問題情境串成一個問題系列的是以“情境”為主線的教學設計．這只能說明近幾年數學教學設計在形式上的多樣性，并不意味著遵循了科學規范的教學步驟．以“圓的概念”為例，六年級將圓的定義概括為“到一個固定的點距離相等的所有點圍成的圖形”，九年級將圓定義為“到定點的距離等于定長的所有點的集合”，定義的變化反應出的是數學知識類型的變化，同時它們也應當遵循不同的學習規律．前者屬于具體概念的學習，后者屬于定義性概念的學習．相應地，前者應當將學生置于大量的事實例子中，形成圓的直觀認識，從而概括出圓的本質特征（例規法）；后者則是在學生理解“定點”、“定長”、“集合”等下位概念的前提下，定義圓的概念，再結合具體的例子加以說明（規例法）．因此，如何根據不同數學知識類型的特點，設計合理的教學方式實現預期的教學目標，使學生達到最佳的學習效果，這是數學教學設計所要解決的問題[5]．

三是，教學評價盲目，表現為缺少有針對性和時效性的數學測評試題，缺乏自我反思的有效途徑．如通過“指出在下列圖形中的圓”（測評）來考查學生是否能“舉例解釋圓的特征”（目標）是不合適的．“指出”即辨認，能夠勝任這一任務的學生達成的是概念性知識的記憶水平，這不足以說明學生已經達成高于記憶的理解水平，從而引發思考“車輪如何能滾動？井蓋為什么是圓的？”等更能夠測評出理解水平的試題．目標與測評在認知水平上是否一致是教學反思中的一項重要環節．

因此，目標的模糊性、過程的隨意性、評價的盲目性是當前數學教學設計能力培養需要解決的關鍵問題．如何對數學知識內容和學生認知水平進行更為精準的定位；如何區分數學課程標準中提及的“結果目標”和“過程目標”；如何區分達成教學目標所需要的多個中間目標以及它們的上下位關系；如何確定學生的起點能力；如何為教學內容提供與之匹配的學習條件；如何設計遵循信息加工順序的教學過程；如何根據不同的數學學習結果確定教學方法；如何確定學生已經達到既定的教學目標；如何對擬定的教學活動和評估試題進行調整等是對上述3個關鍵問題的進一步思考．

2 構建科學取向的數學教學設計能力培養體系的意義

國內外以研究教學規律為對象的理論，大致分為兩大類：一類是依據哲學和經驗總結所提出的理論，被稱為哲學取向教學論；另一類是依據科學心理學，尤其是學習心理學和實證研究所提出的理論，被稱為科學取向教學論[6]．“科學性”是高效教學行為的前提與歸宿，是指數學教師在教心、導學與發揮數學的教育性方面更具有合理性[7]．因此，構建科學取向的數學教學設計能力培養體系是必要的，其重要意義主要體現在以下兩方面．

2.1 指明了數學教學設計能力培養的方向

教學設計是運用系統方法分析教學問題和確定教學目標，建立解決教學問題的策略方案、試行解決方案、評價試行結果和對方案進行修改的過程[8]，是教師理論素養和學科素養的綜合體現．數學教學設計能力培養既要考慮一般意義上對教學設計能力的要求，還要考慮到當前數學教學設計能力培養需要解決的關鍵問題．因此，數學教學設計能力的培養目標應當從能夠設置精準的教學目標、設計科學規范的教學過程、組織及時有效的教學評價出發，自上而下地進行細化，最終形成數學教學設計能力培養體系（如圖1所示）；而數學教學設計能力則應當以準確把握數學課程標準中的內容與目標為出發點，自下而上地進行培養．

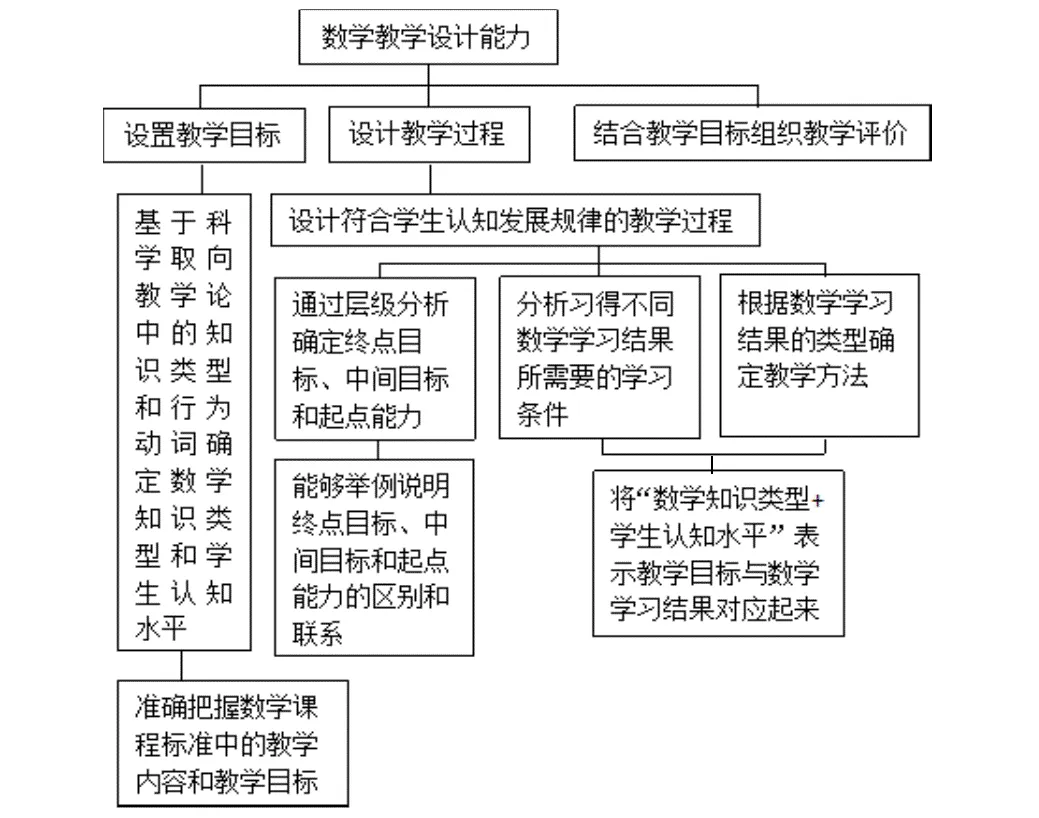
圖1 科學取向的數學教學設計能力培養體系（能力培養目標）

要想達成“準確地設置教學目標”、“科學規范地設計教學過程”需要諸多下位的培養目標作為前提條件．

在目標設置方面，首先要準確定位數學教材中靜態的知識所屬的類型，如表示“是什么”的基本事實與數學概念——“畢達哥拉斯定理就是我國的勾股定理”，“含有未知數的等式叫做方程”等；再如表示“怎么做”的程序性知識——“一元一次方程的求解分為5步：去分母、去括號、移項、合并同類項、系數化為1”等；其次要明確不同類型的數學知識在達成不同認知水平時（記憶、理解、運用、分析、評價、創造），將對應怎樣的學習結果，如對“一元一次方程求解的5個步驟”進行記憶、理解時，所習得的學習結果屬于數學基礎知識，也就是認知心理學中的言語信息，而當這一程序性知識達到運用及以上水平時所對應的學習結果屬于數學基本技能，也就是認知心理學中的智慧技能，這一程序性知識從較低的認知水平到較高認知水平的學習過程也是知識向技能轉化的過程．最后，能夠舉例說明終點目標（學習結束時應達到的目標）、中間目標（學習過程中必須達到的目標）和起點能力（學習開始之前已經具備的數學基礎知識、基本技能、基本思想方法、基本活動經驗）之間的區別和聯系，以“加權平均數”為例，要想達成“能用公式正確計算加權平均數，并利用計算結果來分析數據”這一終點目標，需要以“能夠陳述出權的作用，并能夠舉例說明權的不同表達方式”、“能說出算術平均數和加權平均數的區別和聯系”等中間目標為前提，歸根究底要以“能夠計算算術平均數”為達成上述中間目標的起點能力．

在過程組織方面，教師要分析不同數學學習結果所需的學習條件，這里的學習條件包括由學習者自身或數學知識本質決定的必要條件，如“全等三角形的性質和判定”是學習“相似三角形的性質和判定”的必要條件；還包括使學習更容易、更迅速、只起輔助作用的支持性條件，如學生在掌控圓規等數學工具時所需要的動作技能和數學學習過程中表現出的情感態度等；以及源于學習環境和教學者提供的外部條件，如圖形計算器等技術工具以及教師配合概念學習給出的正反例證等．此外，教師還要根據數學學習結果的類型確定教學方法，如理解“哪一類數學學習結果一定要有正反例證，并加以強化和反饋”，“哪一類數學學習結果一定要結合樣例學習，并設計變式練習”，等等．

2.2 建立數學教學設計中的三大聯系

基于科學取向教學論的數學教學設計能力研究建立了數學學習結果類型與學習條件間的聯系，數學學習結果類型與教學方法間的聯系，以及教學目標、教學過程與教學評價的聯系．

2.2.1 數學學習結果類型與學習條件間的聯系

數學學習結果分為數學知識（即狹義的數學知識，對應認知心理學中的言語信息）、數學智慧技能、數學思想方法、數學問題解決和態度5種類型，每一類型下又分若干亞類，如數學知識包括符號表征學習、事實學習和數學關系的心理模型；數學智慧技能包括具體概念、定義性概念、規則和高級規則[9]．不同的數學學習結果需要不同學習條件的支持．如數學知識的學習以原有知識結構為基礎，需要提供學習者辨別新舊知識的外部條件；數學具體概念的學習需要學生能夠辨別認知結構中已有具體概念的例子，并在辨別的基礎上總括出下位例子中蘊含的概念；數學定義性概念的學習以構成定義的相關具體概念為前提條件，或者學生的認知結構中具有同化下位概念的上位的一般概念或類似概念；數學規則的學習需要在概念的基礎上學習；數學問題解決的學習是在簡單規則基礎上學習復雜規則；數學思想方法是在數學智慧技能達到相對自動化后形成的，并需要某些基本心理能力和認知發展水平的支持；數學情感態度的習得需要數學知識、數學智慧技能以及其它態度的支持[10]．

2.2.2 數學學習結果類型與教學方法間的聯系

數學學習結果類型與學習條件建立聯系的同時，也建立了與教學方法的聯系．如對數學知識進行不斷地強化，要把數學具體概念的學習暴露在充分的正反例證中；為數學定義性概念的學習提供揭示概念本質特征的例子；通過樣例學習和變式練習來實現數學規則的遷移與運用，提供及時的反饋并在關鍵處給予指導；為數學問題解決提供突出圖式的原型，將學生暴露在大量的圖式例子當中并伴隨及時的反饋；最終引導學生進行積極的歸因以促進學生價值觀的形成[11]．

2.2.3 教學目標與教學過程及教學評價的聯系

修訂后的布盧姆教育目標分類學能夠有效地引領教師從知識類型和認知過程兩個維度確定教學目標、設計教學過程，對提高教學品質與效率有重要的指導作用[12]．與此同時，教學目標的精準定位為教師的教學評價提供了有力的依據．這里的教學評價是指根據教學目標中的知識類型和認知水平制定的評價計劃，并對評價結果做出解釋[9]．高質量的教學需要伴隨高質量的測評，否則高質量的教學也無助于提高學生的測評成績[13]．因此，修訂版分類學的重要成果之一就是將教學目標、教學活動以及教學評價置于同一個分類表中進行一致性的檢驗[14]．如表1所示，目標2、教學活動2和測評2三者出現在同一方格中，表示一致性程度高．目標1和測評1（目標3和活動3）二者出現在一個方格中，說明一致性程度較差，需要研究者重新審視這部分目標、活動和測評的設置．

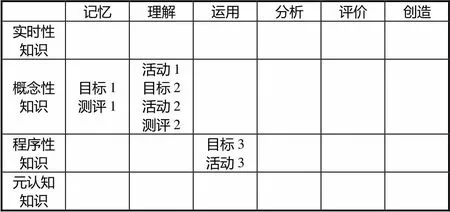
表1 “圓的認識”案例：目標與教學活動及測評的一致性問題

注：目標1=能夠指出圓的各部分的名稱．

目標2=能夠用圓的知識來解釋生活中的想象或用生活中的現象來解釋圓的特征．

目標3=能使用工具畫出圓．

活動1=折一折手中的圓形紙片，看看你都發現了什么？

活動2=給出長方形、正方形、平行四邊形、梯形、三角形、長方體和圓柱體的圖片，提問學生圓與他們相比，有什么不同的地方？

活動3=學生從扎釘、一根線、一個皮筋以及一根鉛筆中選擇材料制作畫圓的工具．

測評1=指出圓的半徑和直徑．

測評2=生活中哪些地方離不開圓？

3 實施科學取向的數學教學設計能力培養的建議

3.1 明確科學取向教學論指導數學教學設計的意義

教師的教學設計觀念根深蒂固，信念和知識影響著他們設定教學目標，處理教材，設計教學任務，實施教案[15]．認真分析一些優秀的教學設計后常能發現，這些教師往往潛在地運用任務分析等技術，只是沒有得到理論層面的解釋．當然，需要承認，不是所有優秀的教學設計都是在科學取向教學論的指導下完成的，但凡是優秀的教學設計都可以通過科學取向教學論進行解釋并能經得起教育教學實踐的檢驗．這些優秀的教學設計之所以沒有達到技術層面，而僅僅停留在經驗層面難以推廣，就是因為缺乏基于教育學和心理學理論的詮釋與概括．如上所論述的有關科學取向教學論對教學設計能力培養的重要意義，如果不能在相關培訓中得以明確，而是直接進行教學設計技術上的指導，那么最終的培訓效果無非是事倍功半．數學教學設計信念會指引教師開展教學設計，實施教學設計活動，教師擁有合理的數學教學設計信念是下一步進行教學實踐的前提和保障[16]．因此，基于科學取向教學論培養數學教學設計能力的意義不僅在于對教師教學能力的提高，更是在尋求教師教學信念上的轉變．

3.2 解決數學教師在提升教學設計能力的過程中遇到的困惑

隨著現代認知心理學的發展，科學取向教學論取得了豐碩的成果，形成了更為科學、規范、具體的教學設計體系，為教師的教學設計提供了充分的心理學依據．與此同時，相對專業的話語體系對一線教師運用科學取向教學論指導自身教學設計帶來困難．課題組在廣州市花都區對一線數學教師進行了訪談，了解到教師對科學取向教學論存在的困惑主要包括：（1）知識類型與內容領域是什么關系？前者是根據信息加工學對信息編碼方式的不同進行的劃分，因此不同的知識類型對應不同的學習機制[11]，后者是按照知識表征的形式進行的劃分，如中國義務教育階段將數學學科劃分為數與代數、空間與圖形、統計與概率、實踐與綜合應用4大領域．事實上，并不是每一種教學方法都適用于所有的數學內容[17]．按照現代心理學的觀點，如果不同的內容領域的知識具有相同的信息編碼方式則對應相同的學習機制和相似的教學方法．（2）為什么要用“行為動詞+名詞”的形式描述教學目標？行為動詞決定認知水平，名詞決定知識類型，對知識類型和認知水平進行精準定位，可以形成可觀察、可測量的教學目標，并能指導教學評價[14]．如將目標“進一步理解正數和負數的概念”改為“用生活中的實際問題解釋（動詞）正數和負數的意義（名詞）”，則有助于教師了解學生應該達到的和已經達到的認知水平．（3）概念性知識與具體概念、定義性概念的區別是什么？概念性知識是修訂版布盧姆教育目標分類學所提出的知識類型，如數學教材中表示“是什么”的知識；而具體概念、定義性概念屬于智慧技能，是學習者在學習之后達成的學習結果．每一種學習結果都可以看作是教材中不同類型的知識在不同的認知水平上的表現．值得注意的是，教材中的概念性知識并不能在所有的認知水平上表現為數學智慧技能，如“=”、“”等概念在記憶、理解水平進行學習時所達成的學習結果只是一種數學符號語言．因此，適時、及時地解決好上述困惑對于數學教師運用科學取向教學論指導自身教學設計具有重要意義．

3.3 立足學科特點突出學科特色

依據數學課程標準的理念與要求，數學教師的專業素養應體現教師與數學學科的雙重特性，需要與數學專業從業者和其它學科的教師有所區別，并同時體現出教師工作的實踐取向[18]．數學教學設計能力作為數學教師的專業素養之一，需要構建有別于其它學科的數學學習結果分類系統，并給出具體的數學例子（如表2所示）．

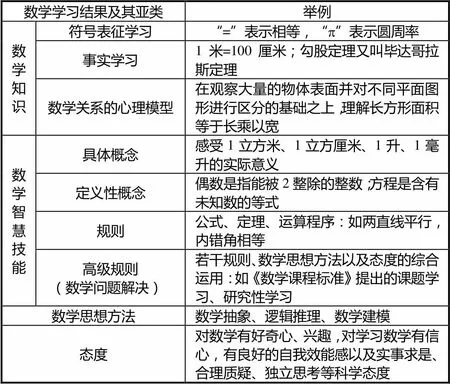
表2 數學學習結果及舉例

學習“=”、“p”等符號的意義，都屬于符號表征的學習；記住“1米=100厘米”，“勾股定理又叫畢達哥拉斯定理”等相對具體且不具有概括性的事件都屬于事實學習；“在觀察大量的物體表面并對不同平面圖形進行區分的基礎之上，理解長方形面積等于長乘以寬”，是客觀事物在人腦中的表征，即數學關系的心理模型．符號表征學習、事實學習和數學關系的心理模型都屬于數學知識的范疇[9]．

感受“1立方米”、“1立方厘米”等的實際意義，是運用一類事物的關鍵屬性對事物進行分類的學習，屬于數學具體概念；諸如“偶數是指能被2整除的整數”、“方程是含有未知數的等式”等以下定義的方式闡明概念的關鍵特征，屬于數學定義性概念；數學學習過程中習得的公式、定理、運算程序等是學生運用若干概念之間的關系或程序對外辦事的能力，即數學規則；若干數學規則的綜合運用常伴隨數學思想方法和態度的綜合運用，如課題學習、研究性學習等都屬于高級規則，相當于數學問題解決．數學具體概念與定義性概念、數學規則與高級規則都屬于數學智慧技能的范疇[9]．

數學思想方法是指支配學習者如何學習、如何思考、如何問題解決的一套對內調控的能力．如分類思想、集合思想、歸納思想、演繹思想、函數思想、方程思想等都是數學思想方法．史寧中教授將抽象、推理和模型作為數學思想高度概括的結果，并稱之為數學基本思想[19]．數學思想方法是數學基本思想下位的概念，具有一定的可操作性的，同時反映數學的某些思想，與一般意義上的具體方法不同[20]．態度是在數學學習過程中，對數學課程或數學知識技能本身形成的行為傾向，包括對數學有好奇心、興趣、自信心，有良好的自我效能感以及實事求是、合理質疑、獨立思考等科學態度[9]．

3.4 基于科學取向教學論實施數學教學設計能力評價

科學取向教學論為數學教學設計能力培養指明的方向也是為數學教師教學設計能力評價指明的方向．數學教學設計能力的評價從以下3個方面著手：一是要評價教師的目標設置和目標陳述，包括知識類型與認知過程的定位是否準確，目標是否具有可操作性和可觀察性．二是要評價教師的教學過程，包括任務分析和教學步驟．對任務分析的評價包括能否將知識類型與認知水平準確地對應到數學學習結果；能否通過層級分析確定學生的中間目標和起點能力；能否分析習得數學學習結果所需要的學習條件；能否結合層級分析判斷教學的重點和難點、選擇需要的教具和學具等．對教學步驟的評價包括是否設置與教學目標相關的導入或情境，以達到“引起注意與告知目標”的目的；是否安排與起點能力相關的復習，以達到“提示學生回憶原有知識”的目的；是否遵循從起點能力到中間目標再到終點目標的層級順序，以達到“呈現有組織的信息”的目的；是否建立起新舊知識的聯系，將新知識建構在已有的認知圖式中，以達到“闡明新舊知識關系，促進理解”的目的；是否針對關鍵屬性設計變式練習，以促進數學知識認知結構的重組與改組，促進數學知識向數學智慧技能和思想方法的轉化，以達到“對復習與記憶提供指導”的目的；是否提供提取數學知識的線索或應用數學智慧技能的新情境，以達到“知識的運用和遷移”的目的．三是對教師的教學評價進行評估，如所選擇的數學試題是否與教學目標、教學活動在認知水平上是一致性的[11]．

科學取向的數學教學設計能力培養體系的建構為數學教師教學設計培訓課程提供了依據．課題組從廣州市花都區的調研中了解到，數學教師接受的培訓內容主要圍繞數學教學理論、數學方法論、數學教學設計研究、數學思想方法與教學研究、數學文化與數學課堂教學、數學教材教法、數學教學策略、數學教育技術以及中高考命題研究等．該調研結果與陳向明、王志明（2013）進行的“義務教育階段教師培訓調查：現狀、問題與建議”中提到的：“較高比例的被調查者認為自己接受最多的培訓內容前3位是教育教學理論、學科教學、教學方法及策略”的研究結論基本一致[21]．也就是說，大多數數學教師了解教材中的知識體系，清楚教材中例題習題的難易程度，理解教材的設計意圖（章引言的作用、數學活動與本章內容的聯系等），能夠對學生進行學情分析，知道基本的教學方法（講授法、發現法、探究法等），具備教學設計的基本教育經驗．基于科學取向教學論的數學教學設計能力培養則是教師在基本教育經驗的基礎之上尋求更為行之有效的教學設計路徑，如在教師研讀教材的基礎之上，明確數學學習結果的層級關系，引導教師組織教學內容；基于教師對學生的學情分析，指導教師設計符合學生認知發展規律的教學；根據教師對教法的了解，建立起數學學習結果與教學方法的聯系等．

[1] 左坤．初中數學教師教學設計能力研究[J]．數學教育學報，2011，20（2）：41-44．

[2] 吳寶瑩，陳敏．數學教學設計的取向與定位[J]．數學教育學報，2012，21（3）：89-90．

[3] 李孝誠，綦春霞，史曉鋒．初中數學教師教學設計能力發展的實證研究——基于網絡研修共同體教師專業發展的個案研究[J]．中國電化教育，2013，（3）：56-61．

[4] 沈威，盧建川，曹廣福．美國紐約CCSSM背景下小學數學教學設計的特點與啟示[J]．外國中小教育，2014，（10）：60-65．

[5] 王光生．知識類型與數學教學設計[J]．數學教育學報，2007，16（3）：27-31．

[6] 皮連生，吳紅耘．兩種取向的教學論與有效教學研究[J]．教育研究，2011，（5）：25-30．

[7] 王光明．高效數學教學行為的特征[J]．數學教育學報，2011，20（1）：35-38．

[8] 烏美娜．教學設計[M]．北京：高等教育出版社，1994．

[9] 張春莉，王小明．數學學習與教學設計（中學卷）[M]．上海：上海教育出版社，2004．

[10] 加涅．教學設計原理[M]．皮連生譯．上海：華東師范大學出版社，1999．

[11] 皮連生．教育心理學（第四版）[M]．上海：上海教育出版社，2011．

[12] 李昌官．布盧姆認知目標新分類指導下的數學教學設計——以“數系的擴充和復數的概念”教學設計為例[J]．數學教育學報，2012，21（3）：67-71．

[13] 張春莉，馬曉丹．布盧姆教育目標分類學修訂版在數學學科中的應用[J]．課程·教材·教法，2017，（1）：119-124．

[14] ?L·W·安德森．學習、教學和評估的分類學：布盧姆教育目標分類學修訂版[M]．皮連生譯．上海：華東師范大學出版社，2008．

[15] ?Yang X.[M]. Conception and Characteristics of Expert Mathematics Teachers in China. Springer Fachmedien Wiesbaden, 2014.

[16] 馮振舉，王惠揚子．職前數學教師教學設計信念轉變的個案研究——以HPM視角下的勾股定理教學為例[J]．數學教育學報，2016，25（2）：59-65．

[17] ?Soedjadi R.[C]. Proceedings of the Ninth International Congress on Mathematical Education. Springer Netherlands, 2004.

[18] 章勤瓊，徐文彬．試論義務教育數學教師專業素養及其結構——基于教師專業標準與數學課程標準的思考[J]．數學教育學報，2016，25（4）：69-73．

[19] 史寧中．漫談數學的基本思想[J]．數學教育學報，2011，20（4）：8．

[20] 馬云鵬．關于數學核心素養的幾個問題[J]．課程·教材·教法，2015，（9）：36-39．

[21] 陳向明，王志明．義務教育階段教師培訓調查：現狀、問題與建議[J]．開放教育研究，2013，（4）：11-19．

Establishment of Cultivation System of Science-oriented Mathematics Instruction Design Competence

MA Xiao-dan, ZHANG Chun-li

(Faculty of Education in Beijing Normal University, Beijing 100875, China)

Establishing a cultivation system of science-oriented mathematics instruction design competence had important significance. It pointed out the direction of promotion and establishes three links in mathematics teaching-planning. Establishing a cultivation system of science-oriented mathematics instruction design competence included four suggestions: Firstly, we should make clear the value of science-oriented instructional theory to guide the design of mathematics teaching. Secondly, we should solve the problems which mathematics teachers encountered in the process of improving teaching design ability. Thirdly, we based on the characteristics of mathematics and highlight characteristics of the subject. Eventually, we implement evaluation of science-oriented mathematics instruction design competence.

science oriented teaching theory; mathematics teaching design; teaching goal; teaching process; teaching evaluation

[責任編校：周學智]

G420

A

1004–9894（2017）04–0056–05

2017–04–01

北京市教育科學“十二五”規劃重點課題——專家教師原型觀下課堂教學執行力的提升（AIA15226）

馬曉丹（1989—），女，天津人，博士生，主要從事數學教育研究．