脈沖加砂壓裂支撐劑鋪置狀態的CFD模擬

李凌川，張永春，李月麗

(中石化華北油氣分公司石油工程技術研究院，河南 鄭州 450006)

脈沖加砂壓裂支撐劑鋪置狀態的CFD模擬

李凌川，張永春，李月麗

(中石化華北油氣分公司石油工程技術研究院，河南 鄭州 450006)

脈沖加砂壓裂過程中，支撐劑的有效鋪置是形成高速油氣滲流通道及獲得高裂縫導流能力的基礎條件。針對物理模擬實驗受裝置承壓能力、泵注排量和材料成本限制等缺點，應用CFD(計算流體力學)方法模擬計算了攜砂液與中頂液交替注入時的流動狀態，分析了不同黏度比、注入速度及脈沖間隔時間對支撐劑鋪置狀態的影響。研究結果表明，增大攜砂液與中頂液黏度比，通道率與支撐劑有效鋪置距離減小，支撐劑簇團分散效果變差，現場施工時黏度比不宜超過5；注入速度增大，支撐劑有效鋪置距離和通道率增大，但支撐劑分散性變差，綜合考慮通道率和砂團分散效果，折算現場合理施工排量為3.2～4.3m3/min；過短或過長的脈沖間隔時間均不利于有效滲流通道的形成，脈沖間隔時間為整個脈沖周期的0.5～0.6倍時效果較好。

脈沖加砂壓裂；支撐劑；CFD模擬；黏度比；注入速度；間隔時間

20世紀60年代以來，為獲得更高的人工裂縫導流能力，壓裂專家們提出了一系列重要改進措施，如提高支撐劑強度和圓球度，降低壓裂液殘渣滯留傷害，使用潤濕劑、增能壓裂液和清潔壓裂液等[1]，這些措施都是圍繞連續充填裂縫方式下獲得理論上的最大導流能力這一目標，而部分壓后評估測試結果表明，實際生成的裂縫導流能力遠未達到設計最優值[2]。與常規加砂壓裂的支撐劑連續充填方式不同，脈沖加砂壓裂通過特殊混砂設備，高頻交替注入攜砂液和不含支撐劑的中頂液，以實現人工裂縫內支撐劑的非均勻鋪置和縫內有效孔道率的提升[3]，既減少了支撐劑用量，又同時提高了裂縫導流能力。

脈沖加砂壓裂思想最初源于J.M. Tinsley[4]和M. A. Parker等[5]提出的采用非連續鋪砂方式提高人工裂縫內孔道率，與常規連續鋪砂支撐裂縫相比，其導流能力大幅提升；M. Gillard等[6]于2010年首次提出高速通道壓裂技術，以縫內支撐劑多層非均勻鋪置提高人工裂縫導流能力；國內研究方面，戚斌等[1]于2013年在川西地區開展了脈沖柱塞加砂壓裂先導試驗；錢斌等[3]于2014年在蘇里格桃7區塊完成了國內首次自主化脈沖加砂壓裂技術的現場先導試驗；吳順林等[7]于2014年在鄂爾多斯盆地某低滲透區塊選取了3口直井，開展脈沖加砂壓裂試驗；楊衍東等[8]于2015年在中江氣田應用了4口水平井的脈沖柱塞加砂新工藝。綜上所述，國內對脈沖加砂壓裂的研究多數以工藝應用為主，而關于脈沖加砂壓裂過程中支撐劑鋪置狀態的研究相對較少，物理模擬實驗雖然可以直觀清楚地展示支撐劑的運移和沉降，但受實驗裝置承壓能力、泵注排量和材料成本的限制，無法實現高壓力、高排量和多因素的模擬研究，而近年來不斷發展的計算流體力學(CFD)，為解決壓裂過程中的流體工程實際問題提供了一種新手段。

1 支撐劑運移歐拉-歐拉模型

脈沖加砂壓裂時，攜砂液和中頂液交替注入，該過程包含了復雜的液-固兩相流動，描述液-固兩相流動的數值模型主要有歐拉-拉格朗日模型和歐拉-歐拉模型，其中歐拉-歐拉模型將顆粒看作成一種擬流體，認為顆粒相和流體相是共同存在且相互滲透的連續介質，又稱歐拉雙流體模型[9]，與歐拉-拉格朗日模型相比，歐拉雙流體模型具有計算量小、研究成果豐富等優點，是今后工程多相流問題研究的首要選擇[10]。

描述歐拉-歐拉模型的數學方程[11～13]如下。

1.1質量守恒方程

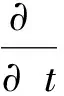
(1)

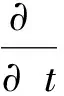
(2)

式中：t為時間，s；α為體積分數，1；ρ為流體密度，kg/m3；v為速度，m/s；下標l、s分別表示液相和固相。

1.2動量守恒方程

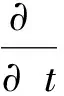
(3)

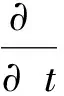
(4)

式中：p為分壓，Pa；τ為剪切應力張量，Pa；g為重力加速度，m/s2；β為相間動量交換系數，kg/(m3·s)。

1.3顆粒動能守恒方程

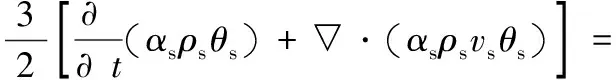
(5)

式中：θs為顆粒溫度，K；κs為顆粒能量傳導系數，kg/(m·s)；γs為顆粒相波動動能碰撞耗散，kg/(m·s3)。式中冒號：為張量運算符號，表示張量的雙點積。

根據Gidaspow模型，液-固兩相間的動量交換系數β為:

(6)

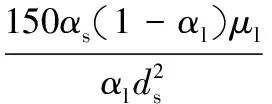
(7)

其中:

(8)

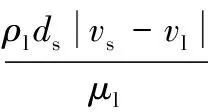
(9)

式中：CD為相間動量交換阻力系數，1；ds為固相顆粒直徑，m；μl為液相黏度，Pa·s；Res為以相間滑移速度定義的雷諾數，1。

2 幾何模型及邊界條件

模擬對象采用戚斌等[1]設計的透明裂縫物模裝置(圖1)，該裝置的模擬縫長100cm，縫高30cm，縫寬0.6cm，裂縫總體積為1800mL；以某區塊的一口脈沖壓裂井為例，該井壓后數據擬合表明，人工裂縫單翼縫長170m，縫高30m，縫寬6mm，按照相似原理，當現場施工排量為3m3/min時，縫口平均流速為0.139m/s，對應實驗泵注排量為0.9m3/h。

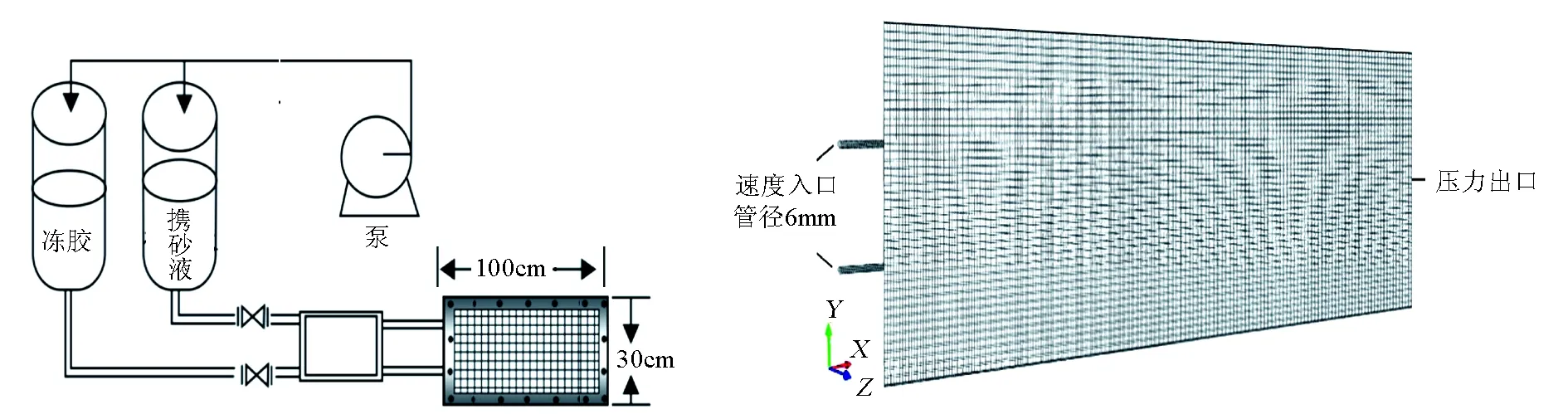
圖1 脈沖柱塞加砂流態物模示意圖 圖2 幾何模型及網格劃分示意圖(100cm×30cm×0.6cm)

數值模擬的裂縫尺寸與物理模型相同，利用前處理軟件建立模擬對象的幾何模型并進行網格劃分，裂縫左側2根直徑6mm、Y向間距10cm的管子為入口位置，裂縫右側為出口位置，流體流向為X軸方向；網格劃分過程中，考慮到裂縫模型的形狀較為規則，同時兼顧計算速度和穩定性，模型全部采取六面體網格，總共劃分36860個網格單元。

入口邊界條件為速度入口，出口采用壓力出口邊界條件，設定表壓為0MPa，第二相回流體積分數為0，表示攜砂液或中頂液流出裂縫出口后不再返回計算域重復計算；其他設為無滑移固壁邊界條件。數值模擬時壓裂液為凍膠，黏度90mPa·s，密度1.1g/cm3，支撐劑為20/40目陶粒，體積密度1.6g/cm3，顆粒密度3.1g/cm3，平均粒徑0.6mm。

初始化采用入口邊界條件，控制方程離散格式為一階迎風格式，流場迭代求解方法為PISO算法，收斂標準為各項殘差小于10-4，取縫寬方向中心截面進行模擬結果分析。

3 結果及討論

3.1與物模試驗對比

戚斌等[1]在文獻中指出當攜砂液和中頂液間隔注入時，通過調速泵將不同的液體以不同速度注入裂縫模型中，從而模擬現場施工中脈沖加砂的過程。攜砂液和中頂液交替注入模擬裂縫中的流態及破膠后的支撐劑剖面如圖3所示，從圖3可以看出，攜砂液在破膠后形成了非均勻的溝壑狀滲流通道，這種開放性的滲流通道正是脈沖加砂壓裂所期望的油氣高速滲流通道，通道的大小及數量對裂縫導流能力和壓后產能影響較大，為精確評價脈沖壓裂支撐劑鋪置效果，這里引入通道率的概念。通道率是指通道體積與支撐裂縫總體積之比，即:

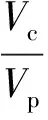
(10)

式中：Rc為通道率，%；Vc為通道體積，m3；Vp為支撐裂縫總體積，m3。

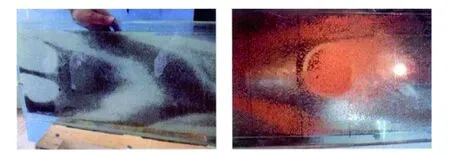
圖3 脈沖加砂流態及破膠后支撐劑剖面

由于文獻[1]中沒有指明圖3的注入速度和壓裂液黏度，因此筆者選擇入口速度為0.15m/s，壓裂液黏度為90mPa·s，黏度比R=1(黏度比定義為攜砂液黏度與中頂液黏度之比)，脈沖周期T=60s(攜砂液注入時間與中頂液注入時間之和為一個脈沖周期，這里設攜砂液注入時間與中頂液注入時間均為30s)的條件與物模實驗進行對比，模擬結果如圖4所示。

圖4(a)為攜砂液注入30s后形成的支撐劑剖面；圖4(b)對應中頂液注入30s后，將支撐劑推向裂縫深處，形成類似反“C”字的剖面形狀，此時完成一個脈沖周期；圖4(c)對應繼續交替注入攜砂液后，支撐劑鋪置范圍進一步向裂縫深處擴展；圖4(d)則為中頂液注入10s后的支撐劑分布狀態，對比實驗結果圖3可以發現，兩個支撐劑段塞之間形成了類似的溝壑狀滲流通道，表明建立的數值模型能夠較為準確地捕捉脈沖加砂過程中支撐劑剖面形態的變化，數值模擬結果與物模試驗結果符合度較高。

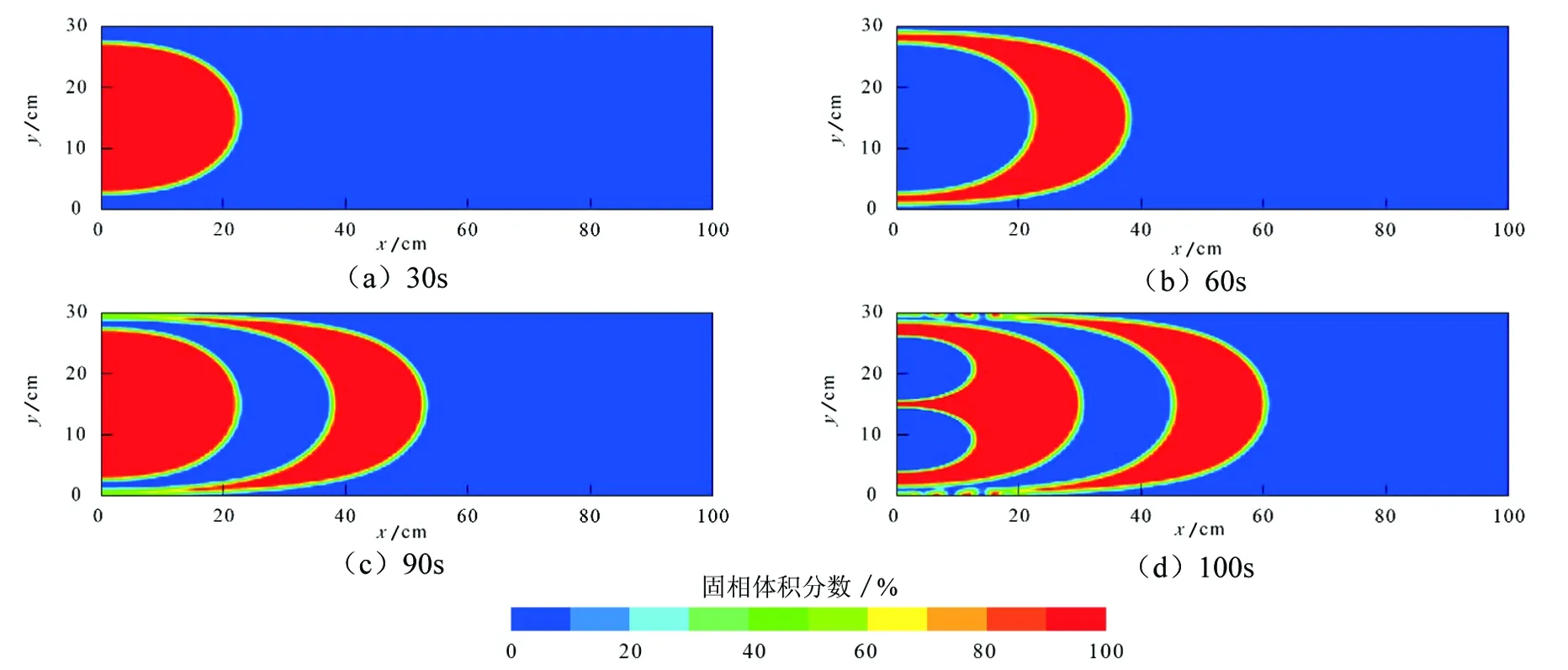
圖4 數值模擬結果與物模試驗對比(R=1)

3.2黏度比的影響

保持注入速度v=0.15m/s和脈沖周期T=60s不變，通過減小中頂液黏度，分析不同攜砂液和中頂液黏度比對支撐劑鋪置狀態的影響及通道率的分布情況(總共注入6個脈沖周期)，結果如圖5和圖6所示。

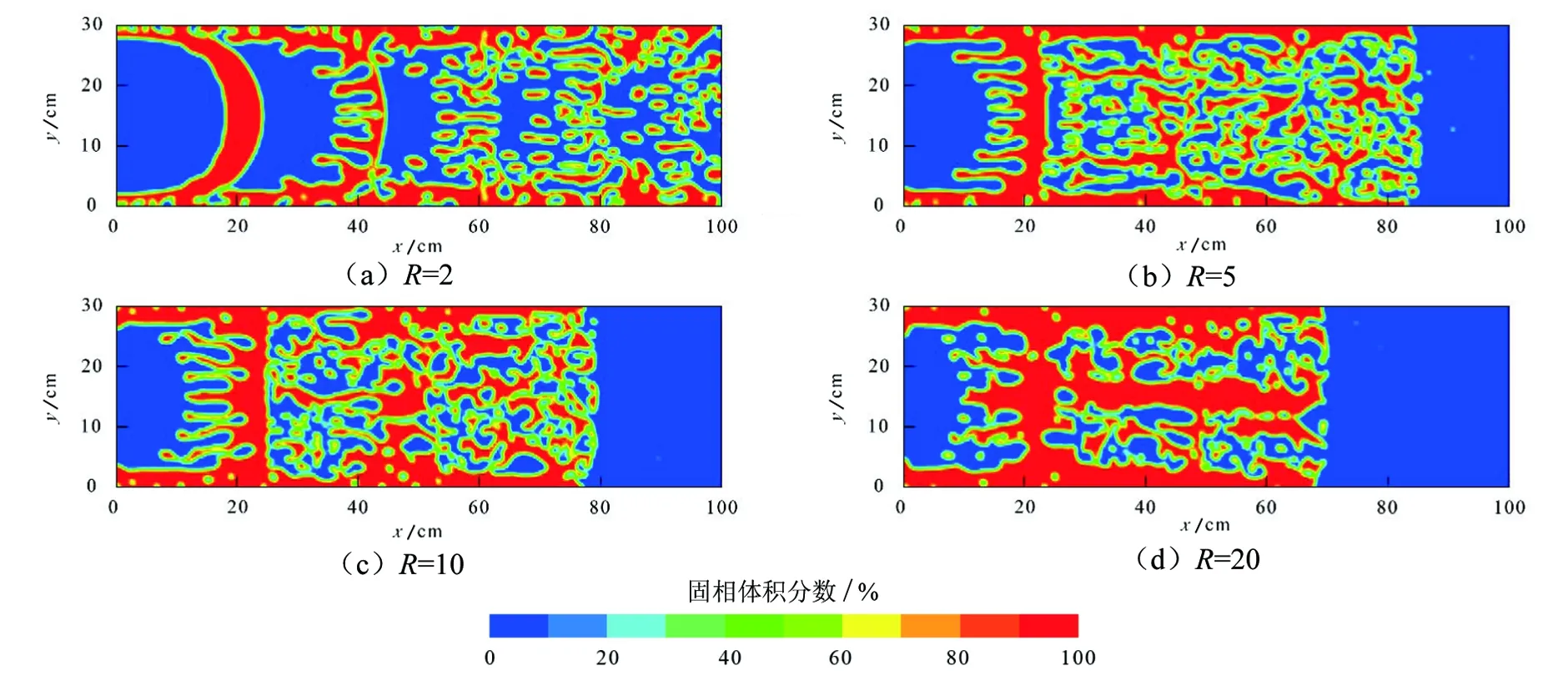
圖5 不同黏度比時的支撐劑鋪置形態

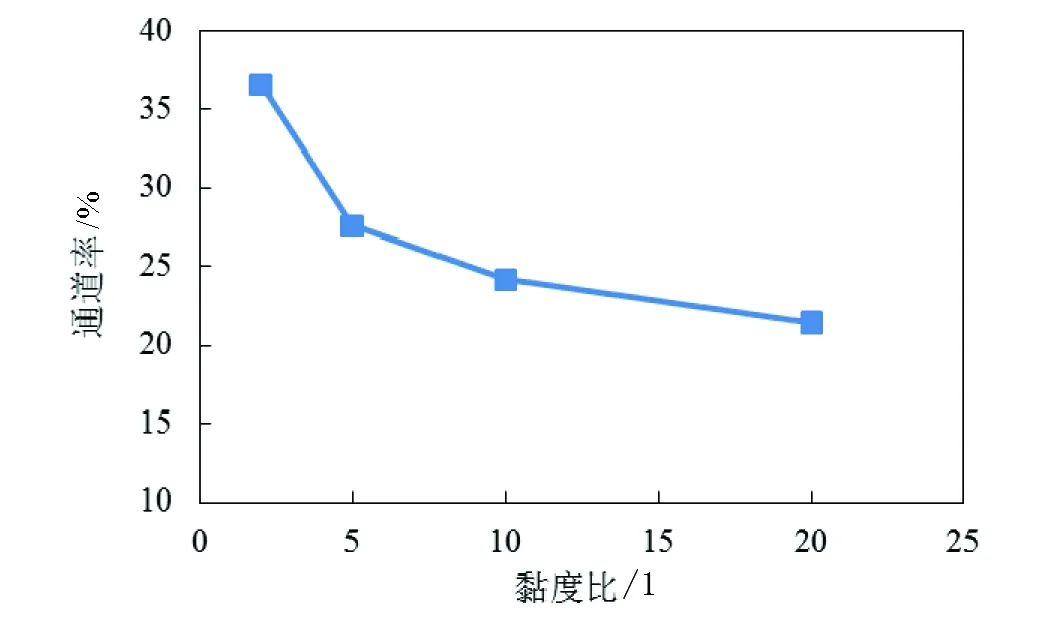
圖6 不同黏度比下的通道率分布

從圖5和圖6可以看出，隨著黏度比的不斷增大，通道率逐漸減小，支撐劑在縫長方向的有效鋪置距離也隨之減小，黏度比R=2時支撐劑鋪置距離為100cm(圖5(a))，而當黏度比增大到20時鋪置距離僅為70cm(圖5(d))。這是因為在較低的黏度比下，攜砂液與中頂液之間的速度差異較小，中頂液驅替前沿基本為均勻推進(圖4(d))；而隨著黏度比的不斷增大，攜砂液與中頂液間的速度差異也隨之增大，這使得低黏度的中頂液滲入并繞過高黏度的攜砂液，產生類似于水驅油過程中的“黏性指進”現象，阻礙了支撐劑在縫長方向的有效鋪置，從圖7的速度矢量圖也可以看出，中頂液指進前沿的流體速度明顯高于其他區域，進一步說明指進是由于速度場分布不均所引起。

當黏度比R=5時(圖5(b))，支撐劑簇團分散較均勻，通道率較大，且有效支撐距離較長，與黏度比R=2(圖5(a))和R=1(圖4(d))時相比，可避免兩個支撐劑段塞間的通道過大而造成裂縫閉合的情況；當黏度比增大到20后，由于指進現象加重，支撐劑簇團分散效果變差，縫長方向的有效鋪置距離減小。因此，建議現場施工時攜砂液與中頂液黏度比不宜超過5。

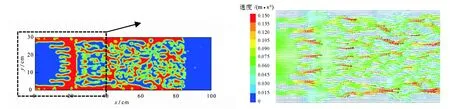
圖7 液相速度矢量圖(R=5)

3.3注入速度的影響

選取攜砂液和中頂液黏度比R=5，脈沖周期T=60s，總共注入6個脈沖周期，改變注入速度分別為0.1、0.15、0.2、0.3m/s，模擬注入速度對支撐劑鋪置的影響及通道率的分布情況，結果如圖8和圖9所示。

從圖8和圖9可以看出，隨著注入速度增加，中頂液前沿指進現象加重，通道率增大，但增大趨勢逐漸放緩，支撐劑有效鋪置距離增加，但砂團分散效果變差。這是因為注入速度增大，中頂液與攜砂液間的速度差異增大，導致中頂液前沿指進現象加重，并且注入速率較大時，在相同時間內進入裂縫的攜砂液與中頂液體積量也相對較多，因而高注入速率下的支撐距離和通道率會有所增加，但并非注入速度越大越好。綜合考慮通道率和砂團分散效果，當注入速度為0.15～0.2m/s時效果較好，根據相似原理，折算現場施工排量為3.2～4.3m3/min。同時值得注意的是，中頂液注入后近井地帶裂縫會出現大片的支撐劑空白區域，為避免近井地帶裂縫閉合，建立裂縫與井筒的有效溝通，泵注程序的最后階段需要尾追一個時間相對較長的連續支撐劑段塞。

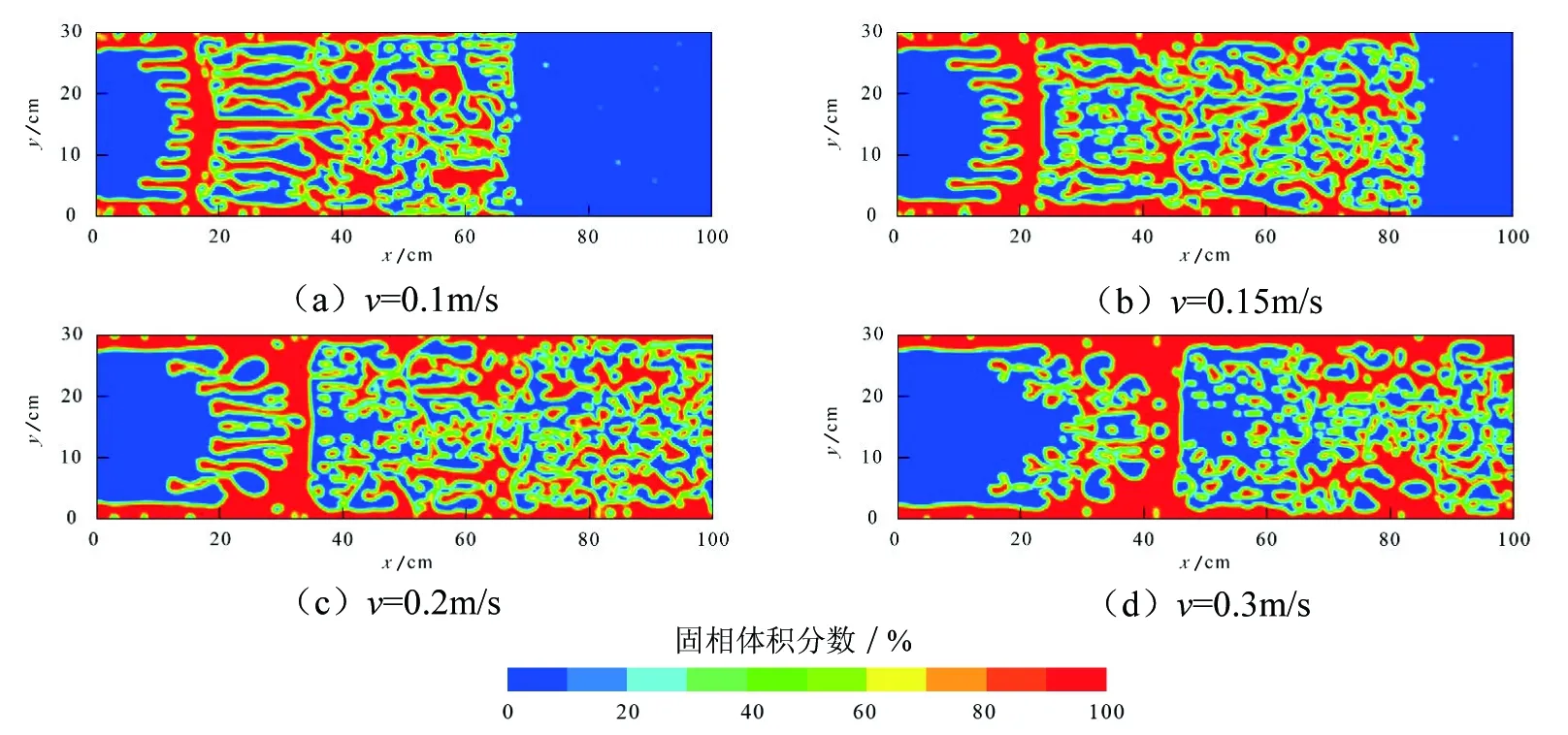
圖8 不同注入速度時的支撐劑鋪置形態

圖9 不同注入速度下的通道率分布

3.4脈沖間隔時間的影響

脈沖加砂壓裂通過特殊混砂設備切換支撐劑段塞和中頂液的交替注入，實現支撐劑段塞之間的分隔，是脈沖加砂壓裂區別于常規壓裂工藝的顯著特征，其中脈沖間隔時間即為中頂液注入時間，它是支撐劑簇團在縫內形成非均勻鋪置的基礎條件。保持黏度比R=5，注入速度v=0.15m/s，攜砂液注入時間Txs=30s不變，改變脈沖間隔時間Tjg分別為20、30、40、50s，總共注入周期仍為6個，不同脈沖間隔時間對支撐劑鋪置形態的影響及通道率的分布情況，如圖10和圖11所示。

從圖10和圖11可以看出，增大脈沖間隔時間，支撐劑有效鋪置距離和通道率增大，砂團分散效果變好，但過短或過長的脈沖間隔時間均不利于有效滲流通道的形成：脈沖間隔時間過短，前后兩個支撐劑段塞融合在一起無法形成大面積的滲流通道，且有效支撐縫長不足(圖10(a))；脈沖間隔時間過長，兩個支撐劑段塞之間的通道面積和無支撐劑區域過大(圖10(d))，容易導致該區域裂縫閉合。綜合考慮通道率和支撐劑簇團分散效果，當脈沖間隔時間為30～40s，即脈沖間隔時間為整個脈沖周期的0.5～0.6倍時，支撐劑有效鋪置距離較長且支撐劑分散較為均勻，以保證地層閉合壓力作用下支撐劑簇團的穩定支撐和高速滲流通道的有效開啟。

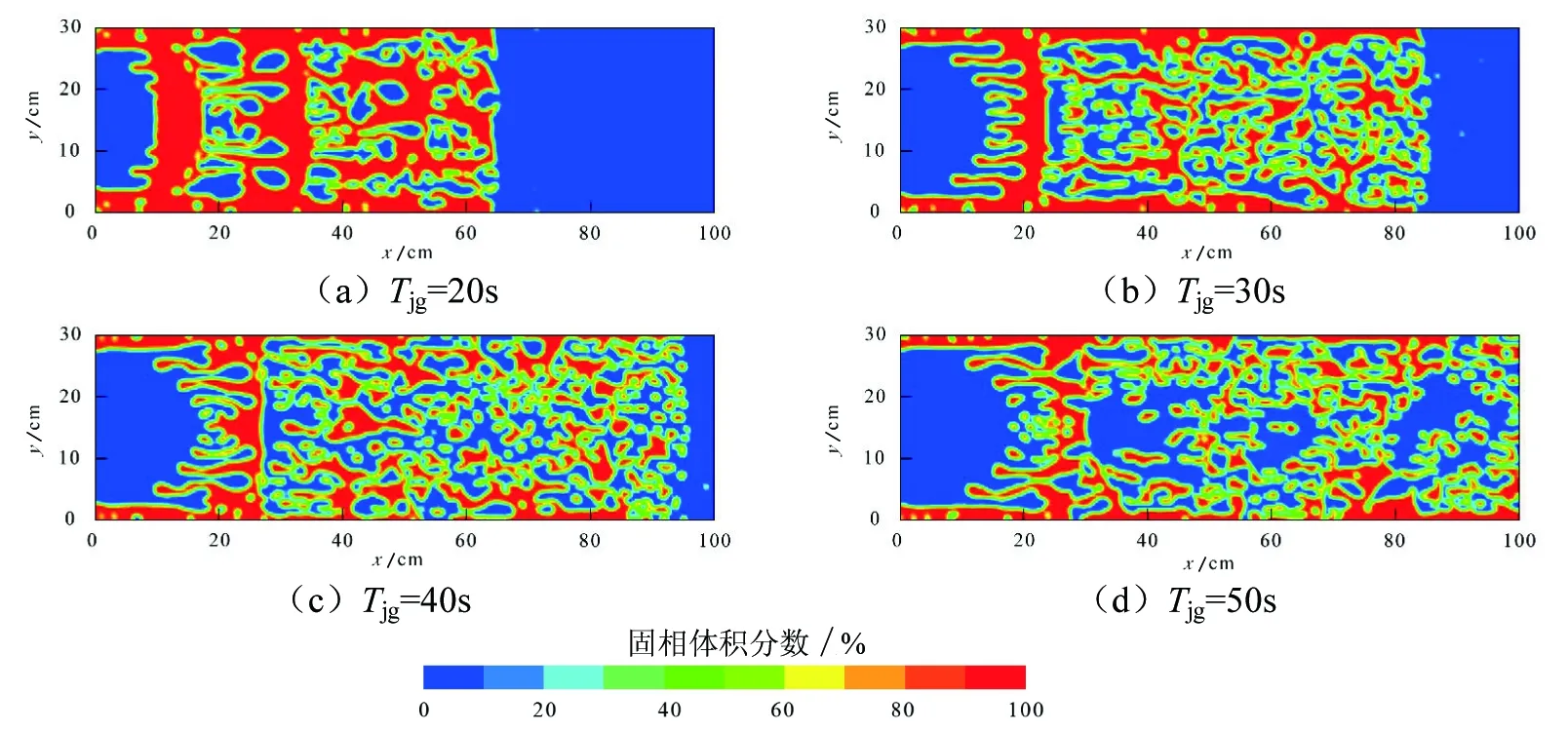
圖10 不同脈沖間隔時間的支撐劑鋪置形態

4 結論

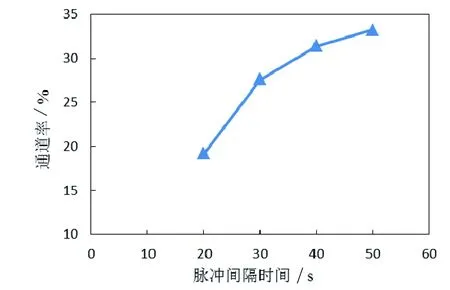
圖11 不同脈沖間隔時間下的通道率分布

1)對比數值模擬與實驗研究結果表明：歐拉雙流體模型能夠較為準確地捕捉脈沖加砂過程中支撐劑剖面形態的變化，數值模擬結果與物模實驗結果符合度較高。

2)攜砂液與中頂液黏度比對支撐劑的鋪置影響較大，不合理的黏度比會導致有效支撐縫長和通道率減小，支撐劑簇團分散效果變差，降低脈沖加砂壓裂改造效果，建議現場施工時黏度比不宜超過5。

3)注入速度增大，支撐劑有效鋪置距離和通道率增大，但支撐劑簇團分散效果變差，綜合考慮通道率和砂團分散效果，折算現場合理施工排量為3.2～4.3 m3/min。

4)過短或過長的脈沖間隔時間均不利于有效滲流通道的形成，脈沖間隔時間為整個脈沖周期的0.5～0.6倍時效果較好。

[1]戚斌，楊衍東，任山，等. 脈沖柱塞加砂壓裂新工藝及其在川西地區的先導試驗[J]. 天然氣工業，2015，35(1)：67～73.

[2] Brannon H D，Malone M R，Richards A R. Maximizing fracture conductivity with proppant partial monolayers：theoretical curiosity or highly productive reality[J]. SPE90698，2004.

[3]錢斌，尹叢彬，朱炬輝，等. 高效脈沖式加砂壓裂技術研究與實踐[J]. 天然氣工業，2015，35(5)：39～45.

[4] Tinsley J M, Williams J R. A new method for providing increased fracture conductivity and improving stimulation results[J].SPE-AIME 4676,1973.

[5] Parker M A, Glasbergen G, Batenburg D W, et al. High-porosity fractures yield high conductivity[J].SPE96848,2005.

[7] 吳順林，李憲文，張礦生，等. 一種實現裂縫高導流能力的脈沖加砂壓裂新方法[J]. 斷塊油氣田，2014，21(1)：110～113.

[8] 楊衍東，劉林，黃禹忠，等. 水平井脈沖柱塞加砂新技術在中江氣田的應用[J]. 石油與天然氣化工，2016，45(1)：67～72.

[9] 武生智，任春勇. 基于歐拉雙流體模型的風沙運動模擬[J]. 蘭州大學學報(自然科學版)，2012，48(1)：104～107.

[10]Benyahia S.On the effect of subgrid drag closures[J]. Industrial & Engineering Chemistry Research，2009，49(11)：5122～5131.

[11] Srivastava A，Sundaresan S. Analysis of a frictional kinetic model for gas-particle flow[J]. Powder Technology，2003，129(1)：72～85.

[12] Benyahia S，Syamlal M，O`Brien T J. Evaluation of boundary conditions used to model dilute，turbulent gas/solids flows in a pipe[J]. Powder Technology，2005，156(2)：62～72.

[13] 荊德吉，葛少成，劉劍. 基于歐拉-歐拉模型的落煤塔控塵技術研究[J]. 中國安全科學學報，2012，22(10)：126～132.

[編輯] 黃鸝

TE357.1

A

1673-1409(2017)19-0090-07

2017-04-18

國家科技重大專項(2016ZX05048)。

李凌川(1987-)，男，碩士，助理工程師，主要從事致密低滲儲層改造研究工作，lilc.hbsj@sinopec.com。

[引著格式]李凌川，張永春，李月麗.脈沖加砂壓裂支撐劑鋪置狀態的CFD模擬[J].長江大學學報(自科版), 2017,14(19):90～96.