海底子母管作用下海床沖刷的試驗研究*

潘新穎， 趙恩金， 拾 兵， 于 冬， 黃修筠

(中國海洋大學工程學院，山東 青島 266100)

海底子母管作用下海床沖刷的試驗研究*

潘新穎， 趙恩金， 拾 兵， 于 冬， 黃修筠

(中國海洋大學工程學院，山東 青島 266100)

子母管作為海洋工程中的新型管線結構，越來越受到重視。本文運用物理試驗的方法研究了穩定流中海底子母管對海床局部沖刷的影響。通過控制不同海底子母管間間距，管徑及來流流速，分析出了兩管間隙比對沖刷坑內沖刷深度的影響，同時，從泥沙起動原理出發，利用流體的連續性特征，推導了與子母管間間隙比、管徑及來流流速相關的沖刷坑深度理論公式，該理論公式與試驗結果吻合良好，可預測子母管下泥沙的沖刷。通過試驗可知，雷諾數及子母管間間隙對沖刷坑深度有較大的影響。在一定雷諾數下，子母管間間隙越小，沖刷坑深度越大，泥沙輸移越也越嚴重。在管線間間隙比不變時，雷諾數增加同樣能加強管線下方沖刷。

子母管線；沖刷深度；海流；沖刷機理；試驗研究

隨著海底管線的廣泛應用，子母管作為一種新的海底管線結構，能夠降低管道的設計和施工成本，提高海洋油氣田開發的經濟效益[1]。子母管的大(母)管用于輸送原油，小(子)管位于大管的正上方，用于輸送一些置換介質(柴油、海水)及控制信號等。子母管結構如圖1所示。D為母管直徑，d為子管直徑，G為兩管之間間隙。該管線結構已在渤海海域BZ34-3/5邊際油田中有所應用[2]。管線的存在極易造成下部泥沙的沖刷，造成管線懸空，甚至破壞，因此，對海底子母管下方泥沙沖刷研究極其重要。

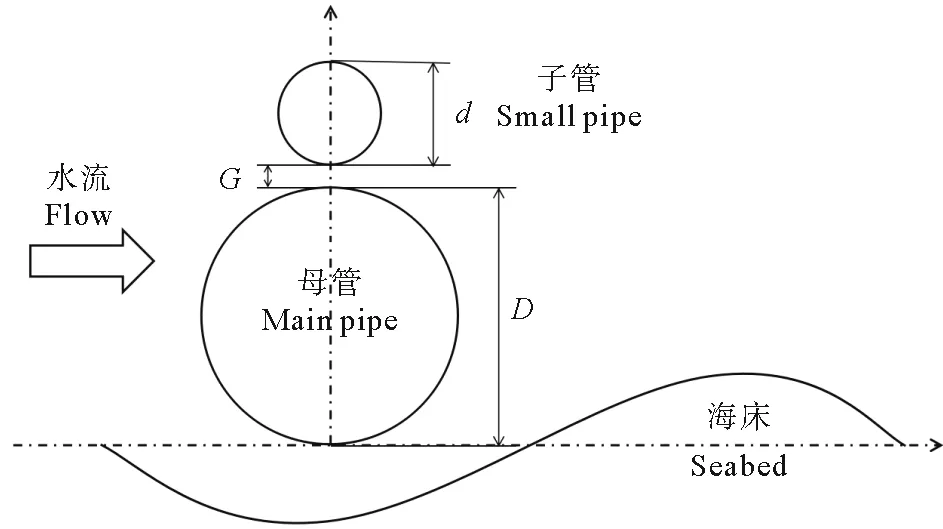
圖1 海底子母管的基本結構形式Fig.1 Sketch of submarine piggyback pipeline configuration

海底子母管的結構形式比單一管道的結構復雜，導致子母管周圍的水動力特性，流場形態及對海床沖刷影響更為復雜。

目前，國內外對“單一”結構形式管線下的海床局部沖刷已經進行了充分的研究。張芝永等人[3]基于N-S方程和有限體積法，在FLUENT中通過二次開發建立了近床面水平圓柱局部沖刷二維數值模型。劉勇等人[4]對單向恒定流作用下的海底管線沖刷坑內泥沙動水休止角進行了理論分析和試驗研究，得出了管線迎流面的動水休止角要略大于背流面的動水休止角并基本呈線性變化規律。Lipeng Yang等人[5]對安裝剛性導流板的管線下泥沙沖刷深度進行了計算及試驗，他指出雷諾數及導流板高度對沖刷坑深度都有很重要的影響。夏令[6]研究了波浪作用下的泥沙起動及海底管線周圍局部沖刷，通過物理試驗分析了沖刷發展的物理過程，測量了管道底部的沖刷深度，得到了無因次沖刷深度與KC數之間的一般規律。潘冬子通過波浪水槽實驗，研究波浪荷載引起的管線周圍局部沖刷機理和形態，探討了行進波作用下海床局部沖刷的演化規律及平衡沖刷深度與KC數的關系[7]。

然而，對子母管這種新型結構的研究多限制在子母管的水動力特性方面。崔金生等人[8]基于量綱分析的方法，通過模型試驗，研究了在穩定海流中子母管渦激振動的情況，指出子母管橫向渦激振動具有明顯的不對稱性。Kalghatgi S G等人[9]對作用在子母管上的水動力強度進行了分析，通過試驗指出由于子母管兩管的相互影響，作用在子母管上的拖曳力系數比單一結構管線增加50%～100%，對升力系數也有較明顯的影響。Zhao Ming等人[10]對恒定流中子母管下的局部沖刷進行了數值模擬，數值模型中兩管間的間隙比從0～0.5之間變化，通過分析發現沖刷剖面受間隙比的影響較大，但未對數值模擬結果進行物理驗證。馬良等人[11]以JZ20-2海底輸氣管道工程為背景，對JZ20-2的子母管在波流作用下水動力載荷的確定進行了試驗研究，分析了子母管水動力系數CD、CM與KC數對管線受力的影響。成小飛等人[12]對波流共同作用下海底子母管線水動力進行了物理模型試驗研究，基于Morison方程，采用“等效直徑法”分析了流速比Uc/Uw，母管與海床間隙比e/D及子母管間的相對縫隙G/D對海底子母管水動力系數的影響。

當海底子母管鋪設在海床面時，能夠加劇海床面的沖刷，沖刷坑深度增加，使管線產生滑移造成管線的破壞。之前對子母管的研究著重于管線的受力分析，對子母管下沖刷坑的延展過程研究的卻很少。本文通過物理試驗的方法，從理論及試驗兩方面對沖刷過程進行了分析，同時探討了兩管間不同的間隙比(e=G/D，G為兩管間間距，D為母管的直徑)，子母管管徑及來流流速對沖刷的影響，對海底子母管的穩定設計及合理鋪放具有非常重要的意義。

1 理論分析

1.1 泥沙起動原理

在恒定流中，管線的兩側存在著壓力差，管線前方壓力較大，管線尾跡區壓力較小，壓差使附近海床產生水力梯度，水力梯度越大，管線周圍海床泥沙的滲透力越大；當滲透力大于土體浮重并且合力方向向上時，海床便發生管涌，產生滲透破壞[13]。

海底子母管下床面泥沙起動，通過臨界希爾茲數確定，其希爾茲數的表達式為

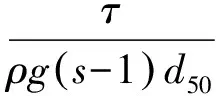
(1)

式中：τ為床面切應力；ρ為水的密度；g為重力加速度；s為泥沙比重；d50為泥沙中值粒徑。

海床面上泥沙起動臨界希爾茲數為：

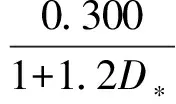
(2)

式中：D*=[g(s-1)/v2]1/2，為無量綱泥沙顆粒尺寸。

在有坡度的床面上泥沙臨界起動希爾茲數公式[14]，通過如下公式進行修正：

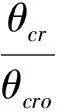
(3)

式中：α是管線沖刷后海床面與水平面的夾角，也稱坡角，規定上坡為正角，下坡為負角；φ為泥沙休止角。

產生滲透破壞的臨界水力梯度為：

icr=[(ρs/ρw)-1](1-ns)，

(4)

式中：ρs為泥沙密度；ρw為海水密度；ns為沙土孔隙率。

平均單寬體積輸沙率q0由下式求得

(5)

式中：s為泥沙比重；θ為泥沙床面希爾茲數；θcr為泥沙臨界起動希爾茲數；d50為泥沙中值粒徑。

推移質單寬輸沙率可表示為：

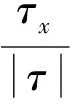
(6)

式中：q0為平面單寬體積輸沙率；τ為床面剪應力；τx為床面剪應力x方向分量；經驗系數C取值范圍為1.5～2.3[15]。

床面變形模型根據輸沙平衡規律，海床面高程變化h可用沖淤方程表示：

(7)

式中：p0為床沙孔隙率；qbx為x方向推移質單寬體積輸沙率。

1.2 海底子母管下方沖刷平衡后理論分析

沖刷平衡后，子母管線周圍流場及沖刷坑情況，如圖2所示。

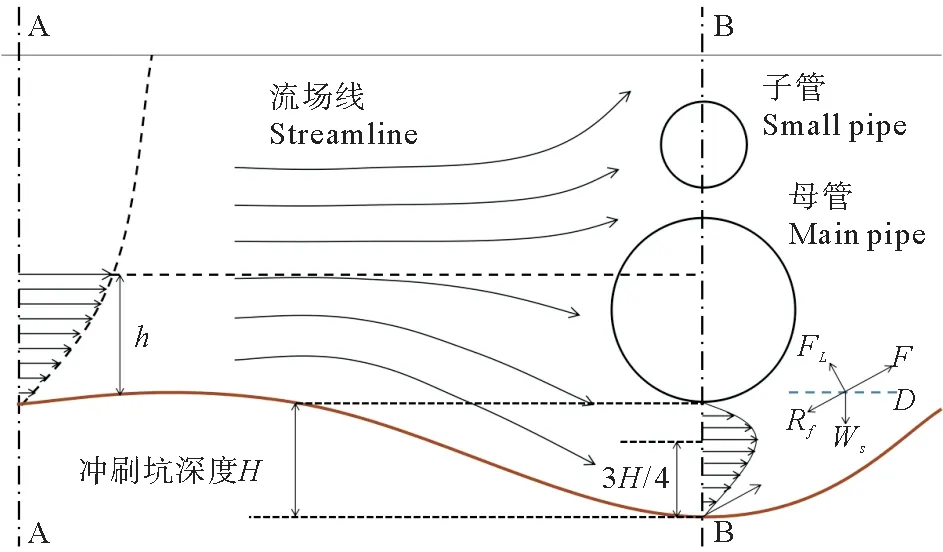
圖2 子母管周圍流速分布Fig.2 The velocity distribution around piggyback pipeline

沖刷穩定時，將沖刷坑最深點床面上，某高度處沿床面方向的流速定義為“沖止流速”。本文所討論的沖刷為清水沖刷，且上游無泥沙補給的情況，因此，沖刷穩定時坑內泥沙將處于靜止狀態，根據力學平衡原理，顆粒所受的升力FL、水下重力Ws、拖曳力FD及摩擦阻力Rf間存在著平衡關系[5]。由此得出，摩擦阻力與重力沿床面分力之和等于推移力，可推出沖止流速為：

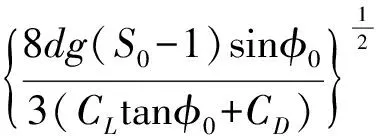
(8)

式中：S0為泥沙容重與水容重的比值(S0=(ρs/ρ)；ρs為泥沙顆粒的比重；ρs為水的比重；g為重力加速度；d為泥沙顆粒平均粒徑；φ0為泥沙的動水休止角，其受結構物影響，并隨管徑、子母管間隙比及來流流速的變化而變化；CL為升力系數，愛因斯坦根據埃爾-薩姆尼的試驗成果，發現距理論床面0.35d處的流速對應的CL為常數可取為0.178，CD為推移力系數，當試驗條件為紊流時可取0.45[16]。

根據之前研究發現[5]管道沖刷達到穩定后，沖刷坑內流速呈指數分布(見圖2)，因受床面和管道邊壁的共同影響，最大流速出現在距床面3hb/4處(hb為沖刷坑深度)，則沖刷坑底端至水平海床面3hb/4間的距離為y，流速u(y)可以表達為：

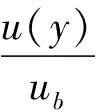
(9)

同時，3hb/4處至管壁處流速u′(y)可以表達為：

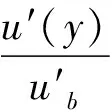
(10)

沖刷坑底部流速與沖刷坑底端至水平海床面3hb/4處的流速關系可用下式表示：

(11)

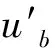
由于子管的存在，能夠增大子母管線整體的阻流受力面積，加劇下方海床面的沖刷及泥沙輸移，與單一結構管線相比沖刷坑寬度的幅度大于深度，因此子母管下的動水休止角比單一結構管線下動水休止角小。同時，因受床面和管道邊壁的共同影響，根據Yang等人及本試驗結果發現沖刷坑內最大流速在沖刷坑最低端到正常海床面深度的3/4處，管道迎流面上駐點的高度隨子管與母管之間的間隙G的不同及管徑的變化(母管管徑為D，子管管徑為d)而變化，其表達式為h=(D+de-G)/2。

斷面A-A上床面至h處的流速分布可寫為：

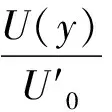
(12)

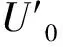
(13)

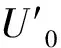
利用流體連續性條件，則有：

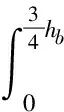
(14)

將式(9)～(13)帶入式(14)中，得出子母管下沖刷坑深度的計算公式為：

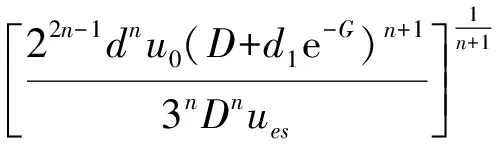
(15)

2 物理試驗及分析

本試驗在中國海洋大學工程學院河流工程實驗室波流環形水槽中進行的，試驗物理模型如圖3所示。

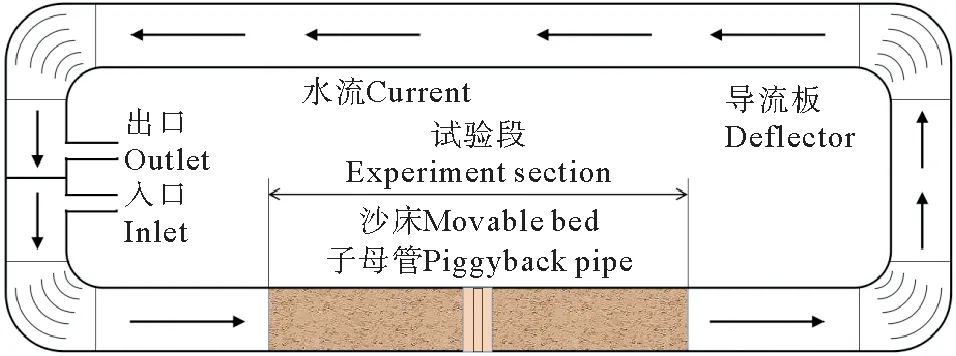
圖3 物理試驗裝置Fig.3 Experiment arrangement

水槽長25.0 m，寬0.5 m，深0.6 m，水槽中央填有非均勻沙，用來模擬沙質海床，沙床高0.15 m，長5.0 m。

2.1 試驗參數及步驟

試驗主要測量了子母管與床面無間隙比時，不同管徑、流速及兩管間間隙比對沖刷坑內的流速分布、沖刷深度的影響。管道模型長度為0.5 m，母管外徑分別為0.08、0.10、0.12 m，根據工程實際運用[2]，子母管徑比一般為0.358，對應的子管外徑分別為0.03、0.035、0.04 m。試驗中子母管間隙比分別設置為0、0.25、0.5。試驗水溫為15℃，運動黏滯系數為1.120 1×10-6m/s2。試驗水深為Ho=0.4 m，管道上游距床面D/2高度處的來流流速分別為0.24、0.3、0.4 m/s，泥沙中值粒徑d50為0.3 mm，孔隙率n為0.4。試驗工況及參數如表1所示。

試驗值的獲取主要集中在動床上，管道上游、管道迎流面及沖刷坑內的流場分布采用ADV(Acoustic Doppler Velocimeter)進行測量，測量精度為±1 mm。試驗所用ADV探頭為側向的，測量的是其側方5 cm處的流速，對測點影響較小，通過流場的試驗值可以確定管道上游駐點的高度及流速分布指數。本文中的駐點高度即：管道迎流面上流速為零的點與床面間的高度，其可由管道迎流面的斷面流速分布確定。沖刷穩定后，將水槽內水完全排出，采用精度為0.1 mm的測針對沖刷坑的斷面進行測量，ADV及測針均垂直固定于水槽上方的數據采集車上，其可沿水槽自由運動，方便取值。

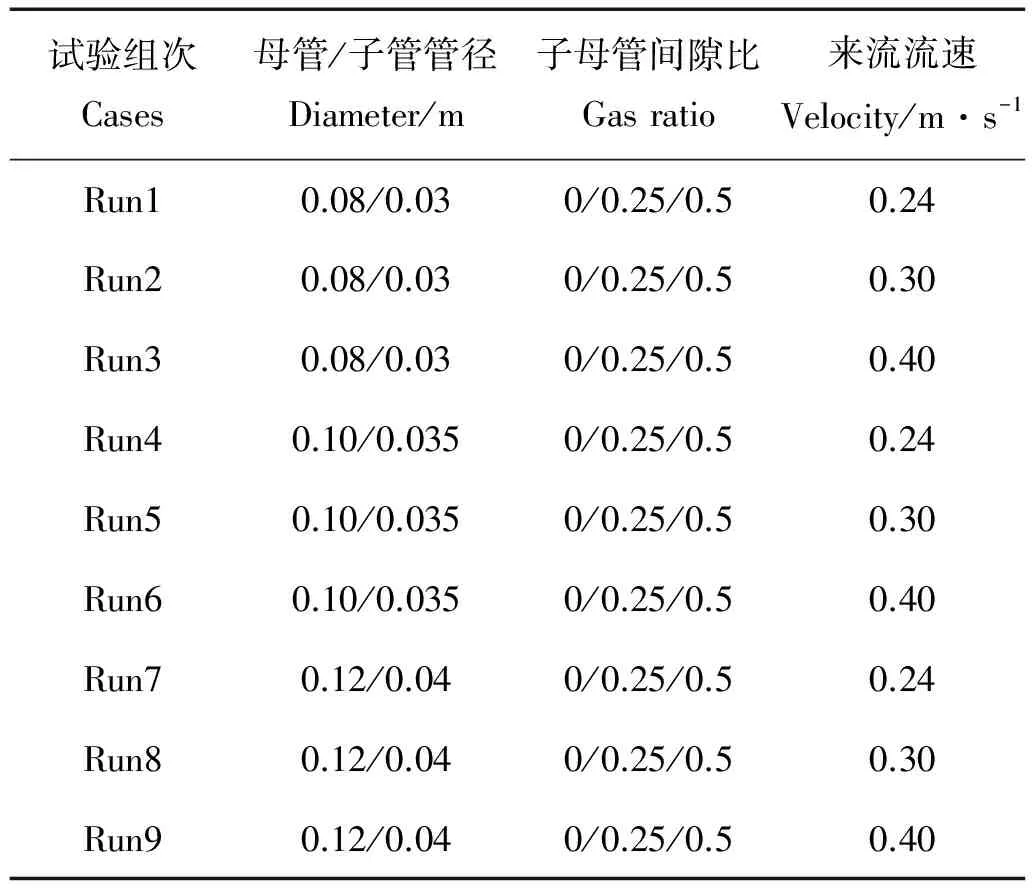
表1 試驗工況及參數Table 1 Experiment cases and parameters

2.2 試驗結果分析

2.2.1 沖刷現象描述 當水流速度增加到一定值時，管線下方的泥沙滲透力大于泥沙顆粒重力，海床開始出現管涌現象，隨著時間和流速的增大，管道底部海床出現一處或幾處泥沙輸移后產生沖刷間隙，同時，間隙沿著管道軸線方向發展并形成一個沖刷坑。管道懸空主要是由于管線兩側的壓力差使沙床內產生滲透力造成泥沙輸移[17-19]。當子母管與沙床間的間隙很小時，間隙內的流速是來流流速的數倍，增大了床面的剪切力，造成輸沙率增加。當沖刷坑深度及寬度達到一定值后，床面的沖刷坑形態基本不再發生變化，此時，為平衡沖刷階段，不再出現泥沙輸移的情況。

2.2.2 沖刷結果分析 沖刷穩定后沖刷坑的狀態取決于子母管管徑、子母管管間隙及來流流速，圖4給出了不同流速下沖刷坑的幾種形態。

在試驗中，試驗管線采用有機透明玻璃管，為了能看清子母管及沖刷狀態，在管內設置了白色泡沫板，而管壁仍為透明狀態并且存在一定厚度，因此，在拍攝照片，間隙為0時，如同存在間隙，而試驗時兩管間并未有間隙存在。試驗結果顯示：在相同子母管管徑及間隙比下，管道下方沖刷坑的深度及寬度隨來流流速的增加顯著增大，如圖4(a)，(b)所示。在相同來流流速及相同管徑下，沖刷坑的深度及寬度隨著子母管間間隙的增大而減小，如圖4(a)，(c)，(e)所示。在相同情況下，沖刷坑的深度及寬度隨著管徑的增大而增加，并且沖刷坑的最深點出現向下游偏移的趨勢。動水休止角與沖止流速和沖刷坑深度的變化規律相反，隨著子母管間間隙及流速的增大而減小，并且最終趨于穩定。通過照片對比可知，子母管間間隙對沖刷坑有較大影響，間隙比越小，泥沙沖刷的越劇烈，泥沙輸移程度越明顯。

圖4 不同流速及間隙比下沖刷坑狀態(D=0.01m)Fig.4 Experimental photos of the scour around the piggyback pipe for D=10cm

2.2.3 公式參數的確定 通過擬合試驗數據的方法確定沖刷坑深度公式中的參數。圖5為泥沙休止角與沙粒雷諾數的關系曲線。

通過分析試驗數據發現，當管線為單一結構及管線與沙床面無間隙時，休止角φ0是僅與沙粒雷諾數有關的系數，沙粒雷諾數定義為Re*=u*ds/v(u*為摩阻流速)。通過試驗數據擬合，得到其關系式為：

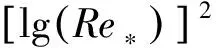
(16)

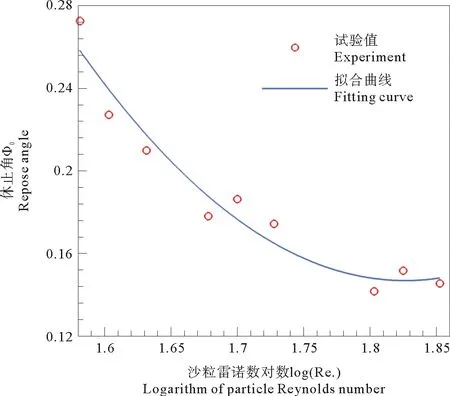
圖5 休止角φ0與lg(Re*)的關系式擬合曲線Fig.5 The relationship curve of repose angle and lg(Re*)

當管道為子母管且管線與沙床無間隙時，休止角φ是與子母管間間隙、沙粒雷諾數及管徑有關的參數。通過數據分析發現φ可由φ0及系數k表示。其表達式可寫為φ/φ0=k=f(G/D)，G為兩管間間隙比，D為母管管徑，其中，當G趨近于無窮時，相當于單一管線結構狀態。擬合曲線如圖6所示，則k的關系表達式可寫為：

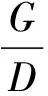
(17)

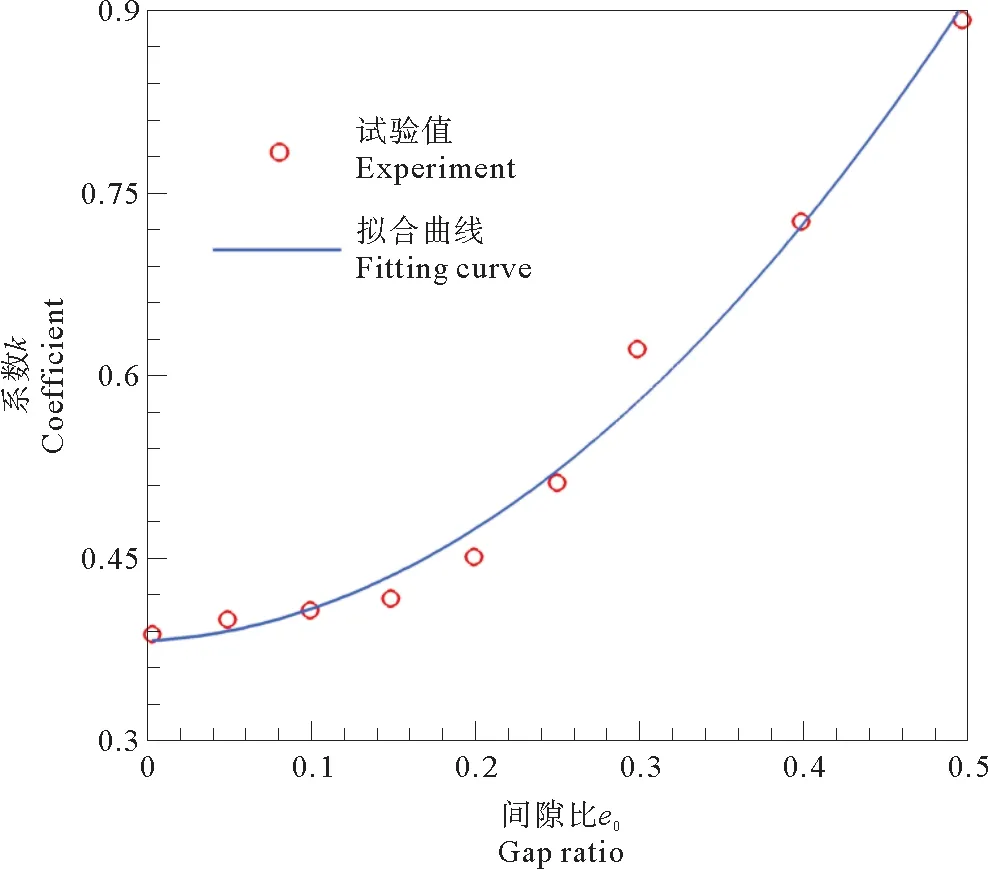
圖6 系數k與G/D的關系曲線Fig.6 The relationship curve between k and G/D

指數n是由試驗測定的流場數據確定的。試驗發現在一定不同條件下(如：相同的子母管間間隙比和管徑)，不同來流流速的流場分布規律呈現相同趨勢。在此，以圖7為例闡述指數的確定方法。圖7為子母管線沖刷穩定后，沖刷坑內流速隨豎直高度y的變化曲線，y為沖刷坑內距床面的豎直高度；H為水深，u為坑內不同高度處對應的流速。通過圖7可知，當流速u0=0.24 m/s時，指數n為1/6時，試驗值和擬合曲線吻合良好，當流速u0=0.30 m/s時，指數n為1/4時，兩者吻合良好，并且來流流速越小，高度比相對于流速比變化越明顯。

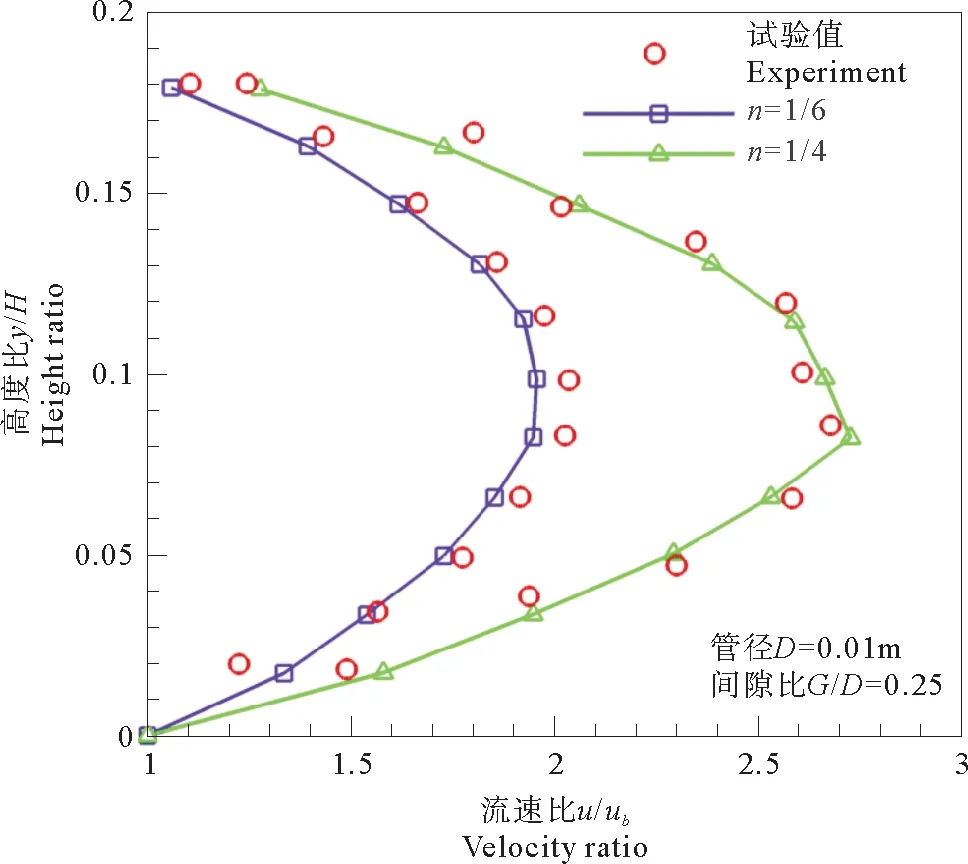
圖7 不同流速時沖刷坑內流速分布指數nFig.7 The distribution index n in the scour hole

2.3 沖刷坑深度對比

在單一管線及與海床面無間隙的條件下，沖刷深度的計算值中即不存在子管與子母管間間隙，即式中的間隙距離G趨近于無窮，計算值與試驗值的對比曲線如圖8所示。對于同一管徑，深度隨流速的增加而增大；對于同一試驗條件(如來流流速)，深度隨管徑的增大而增大。并且Mao[20]的試驗數據也用來驗證計算公式，結果顯示：計算值與試驗值相近，公式能反映試驗數據的變化規律。

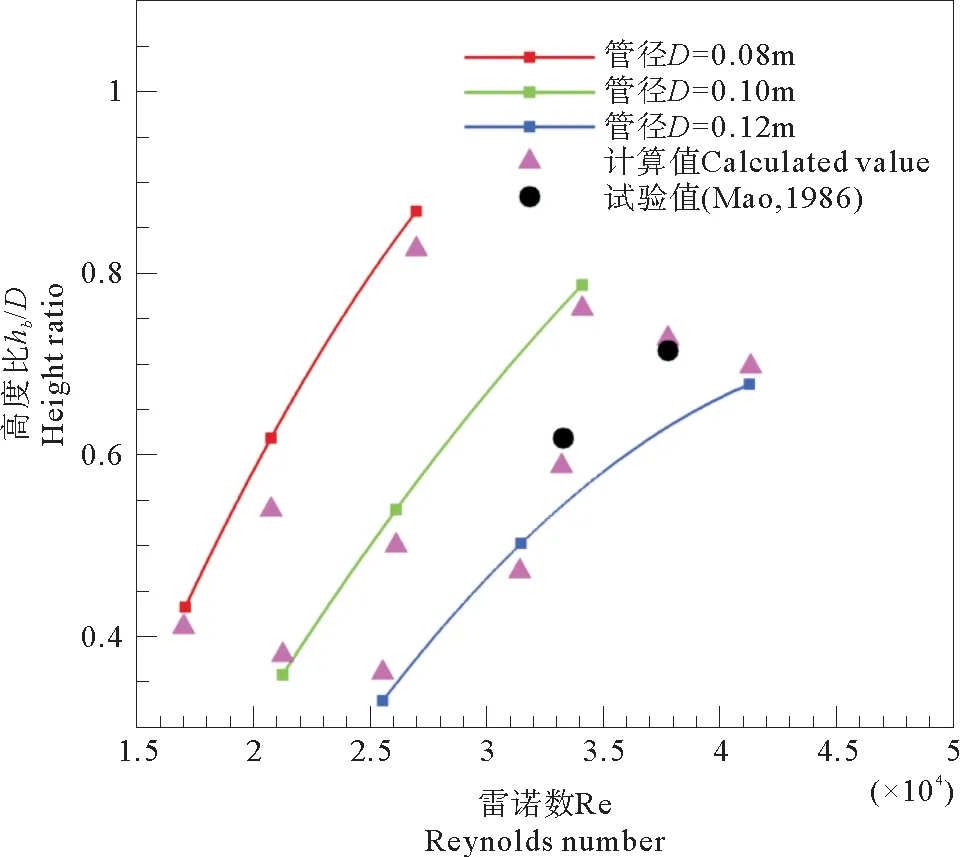
圖8 無間隙單一管線計算值與試驗值對比曲線Fig.8 The comparison between calculated data and test values

下圖為子母管線兩管間不同間隙比時，沖刷坑的深度計算值與試驗值的對比曲線。由圖9可知，沖刷坑深度隨著間隙比的減小而增大，隨著雷諾數的增加而增大；同一雷諾數條件下，間隙比為0時沖刷坑深度遠遠大于間隙比為0.5時的沖刷坑深度，來流流速越大這種趨勢越明顯。

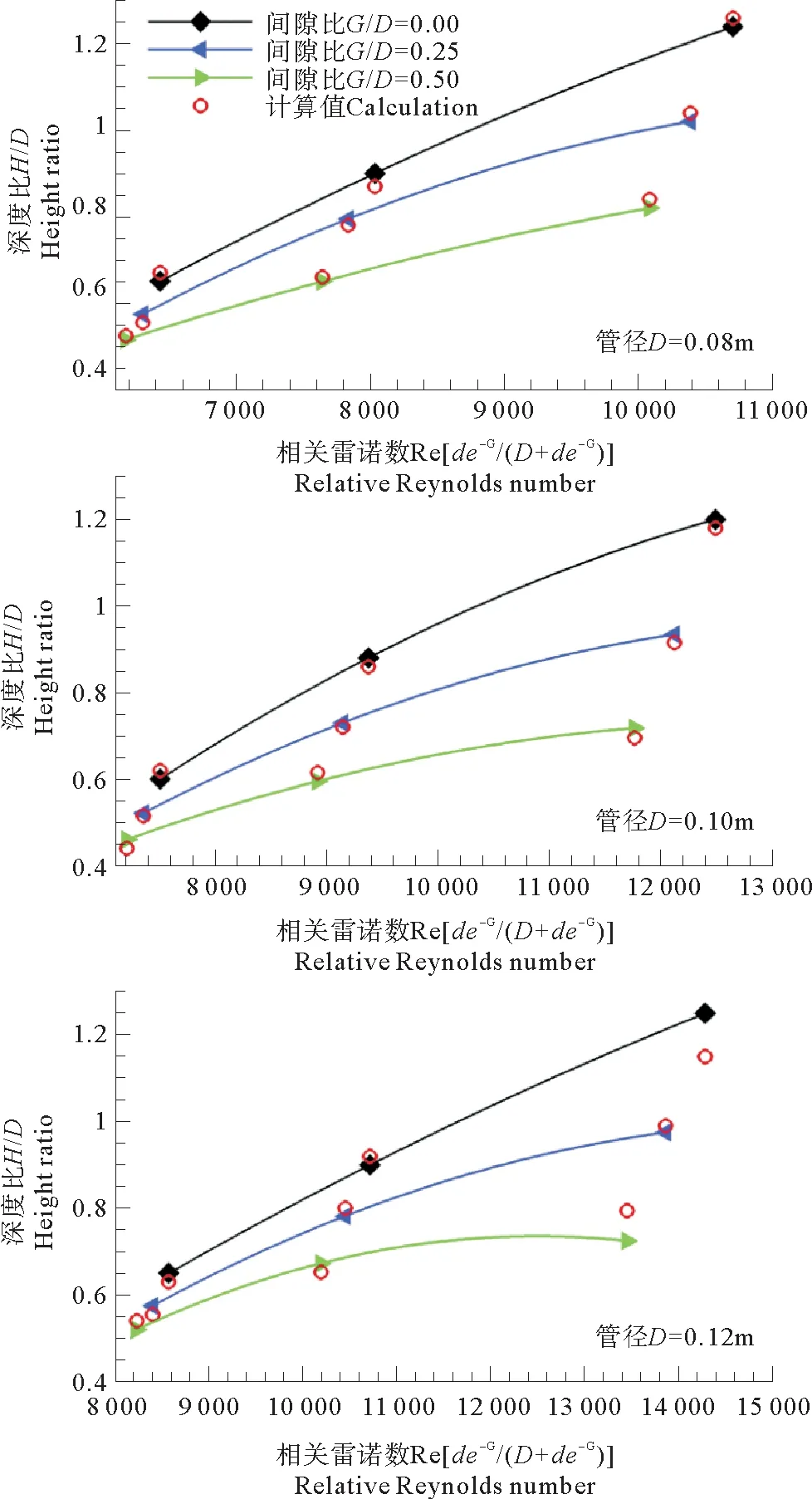
圖9 不同條件下沖刷坑計算值與試驗值的對比曲線Fig.9 Comparison of calculated values and test data

子母管管徑對沖刷坑深度也有很大影響，在相同雷諾數條件下，隨著管徑的增加，沖刷坑深度與管徑之比的比值越小。同時，對比單一結構管線下沖刷坑深度明顯增加。Chiew[21]獲得的兩組試驗值也用于驗證公式的合理性，結果顯示試驗值與計算值吻合良好。但也出現了個別點相差較大，筆者認為在試驗過程中，流速增加，紊動作用較大出現泥沙沖刷不均勻現象和系統誤差造成的。

3 結論

本文研究了子母管不同管徑、不同管間間隙、不同流速條件下沖刷坑內泥沙起動、流速分布及沖止流速的情況，在此基礎上，討論了沖刷坑內沖刷深度以及休止角的變化，得出結論如下：

(1)通過試驗分析出了不同條件下沖刷坑的變化情況，沖刷坑狀態與子母管不同管徑，管間間隙及來流流速都有密切的關系，管徑越大，間隙越小及來流流速越大，沖刷坑深度越大。

(2)通過不同條件下沖刷對比，得出動水休止角與沖止流速的規律與沖刷坑深度的變化規律相反，隨著子母管間間隙及流速的增大而減小。

(3)采用流體的連續性條件，推導了子母管下沖刷穩定時不同試驗條件下的沖刷深度計算公式。流速的分布和沖止流速是決定沖刷坑深度的主要因素，該深度與兩管間間隙比有直接關系，間隙比越小，沖刷坑深度越大。經試驗值與計算值的對比分析，充分驗證了該沖刷坑深度計算公式。

不足之處，本文并沒有研究子母管與床面存在間隙的情況及該間隙對沖刷坑的影響程度。

[1] Brockbank J. Bundled pipes speed offshore laying[J]. Oil and Gas Journal, 1990, 88(19): 78-84.

[2] 楊玻, 倪浩, 朱曉環. 一種新型的置換海底子母管道技術[J]. 中國造船, 2007, 48: 563-570. Yang H, Ni H, Zhu X H. An Applicable Replacement Bundled Pipeline Structure for Offshore Marginal Oilfield Development[J]. Shipbuilding of China, 2007, 48: 563-570.

[3] 張芝永, 拾兵, 范菲菲, 等. 近床面水平圓柱局部沖刷二維數值模擬[J]. 計算力學學報, 2012, 29(5): 759-764. Zhang Z Y, Shi B, Fan F F, et al. Two-dimensional numerical simulation of local scour around horizontal cylinder near sand bed[J]. Chinese Journal of Computational Mechanics, 2012, 29(5): 759-764.

[4] 劉勇, 拾兵, 楊立鵬, 等. 海底管線作用下的泥沙休止角的試驗研究[J]. 海洋湖沼通報, 2012, 4: 31-35. Liu Y, Shi B, Yang L P, et al. Experimental study on the angle of repose of sediment under the action of submarine pipeline[J]. Transactions of Oceanology and Limnology, 2012, 4: 31-35.

[5] Yang L P, Shi B, Guo Y K, et al. Calculation and experiment on scour depth for submarine pipeline with a spoiler[J]. Ocean Engineering, 2012, 55: 191-198.

[6] 夏令. 波浪作用下的泥沙起動及海底管線周圍局部沖刷[D]. 浙江: 浙江大學, 2006. Xia L. Study on the Sediment Onset and Local Scour Around Submarine Pipeline Under the Action of Wave[D]. Zhejiang: Zhe Jiang University. 2006.

[7] 潘冬子, 王立忠, 潘存鴻, 等. 推進波作用下海底管線周圍局部沖刷實驗研究[J]. 海洋工程, 2007, 25(4): 27-35. Pan D Z, Wang L Z, Pan C H, et al. Local scour around pipeline due to progressive wave[J]. The Ocean Engineering, 2007, 25(4): 27-35.

[8] 崔金聲, 高福平, 韓希霆, 臧志鵬. 海流作用下子母管結構橫向渦激振動[J]. 海洋工程, 2012, 30(1): 18-24. Cui J S, Gao F P, Han X T, et al. Vortex-induced transverse vibration of piggyback pipelines in steady current[J]. The Ocean Engineering, 2012, 30(1): 18-24.

[9] Kalghatgi S G, Sayer P G. Hydrodynamic Forces on Piggyback Pipeline Configurations[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1997, 123: 16-22.

[10] Zhao M, Cheng L. Numerical Modeling of Local Scour below a Piggyback Pipeline in Currents[J]. Journal of Hydraulic Engineering, 2008, 134: 1452-1463.

[11] 馬良, 王金英, 孫紹述, 等. 海底(子-母)管道在波流作用下水動力載荷的實驗研究[J]. 大連大學學報, 1993, 3(4): 54-63. Ma L, Wang J Y, Sun S S, et al. Experimental Study of Hydrodynamic Force Loading under the Action of Wave Current on Submarine Composite Pipelines[J]. Journal of Dalian University, 1993, 3(4): 54-63.

[12] 成小飛, 王永學, 王國玉. 波流共同作用下海底子母管線水動力的物理模型試驗研究[J]. 海洋學報, 2012, 34(4): 172-180. Cheng X F, Wang Y X, Wang G Y. Physical model experimental study of hydrodynamic forces on submarine piggyback pipeline under waver-current coexisting action[J]. Acta Oceanology Sinica, 2012, 34(4): 172-180.

[13] 谷凡, 周晶, 黃承逵, 等. 海底管線局部沖刷機理研究綜述[J]. 海洋通報, 2009, 28(5): 110-120. Gu F, Zhou J, Huang C K, et al. Research on mechanism of local scour around submarine pipeline[J]. Marine Science Bulletin, 2009, 28(5): 110-120.

[14] Allen J R L. Simple models for the shape and symmetry of tidal sand waves: statically stable equilibrium forms[J]. Marine Geology, 1982, 48(12): 31-49.

[15] Br?rs B. Numerical modeling of flow and scour at pipeline[J]. Journal of Hydraulic Engineering, 1999, 125(5): 511-523.

[16] 邵學軍, 王興奎. 河流動力學概論[M]. 北京: 清華大學出版社, 2005. Shao X J, Wang X K. Introduction to River Mechanics[M]. Beijing: Tsinghua University Press, 2005.

[17] Cheng L, Chiew Y W. Modeling of flow around a near-bed pipeline with a spoiler[J]. Ocean Engineering, 2003, 30: 1595-1611.

[18] Zhao J, Wang X. CFD Numerical simulation of the submarine pipeline with a spoiler[J]. Journal of offshore mechanics and arctic engineering, 2009, 131(3): 031601-1-031601-5.

[19] 楊兵, 高福平, 吳應湘, 等. 海流引起海底管道懸空的數值模擬[J]. 中國造船, 2005, 46(增刊): 22l-226. Yang B, Gao F P, Wu Y X, et al. Numerical study of the occurrence of pipeline spanning under the influence of steady current[J]. Shipbuilding of China, 2005, 46: 22l-226.

[20] Mao Y. The interaction between a pipeline and an erodible bed[D]. Denmark: The Technology University of Denmark, 1986.

[21] Chiew Y M. Mechanics of local scour around submarine pipelines [J]. Journal of Hydraulic Engineering, 1990, 116(4): 515-529.

Abstract: As an important part of ocean engineering, the submarine pipeline has many advantages when it transports crude oil, such as low coast, safety, quick and convenient. However, with the development of pipeline technology, the normal pipeline can not be satisfied to the various need. Based on the normal pipeline, a new pipeline which is piggyback pipeline is paid more and more attention. As a new type of submarine pipeline, piggyback pipeline has been gradually adopted in engineering practice to enhance the performances and safety of the submarine pipelines. In this paper, according to the present research of normal pipeline, the influence of piggyback pipeline on the local scour is studied based on the experiment and theory analysis. At first, the theory of scour around piggyback pipeline is analyzed. The erosion-stop velocity is deduced firstly. When the scour obtains equilibrium, depending on the force balance, the scour depth calculated formulas around piggyback pipeline are derived due to the erosion-stop velocity and the continuity equation of flow in the pipeline interface. Secondly, the experiment is carried out in an annular flume which can produce the steady flow. Through the experiment, it is found that the main influence factors on the scour are pipeline diameters, gap-ratio and incoming flow velocity. The results show that at a define Reynolds number, the depth of scour hole increases with the decreasing of gap between the main pipe and small pipeline. However, when the gap does not change, the scour depth also increases with the increment of Reynolds number. When the pipe diameter increases, the scour depth under the pipeline is also increase. However, the ratio of scour depth to pipeline diameter decreases slightly. Finally, the calculation values and experimental data are compared. Through the comparison, the calculated values of formulas is well agree with the experimental data and the the accuracy of the formulas is verified. The feasibility of the proposed formula has been well calibrated by both experimental data. The findings drawn from this study are believed to be instructive in the future design and application of the piggyback pipeline.

Key words: piggyback pipeline; scour depth; current; scour mechanism; experiment

責任編輯 陳呈超

Experimental Study on the Local Scour Around the Piggyback Pipeline

PAN Xin-Ying, ZHAO En-Jin, SHI Bing, YU Dong, Huang Xiu-Yun

(College of Engineering, Ocean University of China, Qingdao 266100, China)

P751

A

1672-5174(2017)11-109-08

10.16441/j.cnki.hdxb.20150184

潘新穎， 趙恩金， 拾兵， 等. 海底子母管作用下海床沖刷的試驗研究[J]. 中國海洋大學學報(自然科學版), 2017, 47(11): 109-116.

PAN Xin-Ying, ZHAO En-Jin, SHI Bing, et al. Experimental study on the local scour around the piggyback pipeline[J]. Periodical of Ocean University of China, 2017, 47(11): 109-116.

國家自然科學基金項目(51279189)資助 Supported by the National Natural Science Foundation of China (51279189)

2015-04-11；

2016-02-12

潘新穎(1976-)，女，講師，主要從事海岸及海洋結構動力環境研究。E-mail: xinying@ouc.edu.cn