基于分層的FCM算法在醫學圖像分割中的應用*
孫玉娟, 王增鋒, 張小峰
(魯東大學信息與電氣工程學院, 山東 煙臺 264025)
基于分層的FCM算法在醫學圖像分割中的應用*
孫玉娟, 王增鋒, 張小峰
(魯東大學信息與電氣工程學院, 山東 煙臺 264025)
圖像分割是醫學圖像處理的關鍵問題和核心技術,醫學圖像中部分容積效應(PVE)、強度不一致(IIH)等現象的存在使該問題更為困難。作為有效處理PVE現象的FCM算法,在運行效率上面臨著很大挑戰。本文提出了一種基于分層的FCM算法,其核心思想是假設醫學組織器官的聚類中心僅僅取決于隸屬該組織器官的像素,而與隸屬于其他組織器官的像素無關。通過這樣處理,不僅可以保證較好的分割效果,從一定程度上改善強度不一致現象,同時可以提高算法的運行效率。在不同醫學圖像上的分割結果驗證了算法的有效性與可靠性。
分層FCM;圖像分割;醫學圖像處理
醫學圖像分割是從醫學圖像中提取感興趣的器官或特殊組織,是醫學圖像處理中的重要問題和核心技術[1]。對醫學圖像進行精確分割,是對病變組織進行定性及定量分析不可缺少的手段,同時又是進行三維重建等影像處理的基礎,分割的效果直接影響到三維重建模型的精確性,而面對CT、MRI、數字胃腸和數字減影等設備提供的千萬像素的影像數據和數以百計的斷面,要靠手工完成分割這項工作是不可能的。數十年來,眾多學者和科研人員就影像數據分割做了大量的研究工作,并取得了豐富的成果,但要實現正確、快速分割還有很長的路要走。如何提高影像分割的精度和速度仍然是目前公認的瓶頸。
當前,醫學圖像處理主要面臨三方面的問題:強度不一致(Intensity inhomogeneity,IIH)、部分容積效應(Partial volume effect,PVE)和噪聲[2-3]。對于圖像中存在的噪聲數據,通常采用濾波等方式進行去除[4-5];強度不一致現象是指隸屬于某一組織或器官的像素強度值不同,針對這個問題,眾多學者已經進行了大量的研究工作,通常采用的方式是在進行圖像處理前進行強度修正,然后對醫學圖像進行預處理[6]。部分容積效應現象指的是像素的強度值是鄰近醫學組織的強度均值,而并不是某一具體器官或組織的強度值,因此模糊聚類算法(Fuzzy C-Means,FCM)是處理PVE現象的有效算法[1]。遺憾的是,FCM算法在進行圖像分割時有以下主要問題:(1)像素的隸屬度采用隨機化的初始化方案,經常使分割后的效果集中在圖像的細節部分,忽略了圖像的主要部分;(2)運行過程中產生的聚類中心并不是圖像中真實存在的,這導致在目標函數最小化的過程中,算法的運行效率低下。針對上述問題,本文在深入研究的基礎上,提出了一種基于分層的FCM策略用于醫學圖像分割。
1 相關算法
作為一種無監督技術,FCM算法已經在數據挖掘、模式識別等相關領域得到了較為成功的應用[7-9]。在用于圖像分割時,其本質是為每個像素設置一個隸屬度,通過最小化目標函數優化隸屬度,最終達到圖像分割的目的。從本質上看,FCM算法是用軟分割方式替代硬分割,以從原圖像中保留盡可能多的信息。然而,在經典FCM算法中,像素的鄰域信息并沒有得到充分利用,并且算法的運行效率較為低下。針對這些問題,眾多學者和研究人員提出了諸如FCMS、EnFCM等相關改進算法,本部分將對FCM算法及其經典改進算法進行簡要介紹。
1.1 傳統的FCM算法
傳統的FCM算法通過迭代的方式對目標函數進行最小化,目標函數定義如下:
(1)

(2)

(3)
1.2 基于空間信息的FCM(FCMS)
針對FCM算法未利用鄰域信息這一缺點,Ahmed提出了一種改進的FCM算法——FCMS[10],在該算法中,每一像素的分類受其鄰域像素的影響。同樣,目標函數、隸屬度和聚類中心也應做相應的修正,其中目標函數如下定義:
(4)
其中:Nj是第j個像素的鄰域;NR是鄰域Nj中包含的像素數目;α是像素鄰域對中心像素的影響因子。類似,可以構造類似(2)式的拉格朗日方程,如下:
(5)


(6)


(7)
算法FCMS的執行過程與FCM的執行過程類似。由于考慮了鄰域信息的影響,FCMS在圖像分割中取得了比FCM較好的效果,且從一定程度上增強了對噪聲的魯棒性。然而,FCMS有兩個明顯的缺點:(1)由于在每一次迭代過程中均考慮鄰域信息,因此FCMS的效率仍然比較低。基于此,文獻[11]提出了FCMS1和FCMS2,用以提高算法的執行效率。(2)考慮了鄰域信息后將使目標函數在迭代過程中產生振蕩,導致函數的收斂性不好。因此在圖像分割中,FCMS算法需要預設的迭代次數要大于傳統的FCM預設的迭代次數。
1.3 EnFCM
為了提高FCM算法的效率,Szilágyi基于圖像的統計信息提出了EnFCM算法[12]。 算法首先基于下式對給定圖像進行濾波,得到第k個像素的灰度值:
(8)

(9)


(10)
(11)
與其他FCM改進算法相比,EnFCM的最大優勢是有效利用了圖像的統計信息,大大地加快了目標函數的優化速度,而這一點卻被其他FCM系列算法所忽略。雖然EnFCM是FCM系列算法中效率最快的,但在醫學圖像分割中,其分割效果卻也是最差的。實驗選取一幅醫學圖像,運用傳統的FCM以及FCMS和EnFCM分割效果如圖1所示。
從圖1可以看出:從分割效果上看,傳統的FCM算法和FCMS算法在圖像的細節分割效果比較令人滿意,但忽略了圖像的主要部分(胸腔外側的肌肉組織和脂肪韌帶軟組織),而EnFCM算法的分割效果從整體上不能令人滿意;從算法的執行時間上看,以512×512的醫學圖像為例,FCM以及FCMS的運行時間需要3 min左右的時間,而EnFCM卻可以在1 s以內完成圖像的分割。

圖1 醫學圖像以及相關分割結果Fig.1 The input medical image and the segmentation results
除了上述幾種主要的改進算法外,眾多學者還從其他方面對FCM算法進行了改進。如文獻[13-14]等基于鄰域信息和局部信息對FCM算法進行了改進,取得了一定的效果。文獻[15]將核函數與FCM算法進行有機結合,通過核函數將樣本空間映射至其他特征空間中,然后運用FCM算法,這在一些特定的問題中取得了一定的效果。文獻[16]將粒子群優化算法(PSO)應用到FCM算法中,提出了一種基于馬氏距離的PCM算法用于圖像分割。文獻[17]將傳統FCM算法中的歐氏距離表示成特征空間中的超正切函數,在胸部MR圖像的分割中取得了較好的效果。
與經典的FCM算法相比,相關改進算法的目標函數越來越復雜,雖然迭代次數有明顯減少,但每一次迭代的時間明顯延長,在某些改進算法中,每次迭代甚至達到了1 h以上[18],根本無法滿足圖像分割的實時性要求。因此,如何將FCM、FCMS與EnFCM的優點結合起來用于圖像分割,一直是眾多研究者的研究熱點,這也是本文研究的出發點。
2 基于分層的FCM算法
在FCM算法中,由于計算所得到的聚類中心并不是圖像中真實存在的點,這導致了目標函數在最小化的過程中收斂速度慢,從而導致了FCM算法較低的運行效率。同時會產生圖1(b)中無法分割出圖像主要成分的情況。本文認為,出現上述兩種情況的主要原因有兩個:(1)FCM算法在初始化像素的隸屬度時采取了隨機化的策略,導致所有的聚類中心基本集中在同一強度值,因而無法對圖像的分割進行有效地指導,從而產生圖1(b)中無法分割出圖像的主要成分的情況;(2)聚類中心的計算與圖像中的所有像素有關,導致算法在迭代過程中效率過慢,而這點明顯不符合醫學圖像的特點。
基于上述分析,本文做出如下假設:一個組織或器官的像素強度值僅取決該器官或組織包含的像素,與其他器官或組織包含的像素無關。基于該假設,本文提出了一種基于分層的FCM算法用于醫學圖像分割。算法主要分為兩個階段,第一階段基于峰值檢測的方法對圖像進行初始化分層,并為相應的分層初始化聚類中心;第二階段最小化基于分層的目標函數,對圖像的分層進行修正,最終完成對圖像的分割。
2.1 基于峰值檢測的圖像分層
根據本文的假設,聚類中心將取決于該像素所在的組織或器官,因此需要修訂經典FCM算法中像素隸屬度的隨機初始化方案。為此,本文將基于峰值檢測技術[19]對圖像進行初始化分層。假設預設的聚類數目為C,圖像的直方圖為H,初始化分層的算法描述如下。
Step 1 求取H上的所有極大值點組成的集合P,即,P={i|H(i)>H(i+1)且H(i)>H(i-1)};
Step 2 如果card(P)≤C,令C=card(P),轉Step 5;否則,轉下一步;

Step 4 刪除關聯像素數最少的極值點,并將它關聯的像素與鄰近的兩個極值點重新關聯后,轉Step 2;
Step 5 根據圖像關聯的極值點對圖形進行分層。
對圖1(a)的直方圖進行峰值檢測,假設C=4,通過上述算法獲得的四個峰值為10、58、67和82,如圖2所示。根據像素關聯的峰值,對圖像進行分層。
2.2 基于分層的改進FCM算法
本部分將對基于分層的FCM算法進行詳細介紹。假設圖像在初始化過程中形成的分層為A1,A2,…,AC,本文算法將通過最小化如下的目標函數對圖像進行分割:
(12)
其中vi是Ai層次的聚類中心,定義為
(13)
同時,在最小化(12)式中目標函數的過程中,根據像素的隸屬度對圖像的分層不斷進行修正, 具體如下:
(14)
通過最小化(12)中的目標函數,對初始化分層進行修正,最終對圖像完成分割。算法的形式化描述如下:
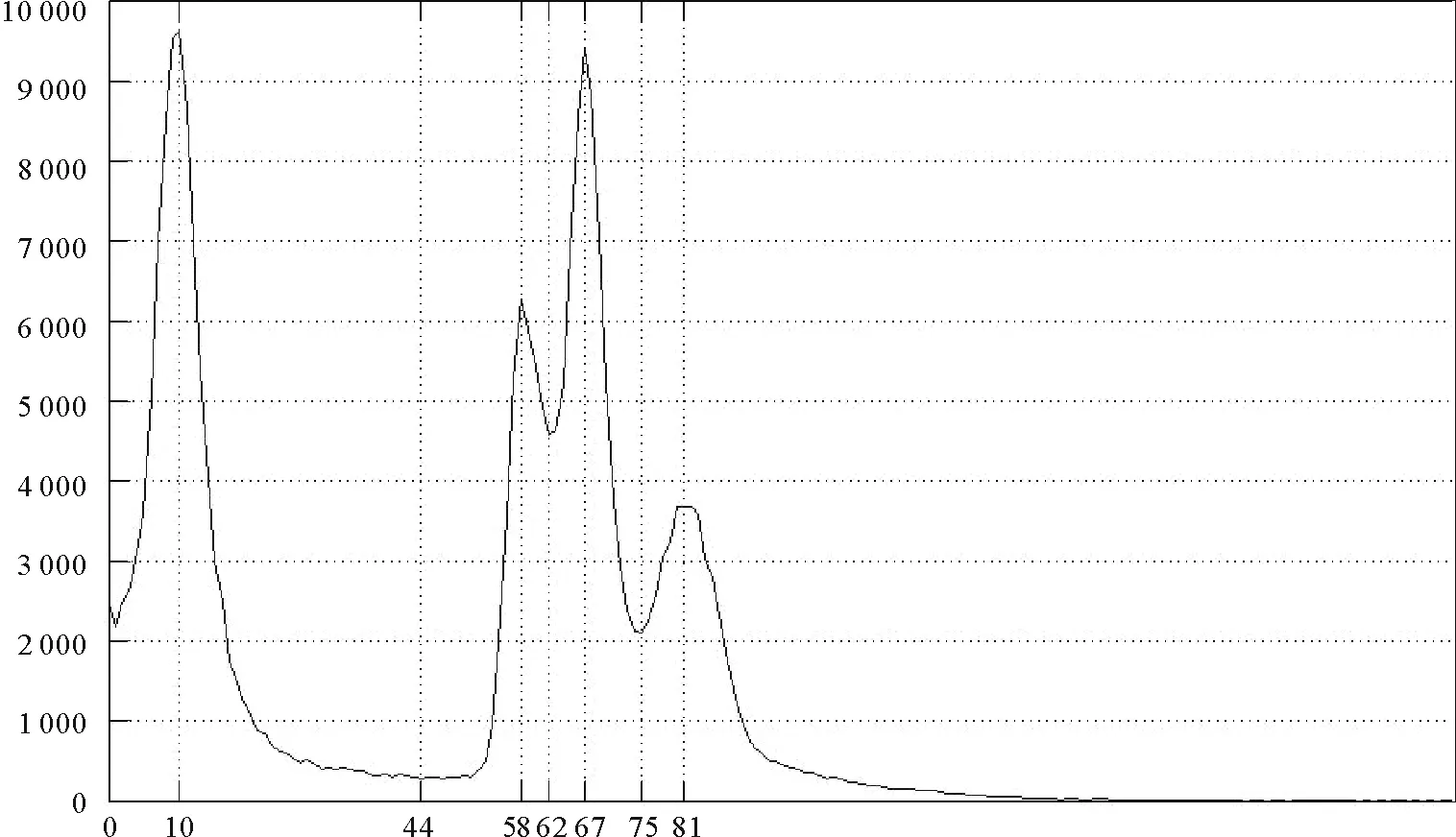
圖2 圖1(a)的灰度直方圖
Step 1 根據(13)式計算每一分層的聚類中心;
Step 2 根據(3)式初始化隸屬度μij;
Step 3 根據(12)式計算目標函數F;
Step 4 根據(14)式對圖像的分層進行修正;
Step 5 根據(13)式和(3)式更新聚類中心以及隸屬度,計算新的目標函數F′;
Step 6 如果|F-F′| Step 7 根據像素的分層完成對原圖像的分割。 本部分將首先以圖3所示的幾幅醫學CT圖像為例詳細說明本文提出算法的執行過程,并將其與FCM、FCMS、EnFCM等算法進行比較。需要說明的是,實驗所選取的四幅醫學圖像均為真實的灰度圖像,其中breast、head和tumor三幅圖像的尺寸均為512×512,圖像brain的尺寸為200×217。 3.1 分割后圖像的視覺效果比較 實驗過程首先從視覺效果上對FCM、FCMS、EnFCM和本文提出的算法進行分割后的圖像進行比較。實驗中相關參數具體設置為:C=4,threshold=0.000 01,m=2,α=2.0,實驗過程允許算法迭代的最大次數為100次,具體分割結果如圖4所示。這里需要說明的是,threshold的取值是經驗取值,m的取值是參照相關的算法[9-12]取值,如果圖像中沒有明確的說明,根據四色定理,可以用4種不同的顏色對不同的區域標記,因而預置的分類數C通常設為4。 圖3 實驗中選用的醫學CT圖像 從分割后的視覺效果看,FCM和FCMS算法過于集中在圖像的細小部分,而忽略了圖像的主要區別,如breast圖像的分割結果。同時,由于FCMS算法在分割過程中考慮了像素的鄰域信息,因此分割結果中出現的“碎小”區域較少。本文算法有效結合FCM和EnFCM算法的優點,既考慮了圖像的細節部分分割較為清楚,同時又考慮了圖像的主要部分,這在breast圖像中尤為明顯。從視覺效果上綜合考慮,FCMS和本文算法的分割效果最好,FCM算法次之,而EnFCM算法的分割效果較差。 圖4 相關算法的分割結果 3.2 分割后圖像的聚類質量比較 對聚類分析后圖像的質量比較,有各種各樣的評價標準,本文從中選擇了3個評價標準。 3.2.1 Bezdek劃分系數 第一個量化評價標準稱為Bezdek劃分系數[20],定義如下: (14) 從VPC的定義來看,一個好的聚類應使圖像中像素屬于某一類的隸屬度盡可能大,而屬于其他類的隸屬度盡可能小。因此,一個好的聚類算法的VPC值應盡可能地大。實驗對4種算法的Bezdek劃分系數進行了計算,結果見表1,其中黑體代表最優值。 從表1中可以看出,從Bezdek劃分系數進行比較時,本文算法在這四種算法中最好,FCM次之,FCMS和EnFCM較差,這也與本文算法假設像素強度值僅取決于它所在的組織包含的像素強度值是一致的。 3.2.2 Liu系數 Liu在進行多分辨率彩色圖像分割時,提出了一種Liu系數[21],用以描述分割后圖像與原圖像的差別,本文對其中的距離進行了修正,使其可以運用在灰度圖像的分割效果評價上,定義如下: 表1 Bezdek劃分系數VPC的比較Table 1 The comparison of Bezdek parameter VPC (16) 表2 圖像分割后F(I)的比較 從表2中可以看出,從與原圖像的比較來看,4個算法中,FCM和本文算法較好,FCMS算法次之,EnFCM算法表現較差。對于FCMS算法,由于它在處理圖像時考慮了像素的鄰域信息,因此,其F(I)值比FCM算法稍大可以理解。 3.2.3 重構錯誤率 重構錯誤率(Reconstruct error)是由Pedrycz提出的[22-23],指的是利用分割后的圖像對原圖像進行重構后,與原圖像之間的差別,具體定義如下: (18) (19) 從(18)式重構錯誤率的定義可以看出,對分割后的圖像進行重構后,當然希望所得到的圖像與原圖像盡可能地相似,因此,一個好的圖像分割算法應具有較小的重構錯誤率。實驗過程對4種算法分割后的圖像進行了重構,結果如圖5所示。 圖5 利用分割結果重構的圖像 從圖5中重構后的視覺效果看,FCM、FCMS和本文提出的算法重構的圖像包含的區域同質性強,效果要好于EnFCM。同時,實驗過程對各算法的重構錯誤率進行了計算,結果見表3。 從表3可以看出,本文算法的重構錯誤率要略好于FCM算法和FCMS算法的重構錯誤率,明顯好于EnFCM算法,這說明利用本文算法重構的圖像更接近原圖像。 表3 4種算法的重構錯誤率比較Table 3 The comparison of reconstruction error rate for four algorithms 3.3 運行時間比較 一個好的聚類算法不僅要有好的視覺效果、好的質量,也必須具備好的運行效率,否則無法滿足圖像處理的要求。為此,實驗對FCM、FCMS、EnFCM和HisFCM這4種算法的運行時間進行了比較,算法均運行在相同的計算機軟硬件環境,編程采用MATLAB R2010b實現,具體運行時間如表4所示。 表4 4種算法的運行時間比較(單位:s)Table 4 The comparison of run time cost for four algorithms 從表4可以看出,EnFCM算法由于利用了圖像的統計信息,因此的運行時間最短,而本文算法的運行效率相比FCM算法提高了一倍左右,遠高于FCMS的運行效率。 可以看出,本文提出的算法可以取得與目前的FCM系列算法相媲美的分割結果,且其運行效率也較FCM和FCMS算法提高了一倍以上。從視覺效果、圖像的分割質量以及算法的運行時間3個方面綜合考慮,本文提出的算法要優于當前FCM的相關改進算法。 本文基于峰值檢測技術,提出了一種基于分層的改進模糊聚類算法。算法將FCM算法、FCMS算法和EnFCM算法的優點進行了有機的結合,既保證了較好的分割效果,又具有較高的運行效率,可以滿足醫學圖像處理的要求。 [1] Jerry L Prince Dzung L Pham, Chengyang Xu. A survey of concurrent methods in medical image segmentation[J]. Annual Review of Biomedical Engineering, 2000, 2: 315-337. [2] Ze-Xuan Ji, Quan-Sen Sun, De-Shen Xia. A framework with modified fast FCM for brain MR images segmentation[J]. Pattern Recognition, 2011, 44: 999-1013. [3] Ji Z X, Sun Q S, Xia D S. A modified possibilistic fuzzy c-means clustering algorithm for bias field estimation and segmentation of brain MR image[J]. Comput Med Imaging Graph, 2011, 35(5): 383-397. [4] Wang Y, Zhou H. Total Variation Wavelet-Based Medical Image Denoising[J]. International Journal of Biomedical Imaging, 2006, 2006(3): 89095. [5] K Van Leemput, F Maes, D Vandermeulen, et al. Automated model- based tissue classification of MR images of the brain[J]. IEEE Transactions on Medical Imaging, 1999, 18(10): 897-908. [6] FU ShuJun, Zhang Caiming. Adaptive bidirectional diffusion for image restoration[J]. Sci China Inf Sci, 2010, 53(12): 2452-2460. [7] Iyer N S, Kandel A, Schneider M. Feature-based fuzzy classification for interpretation of mammograms[J]. Fuzzy Sets & Systems, 2000, 114(2): 271-280. [8] Alsmadi M K. A hybrid firefly algorithm with fuzzy-c mean algorithm for MRI brain segmentation[J]. American Journal of Applied Sciences, 2014, 11(9): 1676-1691. [9] Bezdek J C, Hall L O, Clarke L P. Review of MR image segmentation techniques using pattern recognition[J]. Medical Physics, 1993, 20(4): 1033. [10] Ahmed M N, Yamany S M, Mohamed N, et al. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3): 193-9. [11] Cai W, Chen S, Zhang D. Fast and robust fuzzy c -means clustering algorithms incorporating local information for image segmentation[J]. Pattern Recognition, 2007, 40(3): 825-838. [12] Szilagyi L, Benyo Z, Szilagyi S M, et al. MR brain image segmentation using an enhanced fuzzy C-means algorithm[C]. International Conference of the IEEE Engineering in Medicine and Biology Society, 2003(1): 724-726. [13] Sharon Chen, Jay Wu, Tzong-Jer, et al. Fuzzy c-means clustering with spatial information for image segmentation[J]. Computerized Medical Imaging and Graphics, 2006, 30: 9-15. [14] Xiang-Yang Wang, Juan Bu. A fast and robust image segmentation using fcm with spatial information[J]. Digital Signal Processing, 2010, 20: 1173-1182. [15] Graves D, Pedrycz W. Kernel-based fuzzy clustering and fuzzy clustering: A comparative experimental study[J]. Fuzzy Sets & Systems, 2010, 161(4): 522-543. [16] Zhang Y, Huang D, Ji M, et al. Image segmentation using PSO and PCM with Mahalanobis distance[J]. Expert Systems with Applications, 2011, 38(7): 9036-9040. [17] Kannan S R, Ramathilagam S, Devi R, et al. Robust kernel FCM in segmentation of breast medical images[J]. Expert Systems with Applications, 2011, 38(4): 4382-4389. [18] Caldairou B, Passat N, Habas P A, et al. A non-local fuzzy segmentation method: Application to brain MRI[J]. Pattern Recognition, 2011, 44(9): 1916-1927. [19] Khang Siang Tan, Nor Ashidi Mat Isa. Color image segmentation using histogram thresholding-Fuzzy C-means hybrid approach[J]. Pattern Recognition, 2011, 44: 1-15. [20] James C Bezdek. Cluster Validity with Fuzzy Sets[J]. Journal of Cybernetics, 1973, 3(3): 58-73. [21] Liu J, Yang Y H. Multiresolution Color Image Segmentation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1994, 16(7): 689-700. [22] Cheng J, Cline M, Martin J, et al. A knowledge-based clustering algorithm driven by Gene Ontology[J]. Journal of Biopharmaceutical Statistics, 2004, 14(3): 687. [23] Graves D, Pedrycz W. Kernel-based fuzzy clustering and fuzzy clustering: A comparative experimental study[J]. Fuzzy Sets & Systems, 2010, 161(4): 522-543. Abstract: Image segmentation is focused and difficult in the aspect of medical image processing, and the phenomena of the partial volume effect and the intensity inhomogeneity makes the segmentation more difficult. Though the method of FCM can solve the problem of partial volume effect, the computational cost is very big. A method of medical segmentation based on layered FCM has been proposed in this paper. The premise of this method is assumed that the cluster centroids are produced from the same or similar organ or tissue, rather than from others. Then the segmentation intensity inhomogeneity can be solved, moreover the run time of the proposed method is decreased dramatically. The experimental results on different medical images verify the efficiency and effectiveness of the proposed method. Key words: Layered FCM; image segmentation; medical image processing 責任編輯 陳呈超 Medical Image Segmentation Based on Layered FCM SUN Yu-Juan, WANG Zeng-Feng, ZHANG Xiao-Feng (School of Information and Electrical Engineering, Ludong University, Yantai 264025, China) TP391 A 1672-5174(2017)11-124-08 10.16441/j.cnki.hdxb.20160425 孫玉娟, 王增鋒, 張小峰. 基于分層的FCM算法在醫學圖像分割中的應用[J]. 中國海洋大學學報(自然科學版), 2017, 47(11): 124-131. SUN Yu-Juan, WANG Zeng-Feng, ZHANG Xiao-Feng. Medical image segmentation based on layered FCM[J]. Periodical of Ocean University of China, 2017, 47(11): 124-131. 國家自然科學基金項目(61602229);山東省自然科學基金項目(ZR2016FM13;ZR2016FM21)資助 Supported by NSFC Under Granted(61602229);NSFC of Shandong Province Under Granted(ZR2016FM13;ZR2016FM21) 2016-06-15; 2016-11-12 孫玉娟(1977-),女,博士。E-mail: syj_anne@163.com3 實驗






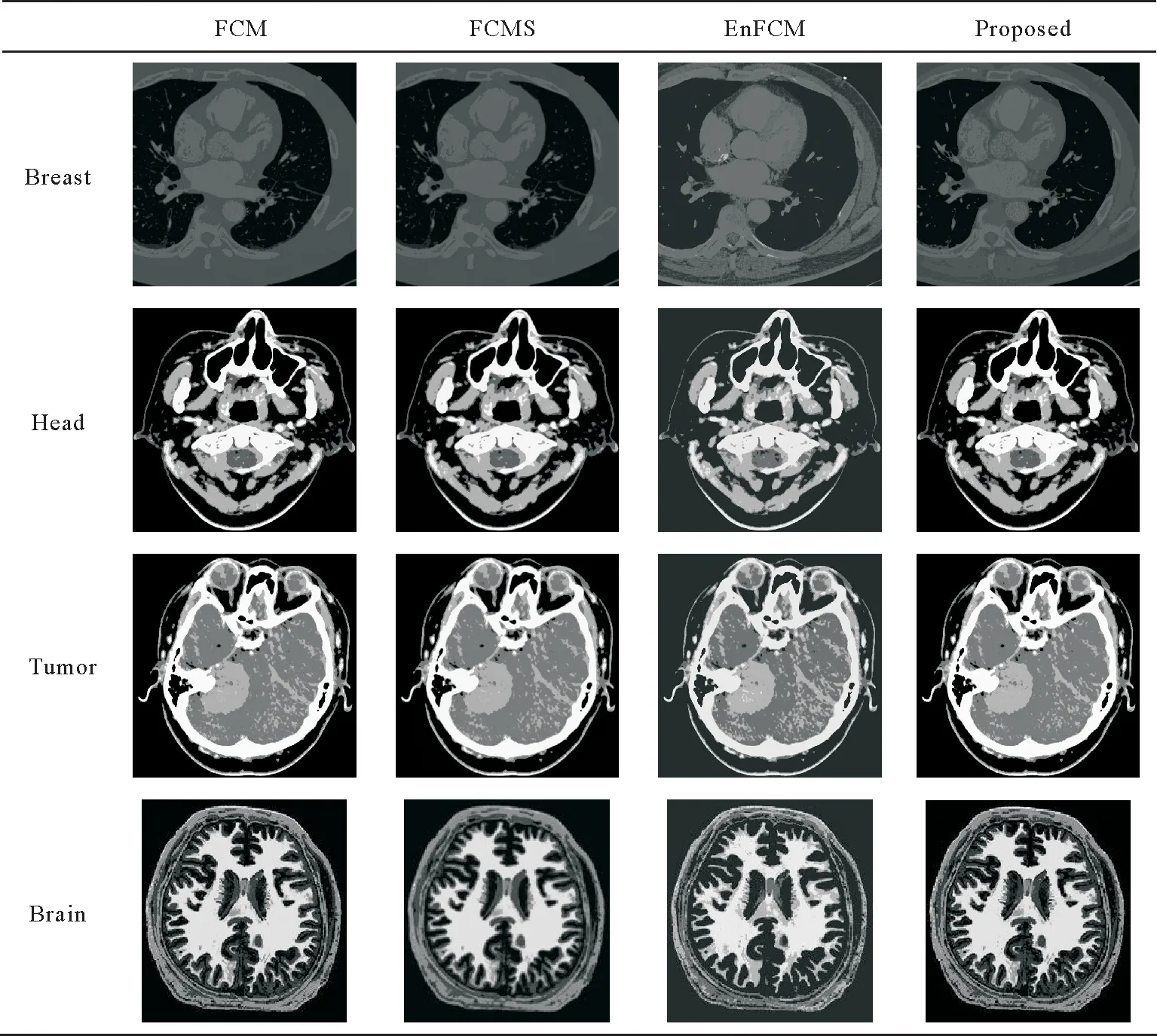
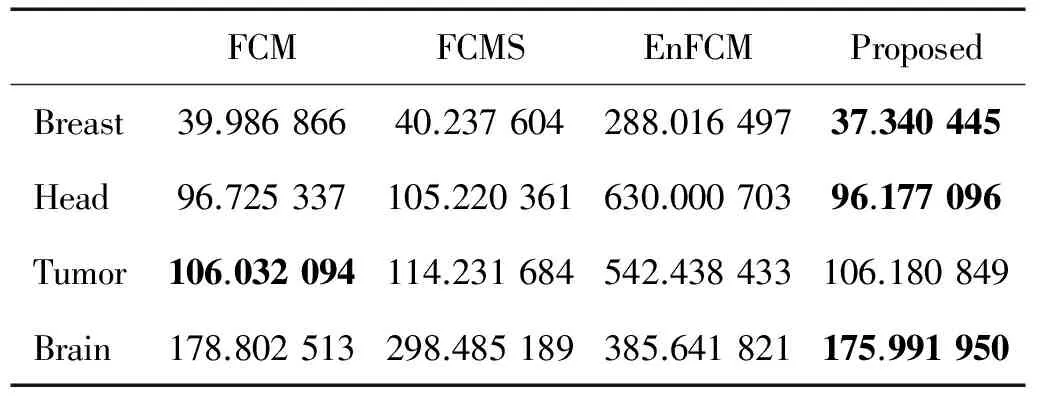

4 結語

