關(guān)于超級(jí)有窮條件下角域內(nèi)的亞純函數(shù)的唯一性*
李效敏, 劉 翠, 徐會(huì)彩, 孫文江
(1.中國(guó)海洋大學(xué)數(shù)學(xué)科學(xué)學(xué)院, 山東 青島 266100; 2.中國(guó)人民大學(xué)信息學(xué)院, 北京 100872)
關(guān)于超級(jí)有窮條件下角域內(nèi)的亞純函數(shù)的唯一性*
李效敏1, 劉 翠1, 徐會(huì)彩2, 孫文江1
(1.中國(guó)海洋大學(xué)數(shù)學(xué)科學(xué)學(xué)院, 山東 青島 266100; 2.中國(guó)人民大學(xué)信息學(xué)院, 北京 100872)
研究了復(fù)平面上的亞純函數(shù)在超級(jí)有窮條件下在角域內(nèi)分擔(dān)2個(gè)有限集合的唯一性問(wèn)題,改進(jìn)和推廣了儀洪勛和林偉川,以及吳召君等人的有關(guān)結(jié)果。
角域Nevanlinna theory;亞純函數(shù);分擔(dān)值; 唯一性定理
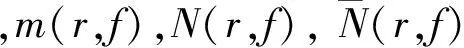
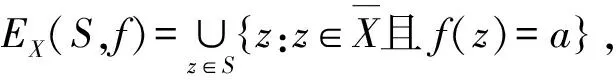
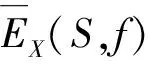
另外, 本文需要下述2個(gè)定義:
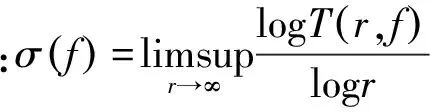
1958年,熊慶來(lái)證明了下述結(jié)果:
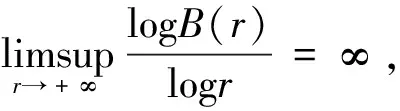
(1)ρ(r)是區(qū)間[r0,+∞)上的連續(xù)非減函數(shù),其中r0>0是1個(gè)正數(shù),并且當(dāng)r→+∞時(shí),有ρ(r)→+∞。
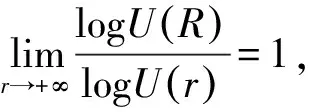
由定理A本文給出以下定義:
定義1.2[4-5]假設(shè)g是無(wú)窮級(jí)亞純函數(shù), 并且T(r,g)=B(r), 其中B(r)由定理A定義,若存在連續(xù)可微函數(shù)ρ(r)滿足定理A的條件,則稱ρ(r)和U(r)分別是B(r)的階函數(shù)和型函數(shù),并稱ρ(r)為亞純函數(shù)g的無(wú)窮級(jí)。
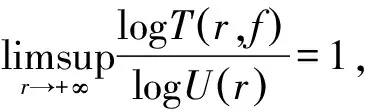

1929年,Nevanlinna[6]證明了著名的五值定理和四值定理。后來(lái), Gundesen[7-9]和 Mues[10]對(duì)具有四個(gè)公共值的亞純函數(shù)的唯一性問(wèn)題做了一些進(jìn)一步的研究工作。2004年,鄭建華[11-12]開(kāi)始了角域內(nèi)的亞純函數(shù)唯一性問(wèn)題的研究。2006年,Lin- Mori-Tohge[13]在超級(jí)有窮的條件下,研究了在1個(gè)角域內(nèi)具有2個(gè)公共值的和3個(gè)公共值的亞純函數(shù)的唯一性問(wèn)題,改進(jìn)Gross[14]和Yi[15]中的相應(yīng)結(jié)果。最近吳昭君[16]改進(jìn)了文獻(xiàn)Lin- Mori-Tohge[13]中的相應(yīng)結(jié)果。本文將進(jìn)一步研究超級(jí)有窮條件下亞純函數(shù)在角域內(nèi)分擔(dān)兩個(gè)有限集合的唯一性問(wèn)題。
1977年,Gross[14]提出了下述問(wèn)題:
問(wèn)題 A[14]能否找到兩個(gè)有限集合S1與S2,使得對(duì)任意2個(gè)非常數(shù)的整函數(shù)f與g,只要滿足E(S1,f)=E(S1,g)和E(S2,f)=E(S2,g), 就有f=g。
1995,儀洪勛肯地回答了問(wèn)題A, 證明了下述定理:
定理 B[16-17]設(shè)S={ω:ωn+aωn-1+b=0},其中n≥7是一個(gè)正整數(shù),a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。如果非常數(shù)的整函數(shù)f與g滿足E(S,f)=E(g,S),那么f=g。
后來(lái),Lahiri[18]和Fang-Lahiri[19]推廣了定理B, 分別證明了下述結(jié)果:
定理 C[18]假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合,其中a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。如果n≥8,并且對(duì)2個(gè)沒(méi)有單極點(diǎn)的非常數(shù)的亞純函數(shù)f與g滿足E(S1,f)=E(S1,g)和E(S2,f)=E(S2,g),那么f=g。
定理 D[19]假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合,其中a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。如果n≥7,并且對(duì)2個(gè)沒(méi)有單極點(diǎn)的非常數(shù)的亞純函數(shù)f與g滿足E(S1,f)=E(S1,g)和E(S2,f)=E(S2,g),那么f=g。
2006年,Yi-Lin[20]證明了下述結(jié)果, 改進(jìn)了定理 C:
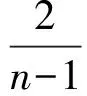
針對(duì)定理 E, 人們自然要問(wèn):
問(wèn)題B[21,問(wèn)題 1 ]是否存在某個(gè)角域X=X(α,β)={z:α≤argz≤β},其中α,β是2個(gè)實(shí)數(shù)且滿足0<β-α<2π, 使得對(duì)任意2個(gè)非常數(shù)的整函數(shù)f與g,只要滿足EX(S1,f)=EX(S1,g)和EX(S2,f)=EX(S2,g), 就有f=g?
吳昭君[21]回答了問(wèn)題1, 證明了下述定理:
定理 F[21,定理 1 ]假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合, 其中a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。記
X=Xθ,ε:={z:θ-ε 針對(duì)定理 F, 人們自然要問(wèn):將定理F的條件“f,g∈M(ρ(r))”換為“f∈M(ρ(r))”, 定理F的結(jié)論是否成立? 本文在超級(jí)有窮條件下研究了該問(wèn)題,證明了下述定理: 定理 1.1 假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合,其中a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。記 X=Xθ,ε:={z:θ-ε 如果n≥8,并且對(duì)2個(gè)非常數(shù)的亞純函數(shù)f與g滿足 f∈M(ρ(r))且σ2(g)<∞,那么f=g。 由定理1.1可得下述結(jié)果: 推論 1.1 假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合,其中a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。記 X=Xθ,ε:={z:θ-ε 如果n≥8,并且對(duì)2個(gè)非常數(shù)的亞純函數(shù)f與g滿足 如果σ(f)=σ(f)=∞,σ2(f)<∞并且σ2(g)<∞, 那么f=g。 定義 Aα,β(r,f)= (1) (2) 和 (3) Sα,β(r,f)=Aα,β(r,f)+Bα,β(r,f)+Cα,β(r,f)。 為了便于敘述, 接下來(lái)省略上述全部符號(hào)的下標(biāo),對(duì)于每一個(gè)有限值a分別用A(r,a),B(r,a),C(r,a),S(r,a)來(lái)代替Aα,β(r,fa),Bα,β(r,fa),Cα,β(r,fa)和Sα,β(r,fa)。 引理 2.3[13,Lemma 5]假設(shè)F與G是2個(gè)非常數(shù)的亞純函數(shù),并且在X(α,β)上CM分擔(dān)1和∞,那么下述3種情形之一成立: (ii)FG=1 ; (iii)F=G。 引理 2.5[24, Lemma 1.3]假設(shè)f是復(fù)平面上非常數(shù)的亞純函數(shù), 并且f(0)≠0,∞。那么 引理 2.6[22, Lemma3.1]假設(shè)f是復(fù)平面上非常數(shù)的亞純函數(shù), 并且f(0)=1。那么 (4) 引理 2.7 假設(shè)f與g是復(fù)平面上無(wú)窮級(jí)亞純函數(shù), 并且f(0)=1和σ2(g)<∞。如果f∈M(ρ(r)),U(r)=rρ(r),那Q(r,f)+Q(r,g)=O{logU(r)+rσ2(g)+ε0}。 證明 設(shè) (5) 由(2.2),(2.5),定理 A 和引理2.5可得 4log+r+10+4log2), 即 4log+r+10+4log2)。 (6) 由引理2.6可得(4)。將(5)代入(4),再由定理A可得 K(4·2ωlogU(r)+loglog(1+logU(r))+1+log2), 即 K(4·2ωlogU(r)+loglog(1+logU(r))+1+log2)。 (7) 由(6),(7)和引理 2.2可得 Q(r,f)=O(logU(r)), (8) 同理 Q(r,g)=O(logU1(r)), (9) 其中U1(r)=rρ1(r),ρ1(r)為g的無(wú)窮級(jí)。由σ2(g)<∞和定理 A可得 logU1(r)=O(rσ2(g)+ε0), (10) 其中ε0>0為常數(shù)。由(8)~(10)可得引理2.7的結(jié)論。 引理2.8[22,Lemma6]假設(shè)S1={∞}和S2={ω:ωn+aωn-1+b=0}是2個(gè)集合, 其中n≥8,a與b是使得代數(shù)方程ωn+aωn-1+b=0具有n個(gè)判別的根的非零常數(shù)。記X=Xθ,ε:={z:θ-ε Q(r,f)+Q(r,g)。 引理 2.9[22,Lemma 2]假設(shè) (11) 定理1.1 的證明:首先設(shè)定(11)。 由定理1.1的條件可知,F(xiàn)與G在X上CM分擔(dān)1和∞。 由引理2.3我們分以下3種情形討論: 情形1 假設(shè)引理2.3的結(jié)論(i)成立并且F不恒等于G。由(11),引理2.8和引理2.7可知 Q(r,f)+Q(r,g)+O(logU(r)+rσ2(g)+ε0)≤ (12) 其中 S1(r)=max(S(r,f),S(r,g))。 (13) 再由(11),(12)和引理 2.1可得 S(r)=nS1(r)+O(1), (14) 其中符號(hào)S(r)和引理2.3中出現(xiàn)的S(r)含義相同。 由(12)和(14)可得 (15) 由(15)和引理2.3(i)可知 (16) 由條件`n≥8可知 (17) 由(16),(17)和引理 2.4可得 矛盾。 情形2 假設(shè)引理2.3的結(jié)論(ii)成立并且F不恒等于G。引理2.3的結(jié)論(ii)和(11)可得 [fn-1(f+a)][gn-1(g+a)]=b2。 (18) 注意到f與g是非常數(shù)的亞純函數(shù),并且b≠0,由(18)和條件f與g在角域Xθ,ε內(nèi)分擔(dān)∞可知:0,-a,∞為f在角域Xθ,ε內(nèi)的三個(gè)Picard例外值,這與f∈M(ρ(r)),從而射線J:argz=θ為f的一個(gè)ρ(r)級(jí)Borel方向矛盾。 情形 3 假設(shè)引理2.3的結(jié)論(iii)成立,即F=G。由條件由條件n≥8和引理 2.9可得f=g。于是完成了定理1.1的證明。 [1] Yang C C, Yi H X. Uniqueness Theory of Meromorphic Functions[M]. Dordrecht/Boston/London: Kluwer Academic Publishers,2003. [2] Gross F. On the distribution of values of meromorphic functions[J]. Trans Amer Math Soc, 1968, 131:199-214. [3] Laine I. Nevanlinna Theory and Complex Differential Equations[M].Berlin/New York: Walter de Gruyter, 1993. [4] Chuang C T. On Borel directions of meromorphic functions of infinite order II[J], Bull Hongkong Math Soc, 1999, 2: 305-323. [5] Hiong K L. Sur les fonctions entiéres etles fonctions (in Chinese) [M]. Beijing: Science Press, 1958. [6] Nevanlinna R. Le Théorème de Picard-Borel et la Théorie des Fonctions Méromorphes [M]. Paris:Gauthier-Villars, 1929. [7] Gundersen G G. Meromorphic functions that share three or four values [J]. J London Math Soc, 1979, 20: 457-466. [8] Gundersen G G. Meromorphic functions that share four values[J]. Trans Amer Math Soc, 1983, 227:545-567 (Correction: 1987, 304: 847-850). [9] GundersenG G. Meromorphic functions that share three values IM and a fouth value CM[J]. Complex Variables Theory Appl, 1992, 20: 99-106. [10] Mues E. Meromorphic functions sharing four values[J]. Complex Variables Theory Appl, 1989, 12: 169-179. [11] Zheng J H. On uniqueness of meromorphic functions with shared values in one angular domains[J]. Complex Variables Theory Appl, 2003, 48: 777-785. [12] Zheng J H. On uniqueness of meromorphic functions with shared values in some angular domains[J]. Canad J Math, 2004, 47: 152-160. [13] Lin W C, Mori S, Tohge K. uniqueness theorems in an angular domain[J]. Tohoku Math J, 2006, 58: 509-527. [14] Gross F. Factorization of meromorphic functions and some probloms. Complex analysis[M]. Berlin: Springer, 1976, 599: 51-69. [15] Yi H X. On a question of Gross concerning uniqueness of entire functions[J]. Bull Austral Math Soc, 1998, 57: 343-349. [16] Yi H X. On a question of Gross[J]. Science in China, Ser A,1995, 38(1): 8-16. [17] Yi H X. A question of Gross and the uniqueness of entire functions[J]. Nogaya Math J, 1995, 138: 169-177. [18] Lahiri I. The range set of meromorphic derivatives[J]. Chinese Northeast Math J, 1998, 14(3): 353-360. [19] Fang M L, Lahiri I. Unique range set for certain meromorphic functions[J]. Indian J Math, 2003, 45(2):141-150. [20] Yi H X, Lin W C. Uniqueness of meromorphic functions and a question of Gross[J]. Kyungpook Math J, 2006, 46: 437-444. [21] 吳昭君. 角域內(nèi)亞純函數(shù)的唯一性定理[J]. 數(shù)學(xué)物理學(xué)報(bào). 2010, 30A(3): 793-799. Wu Zhaojun. Uniqueness of meromorphic functions in an angular clmain[J]. Acta Mathematica Scientia. 2010, 30A(3): 793-799. [22] Gol’dberg A A, Ostrovskii I V. Value Distribution of Meromorphic Functions[M]. 2nd Edition (Translations of Mathematical Monographs), American Mathematical Society,Providence, Rhode Island, 2008, 236. [23] Hayman W K. Meromorphic Functions[M].Oxford: Clarendon Press, 2007. [24] Yang L. Value Distribution Theory[M]. Berlin Heidelberg: springr-Verlag, 1993. Abstract: In this paper, we study the uniqueness questions of meromorphic functions sharing two finite sets in an angular domain. The results in this paper improve and extend the corresponding results given by Yi -Li[20]and Wu[21]. Key words: Nevanlinna theory in angular; Meromorphic functions; shared values; uniqueness theorems AMS Subject Classifications: 30D35;30D30 責(zé)任編輯 陳呈超 Uniqueness of Meromorphic Functions of Finite Hyper-Order in an Angular Domain LI Xiao-Min1, LIU Cui1, XU Hui-Cai2, SUN Wen-Jiang1 (1.School of Mathematical Sciences, Ocean University of China,Qingdao 266100, China; 2.School of Informaition, Renmin University of China, Beijing 100872, China) O174.52 A 1672-5174(2017)11-132-05 10.16441/j.cnki.hdxb.20140279 李效敏, 劉翠, 徐會(huì)彩, 等. 關(guān)于超級(jí)有窮條件下角域內(nèi)的亞純函數(shù)的唯一性[J]. 中國(guó)海洋大學(xué)學(xué)報(bào)(自然科學(xué)版), 2017, 47(11): 132-136. LI Xiao-Min, LIU Cui, XU Hui-Cai, et al. Uniqueness of meromorphic functions of finite hyper-order in an angular domain[J]. Periodical of Ocean University of China, 2017, 47(11): 132-136. 國(guó)家自然科學(xué)基金項(xiàng)目(11171184);山東省自然科學(xué)基金項(xiàng)目(ZR2014AM011);中國(guó)人民大學(xué)科學(xué)研究基金項(xiàng)目(16XNH117)資助 Supported by the NSFC(11171184); the NSF of Shandong Province,China(ZR2014AM011);the Research Funds of Renimn University(16XNH117) 2014-09-12; 2015-05-05 李效敏(1967-),男,教授。E-mail: lixiaomin@ouc.edu.cn
1 幾個(gè)引理
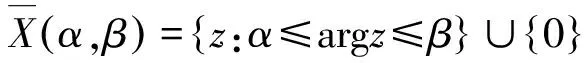


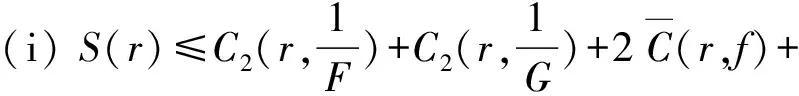
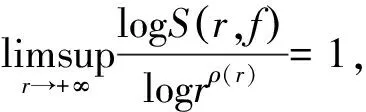
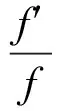
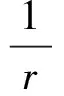
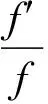
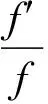
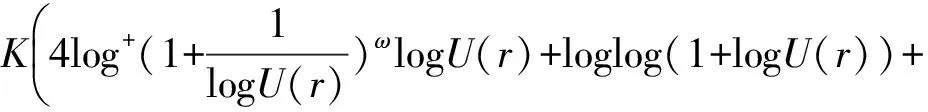
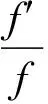
2 定理的證明
 中國(guó)海洋大學(xué)學(xué)報(bào)(自然科學(xué)版)2017年11期
中國(guó)海洋大學(xué)學(xué)報(bào)(自然科學(xué)版)2017年11期
