機械波對脆性材料斷裂的作用

劉建科， 張 誠， 王 騰， 朱婉琳

(1.陜西科技大學 文理學院， 陜西 西安 710021； 2.陜西科技大學 材料科學與工程學院， 陜西 西安 710021)

機械波對脆性材料斷裂的作用

劉建科1， 張 誠1， 王 騰2， 朱婉琳2

(1.陜西科技大學 文理學院， 陜西 西安 710021； 2.陜西科技大學 材料科學與工程學院， 陜西 西安 710021)

在繼承Griffith (格里菲斯)斷裂理論能量觀點的基礎上，通過對產生駐波(機械波形式駐波)現象的脆性材料進行力學理論分析，研究得到了在駐波振動過程中彈性勢能對于脆性材料斷裂的作用.在駐波分析所得結論的基礎之上，將結論推廣應用到一般機械波——行波，研究了加載速率、幾何因素、行波能量大小對脆性材料斷裂的作用，得到了適用于脆性材料斷裂的普適性結論.

駐波； 脆性斷裂； 幾何因素

Abstract:Based on the energy concept of Griffith fracture theory,the impact of elastic potential on brittle materials is gotten by mechanical theory analysis of the brittle materials which producing standing-wave(in this article,the standing-wave is a kind of mechanical wave) phenomenon.On the base of conclusion that the analysis of standing wave phenomenon,the conclusion is spread and applied to universal mechanical wave-traveling wave,the loading rate,geometry factors in the fracture of brittle materials and the energy of traveling wave are researched and the universal conclusion adapting to the fracture of brittle materials are gotten.

Keywords:standing wave; brittle fracture; geometry factory

0 引言

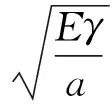
1 產生駐波現象的材料各段受力情況分析

在材料內部，兩列傳輸方向相反、頻率相同的機械波通過相互疊加作用，形成穩定的駐波現象[11].

建立波節處受力模型，圖1為某一時刻的駐波圖形.

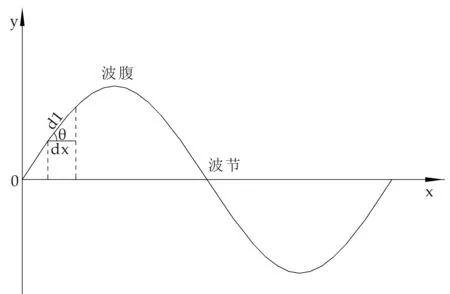
圖1 某時刻駐波波形示意圖

在坐標x處，取dx長度的線元，在其振動過程中線元的長度為dl；θ角為某時刻振動線元切線方向與x軸所在直線的夾角(兩直線夾角取值范圍為0 °～90 °)，在振動過程中線元dx長度的變化量Δ=dl-dx=dl(1-cosθ).在任意時刻，駐波圖形均能由函數式y=Asinx來代替(式中A為一常數，對于確定的駐波而言，時刻確定，則坐標x處線元dx的切線與x軸所在直線的夾角也確定)，對函數式y=Asinx求導得y′=Acosx，當x=kπ(k=0,1,2,3,…)時，|y′|最大，即該點處切線斜率的絕對值最大，即tanθ值最大，θ值最大；x=kπ(k=0,1,2,3,…) 的位置，在駐波波動中即為駐波的波節位置處，因而波節處dx線元的切線與x軸所在直線的夾角在同時刻駐波圖像中最大，因而位于駐波波節處線元dx在振動過程中的形變量Δ最大.

2 彈性勢能在脆性材料斷裂時所起的作用

Griffith從能量觀點來研究裂紋擴展的臨界條件[12].物體內儲存的彈性應變能的降低值大于或等于形成兩個新表面所需的表面能.在求理論強度時曾將此概念用于理想的完整晶體，而Griffith將此概念推廣于有缺陷的裂紋體.Griffith認為物體內儲存的彈性應變能的降低(或釋放)就是裂紋擴展的動力[13].

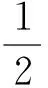
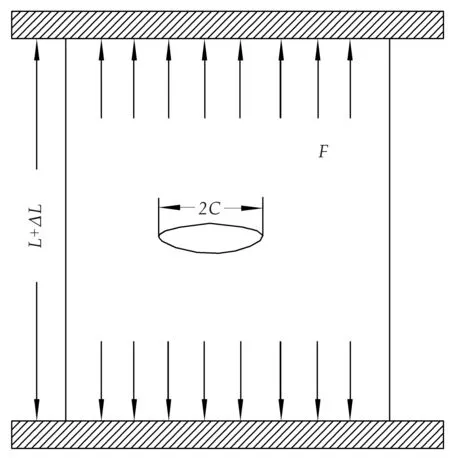
圖2 含有裂紋的板

由此，原來儲存的彈性應變能就要降低，有裂紋后板內儲存的彈性應變能為:

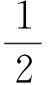
(1)

應變能降低為:

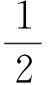
(2)

欲使裂紋進一步擴展，應變能將進一步降低，降低的數量應等于新表面所需的表面能.

由彈性理論可以算出，當人為割開長2C的裂紋時，平面應力狀態下應變能的降低為：

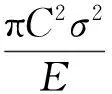
(3)

式(3)中：C為裂紋的半長度，σ為外加應力，E為彈性模量.如為厚板則為平面應變狀態，此時有：

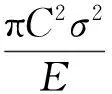
(4)

式(4)中：μ為泊松比.

產生長度為2C，厚度為h的兩個新表面，所需的表面能為:

Ws=4Gγ

(5)

式(5)中：γ為斷裂表面能.

而：

(6)

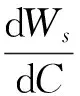
(7)

得到臨界應力：

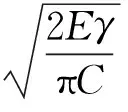
(8)

若為平面應變狀態，則為：

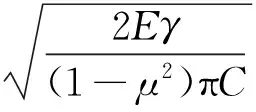
(9)

由(9)式可知，產生駐波現象的脆性材料，假設裂紋尺寸、裂紋密度在概率分布上是均勻的，則斷裂發生最先出現在材料應力最大處，即駐波波節處.在原子間凈約束力接近于其最大值的時候，由于相應的應變量高達0.3～0.4，因而就很難假定Hooke(胡克)定律仍然成立了[14].但對于研究對象為處于臨界斷裂狀態下的波節處線元dx其依然滿足Hooke定律

σ=E′ε

(10)

E′=fE

(11)

式(11)中：f<1為彈性模量修正系數，是與材料相關的確定值.

研究脆性材料產生駐波現象后波節處位置的力學狀態，當受力達到臨界狀態時，有

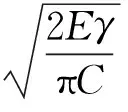
(12)

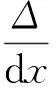
(13)

代(13)入化簡得：

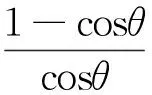
(14)

若為平面應變狀態，則代入化簡得：

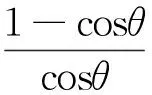
(15)

E、γ、C對于一確定的材料，其均為確定量，式(15)中的θ為駐波波節處線元dl振動達到臨界斷裂狀態時與水平線的夾角，因而θ值也為一確定量.在正弦函數y=Asinnx中，若y=0處各點的斜率y′的絕對值相等，則正弦函數圖像相似，在某時刻的駐波圖像中即波節處線元dl與x軸所在直線的夾角相等，則駐波圖像相似.由之前的討論得知，在脆性材料形成駐波時，達到臨界狀態即將斷裂之時，波節處線元dl與x軸所在直線的夾角為一定值θ，而與形成駐波的其他條件無關.

圖3為相似的正弦函數圖像.在駐波振動過程中，駐波波節處線元dl與x軸所在直線的夾角滿足θ角(脆性材料在振動過程中未斷裂之前的最大θ角，即臨界θ角)相等，即正弦函數圖像相似，脆性材料便在波節處發生脆性斷裂.

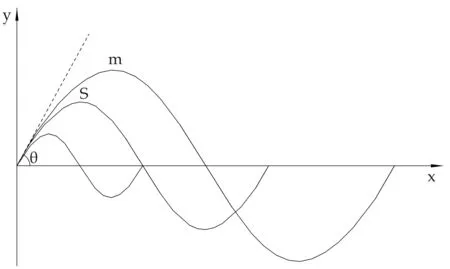
圖3 相似的正弦函數圖像

脆性材料斷裂的本質是能量作用的結果，在注入脆性材料形成駐波的能量之中僅有彈性勢能Ep對脆性材料的斷裂起到直接作用，當脆性材料的形變量大于其斷裂的臨界形變量時，脆性材料發生斷裂.在形成駐波的脆性材料之中，波節處始終處于平衡位置，不做移動，不具有動能，由上推導可知波節處的形變量Δ始終為同時刻駐波圖像各點形變量中的最大值(θ=0 °時除外)，即波節處的線元dx在上述任意時刻都具有同時刻駐波中最大的彈性應變能dEpmax.只有駐波波節處的能量對于脆性材料的斷裂是“有用的”，其他駐波部位的能量對于脆性材料的斷裂是“無用的”. 對于圖3中所示時刻m圖像波節處的線元dx進行能量分析，其彈性勢能為：

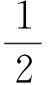
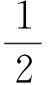
(16)

對于圖3所示時刻s圖像波節處的線元dx進行能量分析，彈性勢能為：

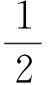
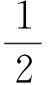
(17)

即有：dEpm=dEps

式(17)中：k為和材料性質有關的常數.

由此可見，如果脆性材料中微裂紋的尺寸大小，裂紋密度分布均勻之時，脆性材料的斷裂強度與脆性材料的幾何尺寸無關，僅僅只取決于駐波波節處線元dx彈性勢能的大小.但在實際工業生產中，由于工藝因素的微弱變動以及環境變化的影響，脆性材料中所存在的微裂紋在尺寸大小、裂紋密度上并不能完全均勻一致，因此對于工業大生產中所得脆性材料其依然具有十分顯著的尺寸效應.

3 行波對脆性材料斷裂的作用

駐波形式的機械波作為機械波中的特例，其在實際材料因振動而發生脆性斷裂的現象之中并不具有普遍性，下面討論實際情況下行波對脆性材料斷裂的作用機理.

在對產生駐波現象的脆性材料，進行各部分的受力分析之中，討論了波節處位置對于脆性材料斷裂的意義；由于波節處線元dx在振動過程中始終處于同時刻駐波中線元形變量Δ值的最大處，因而使得波節處線元dx始終處于“斷裂危險”之中.行波相較于駐波而言，其同樣存在一個類似于駐波中波節處線元dx的“危險位點”，不過與駐波波節處線元dx相對固定的位置不同，行波的“危險位點”隨時間而在材料內部沿著行波傳播方向移動.

圖4為相似的行波圖像.行波u上的e點，在經過π周期后(以行波u的周期為2π)，其沿行波傳播方向移動到i點.將駐波中對于波節處線元dx的力學分析結論應用于對行波“危險位點”的分析，得到脆性材料在行波的作用下，其“危險位點”處的切線與水平t軸所在直線的夾角為θ角時，此時脆性材料中的“危險位點”處于臨界斷裂狀態.

從對駐波現象的分析可知，在分析駐波對脆性材料斷裂的作用時，僅僅考慮了波節處線元dx的作用，而對于形成駐波的其他部位未作適當考慮.

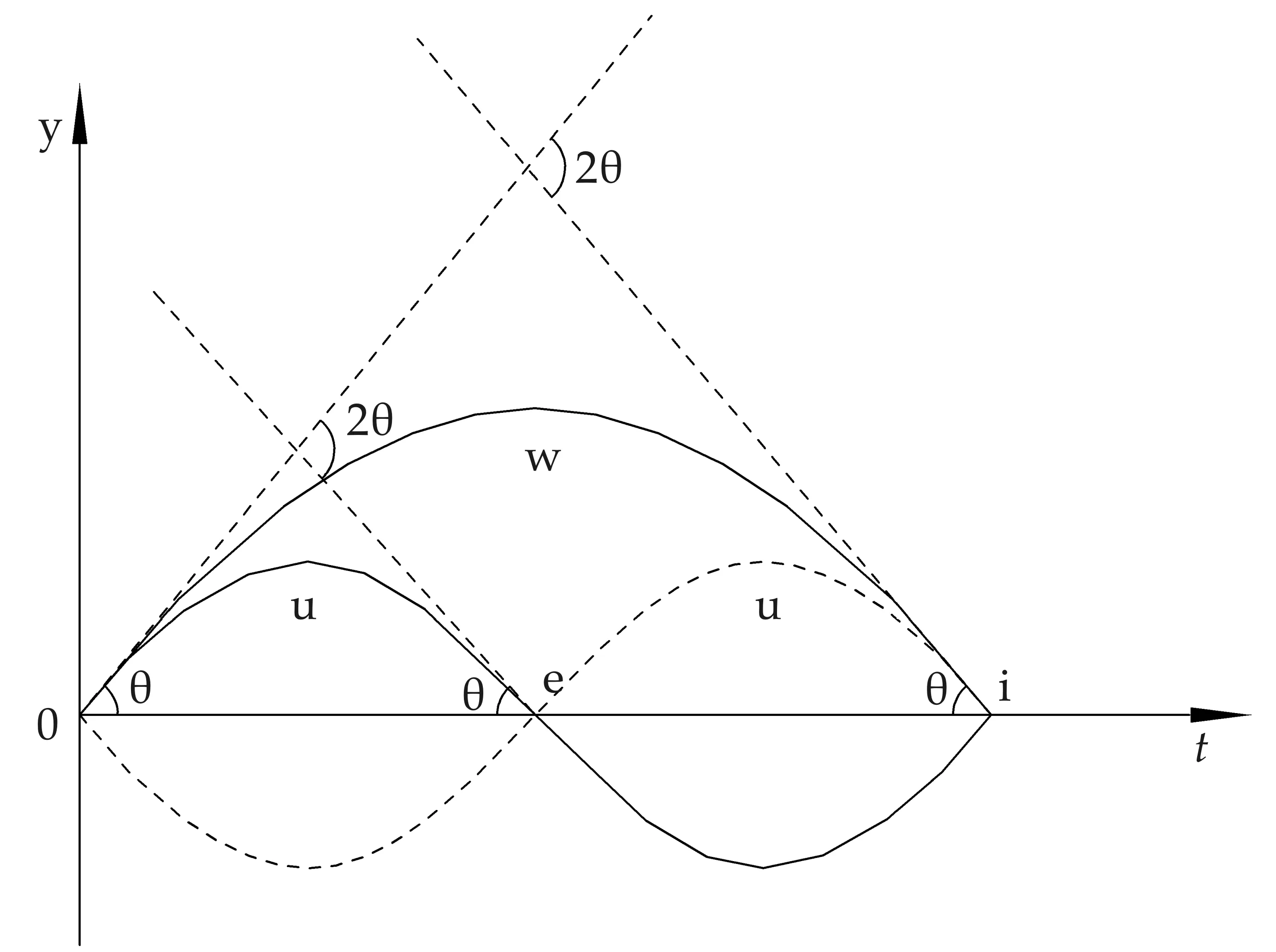
圖4 相似的行波圖像

脆性材料內部產生形波時，脆性材料內部的“結構粒子”會隨著行波而“波動”，在半個行波波長的空間尺度內來看，脆性材料內部“結構粒子”的排列會出現“波谷”和“波峰”的現象，效果相當于在行波半個周期的時間內，外界施加給脆性材料一個“壓頭”，使脆性材料內部的“結構粒子”排列為“波峰”或“波谷”.由此可見在脆性材料中所形成行波的幾何因素對于斷裂的貢獻有著和“壓頭”類似的作用機理.

對于如圖4所示的行波u和w，兩列行波“危險位點”處的線元dx達到同樣臨界形變量Δ值所經歷的時間不同.設行波w的函數表達式為y=Asint，行波u的函數表達式為：

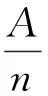
(18)

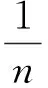
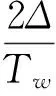
(19)

對于脆性材料而言，加載速率越大，其越容易斷裂.

對于產生行波的脆性材料而言，波動中“結構粒子”所構成波形圖的曲率與脆性材料的斷裂密切相關.對于一確定的脆性材料而言，其彎曲變形程度越大(曲率K越大)，其越容易發生斷裂.

對于一確定的脆性材料，注入脆性材料中的能流密度I越大，脆性材料越容易斷裂.

現假設存在一描述脆性材料斷裂難易程度的物理量ψ.由以上分析討論可知，對于脆性材料在行波波動作用下的斷裂而言，其只需考慮可以代表行波力學狀態、運動行為的半個周期即可.行波半個周期內的弧長l、行波半個周期圖像的平均曲率K、行波半個周期內的能量E、加載速率v與ψ均為正相關性.則有ψ=zlKEv，其中z為比例系數.

根據平均曲率定義可知：

LwKw=2θ與luKu=2θ

(20)

在半個行波周期內注入的能量大小為：

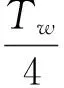
(21)

與：

(22)

聯立代入有：

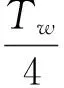
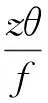
(23)

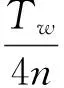
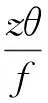
(24)

在產生行波的脆性材料中若滿足ψw=ψu，則兩列行波w，u對于脆性材料的斷裂作用效果是等同的.ψw=ψu從理論上定量的解釋了脆性材料破碎的兩種基本理念——強力低頻破碎和弱力高頻破碎之間的內在聯系.

4 結論

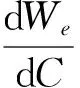
試件的尺寸效應主要是因為其表面及內部的裂紋尺寸大小和裂紋密度的不均勻程度所造成，并隨著試件尺寸的增加而愈加明顯，使試件的強度明顯低于其理論強度.在對產生駐波現象的脆性材料進行力學理論分析的基礎上，將所得結論推廣到更具普遍意義的行波上去，得到了定量描述脆性材料斷裂難易程度的物理量ψ，脆性材料只要滿足ψw=ψu則兩列行波w，u對于脆性材料斷裂的作用效果是等同的.ψw=ψu從理論上定量地解釋了脆性材料破碎的兩種基本理念——強力低頻破碎和弱力高頻破碎的內在聯系.進一步補充了Griffith理論.

[1] Broek D.Elementary engineering fracture mechanics[M].Berlin:Springer Science & Business Media,2012.

[2] Bao Yingbin,Tomasz Wierzbicki.A comparative study on various ductile crack formation criteria[J].Journal of Engineering Materials and Technology,2004,126:314-324.

[3] Orowan E.Fracture and strength of solids[J].Reports on Progress in Physics,1948,12:183-196.

[4] Griffith A A.The phenomena of rupture and flow in solids[J].Philosophical Transactions of the Royal Society of London.Series A,1921,221:163-184.

[5] 李維紅,陳 雄,王懷亮,等.應力比對脆性材料斷裂影響及應變斷裂準則驗證[J].大連理工大學學報,2007,47(3):403-409.

[6] 李維紅,丁 鑄.不同應力比對脆性材料斷裂的影響研究[J].大連大學學報,2007,28(6):88-92.

[7] Hopperstad O S,Borvik T,Langseth M.On the influence of stress triaxiality and strain rate on the behavior of a structural steel:Part I [J].European Journal of Mechanics A：Solids,2003,22:1-13.

[8] Lee S,Ravichandran G.Crack initiation in brittle solids under multiaxial compression [J].Engineering Fracture Mechanics,2003,70:1 645-1 658.

[9] Liu S,Yuh C J,Zhu X K.Tensile-shear transition in mixed-mode I/II fracture [J].International Journal of Solids and Structures,2004,41:6 147-6 172.

[10] 湯安民,師俊平.幾種金屬材料宏觀斷裂形式的試驗研究[J].應用力學學報,2004,21(3):142-144.

[11] 汪曉元,廖 紅,趙 黎,等.大學物理學[M].武漢：武漢理工大學出版社,2008.

[12] 關振鐸,張中太,焦金生.無機材料物理性能[M].北京:清華大學出版社,1992.

[13] 王吉會,鄭俊萍,劉家臣,等,材料力學性能[M].天津:天津大學出版社,2006.

[14] 龔江宏.陶瓷材料斷裂力學[M].北京:清華大學出版社,2001.

【責任編輯：蔣亞儒】

Effectofmechanicalwavesonfractureofbrittlematerials

LIU Jian-ke1， ZHANG Cheng1， WANG Teng2， ZHU Wan-lin2

(1.School of Arts and Sciences, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.School of Materials Science & Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)

2017-08-17

國家自然科學基金項目(51272145，111405100)

劉建科(1966-)，男，陜西西安人，教授，博士，研究方向：材料斷裂力學

2096-398X(2017)05-0189-05

O346.1+1

A