基于三體Lambert算法的平動點交會軌道設(shè)計
孫 俞,張 進(jìn),羅亞中
基于三體Lambert算法的平動點交會軌道設(shè)計
孫 俞1,2,張 進(jìn)1?,羅亞中1
(1.國防科學(xué)技術(shù)大學(xué)航天科學(xué)與工程學(xué)院,長沙410073;2.中國西安衛(wèi)星測控中心宇航動力學(xué)國家重點實驗室,西安710043)
針對未來建設(shè)地月系L2點空間站的需求,提出利用三體Lambert算法研究地月系L2點附近軌道的交會問題,包括設(shè)計同一Halo軌道上不同相位兩航天器之間的交會轉(zhuǎn)移軌道以及設(shè)計不同振幅Halo軌道之間的交會轉(zhuǎn)移軌道。針對現(xiàn)有三體Lambert算法求解長時間軌道轉(zhuǎn)移問題收斂性差的缺陷,提出利用遺傳算法求解初始參考軌道,進(jìn)而通過同倫牛頓-拉夫遜迭代求解目標(biāo)轉(zhuǎn)移軌道的方法。計算結(jié)果表明,該方法能夠有效解決長時間交會軌道轉(zhuǎn)移問題,可以為地月空間平動點區(qū)域空間站建設(shè)提供參考。
三體Lambert算法;軌道交會;地月空間站;Halo軌道;遺傳算法
Abstract:Three-body Lambert algorithm was applied to study the rendezvous problem around the Earth-Moon(EM)L2 libration point aiming at constructing a space station around the EM L2 libration point.The rendezvous transfer trajectory between two spacecraft of different phase on the same Halo orbit and the rendezvous transfer trajectory between two spacecraft on Halo orbits with different amplitudes were designed.Considering the poor convergence of the current three-body Lambert algorithm for solving the long time transfer problems,the transfer trajectory was solved using the approach that the initial reference trajectory was computed by genetic algorithm while the accurate solution was obtained by the homotopy iteration based on the Newton-Raphson algorithm.The results showed that this method could effectively solve the long time three-body rendezvous transfer problem,which could offer a valuable reference for the construction of space station around the cislunar libration point.
Key words:three-body Lambert algorithm; orbital rendezvous; Earth-Moon space station; Halo orbit;generic algorithm
1 引言
21世紀(jì)以來,世界航天技術(shù)快速發(fā)展,各航天大國相繼提出了圍繞月球、近地行星以及小行星的探測計劃。中國也通過“嫦娥”探月工程邁出了深空探測的第一步,并在近地交會對接技術(shù)與空間站建設(shè)方面初步取得了成功。平動點軌道設(shè)計問題在深空探測中具有重要應(yīng)用價值。平動點不僅是對太陽活動進(jìn)行科學(xué)探測的最佳位置,也是進(jìn)行行星際探測的極佳樞紐[1]。地月L2平動點位于地月連線的外側(cè),早在1966年,F(xiàn)arquhar就提出了利用L2點附近的Halo軌道解決地球與月球背面的通信問題[2]。利用地月L2點與日地L1、L2點能級相近的特性,只需很小的能耗就可實現(xiàn)從地月L2點向距地球150萬千米外的日地L1、L2點軌道區(qū)域轉(zhuǎn)移[3]。鑒于地月L2平動點的重要性,未來在其附近建立空間站,將具有為深空探測航天器提供燃料加注、故障檢修、導(dǎo)航通信等服務(wù)的能力。
Koon利用平面Lyapunov軌道的不變流形,設(shè)計了從近地圓軌道到月球的轉(zhuǎn)移軌道[4]。Parker利用Lissajous軌道和Halo軌道的不變流形,設(shè)計了從近地圓軌道到月球的三維轉(zhuǎn)移軌道[5]。針對基于流形設(shè)計節(jié)能轉(zhuǎn)移軌道問題,李明濤提出利用最小二乘策略改進(jìn)傳統(tǒng)的微分修正法,在不降低系統(tǒng)自由度的前提下,得到了微分修正方程的解[6-7];張景瑞等[8]采用遺傳算法與微分修正算法相結(jié)合的混合優(yōu)化策略,設(shè)計了考慮多約束的燃料最優(yōu)地月轉(zhuǎn)移軌道。
空間站的建設(shè)離不開平動點區(qū)域航天器交會對接技術(shù)的支撐[9]。平動點軌道交會對接是交會對接技術(shù)在三體平動點區(qū)域的應(yīng)用,但與二體軌道相比,平動點軌道交會的難度與復(fù)雜性大為增加。三體Lambert問題不存在解析解,需要采用數(shù)值方法迭代求解。在三體Hill模型下,Sukhanov與Prado基于參考軌道,提出了同時修正初、末位置矢量的兩層迭代解法[10],克服了初值選取問題,該方法雖然有較好的收斂性,但是由于三體Lambert問題存在多解,所以不一定能收斂到期望的軌道。平動點軌道的轉(zhuǎn)移,也包括它們之間的轉(zhuǎn)移,Hiday通過選取與兩個Halo軌道都連接的Lissajous軌道,設(shè)計了不同Halo軌道之間的轉(zhuǎn)移軌道,并提出了ERTBP模型下的最優(yōu)交會主矢量理論,然后拓展了無時間約束的非最優(yōu)主矢量理論,并用于優(yōu)化Halo軌道間的轉(zhuǎn)移[11]。Davis通過拼接不同Halo軌道的不穩(wěn)定流形和穩(wěn)定流形,設(shè)計了Halo軌道之間的轉(zhuǎn)移軌道,并利用非最優(yōu)主矢量理論進(jìn)行優(yōu)化[12]。已有研究主要集中在設(shè)計不同Halo軌道之間的轉(zhuǎn)移軌道,并且沒有考慮交會問題中非常重要的時間約束。
本文利用三體Lambert算法,研究同一Halo軌道上不同相位兩航天器交會對接所需速度增量與轉(zhuǎn)移時間的關(guān)系,以及不同幅值Halo軌道之間的交會問題。針對已有三體Lambert算法求解長時間轉(zhuǎn)移軌道收斂性差的問題,提出利用遺傳算法求解參考軌道的方法。
2 圓型限制性三體模型
2.1 動力學(xué)方程
本文選取的動力學(xué)模型為圓型限制性三體模型(CRTBP)。在CRTBP中,兩個主天體繞公共質(zhì)心作圓周運動,而航天器的質(zhì)量遠(yuǎn)小于主天體的質(zhì)量,其對主天體的影響可以忽略不計。本文研究的地月系模型中,主天體的位置分別位于地球質(zhì)心和月球質(zhì)心[13]。
在圓型限制性三體問題中,常用的坐標(biāo)系是質(zhì)心旋轉(zhuǎn)坐標(biāo)系。原點O位于兩個主天體的質(zhì)心,x軸由大天體指向小天體,z軸指向系統(tǒng)的角動量方向,y軸與x軸和z軸構(gòu)成右手坐標(biāo)系。為了使計算方便,對以下物理量做歸一化處理,包括地月距離、地月質(zhì)量之和、萬有引力常數(shù)。地球質(zhì)量為M1,月球質(zhì)量為M2。質(zhì)量常數(shù)μ定義為月球質(zhì)量比地月質(zhì)量之和,如式(1):

歸一化條件下,月球和地球的質(zhì)量分別為μ和1-μ。航天器在質(zhì)心旋轉(zhuǎn)坐標(biāo)系下的運動方程為式(2) ~ (3)[14]:

其中,R1、R2分別為航天器與地球、月球的距離,R1= [(x+μ)2+y2+z2]0.5,R2= [(x-1+μ)2+y2+z2]0.5。
2.2 Halo軌道與狀態(tài)轉(zhuǎn)移矩陣
在平動點周圍存在很多周期軌道,最為常用的是Halo軌道。利用Richardson給出的Halo軌道三階近似解析解[15],可以得到計算Halo軌道的初值,再通過微分修正方法對初值進(jìn)行處理,可以得到精確解[16]。
狀態(tài)轉(zhuǎn)移矩陣可用于描述初始狀態(tài)的微小改變隨時間的變化。圓型限制性三體模型下,系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣Φ(t,t0) 與 Jacobi矩陣A(t) 之間的關(guān)系為式(4):
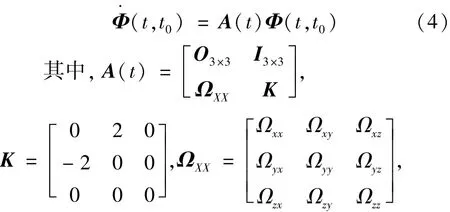
O3×3、I3×3分別為零矩陣和單位陣,ΩXX為有效勢能Ω對狀態(tài)變量的二階偏導(dǎo)數(shù)[14]。狀態(tài)轉(zhuǎn)移矩陣的初始狀態(tài)Φ(t0,t0)為單位陣,同時積分式(2)和式(4)可以得到狀態(tài)轉(zhuǎn)移矩陣Φ(t,
3 三體Lambert算法
3.1 基于牛頓-拉夫遜迭代的三體Lambert算法
為了計算目標(biāo)軌道,首先需要找到一條參考軌道。假設(shè)參考軌道的初始狀態(tài)向量為式(5):

轉(zhuǎn)移時間為Tref。以X0ref為初值,積分Tref得到參考軌道的末狀態(tài)向量如式(6):

引入?yún)⒖架壍榔钊缡剑?):
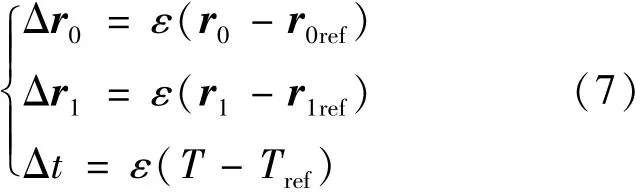
其中:0<ε≤1,r0和r1分別為目標(biāo)轉(zhuǎn)移軌道的初始和終端位置。得到新的始末位置v′0,如圖1所示。如果ε的值足夠小,則有如式(8)所示近似方程:

其中,狀態(tài)轉(zhuǎn)移矩陣Φ= Φ(0,Tref)根據(jù)參考軌道計算得到。式(8)中各項滿足式(9):
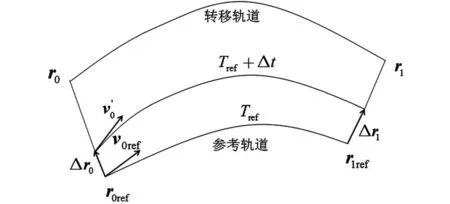
圖1 轉(zhuǎn)移軌道求解過程Fig.1 Computation process of the transfer trajectory
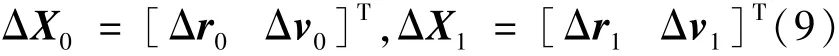
由式(8)可以得到如式(10)所示方程:

由式(10)可以得到速度的近似值如式(11):

由式(11)得到的是近似值,將狀態(tài)積分時間得到終端位置為了得到的精確值,使用式(12)所示牛頓-拉夫遜法迭代求解:

得到精確的v′0后,可以計算中間過程的轉(zhuǎn)移軌道。再將得到的軌道作為參考軌道,重復(fù)以上過程,直到轉(zhuǎn)移軌道和目標(biāo)軌道重合,即轉(zhuǎn)移軌道的初始和終端位置滿足式(13)所示約束條件

3.2 基于遺傳算法的三體Lambert算法改進(jìn)
牛頓-拉夫遜迭代法對初始值要求較高,參考軌道與目標(biāo)軌道之間差異較大時,以上經(jīng)典三體Lambert算法難以收斂。
本文提出一種利用遺傳算法尋找參考軌道的方法,使其更接近目標(biāo)軌道,然后再利用三體Lambert算法求解。參考軌道的起始位置為追蹤航天器的位置,只需求解該位置的速度增量Δv,使參考軌道的終端位置Pos′end與交會位置Posend的距離最小。同時,參考軌道的形狀應(yīng)盡可能接近Halo軌道的形狀。將參考軌道上的位置等時間離散化Pos′i,計算各離散點與對應(yīng)Halo軌道上位置Posi的距離,將這些距離的均值與終端位置的距離之和作為目標(biāo)函數(shù)。因此,設(shè)計變量為式(14):
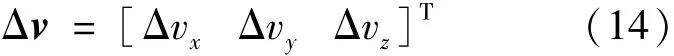
目標(biāo)函數(shù)為式(15):
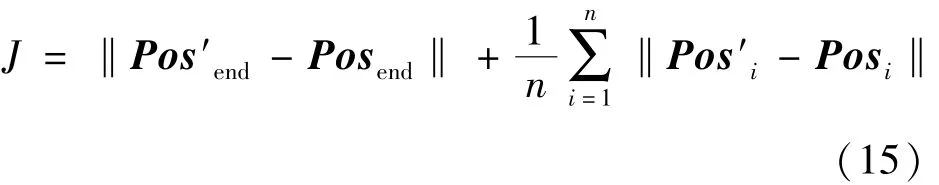
式中n為離散點的個數(shù)。利用遺傳算法求解,使J最小。把此時得到的參考軌道帶入基于牛頓-拉夫遜迭代的三體Lambert算法,即可求得目標(biāo)轉(zhuǎn)移軌道。改進(jìn)后的三體Lambert算法的求解流程如圖2所示。
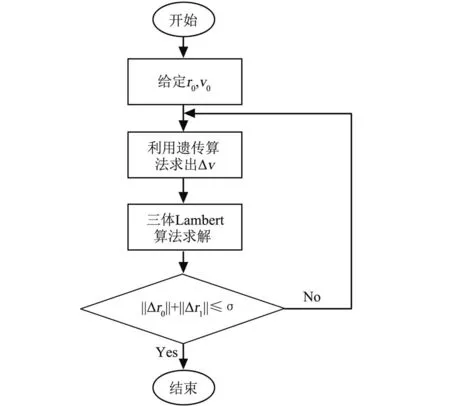
圖2 改進(jìn)后的三體Lambert算法的求解流程圖Fig.2 Flow chart of the improved three-body Lambert algorithm
4 同一Halo軌道不同相位航天器交會
設(shè)目標(biāo)航天器運行在地月系L2點一條法向幅值為Az=5×106m的北向Halo軌道上,追蹤航天器的位置為z向最小值點。當(dāng)目標(biāo)航天器與追蹤航天器的相位差分別為1°、3°、5°時,研究在不同轉(zhuǎn)移時間下的燃料消耗情況。由于相位差較小,以目標(biāo)航天器的軌道為參考軌道,利用三體Lambert算法求解。表1給出了不同轉(zhuǎn)移時間下的速度增量。圖3給出了追蹤航天器與目標(biāo)航天器相差為5°、轉(zhuǎn)移時間為7.348 2天的轉(zhuǎn)移軌道,圖4給出了圖3在xy平面的投影。由表1可以看出,在轉(zhuǎn)移時間相同的條件下,初始相位差越大,所需的速度增量越大。
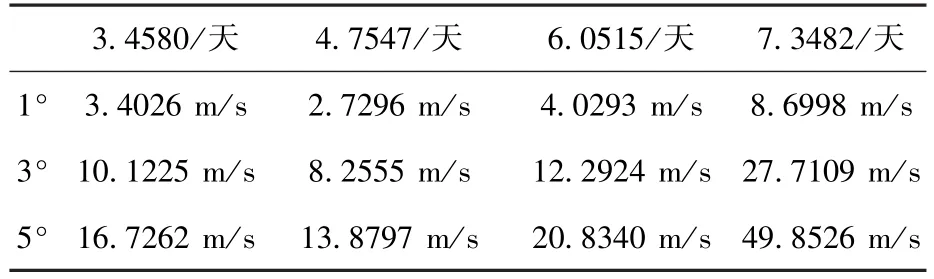
表1 不同相位差下不同轉(zhuǎn)移時間對應(yīng)的速度增量Table 1 Velocity increment of different transfer time corresponding to different phase angle

圖3 追蹤航天器轉(zhuǎn)移軌道Fig.3 Transfer trajectory of the chasing spacecraft
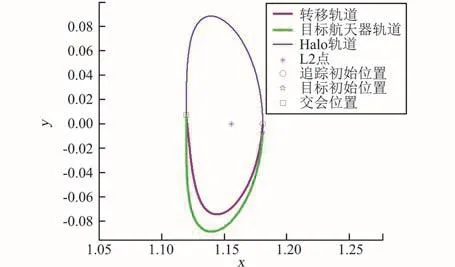
圖4 追蹤航天器轉(zhuǎn)移軌道(xy平面投影)Fig.4 Transfer trajectory of the chasing spacecraft(xyplane projection)
5 不同Halo軌道航天器交會
為了測試算法的有效性,下面研究不同Halo軌道之間轉(zhuǎn)移的情況。設(shè)目標(biāo)航天器運行在法向幅值為Az=5×106m的北向Halo軌道上,追蹤航天器分別從三條不同幅值的Halo軌道向目標(biāo)Halo軌道轉(zhuǎn)移。追蹤航天器的起始位置都位于Halo軌道z向最大值點,目標(biāo)航天器與追蹤航天器的相位差為10°,在轉(zhuǎn)移時間相同的條件下(4.322天),分別計算其所需的速度增量。參考軌道的起點為追蹤航天器所在Halo軌道上相位超前追蹤航天器10°的位置,參考軌道的終點由該Halo軌道上起點預(yù)報轉(zhuǎn)移時間得到。表2給出了從不同軌道出發(fā)所需的速度增量。圖5給出了由法向幅值為Az=1.1×107m的軌道到目標(biāo)軌道的轉(zhuǎn)移軌道,圖6給出了該軌道在xy平面的投影。

表2 從不同幅值Halo軌道出發(fā)所需的速度增量Table 2 The required velocity increment from Halo orbits with different amplitudes
從表2可以看出,在相位差和轉(zhuǎn)移時間相同的條件下,初始Halo軌道與目標(biāo)Halo軌道的法向幅值相差越大,所需的速度增量越大。

圖5 不同Halo軌道間轉(zhuǎn)移軌道Fig.5 Transfer trajectory of different Halo orbits

圖6 不同Halo軌道間轉(zhuǎn)移軌道 (xy平面)Fig.6 Transfer trajectory of different Halo orbits(xyplane)
6 長時間轉(zhuǎn)移軌道求解
經(jīng)典三體Lambert算法嚴(yán)重依賴參考軌道的性態(tài),在求解式(12)時,需要計算參考軌道狀態(tài)轉(zhuǎn)移矩陣的逆陣,如果該矩陣出現(xiàn)嚴(yán)重的病態(tài),則會出現(xiàn)迭代發(fā)散的情況。例如,計算同一Halo軌道上兩航天器交會所需的速度增量,目標(biāo)航天器運行在地月系L2點一條法向幅值為Az=5×106m的北向Halo軌道上,追蹤航天器的位置為z向最小值點。當(dāng)追蹤航天器與目標(biāo)航天器相差為5°,轉(zhuǎn)移時間為9.5095天時,直接使用三體Lambert算法求解,會出現(xiàn)迭代發(fā)散再收斂的情況,但是已嚴(yán)重偏離了參考軌道。表3給出了分別使用經(jīng)典三體Lambert算法和改進(jìn)后的三體Lambert算法計算得到的速度增量。使用改進(jìn)后的三體Lambert算法計算得到的速度增量大大減少。圖7給出了轉(zhuǎn)移時間為9.5095天時使用經(jīng)典三體Lambert算法求得的轉(zhuǎn)移軌道。圖8給出了使用改進(jìn)后的三體Lambert算法求得的轉(zhuǎn)移軌道。

表3 分別使用兩種方法得到的速度增量Table 3 Velocity increment computed by two different methods

圖7 基于牛頓-拉夫遜迭代的三體Lambert算法求解的轉(zhuǎn)移軌道(xy平面)Fig.7 Transfer trajectory computed by Newton-Raphson iteration three-body Lambert algorithm (xyplane)
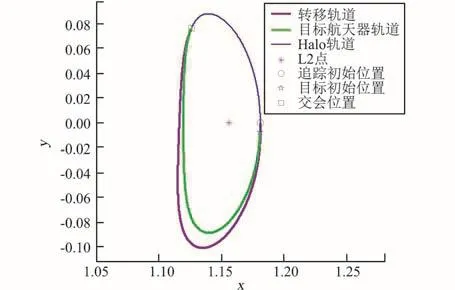
圖8 改進(jìn)方法得到的轉(zhuǎn)移軌道(xy平面)Fig.8 Transfer trajectory computed by the improved method (xyplane)
7 結(jié)論
本文利用三體Lambert算法研究了地月系L2平動點軌道交會問題,分析了同振幅不同相位交會與不同振幅交會等情況。分析結(jié)果表明,在轉(zhuǎn)移時間相同的情況下,同振幅交會的初始相位差越大,所需的速度增量越大。在滿足安全性的條件下,追蹤航天器和目標(biāo)航天器的相位差應(yīng)盡可能小。對于不同Halo軌道之間轉(zhuǎn)移的情況,在航天器相位差和轉(zhuǎn)移時間相同的條件下,追蹤和目標(biāo)軌道的法向幅值相差越大,所需速度增量越大。因此,追蹤航天器應(yīng)選擇與目標(biāo)航天器所在Halo軌道幅值相差較小的軌道作為停泊軌道。針對三體Lambert算法存在的問題,提出了利用遺傳算法求解參考軌道的方法,計算結(jié)果表明,該方法能夠有效解決長時間轉(zhuǎn)移三體Lambert算法收斂性差的問題。
本文提出的方法及分析的特性同樣適用于其他平動點軌道,可為未來平動點空間站的建設(shè)提供參考。
(References)
[1] Martin L,Shane R.The lunar L1 gateway:portal to the stars and beyond[C] //AIAA Space 2001 Conference and Expostion, Albuquerque, NM Aug.28-30, 2001.
[2] Farquhar R W.Station-keeping in the vicinity of collinear libration points with an application to a lunar communications problem[C]//AAS Space Flight Mechanics Specialist Conference, Colorado, 519-535, 1966.
[3] Canalias E,Masodemont J J.Computing natural transfers between Sun-Earth and Earth-Moon lissajous libration point orbits[J].Acta Astronautica, 2008, 63: 238-248.
[4] Koon W S,Lo M W,Marsden J E,Ross S D.Low energy transfer to the moon[J].Celestial Mechanics and Dynamical Astronomy,2001,81:63-73.
[5] 王永志.實施我國載人空間站工程、推動載人航天事業(yè)科學(xué)發(fā)展[J]. 載人航天,2011,17(39):1-4.Wang Yongzhi.Launching manned space station project and promoting the development of China’s manned space engineering[J].Manned Spaceflight, 2011, 17(39): 1-4.(in Chinese)
[6] 李明濤,鄭建華,于錫崢,等.日地平動點衛(wèi)星兩脈沖轉(zhuǎn)移軌道設(shè)計[J].北京航空航天大學(xué)學(xué)報,2009,35(7):865-868.Li Mingtao, Zheng Jianhua, Yu Xizheng, et al.Two impulses transfer trajectory design forsun-earth libration point missions[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(7): 865-868.(in Chinese)
[7] 李明濤,鄭建華,于錫崢,等.約束條件下的Halo軌道轉(zhuǎn)移軌道設(shè)計[J]. 宇航學(xué)報,2009,30(2):437-441.Li Mingtao, Zheng Jianhua, Yu Xizheng, et al.Transfer trajectory design for halo orbit with multiple constraints[J].Journal of Astronautics, 2009, 30(2): 437-441.(in Chinese)
[8] 張景瑞,曾豪,李明濤.不同月球借力約束下的地月Halo軌道轉(zhuǎn)移軌道設(shè)計[J].宇航學(xué)報,2016,37(2):159-168.Zhang Jingrui, Zeng Hao, Li Mingtao.A design method for earth-moon halo orbit transfer trajectory under different constraints to moon gravity-assisted maneuvers[J].Journal of Astronautics, 2016, 37(2): 159-168.(in Chinese)
[9] 周建平.天宮一號/神舟八號交會對接任務(wù)總體評述[J]. 載人航天,2012,18(1):1-5.Zhou Jianping.A review of tiangong-1/shenzhou-8 rendezvous and docking mission[J].Manned Spaceflight, 2012, 18(1): 1-5.(in Chinese)
[10] Sukhanov A, Prado A.Lambert problem solution in the hill model of motion[J].Celestial Mechanics and Dynamical Astronomy,2004,90:331-354.
[11] Hiday J L A, Howell K C.Impulsive time-free transfers between halo orbits[J].Celestial Mechanics and Dynamical Astronomy,1996,64:281-303.
[12] Davis K E, Anderson R L, Scheeres D J, et al.Locally optimal transfers between libration point orbits using invariant manifolds[C] //AIAA/AAS Astrodynamics Specialist Conference, Boston, USA,1998.
[13] 劉林,侯錫云.深空探測器軌道力學(xué)[M].電子工業(yè)出版社,2012:53-54.Liu Lin,Hou Xiyun.Orbital mechanics of deep space probe[M].Publishing House of Electronics Industry, 2012: 53-54.(in Chinese)
[14] 張躍東,孟云鶴,桂忱,等.Halo軌道編隊構(gòu)型重構(gòu)最優(yōu)控制研究[J].國防科技大學(xué)學(xué)報,2011,33(4):24-29.Zhang Yuedong, Meng Yunhe, Gui Chen, et al.Study on optimal control for Halo orbits formation reconfiguration[J].Journal of National University of Defense Technology, 2011,33(4): 24-29.(in Chinese)
[15] Richardson D L.Analytic construction of periodic orbits about the collinear points[J].Celestial Mechanics, 1980, 22(3):241-253.
[16] Howell K C.Three-dimensional periodic Halo orbits[J].Celestial Mechanics, 1984, 32(1): 53-71.
(責(zé)任編輯:龍晉偉)
Rendezvous Trajectory Design of Libration Points Based on Three-body Lambert Algorithm
SUN Yu1,2, ZHANG Jin1?, LUO Yazhong1
(1.College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073, China;2.The State Key Laboratory of Astronautic Dynamics, China Xi’an Satellite Control Center, Xi’an 710043, China)
V412.4
A
1674-5825(2017)05-0608-06
2016-08-15;
2017-07-27
國家自然科學(xué)基金(11402295);國防科學(xué)技術(shù)大學(xué)科研計劃項目(JC14-01-05)
孫俞,男,碩士研究生,研究方向為航天器軌道動力學(xué)。E-mail:2010027109sunyu@ sina.com
?通訊作者:張進(jìn),男,博士,講師,研究方向為航天飛行任務(wù)規(guī)劃。E-mail:zhangjin@nudt.edu.cn

