經驗模式分解與代價敏感支持向量機在癲癇腦電信號分類中的應用*

李冬梅，張洋，楊日東，陳子怡，田翔華，董楠，爾西丁·買買提，周毅,△

(1. 新疆醫科大學，新疆 烏魯木齊 830011；2.新疆醫科大學第一附屬醫院神經內科，新疆 烏魯木齊 830011；3.中山大學中山醫學院生物醫學工程系，廣東 廣州 510080；4.中山大學附屬第一醫院神經內科，廣東 廣州 510080)

1 引 言

癲癇是一種常見的慢性腦部神經疾病，其發作來源于大腦神經元異常放電，引起中樞神經系統功能短暫性失常，表現為意識、感覺等多方面功能障礙，具有不確定性、發作性，嚴重影響患者的日常生活和工作。腦電圖(electroencephalogram，EEG)的發展，對臨床試驗探測大腦皮層的腦活動和相關疾病提供了一種無創和低成本的有效技術[1]。腦電圖表示的是通過腦電電極所記錄到的各種腦電活動的總和[2]，癲癇患者的腦活動通常包括發作間期和發作期(在一些病例中存在癲癇發作的前期和后期)。從一種狀態向另一種狀態演變時，腦電信號會發生變化，大腦系統與此對應的各種動力學特征向量也隨之產生變化[3]。腦電信號具有非平穩性和非線性特征，因此,對于腦電信號分析往往以傳統的時域、頻域或者時頻結合的方法為主[4-7]，通過計算各種非線性的特征值來區分腦電信號[8]。大多數的數據預處理方法均是用小波變換對信號進行分解，而分層數、基函數的選擇對結果有很大影響，不具備對信號自適應的分解能力[9-10]。

對癲癇腦電信號進行自動檢測與識別的分類方法越來越多，主要有支持向量機(SVM)、決策樹(DT)、隨機森林(RandomForest)、模糊分類(FM)等。我們采用了代價敏感支持向量機(cost-sensitive support vector machine,CSVM)這一方法，其不僅具備了支持向量機(support vector machine，SVM)的特征，并且能夠考慮到樣本的不同誤分類代價，實現代價敏感挖掘。本研究中，首先采用EMD算法將癲癇腦電數據進行分解，選取主要IMF分量，計算樣本熵；使用核函數為RBF(rial basis function，RBF)的代價敏感支持向量機進行分類，先選取一例患者的腦電信號作為訓練數據對分類器進行訓練，然后選取不同的病例腦電信號作為測試數據進行分類，并使用K-CV(k-fold cross validation，K-CV)算法進行參數尋優，最后依據臨床醫師診斷得出分類結果。用這種測試方法不僅可以進一步提高分類的準確率，并且能對分類器的泛化能力和學習能力進行更準確的描述，對于臨床上研究癲癇實時信號檢測與識別更具有實際意義。

2 數據處理及特征提取

2.1 經驗模式分解算法

EMD(empirical mode decomposition，EMD)是一種自適應信號時頻分析方法，在處理腦電信號這一類非平穩非線性隨機信號上具有明顯的優勢[11]。它可將信號分解成一系列的準單分量信號，即本征模函數(intrinsic mode function，IMF)。每一階IMF包含了原始信號的不同頻率信息，分析這些IMF即可獲得信號的局部信息特征。

經驗模式分解是由Huang等人提出的一種新的自適應信號時頻處理方法，其本質是通過信號的時間尺度獲得本征波動模式。EMD有三大假設[12-13]：(1)信號至少有一個極大值點和一個極小值點；(2)特征時間尺度由極值點的時間推移定義；(3)如果整個信號只包含曲折點而不包含極值點，可以先微分一次或者多次找到極值點，然后將所得到的分量進行積分得到最后結果。這樣任何一個復雜信號都可以被分解成有限個具有物理意義的固有模態函數(IMF)，其中任何一個IMF滿足以下兩個約束條件：

(1)數據段內，極值點和零點數目要想等或者最多相差1；

(2)任何一點處，分別由局部極大值點和局部極小值點確定的包絡線的均值為0。

EMD的具體步驟是：

(1)求出信號C(t)所有的極值點，并分別用一條光滑的曲線連接，使得兩條曲線間包括所有的信號。上下包絡線emax(t)和emin(t)的均值記作m1(t)，求出：

C(t)-m(t)=h1(t)

(1)

若h1(t)是一個固有模態分量，那么h1(t)就是C(t)的第一個分量。

(2)用h1(t)替代C(t)，重復之前的步驟，直到h1k(t)為一個IMF，記C1(t)=h1k(t)，并將C1(t)從信號C(t)中分離出來，得到：C(t)-c1(t)=r1(t)，并令C(t)=r1(t)；

(3)重復上述步驟，直到rN(t)或c1(t)滿足預設條件，C(t)的分解結束。

一般來說，EMD分解出來IMF的前幾個分量集中了原始信號中的主要信息。將EMD分解應用到腦電分析中，可為研究人員提供有價值的信息，避免了人為因素的干擾，更有利于提高腦電信號的分類準確率。

2.2 樣本熵

EEG信號是一種非線性時間序列。常見的非線性動力學參數有關聯維數、Lyapunov指數、近似熵、樣本熵等，其中樣本熵(sample entropy，SampleEn)是由Richman和Moornan提出的一種新的時間序列復雜性測度方法。可用于測量兩個新信息發生的條件率。樣本熵是一種與近似熵類似，但精度更好，可降低近似熵的誤差。其具體算法如下：

設原始數據為x(1)，x(2)，…，x(N)，共N點。

(1)按序號連續順序組成一組m維矢量：

X(i)=[x(i)，x(i+1)，…，x(i+m-1)]，i=1～N-m+1

(2)

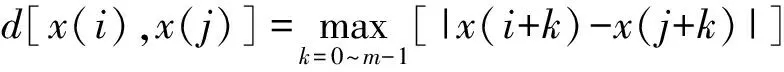
(3)

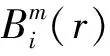
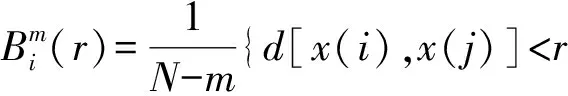
(4)

(5)

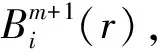
(6)理論上此序列的樣本熵為：

(6)

當N為有限值時上式表示為：

SampEn(m，r，N)=-ln[Bm+1(r)/Bm(r)]

(7)

SampEn的值顯然與m，r的取值有關。不同的嵌入維數m和相似容限r對應的樣本熵也不同。在一般情況下m=1或2,r=0.1SD～0.25SD(SD為標準差)計算得到的樣本熵具有較為合理的統計特性，故本文所有樣本熵的計算均取m=2，r=0.25SD。

大腦在癲癇發作時，神經元同步放電，各種腦功能都受到不同程度的抑制，因此與正常腦電活動相比，復雜度會有所降低。癲癇患者從發作間期到發作期，樣本熵會有不同程度的下降，發作期結束后樣本熵又會逐漸升高。

2.3 代價敏感支持向量機(CSVM)

傳統分類算法通常假定每個樣本的誤分類具有同樣的代價且每類樣本數大致相等。但是現實的數據挖掘中這種假設是不成立的，因此取得的結果也不理想。考慮到不同樣本的誤分類具有不同的代價，提出代價敏感支持向量機(CSVM)的方法，對樣本的錯分采用不同的懲罰參數重新構造分類器，使其具有代價敏感的特性。

假設正常腦電為正類，癲癇腦電為負類。本研究對于正負類的訓練錯誤引入不同的懲罰參數C+和C_對支持向量機進行訓練，具體算法如下：

在訓練集中T={(x1，y1)}，…，(xl，yl)}∈(X×Y)lxi為輸入出樣本，yi為輸出樣本，其中，xi∈X=Rn，yi∈Y={-1,1}，i=1，…，l。

選取徑向基核函數(gaussian radial basis function,RBF)，其形式為：

K(xi，xj)=exp(-‖xi-xj‖2/σ2)

(8)

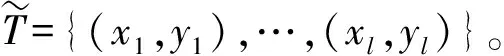
選取懲罰參數，構造并求解最優問題：

subject toyi((ω·xi)+b)≥1-ξi，ξi≥0，i=1，…，l

(9)

根據Lagrange函數，得到對偶問題：

0≤αi≤C+，i=1，2，…，l：yi=+1

0≤αi≤C-，i=1，2，…，l：yi=-1

(10)

(11)

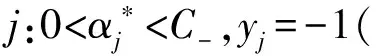
f(x)=sgn((ω*·x)+b*)

(12)

3 實驗結果與分析

3.1 臨床數據采集

實驗數據來自于新疆醫科大學第一附屬醫院神經科腦電圖室，采樣頻率均為200 Hz。采用新疆醫科大學第一附屬醫院神經科腦電圖室某六位顳葉癲癇患者的數據，對六例患者的腦電數據描述如下：一例16歲顳葉患者(1號)的腦電數據診斷為發作間期118段與發作期118段，每段1500點數據；一例22歲顳葉患者(2號)的腦電數據發作間期至發作期330 s，共110段數據，每段1 500點數據、代表時間3 s，其中臨床診斷在150～230 s為發作期，患者表現為左側上肢抽搐；一例46歲顳葉患者(3號)的腦電數據發作間期至發作期160 s，共80段數據，每段1 000點數據、代表時間2 s，其中臨床診斷在105～142 s為發作期，患者表現為雙上肢自動癥、口咽部自動癥；一例28歲顳葉患者(4號)的腦電數據發作間期至發作期200 s，共100段數據，每段1 000點數據、代表時間2 s，其中臨床診斷在85～126 s為發作期，患者表現為失神、左上肢自動癥、口咽部自動癥；一例39歲顳葉患者(5號)的腦電數據發作間期至發作期160 s，共80段數據，每段1 000點數據、代表時間2 s，其中臨床診斷在95～116 s為發作期，患者表現為咀嚼、左上肢強直、右上肢自動；一例15歲顳葉患者(6號)的腦電數據發作間期至發作期160 s，共80段數據，每段1 000點數據、代表時間2 s，其中臨床診斷在105～136 s為發作期，患者表現為愣神、雙上肢自動癥。實驗采用數據均為頭皮腦電數據，采集后由臨床腦電圖儀進行預處理后存儲于醫院數據庫中，因此可直接將其進行研究。

3.2 實驗過程

基于EMD的數據分解及特征值分類、發作預測的過程見圖1。對輸入信號首先進行EMD分解；對得到各階的IMF分量進行傅里葉變換從而獲得頻譜能量；計算特征值，從中選擇合適的特征向量作為分類器的輸入，進行分類，并對分類器進行參數優化，最后可以得到較為理想的分類結果。

圖1基于EMD分解的特征提取及分類優化過程

Fig1EMDdecompositionbasedonfeatureextractionandclassificationoptimizationprocess

首先，利用1號患者的發作間期與發作期各118段數據進行特征提取，將得到的236個樣本熵值輸入到分類器構建算法中得到分類器。之后將剩余的5位患者腦電數據按順序各分為兩組，輸入到構件號的分類器中進行分類，得到分類結果。

3.3 實驗結果分析

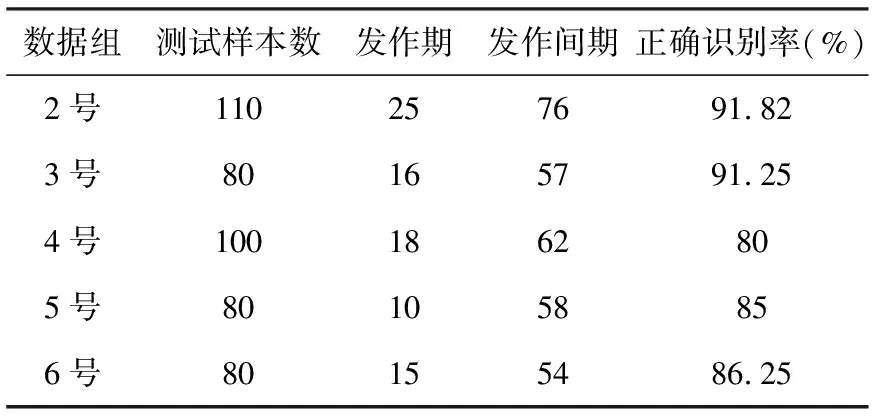
由于記錄數據時數據量較大，因此結合統計學的關聯性分析，只選取關聯性較小的導聯數據進行分析。對6例患者的腦電數據樣本進行經驗模態分解，并對IMF分量做傅里葉變換，得到頻譜，主要頻譜能量集中在前三個IMF，因此提取前三個IMF分量的特征值。將已經得到的特征值樣本利用CSVM分類器對其進行分類實驗，其中核函數為徑向基(RBF)函數，懲罰參數取c=1，核函數參數取g=0.01。信號分類實驗結果見表1。

通過對訓練樣本集進行訓練，得到分類模型后，利用測試集樣本對分類器進行檢驗，得到的準確率反應了分類器的分類效果，但這種效果只關注了經驗風險，因此這種評價有不足之處。為了量化地表示CSVM的學習能力和泛化能力，采取了交叉驗證(cross validation，CV)中K-CV的方法對分類器的性能進行驗證。K-CV可以有效地避免過學習以及欠學習狀態的發生，最后得到的結果也比較具有說服力。

表1 5位受試對象IMF能量譜特征提取方法分類結果

Table1No. 1subjectsoftheIMFenergyspectrumfeatureextractionmethodclassificationresults

數據組測試樣本數發作期發作間期正確識別率(%)2號110257691.823號80165791.254號1001862805號801058856號80155486.25

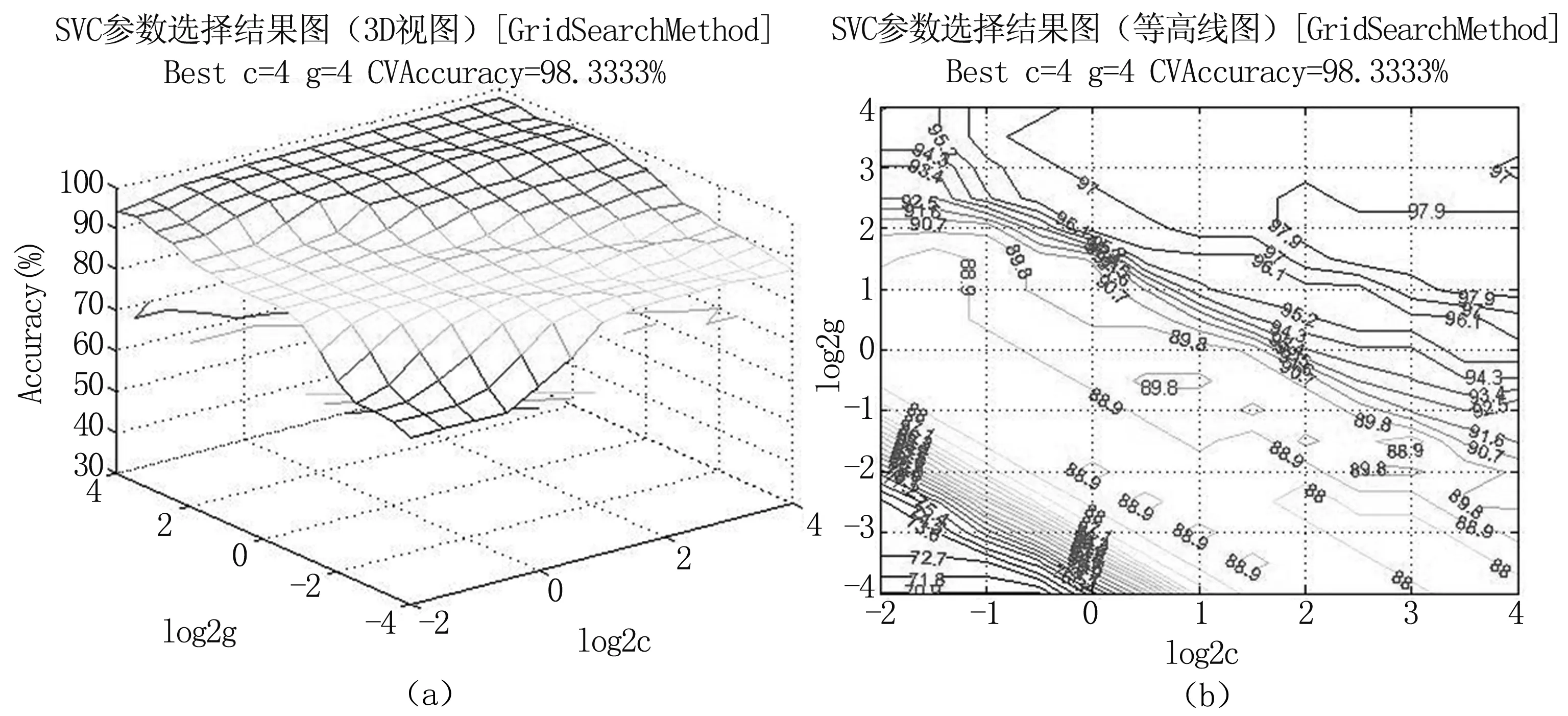
圖2 SVC參數尋優

取2號患者數據對分類器的訓練情況進行分析。圖2是在網格搜索下的參數c和g的不同取值所對應的分類準確率所對應的3D視圖及其等高線圖。圖中x軸表示c取以2為底的對數后的值，y軸表示g取以2為底的對數后的值，等高線表示的取相應的c和g后對應的K-CV方法的準確率，通過圖中可以看出把c的范圍縮小到2＾(-2)～2＾(4)，同時g的范圍可以縮小到2＾(-4)～2＾(4)，這樣在上面粗略參數選擇的基礎上可以再利用SVMForClass進行精細的參數選擇。

表3為5位受試者的樣本分類效果比較。與經驗參數下分類效果進行比較，可以看出在參數優化后，分類器的分類準確率有了明顯提高。

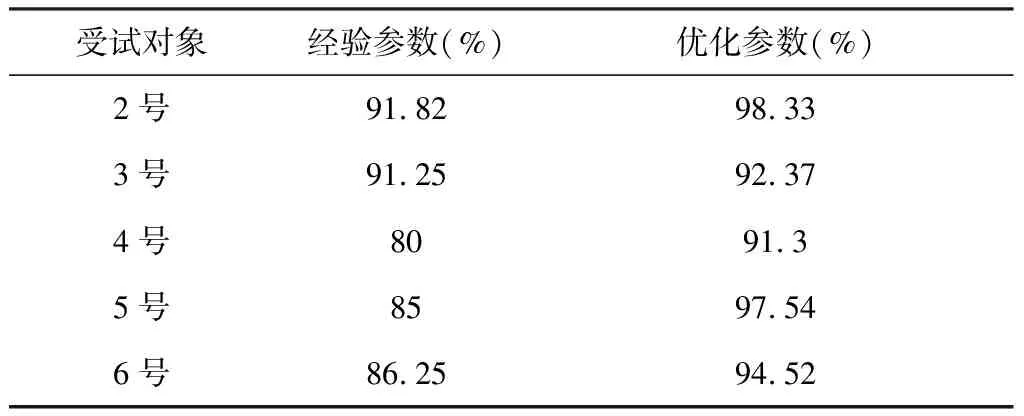
表3 受試者腦電數據在兩類分類器下的準確率

4 總結與展望

本研究表明，選取EMD對數據進行分解處理時，在一定程度上克服了傳統腦電算法處理不具備自適應性信號處理的能力；并針對傳統分類算法中假定每個樣本的誤分類具有同樣的代價且每類樣本數大致相等的缺陷，提出了代價敏感支持向量機的方法，在分類器進行設計時，考慮樣本的不同誤分類代價，從而實現代價敏感挖掘；對以構建好的分類器進行參數優化，進一步提高了分類的準確率，較真實地反應了分類器的學習能力和泛化能力。

目前，神經科學的研究已成為生命科學研究的熱點。基于非線性動力學的方法，通過對神經電信號的研究，定量描述腦電信號的某些特征，能夠對癲癇類神經疾病進行更加深入的探索研究。本研究利用經驗模式分解(EMD)在對非平穩時變信號進行多尺度分解，將代價敏感支持向量機運用于癲癇腦電信號的分類，并對分類器進行優化，不僅可以提高臨床上癲癇腦電信號的檢測與識別的準確率，還可用于實時監測的在線分析，更好地幫助電生理醫生客觀準確地分析腦電信號，為后續癲癇病的研究提供基礎。