圓錐曲線參數方程在高中數學解題中的應用

孫丹丹

(淮安市新馬高級中學，江蘇 淮安 211700)

圓錐曲線參數方程在高中數學解題中的應用

孫丹丹

(淮安市新馬高級中學，江蘇 淮安 211700)

本文對圓錐曲線參數方程在高中數學解題中的實際應用情況進行詳細分析和研究，為學生學習成績的提升打下良好的基礎，提高學生的數學解題思路以及解題質量.

圓錐曲線參數方程、高中數學、解題、應用

數學本身就是一門比較復雜的學科，數學知識具有一定的抽象性和復雜性，學生學習起來比較困難，特別是對于高中生來說，更是如此.圓錐曲線方程是高中數學學習過程中非常重要的知識點之一，在高考當中占據的比重也比較大.在圓錐曲線定義當中，利用橢圓定義以及雙曲線的具體定義，能夠幫助學生更好地對數學問題進行解答.

一、利用圓錐曲線方程解決最值問題

傳統數學學習方式主要是通過廣泛的做題，對數學題型進行反復地訓練，來達到強化學生記憶的目的，這樣才能夠保證學生自身的學習成績能夠不斷提升.在實際教學過程中，針對學生學習能力以及學習進度問題，通過對一些典型習題的設計和應用，注重學生思維思考模式的培養，讓學生能夠養成舉一反三的意識，這樣不僅能夠從根本上加強學生對于數學的感知能力，而且能夠促使高中生的數學學習成績有效提升.

根據這道題目當中給出的條件，教師要引導學生在對這道問題進行解答的時候，不能夠局限其自身的思維，要敢于想象.教師要引導學生將這道題目當中涉及的知識與其他知識之間進行有效的銜接，幫助學生找到解題思路.

解析根據題目可以設A(acosθ,bsinθ)，通過對四邊形的觀察，可以得到其四邊與坐標軸分別保持平行狀態，在這種條件下，可以推斷四邊形ABCD為矩形，其面積可以表示為S=4(acosθ×bsinθ)=2absin2θ.當S表示為最大值的時候，sin2θ是最大值，其值為1.當sin2θ=1的時候，S=2ab.四邊形ABCD的周長可以表示為L=4(bsinθ+acosθ)=4(a2+b2)1/2sin(θ+β)，其中sinβ=a÷(a2+b2)1/2，cosβ=b÷(a2+b2)1/2.當sin(θ+β)為最大值1的時候，四邊形的周長為最大.sin(θ+β)的值為1時，Lmax=4(a2+b2)1/2.

二、利用定義與正余弦定理求焦點三角形

在學生實際解題過程中，要培養學生發揮其自身的探索性思維，通過總結與小組合作的模式，從根本上提高學生的數學解題思維和能力.數學習題當中單一性的題目相對來說比較少，基本上都是與一些其他知識復合型的出現，難度系數也越來越高，這對學生的解題能力要求就比較高.

在本題中,根據基礎知識，利用定義的深入了解和認識.通過正余弦定理，將面積公式與正余弦定理進行結合，能夠得到準確的答案.

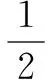
(1)

(2c)2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cosθ

(2)

通過與圓錐曲線中雙曲線的定義能夠得到

|PF1|-|PF2|=2a，

|PF1|2+|PF2|2-2|PF1|·|PF2|=4a2.

(3)

從而完成這道問題的解答.

三、圓錐曲線參數方程解題中應當注意的問題

在教學過程中，教師不僅要讓學生能夠深入地掌握一些理論性的知識或者是具體公式的用法，而且要讓學生意識到如何將這些知識和公式與實踐題目進行有效結合.在這種形勢下，針對圓錐曲線參數方法方程的相關知識，教師要讓學生多寫、多練、多問、多記，讓學生能夠為日后的解題打下良好的基礎.這樣不僅能夠幫助學生摸清題目的內涵，讓學生在遇到數學問題時，能夠了解其中所要表達的意思，完成快速有效的解題.

綜上所述，高中數學在高中教育當中占據非常重要的地位，對學生高考也產生非常重要的影響.因此，在高中數學教學活動實施過程中，教師要注重對學生理論知識的強化，讓學生能夠將理論知識切實有效地應用到實踐當中，這樣不僅能夠提高學生對于數學知識題目的理解力，而且能夠鍛煉學生舉一反三的能力.通過對一些典型題目的講解，能夠促使學生解題思維以及解題質量的有效提升.

[1]毛芹.圓錐曲線參數方程在高中數學解題中的應用[J].理科考試研究：高中版，2014(21).

[2]陳榮明.直線參數方程教學設計[J].教學月刊：中學版，2011(23).

[3]李淑燕.用圓錐曲線的參數方程解題例談[J].數理化學習：高三，2011(07).

G632

A

1008-0333(2017)22-0012-02

2017-06-01

孫丹丹(1985.1- )，女，吉林公主嶺市人，中教一級，本科學歷，從事高中數學教學.

責任編輯：楊惠民]