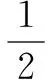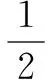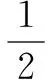利用主元法處理函數中的不等關系的有效途徑
蔡自力
(廣東省韶關市廣東北江中學,廣東 韶關 512026)
利用主元法處理函數中的不等關系的有效途徑
蔡自力
(廣東省韶關市廣東北江中學,廣東 韶關 512026)
構造函數借助導數研究函數的的性質,進而解證不等式是近幾年全國高考壓軸題的熱點與難點.這類問題往往涉及到多個變量和參數,我們可以嘗試選擇其中一個字母作為研究的主要對象看作是主元,而將其余各字母視作參數或常量,然后構造函數,借助導數可以找到解題的思路.本文擬從幾個教學實例出發,探討如何利用主元法處理函數中的不等關系的有效途徑.
主元法 ;不等關系;途徑
構造函數,借助導數研究函數的性質,進而解證不等式是近幾年全國高考壓軸題的熱點與難點.這類問題往往涉及到多個變量和參數,如何構造易于求導和求最值的函數是決定成敗的關鍵.
事實上,這類問題可選擇其中一個字母作為研究的主要對象看作是主元,而將其余各字母視作參數或常量,然后構造函數,借助導數可以找到解題的思路.本文擬從幾個教學實例出發,探討如何利用主元法處理函數中的不等關系的有效途徑.
一、用變量為主元,替換參數,構造輔助函數
處理含參數的函數不等式相關問題,通過審題,可嘗試找到參數與變量之間的關系式,實施換元,通過構造新函數使問題獲解.
例1 (2009全國卷Ⅱ理第22題)設函數f(x)=x2+aln(1+x)有兩個極值點x1、x2,且x1 (Ⅰ)求a的取值范圍,并討論f(x)的單調性; 分析在第(Ⅱ)問中,直接計算f(x2)是很難證出結果的,若能想到用x2表示a實施換元,則問題可迎刃而解. ⑴當x∈(-1,x1)時,f′(x)>0,∴f(x)在(-1,x1)內為增函數; ⑵當x∈(x1,x2)時,f′(x)<0,∴f(x)在(x1,x2)內為減函數; ⑶當x∈(x2,+)時,f′(x)>0,∴f(x)在(x2,+)內為增函數. 則h′(x)=2x-2(2x+1)ln(1+x)-2x=-2(2x+1)ln(1+x). ⑵當x∈(0,+)時,h′(x)<0,∴h(x)在(0,+)單調遞減. 例2 函數f(x)=aln(x2+1)+bx,g(x)=bx2+2ax+b,(a>0,b>0).已知方程g(x)=0有兩個不同的非零實根x1,x2. (1)求證:x1+x2<-2; (2)若實數λ滿足等式f(x1)+f(x2)+3a-λb=0,求λ的取值范圍. 分析(1)用判別式和韋達定理易解 (2)由第(1)問知,x1+x2,x1x2均可用a,b來表示,故可考慮用a,b為主元. 解(1)由g(x)=bx2+2ax+b=0方程有兩個不同的非零實根, (2)由(1)知x1x2=1. 因此λ>2ln2+1. 例3 (湖南省2017屆十三校聯考第一次考試理科數學試卷第22題第(3)問) 已知函數f(x)=x2-2x+alnx(a>0).若函數f(x)有兩個極值點x1、x2(x1 令f′(x)=0?2x2-2x+a=0.又∵函數f(x)有兩個極值點x1、x2(x1 ∴2x2-2x+a=0有兩個不等實數根x1、x2(x1 例4 (四川省資陽市2017年高考模擬考試數學理第22題第2問) 已知函數f(x)=ln(x+1)+ax,對任意x2≥e,x1>0,存在x∈(-1,+),使>成立,求實數a的取值范圍. 設p(x)=-f(x)-a,即p(x)=-ln(x+1)-ax-a, 當a≥0時,p(x)為(0,+)上的減函數,且其值域為R,可知符合題意. (Ⅰ)討論函數y=f(x)的單調性; 分析第(Ⅱ)問含有a,λ,x1,x2四個字母,據題意需要建立關于λ的函數,因含有絕對值,故先去絕對值符號,又實數a有范圍,不妨嘗試將a設為主元,再設法將λ與x進行變量分離. 解(Ⅰ)過程略,結論為 當a=0時,函數f(x)在區間(0,+)上單調遞增; 當a>0時,函數f(x)在區間(0,1)和(2a+1,+)上分別單調遞增,在(1,2a+1)上單調遞減. 則g(x)在[1,2]上單調遞增, 化簡得x2-(2a+2)x2+(2a+1)x+λ≥0, 所以只需(2x-2x2)2+x3-2x2+x+λ≥0, 即x3-6x2+5x+λ≥0對任意的x∈[1,2]恒成立.令h(x)=x3-6x2+5x+λ,x∈[1,2], 顯然,h′(x)=3x2-12x+5<0在[1,2]上恒成立, 所以,函數h(x)在[1,2]上為減函數, 所以,只需h(x)min=8-24+10+λ≥0,得λ≥6. 所以λ的取值范圍是[6,+). 眾所周知,在處理函數不等式時,經常會受到多變量的困擾,只要我們認真審題,選準其中某個變元為主元,逐步消元,多次構造函數層層推進,就可以達到排除字母間的干擾,簡化問題結構最終使問題獲解的目的. [1]張奠宙,過伯祥.數學方法論稿[M].上海:上海教育出版社,1996. [2]陶華君.構造函數在解題中的應用[J].高中數學教與學,2011. [3]劉良華.數學構造思想方法的探索與實踐[D].華中師范大學,2004. G632 A 1008-0333(2017)22-0015-03 2017-06-01 蔡自力(1962.9-),男,漢族,湖南省懷化人,中學數學高級教師,本科學士,特級教師,主要研究高中數學教育教學. 責任編輯:楊惠民]




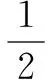



二、多變量問題,可將一個變量視為主元,構造輔助函數









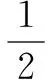














三、當參數與變量均給出取值范圍時,可考慮將參數視為主元,嘗試變更主元法