三角函數最值問題解題方法探究

張成中

(云南省富源縣第四中學,云南 曲靖 655503)

三角函數最值問題解題方法探究

張成中

(云南省富源縣第四中學,云南 曲靖 655503)

本文主要介紹了配方法、單調性法和換元法解決三角函數最值問題.

三角函數最值；配方；單調性；換元

三角函數最值問題是三角函數知識的綜合應用，具有很強的靈活性，其一直也是高考的重點，所以學生在高考復習時，對于這類問題應打起十二分的注意，掌握多種方法解決此類問題非常有必要.

一、配方法求三角函數最值

通過配方法解決三角函數問題是高考中的重要考點，通過對所求的三角函數進行恒等變形，將原函數轉化為完全平方式，進而求出函數最值.配方法是求三角函數最值的重要方法，這種方法思路清晰，簡潔明了.下面的例子就是通過配方法求三角函數最值的典型例題.

例1 求三角函數y=5sinx+cos2x的最值.

分析此題中的三角函數是由sinx和cos2x組成，通過函數圖象或者求導都無法得到函數的最值.但是通過對函數進行恒等變形，將問題轉化為二次函數在特定區間內求最值，那么題目自然迎刃而解.

評注本題如果用常規的求導法求解，求解過程會非常繁瑣，此時明智的做法是通過恒等變形，將原三角函數式進行轉化，將原函數轉化為完全平方式，以熟悉的函數為載體來求最值，可以使得解題過程大大簡化，方便求解.

二、單調性法求三角函數最值

通過單調性法來求函數最值是一種普遍方法.這種方法在求三角函數最值時也同樣適用，通過判斷三角函數在對應區間上的單調性，可以很快地求出函數最值.

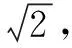
評注對于本題，不能被題目中的函數形式所迷惑而使用基本不等式法，應該認真審題，避開陷阱，采用單調性法來解答此題.

三、換元法求三角函數最值

通過換元法求三角函數最值是高考中的熱點，對于此類三角函數問題，一般采用局部換元的方法，將原函數轉化為代數函數，再通過求導法求出函數最值.這種方法思路清晰，自然便捷，是一種不可多得的好方法.

分析本題中的函數含有兩個三角函數乘積，直接求解非常麻煩.但是若能通過換元法，將三角函數問題轉化為代數問題，然后通過求導法，判斷函數的單調性，通過研究函數的單調性，即可求出未知函數的最大值.

綜上所述，本文通過多種方法研究了三角函數最值問題，學生在高考復習中應該多下功夫，只有對這些方法全部熟練掌握，才能打贏高考復習攻堅戰，在高考中遇到三角函數的最值問題才能胸有成竹、得心應手.

[1]胡進.基于不等式在高中數學教學中的應用[J].中學生數理化,2014(08).

[2]張志剛.探討三角函數解題思路與方法[J].理科考試研究,2014(02).

G632

A

1008-0333(2017)22-0040-02

張成中(1981.03-)，男，云南富源，中學一級，本科，從事高中數學教學.

責任編輯：楊惠民]