對初中課堂教學數學建模的思考
梅婷
【摘要】作為站在三尺講臺上的教師越來越重視對數學的建模理念,因為數學建模能夠有效地引導學生的數學學習過程,所以悉心研究數學建模是時代賦予教師的使命。本文結合多年來的教學實踐,談談對初中課堂教學數學建模的一些思考,僅作當今初中數學課堂教學的拋磚引玉。
【關鍵詞】數學建模;實踐思考
數學建模理念緊隨時代而不斷深化,在課堂教學過程中有效地進行數學建模是大勢所趨。通過課堂上的數學建模,一方面能夠使學生用數學的眼光看待熟悉的情境,讓數學走進生活,從而驅動學生探究數學的興趣,另一方面還能夠培養學生的數學應用意識,同時還能夠使學生在應用數學的思維方法中形成創新意識、分析和解決實際問題的能力。
一、在初中課堂教學中數學建模真正能夠讓學生在數學中揭示生活,在生活中發現數學
1.數學建模能夠驅動學生探究數學的潛能
數學建模是學習數學知識的一種新的有效方式,為學生提供了一套自主探究的思路,方便他們在實際問題中體驗數學的解決方法的妙用。讓學生在學習過程中有“模”可依,有“模”可行,形成適宜于自己的數學思維。所以,數學建模成為學生思考實際問題的套路,能夠在陌生的環境中找到分析解決問題的方法,因此,數學建模能夠驅動學生探究數學的潛能。
2.數學建模是對學生的應用意識的一種創新思考
沒有數學建模,很多學生對繁、難的數學認識不足,更不會深入到生活,走入純數學的死胡同,感到數學的學習是登天之事。其實數學就是服務于生活、生產的,將數學知識的應用到社會中去就可以更好地提高生產效率和改善生活質量。因此,數學建模是中學不可缺失的任務。它不但體現了數學的精神,而且體現了數學的思想和方法。在初中課堂上數學建模,可以說是對學生的應用意識的一種創新思考。
二、挖掘出初中教學過程中常見的幾種數學建模,揭示數學知識的真正內涵,讓學生在循規蹈矩中提升學科素養
1.數學建模一——方程及方程組
方程及方程組是一種最為普遍的對一些數量關系最基本的數學建模,針對需要解決的實際問題設定相應的未知數,再通過數量關系列出相等的代數式,當然還有重要的環節就是得出結果之后需要驗證其是否符合實際問題的意義。
例如:學校車棚內停放小轎車和電動自行車共100輛,而車輪胎共262個,小轎車和電動自行車各多少輛?
要讓學生有問題意識,題目需要回答的是“小轎車和電動自行車各多少輛”,就可以設它們分別是x、y輛,也可以考慮設小轎車是x輛,它與電動自行車共為100輛,電動自行車即為(100-x)輛。所以說,方程及方程組的數學建模就是一種問題意識的建模。
2.數學建模二——不等式
不等式表達的是一種數量不等關系,人們總是用一種具體的數值去揭示模糊的問題,或者是用一個模糊的區域表達一個固定的范圍的關系。因此,解決問題只能是問題中某個量的變化范圍,這就是數學的不等式建模。
例如:某牛奶每聽2.5元。每次銷售8萬聽,設每聽提價0.10元,銷售量就減少2千聽,要使每次銷售總收入不低于15萬元,求每聽牛奶最高提價為多少?
解決的實際問題是求出每聽牛奶的最高提價,這就是一種模糊問題。怎樣才能找到模糊的數量關系,重要的是對“設每聽提價0.10元,銷售量就減少2千聽”的理解,可以用比例關系來思考:“設每聽提價0.10x元,銷售量就減少2x千聽”,從而找到不等式的關系。
3數學建模三——幾何
幾何建模是數學中的數形轉換的思想,是數學的基本思維方法。在生活中這種數學建模無處不在,如航空航天、導彈的打擊與攔截、房屋的建造、鐵路涵洞的設計、天氣預報……這些都離不開幾何問題分析。
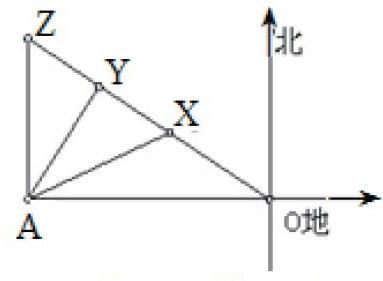
例如:近期我國南方受寒潮的影響普遍降低溫度8~12℃,若目前寒潮中心在O地,其中心以25km/h的速度向西北方向移動,其中心180km的范圍內都會受寒潮的影響,A市位于O地的正面方向230km處,問A市是否會也會降溫?若降溫,影響的時間為多長?
這是真實的生活實際問題,通過數形轉換可以發現轉化為直角三角形就可以找到方法。首先通過直角三角形的關系計算出AX的距離,而后比較得:AX<180,確定會受此次寒潮影響;再根據三角形的特征計算出XZ的距離,就可求出寒潮持續的時間。
另外,在初中數學中還有很多數學建模的思想,如函數、模糊數學等等,這里就不再一一細說了。
總之,數學建模是對數學思維方法的一種固定化的建構,是對學生形成數學思想的一種有效建構。在課堂上學會了數學建模,學生在生活中就能夠順理成章地應用數學思想去積極思考問題、解決問題。毋庸置疑,數學建模仍然是一個宏偉的工程,需要我們每一個站在三尺講臺的教師去細心打造,去精心實踐。

