基于ECC的支持標簽所有權轉移的RFID認證協議

楊興春，許春香，李朝榮

(1.電子科技大學 計算機科學與工程學院，成都 611731； 2.四川警察學院 計算機科學與技術系，四川 瀘州 646000；3.宜賓學院 計算機與信息工程學院，四川 宜賓 644000)

(*通信作者電子郵箱Yangxc2004@163.om)

基于ECC的支持標簽所有權轉移的RFID認證協議

楊興春1,2*，許春香1，李朝榮3

(1.電子科技大學 計算機科學與工程學院，成都 611731； 2.四川警察學院 計算機科學與技術系，四川 瀘州 646000；3.宜賓學院 計算機與信息工程學院，四川 宜賓 644000)

(*通信作者電子郵箱Yangxc2004@163.om)

針對射頻識別(RFID)標簽認證及其所有權轉移過程的隱私泄露等安全問題，以及認證協議通常與標簽所有權轉移協議單獨設計的現狀，基于支持橢圓曲線加密(ECC)的標簽，提出了一個適用于開放環境的兼具標簽認證和所有權轉移的協議。該協議結構類似于Diffie-Hellman密鑰交換算法結構，協議的標簽隱私保護基于橢圓曲線上的計算性Diffie-Hellman問題的難解性。經證明，該協議滿足標簽隱私保護要求及認證協議的其他安全需求。與近年來其他基于標簽支持ECC的RFID認證協議相比，從支持標簽所有權轉移、標簽計算開銷、協議通信開銷和標簽隱私保護等多方面綜合評估，所提出的認證協議優于對比協議。另外，針對較安全的應用場合，給出了閱讀器單向認證標簽的簡化版協議。

射頻識別；認證協議；標簽；所有權轉移；橢圓曲線加密

0 引言

射頻識別技術(Radio-Frequency Identification，RFID)作為物聯網的主要技術之一，目前已廣泛應用于工業和商業領域，如智能控制、車載物聯網、供應鏈管理、門禁訪問控制、智能醫療管理等。一個典型的RFID應用系統由標簽(Tag)、閱讀器/查詢器(Reader/Interrogator)、后臺服務器(Back-end Server)組成。基于制造成本考慮，標簽的計算能力和存儲能力有限。根據芯片供電來源，標簽分為三類：有源標簽、無源標簽和半有源標簽。有源標簽由芯片集成電池供電，可主動發送信號，通信距離較長。無源標簽內置線圈天線，靠閱讀器發送的射頻能量供電，因而其通信距離有限。半有源標簽在休眠狀態時由集成于芯片的電池供電，以維持芯片電路所需能量；當與閱讀器通信時，靠閱讀器發送的射頻能量供電。閱讀器具有較強的計算能力，用于查詢標簽并轉發收到的標簽信息至后臺服務器。后臺服務器有很強的計算能力和存儲能力，用于檢索/盤點標簽及其所附著物品的信息。RFID系統典型結構如圖1所示。

對標簽的認證是RFID系統的基本功能。標簽中存儲有標簽標識符、密鑰等秘密信息，只有當服務器(通過閱讀器)成功認證標簽后，用戶才能從系統數據庫中檢索到該標簽及其附著物品的相關信息。因此，在協議層面上，RFID應用需要標簽認證協議作為支撐。

基于RFID的應用(尤其是供應鏈管理)，標簽會從制造商轉移到標簽發行者，再由發行者轉移到物品供應商，或再從一級物品供應商轉移到二級供應商，并最終隨商品流通至用戶。在標簽轉移過程中，其標識符和密鑰等信息(即標簽所有權，Tag ownership)將會從標簽當前擁有者的服務器轉移到新擁有者的服務器。此后，新的擁有者便能利用閱讀器成功發起對標簽的認證，并獲取標簽及其附著產品的相關信息。因此，標簽所有權轉移也需要相應協議的支撐。

圖1 RFID系統典型結構Fig. 1 Typical structure of an RFID system

但隨著RFID技術的深入應用，各種安全問題也隨之而來，如標簽及其持有者的隱私泄露問題、標簽數據的安全問題[1]等。導致這些問題的原因之一是標簽性能低，如僅支持異或運算、冗余校驗、偽隨機數產生器(為了控制標簽的商用成本)；另一個原因是RFID協議的設計缺陷和協議安全模型的缺乏。考慮到對安全要求較高的應用，如各類金融卡、電子護照/駕照、重要門禁等，低性能標簽已不能滿足此類應用要求。因此，支持公鑰加密、尤其是橢圓曲線加密(Elliptic Curve Cryptography, ECC)的標簽應運而生[2-7]。

1 相關工作

文獻[8]提出了第一個基于ECC的RFID標簽認證協議，但該協議對標簽的身份標識符沒有采取保護措施，因此標簽不具有匿名性，存在隱私泄露問題；文獻[9]提出了一個閱讀器-標簽雙向認證協議，但文獻[10]中指出該協議不具備標簽隱私保護，并易受標簽假冒攻擊和服務器假冒攻擊；基于文獻[9]的工作，文獻[11]提出了一個改進的認證協議，但文獻[12]中指出該協議不具有標簽的前向隱私保護，并引入Hash函數改進了該協議；文獻[13]提出了基于ECC的雙向認證協議，并聲稱該協議達到了標簽的強隱私保護，但文獻[14]的分析表明，在主動攻擊的情況下，該協議并不具有標簽隱私保護，同時該文獻也給出了一個改進版的協議；文獻[15]提出了一個基于ECC的認證協議，但是該協議一次執行，標簽計算開銷大(需要計算5個橢圓曲線點乘)，并易受密鑰泄露攻擊[16]；文獻[17]基于ECC和Hash函數，設計了一個雙向認證協議，但是文獻[18]中指出該協議容易遭受拒絕服務攻擊。

對于標簽所有權轉移，通常情況下:1)標簽(Ti)的當前擁有者(OC)為防止新的擁有者(ON)分析Ti在所有權轉移之前的歷史行為，會發起與Ti的認證，并改變標簽中的密鑰(甚至標識符)等所有權信息；2)OC將更新后的標簽所有權信息發送給ON；3)為防止OC發起對Ti的后續認證及分析其后續行為，ON會發起一次與Ti的認證，并更新Ti中的密鑰(甚至標簽符)等信息以完成標簽所有權轉移。

文獻[19]給出了一個具有標簽身份驗證、雙向認證和所有權轉移的方案，該方案由標簽初始化、雙向認證子協議、標簽發行者驗證子協議及標簽所有權轉移子協議構成；但該方案易受標簽以前持有者發起的隱私攻擊。文獻[20]也提出了一個基于公鑰加密的標簽所有權轉移方案，但所有權轉移過程需要一個可信第三者參與。雖然文獻[19-20]中的方案都支持標簽認證和所有權轉移功能，但方案較復雜；而目前大部分的認證協議僅具有標簽認證功能。因此，為簡化協議設計及方便RFID應用，設計安全的、并具備標簽所有權轉移功能的認證協議顯得很有必要。

基于上述工作，針對支持橢圓曲線加密的標簽，本文提出了一個閱讀器與標簽的雙向認證協議。該協議具備：1)支持標簽所有權轉移；2)閱讀器常量時間識別標簽；3)閱讀器與標簽的雙向認證；4)標簽隱私保護；5)滿足其他安全要求；6)標簽計算開銷和協議通信開銷小。此外還給出了該協議的簡化版，該簡化版協議僅實現閱讀器對標簽的單向認證，以減小協議開銷，但不支持標簽所有權轉移。

2 預備知識

2.1 橢圓曲線加密

文獻[21-22]提出了橢圓曲線加密體制：素域GF(q)上的橢圓曲線E(a,b)是對于固定的a和b，滿足形如方程y2=x3+ax+b(modq)(4a3+27b2≠0 (modq))的所有點，外加一個無窮遠點O的集合。橢圓曲線上的加法運算法則[23]包括：

1)加法單位元為O。

2)若P、Q為互逆點,則P+Q=O。

3)若P(xP,yP)與Q(xQ,yQ)不為互逆點,則P+Q=R(xR,yR)，其中：xR=λ2-xP-xQ,yR=λ(xP-xR)-yP，λ=(yQ-yP)/(xQ-xP)。

5)標量乘法：mP=P+P+…+P(共m個點作加法運算)。此外，加法運算還滿足交換律和結合律。

2.2 計算性Diffie-Hellman 問題

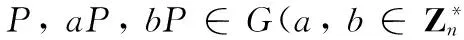
2.3 單向Hash函數

單向Hash函數h(·)是能將任意長度的輸入串/消息X映射到一個固定長度串Y的函數，其輸出串Y稱為X的Hash值，該函數具有如下性質[24]：1)X為任意長度；2)Y長度固定；3)給定算法h(·)和X，容易計算得到Y；4)給定算法h(·)，要找到兩個不同的輸入串x1≠x2，使得h(x1)=h(x2)是計算上不可行的。

如果Hash函數h(·):X→Y是安全的Hash函數，那么下面三個問題是難解的：1)原像問題，即已知y∈Y，求x∈X，使得h(x)=y是困難的；2)第二原像問題，即已知x∈X，求x′∈X，使得x≠x′且h(x)=h(x′)成立；3)碰撞問題，即找到x,x′∈X，使得x≠x′且h(x)=h(x′)成立。

3 提出的RFID認證協議

針對支持ECC的RFID標簽，本章提出一個閱讀器與標簽的雙向認證協議。下面給出本文所使用的符號和協議的流程描述，并給出相應解釋。

3.1 符號

為方便描述，表1列出了后續章節所使用的相關符號。

表1 符號說明Tab. 1 Notations

3.2 協議描述

由于閱讀器和后臺服務器支持復雜的密碼運算，具有較強的運算能力和存儲能力，雙方在通信前會建立安全信道。因此，為簡單起見又不失一般性，假定閱讀器集成后臺數據庫。圖2給出了本文所提出協議(簡稱PI)的流程描述。

R(toi,ti,y,Y=yP,P) Ti(ti,Y,P)r1∈RZ*n,M1=r1P M1→ r2∈RZ*nM2=r2Pk=r2(M1+Y)m3=ti+h(M1,M2,k)m4=h(M2,k,ti)M2,m3,m4←k=(r1+y)M2t'i=m3-h(M1,M2,k)m'4=h(M2,k,ti)m″4=h(M2,k,toi)searchest'iindatabaseif(ti=t'iandm4=m'4)or(toi=t'iandm4=m″4) returnstagsinformationandcomputes: m5=h(M1,M2,k,t'i) toi=t'i ti=[h(t'i,k)]lTelsereturnsm5∈R{0,1}lHm5→if(m5=h(M1,M2,k,ti))computesti=[h(ti,k)]LTelseauthenticationfailed

圖2 本文協議PI的流程

Fig. 2 Process of the proposed protocol (abbreviated as PI)

1)閱讀器R產生一個隨機數r1，并計算M1=r1P，然后發送M1至標簽Ti。

2)當收到M1，標簽Ti產生隨機數r2，并計算M2=r2P,k=r2(M1+Y),m3=ti+h(M1,M2,k)和m4=h(M2,k,ti)，然后發送M2,m3和m4至R。

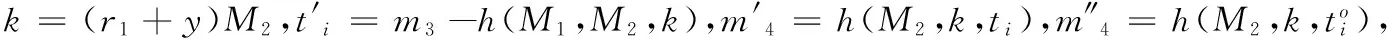
4)收到m5后，Ti檢查m5=h(M1,M2,k,ti)是否成立，如果成立，Ti計算并更新標識符為ti=[h(ti,k)]lT；否則，Ti認證R失敗，不更新身份標識符。

4 協議分析

本章將從協議層面對協議支持標簽所有權轉移、閱讀器識別標簽時間、閱讀器-標簽雙向認證、標簽的隱私保護及協議的其他安全屬性要求進行證明和分析。

4.1 支持標簽所有權轉移

若標簽持有者R1欲將標簽Ti的所有權轉移給新的持有者R2，只需：

1)R1向Ti寫入R2的公鑰及R2使用的群的生成元。

2)R1將Ti的標識符及其相關信息通過安全信道發送至R2。

3)R2與Ti執行一次協議(以便進行相互認證并更新標識符)，即可完成該標簽的所有權轉移。

因此，協議PI具有閱讀器-標簽相互認證與標簽所有權轉移功能，且所有權轉移過程簡單、高效，不需要另行設計標簽所有權轉移協議，也不需要可信第三方參與。

4.2 標簽常量時間識別

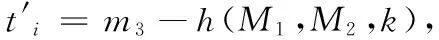
4.3 閱讀器-標簽雙向認證

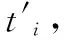
另一方面，在收到R發來的消息m5后，Ti驗證m5是否等于h(M1,M2,k,ti)。由于m5是由R所存儲的標簽標識符參與計算得到，因此，若驗證成功，則實現了標簽對閱讀器的認證。

4.4 標簽隱私保護

4.4.1 標簽匿名性

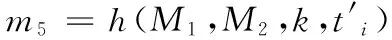
4.4.2 標簽前向隱私安全

在RFID應用系統中，由于閱讀器與標簽的通信信道為無線信道，敵手可竊聽、攔截、篡改、偽造通信雙方的交互信息，甚至破解標簽從而獲得標簽的內部數據(包括身份標識符、標簽密鑰等所有信息)。如果一個概率多項式時間敵手A，在破解標簽之后，仍無法識別該標簽與閱讀器的后續交互信息，則稱標簽是前向隱私安全的(協議具備標簽前向隱私保護)；如果A在破解標簽之后，無法識別該標簽未被破解之前的與閱讀器的交互信息，則稱標簽是后向隱私安全的(協議具備標簽后向隱私保護)。根據文獻[25-27]，給出如下基于挑戰者游戲的標簽前向和后向隱私安全證明。

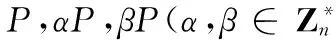
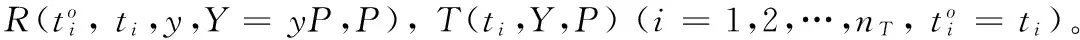
2)第二階段：因挑戰者C知道所有標簽的身份標識符和閱讀器的私鑰，C可以為A提供真實的攻擊環境，即當A竊聽、攔截、篡改或偽造任意標簽與閱讀器的通信消息，甚至破解標簽以獲取其內部信息時，C按真實場景進行模擬并返回相應的結果給A。

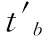
證明 在挑戰之前，由于T0和T1已被A攻破，即A已知兩者的身份標識符。若A贏得游戲，則他必定通過下面三種方式確定哪一個標簽被選中。

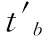
3)根據第三階段挑戰者返回的協議執行腳本：M1=αP,M2=βP,m3=tb+h(M1,M2,k)m4=h(M2,k,tb)和m5=h(M1,M2,k,tb)來推導T0還是T1被選中，即找到協議執行腳本與被選中標簽的關聯，那么A可以：

①通過猜測隨機數α或β，從而計算出臨時密鑰k，并進一步計算出tb=m3-h(M1,M2,k)。但是A猜中正確的隨機數α或β的概率為1/lN，即這種方式正確推測出b′的概率為1/lN。

由于1)、2)和①方式猜測正確的b′的概率可忽略不計，若A以不可忽略的概率給出正確的b′(即攻破協議的標簽前向隱私保護)，那么他必然以不可忽略的概率正確地計算出了臨時密鑰k。因此，挑戰者C就能以不可忽略的概率計算出k′=k-yM2，也即：由M1=αP和M2=βP計算出k′=αβP，從而解決橢圓曲線上的CDHP問題。

綜合1)、2)和3)，協議PI具備標簽前向隱私保護。

4.4.3 標簽后向隱私安全

證明 由于4.4.2節已證明：即使A在知道T0和T1身份標識符的情況下，仍無法以不可忽略的概率給出正確的b′，因此，在未知標簽身份標識符的條件下，A攻破標簽后向隱私安全的概率是可忽略的。

4.5 協議其他安全屬性分析

4.5.1 抵抗標簽假冒攻擊

當閱讀器R發送隨機數給標簽Ti后，Ti回送閱讀器M2=r2P,m3=ti+h(M1,M2,k)和m4=h(M2,k,ti)，由于m3和m4是由標識符ti參與計算得來，在未知ti的情況下，攻擊者不能偽造m3和m4，除非以概率1/lT猜中ti。

4.5.2 抵抗閱讀器假冒攻擊

攻擊者不能偽造閱讀器R發送的第三輪消息m5=h(M1,M2,k,ti)，以達到假冒R從而通過標簽的驗證。因為臨時密鑰k和標簽標識符ti參與了對m5的計算。在未知ti和閱讀器私鑰y的情況下，敵手不能偽造m5，除非以概率1/lT猜中正確的ti和y。

4.5.3 抵抗中間人攻擊

由于閱讀器與標簽共享的ti參與了第二輪消息M2,m3,m4和第三輪消息m5的計算，且閱讀器的私鑰y也參與了對m5的計算，因此，該協議抵抗中間人攻擊。

4.5.4 抵抗消息重放攻擊

協議使用的臨時密鑰k由閱讀器與標簽臨時產生的隨機數r1和r2計算得到，協議的第二輪消息和第三輪消息均由k參與計算得到。因此，該協議抵抗消息重放攻擊。

4.5.5 抵抗去同步攻擊

4.5.6 抵抗拒絕服務攻擊

目前，絕大部分RFID認證協議都由閱讀器首先發起協議會話，該類協議不可避免地存在攻擊者持續發動第一輪消息以阻止標簽響應合法閱讀器發起的認證會話，或阻塞第二輪消息以阻止閱讀器接收合法標簽的響應信號。如果應用中頻繁出現認證不成功的情況，可通過外部的物理設備(如無線信號探測儀)對此類攻擊進行監測。

另外，為使閱讀器認證標簽頻繁失敗而不再響應標簽信息，攻擊者可通過阻塞PI的第三輪消息進行去同步攻擊。但PI實現了閱讀器與標簽的再同步功能，可以抵抗此類攻擊。

5 協議性能對比

由于標簽屬于計算受限設備，本章從標簽的計算開銷和協議的通信開銷兩個方面，對所提出協議PI與近期其他基于標簽支持ECC的協議[9,11-15, 17]進行分析對比。

用Tmm表示一次模乘操作所需時間，Tea表示一次橢圓曲線加法運算所需時間，Tem表示一次橢圓曲線標量乘法運算所需時間，Tha表示一次Hash運算所需時間。根據文獻[28]的工作，1 Tha≈0.36 Tmm,1 Tea≈5 Tmm，1 Tem≈1 200 Tmm。為公平起見，將所有的運算時間統一為Tmm。

為保證協議安全，選擇基于有限域GF(2160)的橢圓曲線，則橢圓曲線上一個點P的二進制位數|P|=40 Byte，選擇輸出長度為10 Byte的Hash函數[29]。經分析，表2給出了相關協議的標簽計算開銷和協議通信開銷。

表2 協議性能比較Tab.2 Comparisons of performance of related protocols

從表2看出，在標簽計算開銷上，所提出的協議PI與文獻[11-12]中的協議性能最優，而文獻[15]協議的計算開銷最大。其主要原因在于文獻[15]中的協議執行一次，標簽要執行5次標量乘法運算；而PI和文獻[11-12]中的協議只需執行2次標量乘法運算，因而計算開銷小。

在協議通信開銷上，PI與文獻[12]中的協議性能最優，而文獻[17]中協議的通信開銷最大。其主要原因在于文獻[17]中的協議由三個子協議構成，執行一次標簽認證，三個子協議均要執行一次，所以通信開銷較大；而協議PI只需執行一次就可完成雙向認證，因而通信開銷小。

雖然文獻[12]中提出的協議與PI在標簽計算開銷與協議通信開銷方面取得最優效果，但PI具有標簽所有權轉移功能。另外，文獻[10，12，14]分別對[9，11，13]提出的協議進行了分析，指出其均不具有標簽隱私保護。因此，從標簽計算開銷、協議通信開銷、標簽隱私保護和支持標簽所有權轉移方面綜合評估，本文所提出的協議PI優于對比協議。

6 協議簡化版

考慮到RFID系統應用于比較安全的場合，比如應用環境安裝有屏蔽外界電磁干擾設備或無線信號探測設備、有警察或安保把守等，為減少標簽計算開銷和協議通信開銷并提高協議性能，所提出的協議也可以簡化為閱讀器對標簽的單向認證協議(簡記為PII)，如圖2所示。

R(ti,y,Y=yP,P) T(ti,Y,P)r1∈RZ*n,M1=r1PM1→r2∈RZ*nM2=r2Pk=r2(M1+Y)m3=ti+h(M1,M2,k)m4=h(M2,k,ti)M2,m3,m4←k=(r1+y)M2t'i=m3-h(M1,M2,k)m'4=h(M2,k,ti)searchest'iindatabaseif(ti=t'iandm4=m'4)returnstagsinformation

圖2 簡化版協議PII

Fig. 2 Reduced version of PI (abbreviated as PII)

PII協議沒有第三輪消息及對其驗證步驟，執行一次協議，標簽計算開銷為2次橢圓曲線標量乘法運算和2次Hash運算，協議通信開銷100 Byte。

簡化版協議實現了閱讀器對標簽的單向認證，但不支持標簽所有權轉移。該協議具備標簽匿名性、標簽前向隱私和后向隱私保護、抵抗標簽假冒攻擊、抵抗中間人攻擊、抵抗消息重放和去同步攻擊；但由于缺乏標簽對閱讀器的認證，為防止閱讀器假冒攻擊，PII協議適用于相對安全的應用環境。

7 結語

針對支持ECC的RFID標簽，為滿足開放環境下對標簽隱私保護和數據安全要求較高的RFID應用，設計了一個閱讀器與標簽的雙向認證協議，該協議支持標簽所有權轉移，具有對標簽的常量時間識別。本文證明了該協議具備標簽前向隱私和后向隱私保護，并分析了該協議的其他安全屬性，如抵抗閱讀器/標簽假冒攻擊、抵抗中間人及消息重放攻擊、抵抗去同步攻擊和拒絕服務攻擊。經過對近年來提出的類似協議在標簽計算開銷、協議通信開銷、標簽隱私保護以及能否支持標簽所有權轉移等方面的比較，結果表明本文提出的協議PI具備最優的綜合性能。而且為了適應比較安全的應用場景，本文也給出了簡化版的單向認證協議PII，但該協議不具備標簽所有權轉移。

目前，RFID認證協議的安全屬性證明大都采用啟發式分析，還沒有較好的形式化證明方法。因此，探索RFID協議安全屬性的形式化證明方法，具有重要意義。另外，協議的應用測試也是我們考慮的后續工作。

References)

[1] The Commission of the European Communities. Commission recommendation of 12 May 2009 on the implementation of privacy and data protection principles in applications supported by radio-frequency identification [EB/OL]. (2009- 05- 12) [2016- 12- 05]. https://ec.europa.eu/digital-singlemarket/en/news/commission-recommendation-12-may-2009-implementation-privacyand-data-protection-prin-ciples/.

[2] BATINA L, GUAJARDO J, KERINS T, et al. Public-key cryptography for RFID-tags [C]// PerCom Workshops ’07: Proceedings of the Fifth Annual IEEE International Conference on Pervasive Computing and Communications Workshops. Piscataway, NJ: IEEE, 2007: 217-222.

[3] FURBASS F, WOLKERSTORFER J. ECC processor with low die size for RFID applications [C]// ISCAS 2007: Proceedings of the 2007 IEEE International Symposium on Circuits and Systems. Piscataway, NJ: IEEE, 2007: 1835-1838.

[4] HEIN D, WOLKERSTORFER J, FELBER N. ECC is ready for RFID - a proof in silicon [C]// SAC 2008: Proceedings of the 2008 International Workshop on Selected Areas in Cryptography, LNCS 5381. Berlin: Springer-Verlag, 2008: 401-413.

[5] LEE Y K, SAKIYAMA K, BATINA L, et al. Elliptic-curve-based security processor for RFID [J]. IEEE Transactions on Computers, 2008, 57(11): 1514-1527.

[6] LIU D, LIU Z, YONG Z, et al. Design and implementation of an ECC-based digital baseband controller for RFID tag chip [J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4365-4373.

[7] PENDL C, PELNAR M, HUTTER M. Elliptic curve cryptography on the WISP UHF RFID tag [C]// RFIDSec 2011: Proceedings of the 2011 International Workshop on Radio Frequency Identification: Security and Privacy Issues, LNCS 7055. Berlin: Springer-Verlag, 2011: 32-47.

[8] TUYLS P, BATINA L. RFID-tags for anti-counterfeiting [C]// CT-RSA’06: Proceedings of the 2006 Cryptographers’ Track at the RSA Conference on Topics in Cryptology, LNCS 3860. Berlin: Springer-Verlag, 2006: 115-131.

[9] CHOU J-S. An efficient mutual authentication RFID scheme based on elliptic curve cryptography [J]. Journal of Supercomputing, 2014, 70(1): 75-94.

[10] FARASH M S. Cryptanalysis and improvement of an efficient mutual authentication RFID scheme based on elliptic curve cryptography [J]. Journal of Supercomputing, 2014, 70(2): 987-1001.

[11] ZHANG Z, QI Q. An efficient RFID authentication protocol to enhance patient medication safety using elliptic curve cryptography [J]. Journal of Medical Systems, 2014, 38(5): 47.

[12] FARASH M S, NAWAZ O, MAHMOOD K, et al. A provably secure RFID authentication protocol based on elliptic curve for healthcare environments [J]. Journal of Medical Systems, 2016, 40(7): 165.

[13] HE D, KUMAR N, CHILAMKURTI N, et al. Lightweight ECC based RFID authentication integrated with an ID verifier transfer protocol [J]. Journal of Medical Systems, 2014, 38(10): 116.

[14] LEE C-I, CHIEN H-Y. An elliptic curve cryptography-based RFID authentication securing E-health system [J]. International Journal of Distributed Sensor Networks, 2015, 2015: Article No. 251.

[15] LIAO Y-P, HSIAO C-M. A secure ECC-based RFID authentication scheme integrated with ID-verifier transfer protocol [J]. Ad Hoc Networks, 2014, 18: 133-146.

[16] ZHAO Z. A secure RFID authentication protocol for healthcare environments using elliptic curve cryptosystem [J]. Journal of Medical Systems, 2014, 38(5): 46.

[17] MOOSAVI S R, NIGUSSIE E, VIRTANEN S, et al. An elliptic curve-based mutual authentication scheme for RFID implant systems [J]. Procedia Computer Science, 2014, 32: 198-206.

[18] KHATWANI C, ROY S. Security analysis of ECC based authentication protocols [C]// CICN 2015: Proceedings of the 2015 International Conference on Computational Intelligence and Communication Networks. Piscataway, NJ: IEEE, 2015: 1167-1172.

[19] ELKHIYAOUI K, BLASS E-O, MOLVA R. ROTIV: RFID ownership transfer with issuer verification [C]// RFIDSec 2011: Proceedings of the 2011 International Workshop on Radio Frequency Identification: Security and Privacy Issues, LNCS 7055. Berlin: Springer-Verlag, 2011: 163-182.

[20] XIN W, GUAN Z, YANG T, et al. An efficient privacy-preserving RFID ownership transfer protocol [C]// APWeb 2013: Proceedings of the 2013 Asia-Pacific Web Conference on Web Technologies and Applications, LNCS 7808. Berlin: Springer-Verlag, 2013: 538-549.

[21] KOBLITZ N. Elliptic curve cryptosystems [J]. Mathematics of Computation, 1987, 48(177): 203-209.

[22] MILLER V S. Use of elliptic curves in cryptography [C]// CRYPTO 1985: Proceedings of the 1985 Conference on the Theory and Application of Cryptographic Techniques, LNCS 218. Berlin: Springer-Verlag, 1985: 417-426.

[23] 鄧元慶,龔晶,石會.密碼學簡明教程[M].北京:清華大學出版社,2011:125-129. (DENG Y Q, GONG J, SHI H. Concise Course in Cryptography [M]. Beijing: Tsinghua University Press, 2011: 125-129.

[24] MERKLE R C. One way Hash functions and DES [C]// CRYPTO 1989: Proceedings of the 1989 Conference on the Theory and Application of Cryptology, LNCS 435. Berlin: Springer-Verlag, 1989: 428-446.

[25] 馬昌社.前向隱私安全的低成本RFID認證協議[J].計算機學報,2011,34(8):1387-1398. (MA C S. Low cost RFID authentication protocol with forward privacy [J]. Chinese Journal of Computers, 2011, 34(8): 1387-1398.)

[26] JUELS A, WEIS S A. Defining strong privacy for RFID [C]// PerCom Workshops ’07: Proceedings of the 2007 IEEE International Conference on Pervasive Computing and Communications Workshops. Piscataway, NJ: IEEE, 2007: 342-347.

[27] OUAFI K, PHAN R C-W. Traceable privacy of recent provably-secure RFID protocols [C]// ACNS 2008: Proceedings of the 2008 International Conference on Applied Cryptography and Network Security, LNCS 5037. Berlin: Springer-Verlag, 2008: 479-489.

[28] CHATTERJEE S, DAS A K, SING J K. An enhanced access control scheme in wireless sensor networks [J]. Ad Hoc & Sensor Wireless Networks, 2014, 21(1): 121-149.

[29] AUMASSON J-P, HENZEN L, MEIER W, et al. QUARK: a lightweight hash [C]// CHES 2010: Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, LNCS 6225. Berlin: Springer-Verlag, 2010: 313-339.

This work is partially supported by the National Natural Science Foundation of China (61370203), the Nature Science Foundation of Sichuan Province Education Department (13ZB0127).

YANGXingchun, born in 1975, Ph. D. candidate, associate professor. His research interests include information security, cryptography, wireless network security.

XUChunxiang, born in 1965, Ph. D., professor. Her research interests include information security, cloud computing, cryptography.

LIChaorong, born in 1976, Ph. D., associate professor. His research interests include pattern recognition, information security.

ECC-basedRFIDauthenticationprotocolenablingtagownershiptransfer

YANG Xingchun1,2*, XU Chunxiang1, LI Chaorong3

(1.SchoolofComputerScienceandEngineering,UniversityofElectronicScienceandTechnologyofChina,ChengduSichuan611731,China；2.DepartmentofComputerScienceandTechnology,SichuanPoliceCollege,LuzhouSichuan646000,China；3.SchoolofComputerandInformationEngineering,YibinUniversity,YibinSichuan644000,China)

To solve privacy leakage and other security problems in Radio-Frequency Identification (RFID) tag authentication and tag ownership transfer, and to simplify the design of tag ownership transfer protocol, an RFID authentication protocol enabling tag ownership transfer was proposed for those tags that support Elliptic Curve Cryptography (ECC). The structure of the protocol is similar to the structure of the Diffie-Hellman logarithm, and tag privacy of the protocol is based on complexity to solve the computational Diffie-Hellman problem. Analysis of tag privacy and other security properties of the protocol were given, and comparisons between recent ECC-based authentication protocols and the proposed protocol were also given. The results show that the proposed protocol achieves best performance, under a comprehensive evaluation of supporting tag ownership transfer, tag computation cost, communication cost and tag privacy protection. In addition, a simplified version that realizes tag authentication to reader and is suitable for secure environments was also given.

Radio-Frequency Identification (FRID); authentication protocol; tag; ownership transfer; Elliptic Curve Cryptography (ECC)

TP309.2

A

2017- 02- 28;

2017- 04- 18。

國家自然科學基金資助項目(61370203)；四川省教育廳資助項目(13ZB0127)。

楊興春(1975—)，男，四川南充人，副教授，博士研究生，CCF會員，主要研究方向：信息安全、密碼學、無線網絡安全； 許春香(1965—)，女，湖南寧鄉人，教授，博士生導師，博士，主要研究方向：信息安全、云計算、密碼學； 李朝榮(1976—)，男，四川宜賓人，副教授，博士，主要研究方向：模式識別、信息安全。

1001- 9081(2017)08- 2275- 06

10.11772/j.issn.1001- 9081.2017.08.2275