基于新型二維核函數動態X參數的功放建模

南敬昌，崔洪艷

(遼寧工程技術大學 電子與信息工程學院，遼寧 葫蘆島 125105)

(*通信作者電子郵箱cuihongyan8023@163.com)

基于新型二維核函數動態X參數的功放建模

南敬昌，崔洪艷*

(遼寧工程技術大學 電子與信息工程學院，遼寧 葫蘆島 125105)

(*通信作者電子郵箱cuihongyan8023@163.com)

為了更準確地描述帶有記憶效應的射頻(RF)功放特性，基于傳統的動態X參數模型，結合功放長期記憶效應以及短期記憶效應機理，提出一種新型動態X參數功放建模方法。新模型保留X參數模型的靜態核函數，利用雙記憶路徑模型提取出表征記憶效應的非線性函數，替換動態核函數。采用輸出信號為幅度與頻率雙變量的新型反饋(FB)結構，引入時變頻率變量而簡化動態核函數為二維核函數。使用MW6S010N設計功放并建模，由仿真可知，新模型在單音大信號及碼分多址(CDMA)信號激勵下，均能正確表征功放特性，歸一化均方誤差(NMSE)較靜態X參數模型、傳統動態X參數模型以及前饋(FF)結構X參數模型分別減少8.0 dB、6.3 dB、2.5 dB。結果表明該模型能夠更加準確擬合帶有非線性記憶效應功率放大器的特性。

二維核函數；動態X參數；反饋結構；記憶效應；功率放大器；行為模型

0 引言

隨著無線通信系統的不斷升級，在面對更大帶寬、更高峰均比的調制信號情況下，射頻功放固有的非線性和記憶效應嚴重影響通信質量。射頻功放在不同的寬帶信號下所呈現的非線性特性并不相同，無記憶功放模型在這樣情況下難以滿足設計要求，導致器件建模變得更加困難和復雜。在對射頻微波電路的非線性行為模型研究中，急待攻克的難題主要是如何對具有記憶效應的非線性功放進行精確的動態建模，并方便地應用于系統級仿真，來獲得功放更優的性能。為了評估以及降低功放的記憶非線性效應對通信系統造成的影響，功放器件的非線性建模方法成為當前無線通信領域中的一個重要課題。

功放行為模型建模是利用功放輸入及輸出數據建立描述功放行為特性的數學模型技術[1]。目前表征帶有記憶效應的功放行為模型主要有Volterra級數模型、神經網絡模型、動態X參數模型。基于Volterra理論及其多項式的功放模型被認為是最能夠準確描述功放特性的模型[2]，然而這種近似隨著功放非線性增強以及記憶效應加深，使Volterra級數模型的參數辨識變得非常復雜，限制了其對強記憶及強非線性功放的建模。神經網絡模型擁有很強的學習能力和逼近能力，但模型泛化能力不強，難以由硬件實現。安捷倫提出了基于測量的X參數模型理論及基于非線性矢量網絡分析儀(Nonlinear Vector Network Analyzer，NVNA)平臺的測試系統[3-4]，作為一種集測量、建模和設計非線性器件的新方法，受到了廣泛關注。Jan Verspecht博士在文獻[5]中首次提出動態X參數模型，引入了表征長期記憶效應的三維核函數，而三維核函數的提取及驗證都極為困難；而后該團隊在文獻[6-7]針對該模型將記憶效應核函數簡化成二維的核函數，一定程度上簡化了模型及參數辨識過程，但是模型精度不高。文獻[8]提出基于反饋(FeedBack，FB)結構的動態X參數模型，提出一種表征功放記憶效應的新方法，但模型僅考慮功放的長期記憶效應，參數辨識困難且普適性差。文獻[9]中提出利用前饋(FeedForward, FF)結構構建動態X參數模型，同時考慮兩種記憶效應在建模中的影響，在模型的精度和提取速度上有了一定提高，但是僅僅將兩種記憶效應簡單疊加，不符合功放記憶效應的產生機制，模型泛化能力不強，模型的精度以及應用范圍受到限制。

基于以上的研究，本文提出一種利用新型FB結構的動態X參數模型建模方法。該方法將模型分為靜態部分與動態部分。靜態部分的核函數為多諧波失真(Poly Harmonic Distortion，PHD)模型，以保證模型對強非線性的正確表征；考慮短期記憶(Short-Term Memory，STM)效應以及長期記憶(Long-Term Memory，LTM)效應相互作用關系，利用雙記憶路徑模型提取表征記憶效應的非線性函數，替換動態核函數，以提高模型精度；采用將輸出信號分為雙變量的新型FB結構，引入時變頻率變量將三維動態核函數簡化為二維核函數，以簡化動態核函數的提取過程，降低模型的復雜度。經過實驗驗證，新的動態X參數模型比靜態X參數模型、傳統動態X參數模型以及FF結構的動態X參數模型精度更高，仿真速度與已有兩種動態模型相當。

1 模型分析

1.1 靜態X參數模型

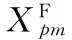
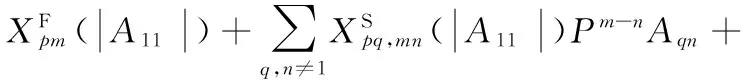
(1)

1.2 傳統動態X參數模型

按照產生信號失真的強弱，將記憶效應分為STM效應和LTM效應[11]。STM效應主要由匹配電路、晶體管內的運轉時間引起；LTM效應主要由偏置電路、自動增益控制電路、晶體管自熱以及陷阱效應引起。這種雙記憶效應相互作用的關系如圖1所示。

傳統動態X參數模型引入了功放LTM效應對功放模型的影響，輸出諧波表達式如式(2)所示。它是由當前輸入|A(t)|、過去輸入|A(t-τ)|及時間跨度τ構成的具有三維核函數的動態X參數模型。

B(t)=Xm(|A(t)|)·Φ(t)+

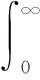
(2)

整個模型是由靜態非線性部分及動態非線性部分疊加得到，Xm(·)表征靜態核函數，G(·)表征動態核函數，Φ(t)=exp[jφ(A(t))]代表輸入信號的相位函數。

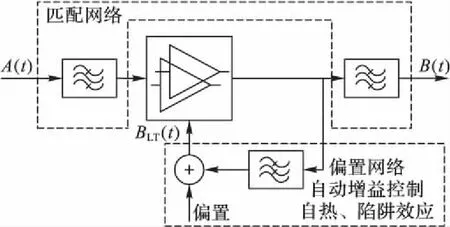
圖1 功放雙記憶路徑相互作用原理Fig. 1 Amplifier two-memory-path interaction principle

1.3 FB結構模型

假設功放的輸入信號是一個帶通調制信號，如下所示：

x(t)=Re(|A(t)|)·ejωt)

(3)

其中：|A(t)|為輸入調制信號的包絡，ω為輸入信號的載波頻率。對于功放模型，需要確認包絡輸入|A(t)|以及輸出包絡|B(t)|，則基于FB拓撲結構[12]的模型如圖2所示。

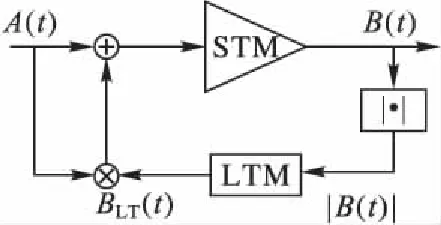
圖2 FB模型的拓撲Fig. 2 Topology of FB model

根據功放的電路結構建立雙記憶路徑模型。模型結構中STM路徑的作用是捕獲功放主動態，擔當著放大以及濾波的作用。當一個時變包絡信號通過這條路徑時，STM路徑的短期非線性作用將會產生一個低頻信號反饋到LTM路徑中，LTM路徑本身是動態非線性，進而影響STM路徑。

根據這樣的結構，得到雙記憶路徑模型表達式如下：

B(t)=α(|A(t)|,t)·(1+BLT(t))·|A(t)|

(4)

BLT(t)=β(|A(t)|,t)·|B(t)|

(5)

其中：α(|A(t)|,t)代表功放的增益，β(|A(t)|,t)代表反饋系數。當單獨考慮STM及LTM路徑的效應時，用以下非線性積分[13]表示：

(6)

(7)

則輸出包絡信號可以表示為：

[1+BLT(t-τ)]·A(t-τ)dτ

(8)

2 二維核函數模型

傳統功放模型的核函數只是關于當前及過去輸入信號幅度的函數，為了提高模型精度，在核函數中引入了新的變量——時變頻率，同時將X參數的動態核函數簡化成為只與輸入信號包絡幅度和時變頻率相關的二維核函數。在上述的傳統FB結構中，在求解核函數時需要求解一個不對稱方程，難以得到精確的核函數，因此結合時變頻率變量，改進FB模型的拓撲結構，將模型輸出包絡信號分解為幅度與頻率的二維變量，分別提取對應的LTM效應核函數，新的拓撲結構如圖3所示。

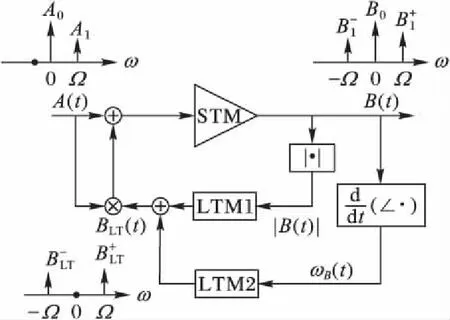
圖3 改進的FB模型拓撲結構Fig. 3 Topology structure of the improved FB model

考慮信號變化節點，改進的FB結構模型表達式如下所示:

[1+BLT(t-τ)]·A(t-τ)dτ

(9)

式中：

(10)

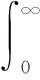
(11)

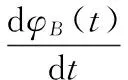
(12)

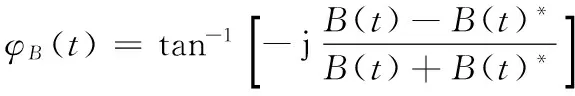
(13)

為了簡化核函數，引入時變頻率核替換式(9)中的非線性脈沖響應函數，如式(14)～(16)所示：

(14)

(15)

(16)

新的動態X參數模型如式(17)，在其靜態部分采用PHD模型表征功放強非線性的特性，動態部分采用提出的新動態核函數模型表征功放STM效應和LTM效應的特性。

(17)

其中：

G(|A(t)|,Ω)=HST(|A(t)|,Ω)·

(1+HLT(|A(t)|),Ω)

(18)

HLT(|A(t)|,Ω)=HLT1(|A(t)|,Ω)+

HLT2(|A(t)|,Ω)

(19)

3 提取模型動態核函數

3.1 STM核函數

根據記憶效應的原理，當輸入信號的幅度不變時，在任何時間輸出信號包絡的變化都是源于STM效應的影響。因此，STM核函數容易通過包絡恒定的調制信號進行測量，這時LTM路徑效應為零。假設功放輸入信號一個幅度固定為常數的單音連續信號：

A(t)=Re(A0·ej(ω+Ω)t)

(20)

這時輸入信號的包絡可以由式(21)表示：

(21)

則輸出信號的包絡顯然是關于輸入信號包絡幅度及頻率的函數，可以由式(22)表示：

B(t)=B0(|A0|,Ω)ejΩ t

(22)

將式(21)及式(22)代入到式(9)中，得到輸出信號：

B0(A0,Ω)ejΩ t=(1+HLT(|A0|,0))·

HST(|A0|,Ω)A0ejΩ t

(23)

整理后發現：

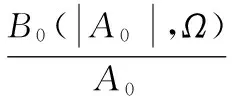
(24)

根據LTM效應的產生機理可知輸入恒定包絡的信號時，HLT(|A0|,0)應該為零，因此得到STM核函數為式(25)：

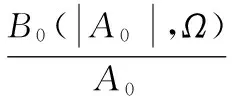
(25)

3.2 LTM核函數

使用雙音信號激發功放的LTM效應用以提取LTM核函數。輸入信號如式(26)所示，為一個恒定包絡的大信號A0與變包絡的小信號A1的疊加。

A(t)=Re(A0·ejωt+A1·ej(ω+Ω)t)

(26)

輸入信號的包絡為:

(27)

當輸入雙音信號時，輸出端得到一個三音信號，而在LTM核函數處將得到一個雙音反饋信號，如圖3所示。得到節點信號如下：

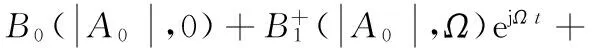
(28)

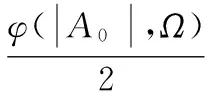
(29)

(30)

通過實驗測量可以直接獲得輸出信號B(t)和頻率ωB(t)。將輸入包絡信號代入式(9)，并考慮STM效應影響，得到輸出包絡：

(31)

(32)

(33)

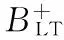
(34)

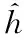
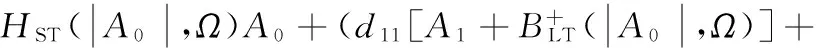
(35)

其中：

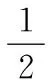
(36)

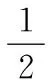
(37)

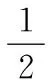
(38)

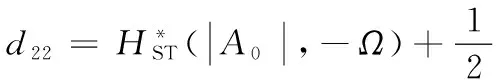
(39)

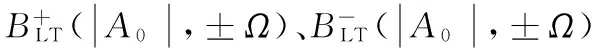
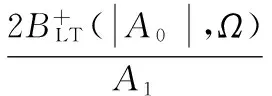
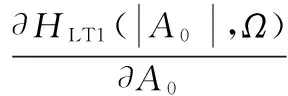
HLT2(|A0|,Ω)

(40)

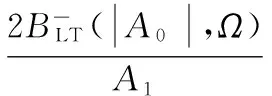
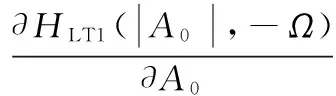
(41)

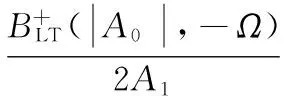
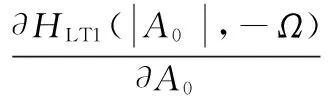
ΩM2(|A0|,-Ω)·HLT2(|A0|,-Ω)

(42)

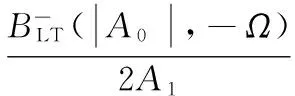
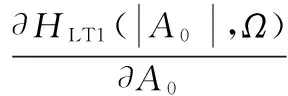
(43)

其中：

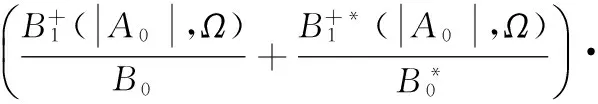
(44)

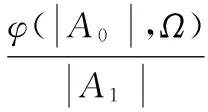
(45)

B0=B0(A0,0)

(46)

通過以上推導得到HLT1(|A0|,Ω)、HLT2(|A0|,Ω)兩個LTM核函數。由式(40)～(43)可以看出LTM效應的輸出分量分別與輸出包絡信號的幅度及時變頻率相關，故使用新結構求解動態核函數更為快捷方便，符合記憶效應對功放影響的機理。

4 模型實現和驗證

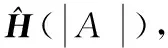
(47)

使用恩智浦公司的MW6S010N晶體管設計一款單級功放，其工作的中心頻率為850 MHz，工作帶寬為30 MHz。使用雙向負載牽引方法完成電路匹配設計，設計好的電路增益仿真如圖4所示。功放在輸入功率達到約22 dBm時進入非線性區，隨著輸入功率增大而出現增益壓縮。

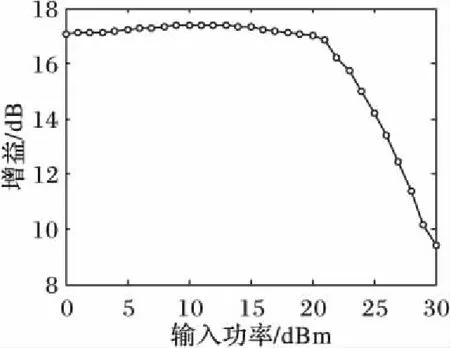
圖4 頻率為850 MHz功放增益Fig. 4 Gain of power amplifier at 850 MHz

利用ADS產生如式(20)及式(26)的大信號激勵功放，式中A0取值范圍為0～7.103 V，A1取值范圍0～1.529 V。當A0和A1均取最大值時輸入信號功率為25 dBm，如圖4所示，這時功放約有3 dB增益壓縮。在功放整個帶寬選擇30個頻點，每個頻點取20個幅度值，用以構建核函數。提取輸入輸出數據，分別提取STM及LTM核函數并在Matlab中進行建模并仿真，核函數提取結果如圖5所示。

圖5 新模型核函數Fig. 5 Kernel functions of the new model

使用單音大信號激勵功放及功放模型，測量輸出端口各次諧波幅度值，如圖6所示。隨著功放非線性增強，二次諧波及三次諧波急劇上升，新模型能夠很好地預測功放強非線性失真。

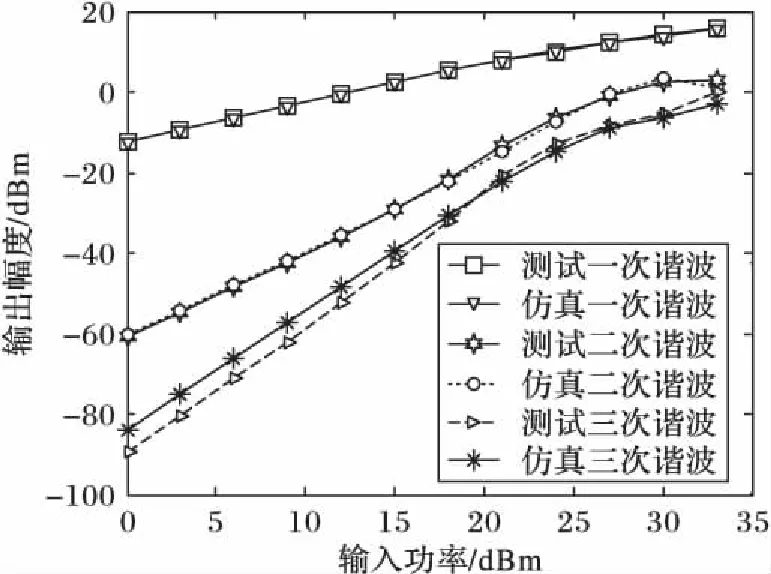
圖6 功放輸出端各次諧波Fig. 6 Power output of each harmonic

利用ADS產生帶寬為1.5 MHz的IS- 95 碼分多址(Code Division Multiple Access, CDMA)信號激勵功放模型，對功放進行鄰信道功率比(Adjacent Channel Power Ratio，ACPR)分析，可見由于記憶效應引起左、右ACRP數值不對稱，如圖7所示，新模型與測量獲得數據具有良好一致性。如式(48)及式(49)，通過對輸出信號的自相關函數R(τ)進行傅里葉變換得到功率譜密度P(f)。將新模型與四種已有的X參數模型輸出功率譜進行比較，如圖8所示，圖8(b)為局部放大圖。由圖8可知靜態模型在預測記憶效應引起的功放非線性失真時誤差較大；在三種動態X參數模型中，新模型較傳統動態X參數模型及FF結構的動態X參數模型能更精確地模擬功率放大器特性，準確預測功放的帶內失真及帶外頻譜再生。

(48)

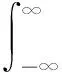
(49)

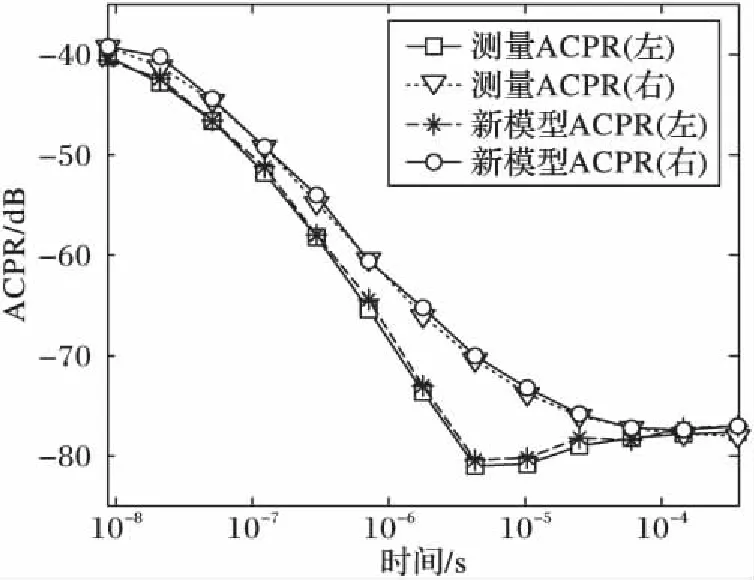
圖7 功放ACPR分析Fig. 7 ACPR analysis of power amplifier

利用歸一化均方誤差(Normalized Mean Square Error，NMSE)分析對四種模型的時域性能進行分析，并對仿真時間進行比較。NMSE可以表示為：

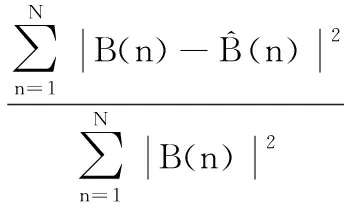
(50)

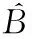
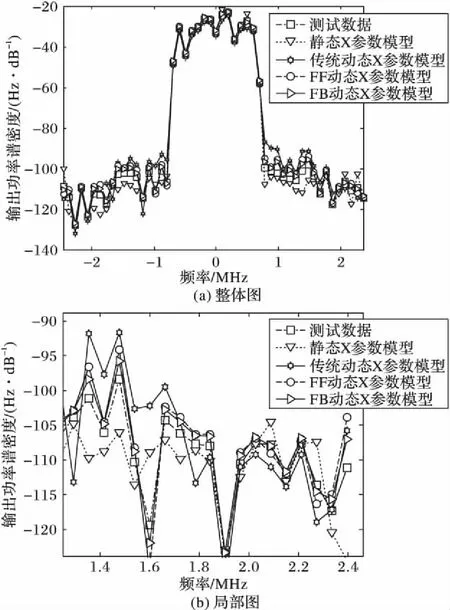
圖8 模型輸出功率譜密度Fig. 8 Power spectral density of the model output表1 模型特性比較Fig. 1 Comparison of model characteristics

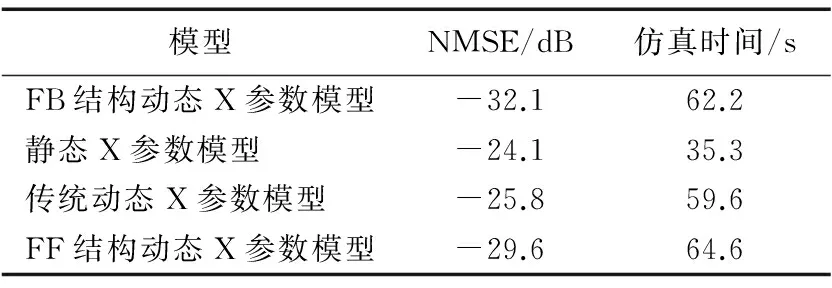
模型NMSE/dB仿真時間/sFB結構動態X參數模型-32.162.2靜態X參數模型-24.135.3傳統動態X參數模型-25.859.6FF結構動態X參數模型-29.664.6

5 結語

考慮功放記憶效應的特點，本文在傳統雙記憶路徑表征功放記憶效應的基礎上，通過改進FB結構并結合動態X參數進一步簡化動態核函數，提出與輸入信號幅度及頻率相關的二維核函數，建立具有記憶效應的非線性射頻功放模型。通過仿真驗證，該模型精確度高，且易實現，為下一步研究系統級仿真以及縮短功放開發提供了一種可能性，但該模型在諧波失配情況下仍需進一步改進。

References)

[1] 袁曉輝.記憶非線性功率放大器行為模型及其數字預失真[D].成都：西南交通大學.2015:2-8. (YUAN X H. Behavioral modeling and digital predistortion of nonlinear power amplifiers with memory effects [D]. Chengdu: Southwest Jiaotong University, 2015: 2-8.)

[2] 林茂六.射頻微波功放器件非線性記憶效應測量與行為建模技術的新進展[J].電子測量與儀器學報,2014,28(2):113-122. (LIN M L. New progress on nonlinear measurement and behavioral modeling for RF power amplifiers with memory effects [J]. Journal of Electronic Measurement and Instrumentation, 2014, 28(2): 113-122.)

[3] JANG H, ZAI A, REVEYRAND T, et al. Simulation and measurement-based X-parameter models for power amplifiers with envelope tracking [C]// MTT ’13: Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest. Piscataway, NJ: IEEE, 2013: 1-4.

[4] 茍元瀟,傅佳輝,林茂六,等.基于矢量測量的射頻微波器件非線性參數化行為建模技術評述[J].儀器儀表學報,2013,34(6):1319-1329. (GOU Y X, FU J H, LIN M L, et al. Review of nonlinear behavioral modeling for RF microwave devices based on vectorial measurement [J]. Chinese Journal of Scientific Instrument, 2013, 34(6): 1319-1329.)

[5] VERSPECHT J, HORN J, BETTS L, et al. Extension of X-parameters to include long-term dynamic memory effects [C]// MTT ’09: Proceedings of the 2009 IEEE MTT-S International Microwave Symposium Digest. Piscataway, NJ: IEEE, 2009:741-744.

[6] VERSPECHT J, HORN J, ROOT D E. A simplified extension of X-parameters to describe memory effects for wideband modulated signals [C]// ARFTG 2010: Proceedings of the 2010 75th Automatic Radio Frequency Techniques Group Microwave Measurement Symposium. Piscataway, NJ: IEEE, 2010:132-136.

[7] VERSPECHT J, ROOT D E, NIELSEN T. Dynamic X-parameters: behavioral modeling in the presence of long term memory effects [C]// GeMiC 2012: Proceedings of the 7th German Microwave Conference. Piscataway, NJ: IEEE, 2012: 1-4.

[8] SOURY A, NGOYA E. Handling long-term memory effects in X-parameter model [C]// MTT ’12: Proceedings of the 2012 IEEE MTT-S International Microwave Symposium Digest. Piscataway, NJ: IEEE, 2012: 1-3.

[9] 田秀華,王振霞,南敬昌.基于功放記憶效應的動態X參數模型的研究[J].計算機應用研究,2016,33(1):71-74. (TIAN X H, WANG Z X, NAN J C. Research of dynamic X-parameter model based on memory effects of power amplifier [J]. Application Research of Computers, 2016, 33(1): 71-74.)

[10] ESSAADALI R, JARNDAL A, KOUKI A B, et al. A new GaN HEMT equivalent circuit modeling technique based on X-parameters [J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(9): 2758-2777.

[11] 李久超,南敬昌,劉元安.通信系統中功率放大器記憶效應的研究[J].計算機仿真,2010,27(7):342-345. (LI J C, NAN J C, LIU Y A. Study of memory effects on power amplifier for communication system [J]. Computer Simulation, 2010, 27(7): 342-345.)

[12] MAZIERE C, SOURY A, NGOYA E, et al. A system level model of solid state amplifiers with memory based on a nonlinear feedback loop principle [C]// Proceedings of the 35th European Microwave Conference. Piscataway, NJ: IEEE, 2005: 853-856.

[13] NGOYA E, MONS S. Progress for behavioral challenges: a summary of time-domain behavioral modeling of RF and microwave subsystems [J]. IEEE Microwave Magazine, 2014, 15(6): 91-105.

[14] QUINDROIT C, NGOYA E, BENNADJI A, et al. An orthogonal lookup-table decomposition for accurate IMD prediction in power amplifier with memory [C]// MTT ’08: Proceedings of the 2008 IEEE MTT-S International Microwave Symposium Digest. Piscataway, NJ: IEEE, 2008:1437-1440.

[15] GUSTAVSEN B. Improving the pole relocating properties of vector fitting [J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1587-1592.

This work is partially supported by the National Natural Science Foundation of China (61372058), the Key Laboratory Project of Higher Education of Liaoning Province (LJZS007).

NANJingchang, born in 1971, Ph. D., professor. His research interests include RF circuit and system, circuit system and electromagnetic simulation, signal processing and information coding.

CUIHongyan, born in 1993, M. S. candidate. Her research interests include RF power amplifier nonlinear analysis, RF circuit design.

ModelingofpoweramplifierbasedondynamicX-parameterofnewtwo-dimensionalkernelfunction

NAN Jingchang, CUI Hongyan*

(SchoolofElectronicandInformationEngineering,LiaoningTechnicalUniversity,HuludaoLiaoning125105,China)

In order to accurately describe the characteristics of Radio Frequency (RF) power amplifier with memory effect, a new dynamic X-parameter amplifier modeling method based on traditional dynamic X-parameter model was proposed by combining with long-term memory effect and short-term memory effect. The new model preserves static kernel function of X-parameter model. A nonlinear function of memory was extracted by using the two-memory path model to replace dynamic kernel function. A novel FeedBack (FB) structure was proposed in which the output signal is a bivariate of amplitude and frequency, and the time-varying frequency variable was introduced to simplify the dynamic kernel function as a two-dimensional kernel function. The power amplifier was designed and modeled by the MW6S010N transistors. Simulation results indicate that the new model can correctly represent the characteristics of power amplifier with the excitation of single-tone large signal and Code Division Multiple Access (CDMA) signal. The Normalized Mean Square Error (NMSE) of the proposed method was decreased by 8.0 dB, 6.3 dB and 2.5 dB, respectively, in comparison with static X-parameter model, traditional dynamic X-parameter model and FeedForward (FF) structure X-parameter model. It is proved that the proposed model can more accurately fit the characteristics of power amplifier with nonlinear memory effect.

two-dimensional kernel function; dynamic X-parameter; FeedBack (FB) structure; memory effect; power amplifier; behavior model

TN722.7

A

2017- 01- 17;

2017- 03- 04。

國家自然科學基金資助項目(61372058);遼寧省高校重點實驗室項目(LJZS007)。

南敬昌(1971-)，男，河南滑縣人，教授，博士，主要研究方向：射頻電路與系統、電路系統與電磁仿真、信號處理與信息編碼；崔洪艷(1993—)，女，遼寧撫順人，碩士研究生，主要研究方向：射頻功放非線性分析、射頻電路設計。

1001- 9081(2017)08- 2421- 06

10.11772/j.issn.1001- 9081.2017.08.2421