非圓行星齒輪馬達輪系特殊結構的設計

王帥帥，李殿起，汪鵬飛，張少華，魏 爽

(沈陽工業大學 機械工程學院，遼寧 沈陽 110870)

·設計計算·

非圓行星齒輪馬達輪系特殊結構的設計

王帥帥，李殿起，汪鵬飛，張少華，魏 爽

(沈陽工業大學 機械工程學院，遼寧 沈陽 110870)

提出了一種高階非圓行星齒輪馬達，相比于波蘭SOK馬達，高階非圓齒輪馬達徑向力平衡，排量大，脈動小，性能更優。如何確定齒輪副中各非圓齒輪的節曲線和齒廓是設計非圓齒輪的關鍵。本文首先依據非圓齒輪的嚙合原理，得出封閉節曲線的方程式，確定在節曲線上均勻分布的輪齒的位置,并通過利用產形齒輪與非圓柱齒輪嚙合關系來確定非圓柱齒輪的齒廓。通過MATLAB編程軟件對相關參數方程進行相應的計算，快速的計算出準確的非圓齒輪副的節曲線和齒廓。最后用實例驗證了該方法的可行性。

非圓行星齒輪馬達；馬達性能；參數方程；MATLAB

0 前言

非圓行星齒輪馬達是一種新型低速大扭矩馬達，其主要特點包括低速運轉平穩、啟動效率高、轉動慣量小、加速和制動時間短、結構緊湊、布置靈活等。變中心距的非圓行星齒輪副是非圓齒輪馬達的關鍵構件。該齒輪副由非圓太陽輪、非圓內齒圈和圓柱行星齒輪構成。本文將非圓齒輪馬達按照非圓行星齒輪副的結構命名。所謂6-8(4-6)型行星馬達，是指太陽輪節曲線的周期數n1=6(4),內齒圈節曲線的周期數n3=8(6)。對于不同非圓太陽輪節曲線方程從而得到的馬達性能顯然也是不同的。在非圓太陽輪運轉一周的過程中，共有n1n3/(n1+n3)個吸液、排液的過程，n1、n3越大,馬達單位體積排量越大，脈動率越小。因此高階非圓齒輪馬達相比于應用中的SOK馬達，具有更深刻的研究價值。本文以太陽輪的節曲線是高階橢圓，內齒圈的節曲線是周期曲線為研究對象。不僅要確定橢圓齒輪副中太陽輪和內齒圈的齒數z1、z3,行星輪的齒數z2，還要計算出橢圓的中徑Rz和偏心率e。目前存在的文獻中只給出了3-4及4-6型齒輪馬達的上述參數，更高階橢圓齒輪機構無參考資料。為此,本文從已知參數n1、n3出發，結合非圓齒輪的特點，用MATLAB語言求解出所需參數，得到節曲線方程和齒廓的方程。從而得到完整而精確的高階非圓行星齒輪機構。

1 參數求解

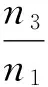
此馬達中的齒輪副的節曲線應該符合以下的要求：

(1)齒輪副要做連續的轉動，來保證周期性的運動關系，因此太陽輪與內齒圈的節曲線都必須是封閉的。

高階橢圓太陽輪的極坐標方程為

(1)

式中,Rz是中徑；e是偏心率；A是橢圓的長軸長度；μ1是向徑r與嚙合點切線的正方向的夾角。內齒圈的節曲線r3的方程為

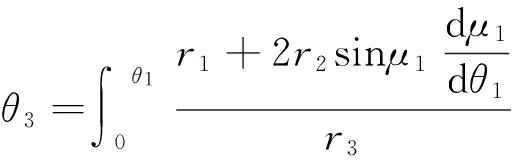
(2)

在φ1=0-2π范圍內，r1變化n1個周期，n1階橢圓的節曲線是閉合的。以n1階太陽輪來計算非圓輪系中內齒圈的節曲線的時候，為了使內齒圈的節曲線封閉，必須滿足條件：

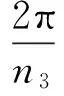
(3)

(2)太陽輪和內齒圈的輪齒均勻分布在各自的節曲線上。

太陽輪(內齒圈)輪齒均布的條件是太陽輪(內齒圈)旋轉2π角度得到的節曲線長度等于πmz1(πmz3)。由以上方程，給出太陽輪和內齒圈的階數n1、n3，行星輪的齒數z2，合適的模數m后，借助MATLAB語言將兩個條件作為約束函數就能得到參數Rz、e。其中，偏心率e的值與模數、齒數無關，對于相同的太陽輪曲邊數，內齒圈的曲邊數與太陽輪的曲邊數差值既n3-n1的值加大時，偏心率應減小。

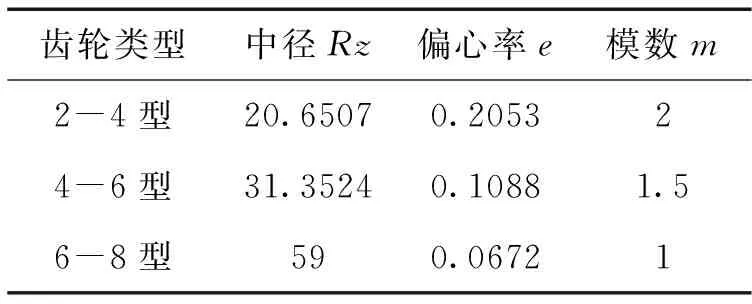
表1 太陽輪的節曲線是高階橢圓時部分參數的搭配

2 非圓齒輪的齒廓及節曲線的確定

2.1 節曲線的形成

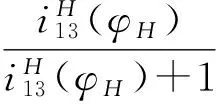
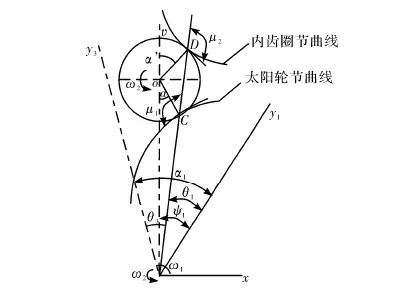
圖1 行星輪系的運動圖

根據已知太陽輪的節曲線來求出內齒圈的節曲線：

太陽輪所在固定坐標系為o1x1y1、o3x3y3是隨同內齒圈回轉的動坐標系。行星輪2的節圓與太陽輪的節曲線在C點接觸，與內齒圈的節曲線在D點接觸。由三心定理，C、D、o1在同一條直線上。對于動坐標系o3x3y3來說，內齒圈滿足的極坐標方程是

(4)

輸入不同的參數Rz、e，太陽輪的階數n1、內齒圈的階數n3，行星輪的半徑r2。通過MATLAB語言分析，就能得到不同非圓行星齒輪副的節曲線。圖2、圖3是分別以4-6和6-8齒輪為算例，得到的節曲線圖形。

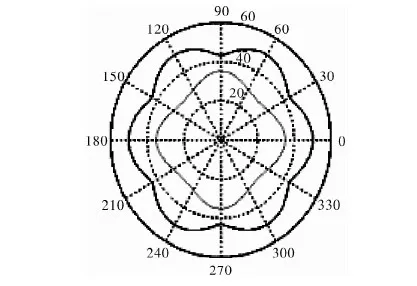
圖2 4-6階非圓行星齒輪副節曲線

圖3 6-8階非圓行星齒輪副節曲線

以6-8階橢圓齒輪副作為算例，圖4～6分別繪制了太陽輪的極徑，內齒圈的轉角、內齒圈角速度與太陽輪轉角的對應關系。

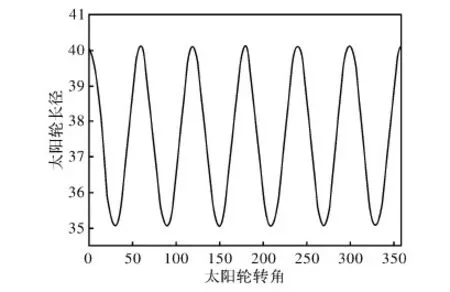
圖4 太陽輪的極徑與太陽輪的轉角之間的關系圖

通過圖4～6可以看出在太陽輪旋轉一周的過程中，太陽輪的極徑以自身階數為周期變化，內齒圈的轉角與太陽輪的轉角關系成立。并且能找出內齒圈的角速度在一個曲線段內變化規律，為齒輪動力學研究提供了方向。同時也驗證了通用程序的可行性。

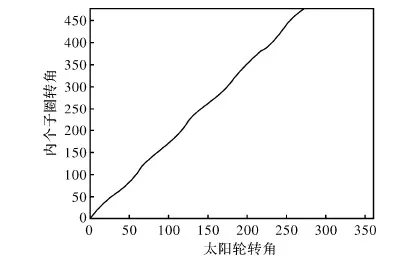
圖5 轉角與太陽輪轉角之間的關系圖

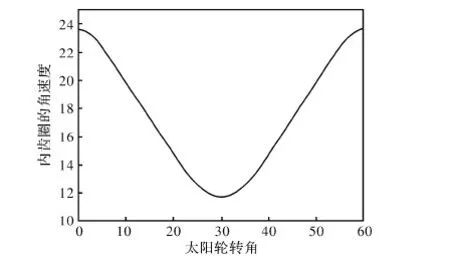
圖6 角速度與太陽輪轉角之間的關系圖

2.2 齒廓的形成

節曲線形狀導致不同的非圓齒輪的齒廓一般也是各不相同的，對于這種節曲線有內凹特點的非圓齒輪,需要用非圓齒輪和產形齒輪內外嚙合來設計這種非圓齒輪的齒廓。

如圖7所示，產形齒輪和非圓太陽輪呈外嚙合狀態，產形齒輪的節圓在太陽輪的節曲線上作逆時針方向的滾動。滾過一定角度后，兩齒輪的節圓在D點接觸。

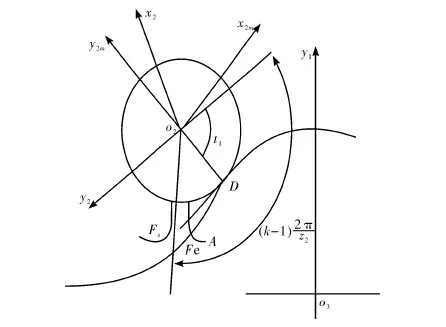
圖7 非圓太陽輪齒廓的形成

坐標系o1x1y1是靜坐標系，坐標系o2x2y2是與產形齒輪副連的的動坐標系。根據求解產形齒輪順時針齒廓的方法。對于順時針齒廓的任意一點Fs，此處對于點的半徑rs為

(5)

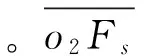
ts=α-αs

(6)

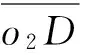
在坐標系o2x2my2m中，Fs的坐標用x2sm和y2sm表示。則在靜坐標系o1x1y1中，Fs點的坐標為

(7)

Fs點的坐標是關于t1的參數方程。當t1由小變大時，嚙合點在太陽輪的齒廓上由齒頂部運動到齒根。另一側齒廓可以采用同樣方法得到。

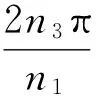
(8)

當非圓行星齒輪應用在液壓馬達上時，可以將節曲線的法向等距線作為太陽輪和內齒圈的齒頂線、齒根線。

3 校檢參數

為保證得到的非圓齒輪副的正確性以及在液壓馬達中的實用性，需要從非圓齒輪的重合度和輪齒在節曲線上的位置兩方面進行驗證。

3.1 校檢重合度

齒根過渡曲線是輪齒干涉分析的基礎，也是求解齒根應力集中系數，進行彎曲強度校核的基礎。對于節曲線是高階橢圓的非圓齒輪，因為將節曲線的法向等距線作為齒頂線和齒根線時存在一定的誤差，所以需要做重合度校驗。非圓齒輪的重合度的公式為

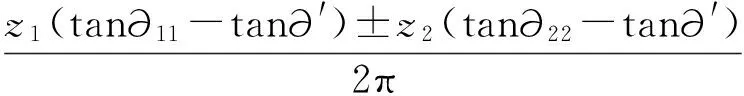
(9)

其中，外嚙合時重合度是正值，內嚙合時重合度是負值。其中，?′是嚙合角，?11、?22是兩齒輪齒頂圓壓力角。通過程序算出6-8行星輪和太陽輪嚙合的重合度最小值是1.4888，并且滿足要求。

3.2 校檢齒輪位置

非圓齒輪上的主、從動輪的節曲線上切點的位置是一一對應的，因此，非圓齒輪的輪齒在節曲線上的位置也是固定不變的。所以有必要判斷MATLAB畫出的齒廓在節曲線上是不是均勻分布的。圖8就是利用MATLAB語言得出的節曲線等分點。

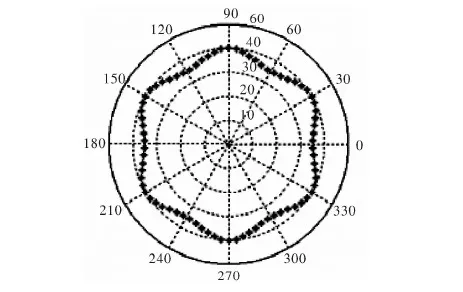
圖8 節曲線的等分點

最后，把得到的節曲線和齒廓數據點導入到SOLIDWORKS進行實體拉伸就能得到圖9所示的高階非圓齒輪副的三維模型。

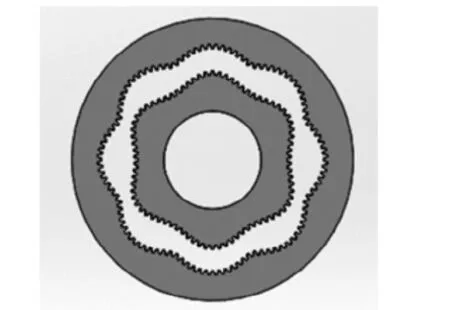
圖9 高階非圓齒輪副的三維模型

4 結論

以非圓齒輪的節曲線和齒廓需滿足的條件為邊界條件，確定出了非圓行星齒輪的中徑、偏心率以及節圓方程和齒廓數據。解決了非圓齒輪參數難以計算的問題。

提出了排量大，徑向力小，振動小的6-8階非圓行星齒輪馬達，突破了以往研究的界限，為高階非圓行星齒輪馬達的發展及應用提供了技術支持。

[1] 許健，許鴻昊. 4-6階非圓行星齒輪系齒數確定的方法[J]. 煤炭學報，2007(03)：23-26.

[2] 廖旋，姚文席.MATLAB在非圓行星齒輪節曲線設計中的應用[J]. 設計與計算，2006(12)：107.

[3] 李建生，李華敏.不同類型非圓行星齒輪液壓馬達的性能分析[J]. 機械傳動，1993，17(02)：1-3.

[4] 王淑杰. 非圓齒輪傳動的快速優化設計[D].合肥工業大學，2005.

[5] 熊鎮芹. 非圓行星齒輪液壓馬達參數設計[J]. 機床與液壓，2004(05)：10-12.

[6] 楊善國，李磊，杜長龍. 非圓行星齒輪液壓馬達的發展及在煤礦機械中的應用展望[J]. 液壓與氣動，2007，(09)：16-18.

[7] 劉生林. 非圓行星傳動研究[J]. 機械設計， 1995(08)：13-14.

[8] 許鴻昊，沈冰妹. 基于雙圓弧節曲線的非圓行星齒輪機構[J]. 煤炭學報，2010，35(04)：691-695.

[9] 何貴平. 內嚙合非圓齒輪加工的數學模型及圖形仿真[J]. 機械設計與研究， 2006,22(04):4-7.

[10] 王昱潭. 新型球面圓弧錐齒輪嚙合原理的研究[J]. 煤礦機械，2011,32(09):10-13.

Design of non-circular planetary gear motor gear with special structure

WANG Shuai-shuai,LI Dian-qi,WANG Peng-fei,ZHANG Shao-hua，WEI Shuang

(Department of Mechanical Engineering,Shenyang University of Technology,Shenyang 110870,China)

A high order non-circular planetary gear motors are proposed in this article. High order non-circular planetary gear motor proves balanced radial force, great motor displacement, small pulsation, which is superior to SOK motor. The key of the gear design is to determine the pitch curve and tooth profile of each non-circular gear. First, based on engagement principle, the pitch curve equation and even-distributed tooth position are obtained. Then, using the engagement gear with non-circular gear in gear forming process, the tooth profile of non-circular can be obtained. The parametric equations of the gear pitch curve and tooth profile are obtained quickly and accurately by MATLAB. Finally, and the feasibility of the method is verified by the actual model.

non-circular planetary gear motor;motor performance;parametric equation

TH132.4

A

1001-196X(2017)05-0059-05

2017-01-06；

2017-03-17

國家自然科學基金(51105257，51310105025)及遼寧省高等學校杰出青年學者成長計劃(LQJ2014012)

王帥帥(1993-)，男，遼寧大連人，沈陽工業大學碩士研究生。