高功率微波作用下等離子體中的雪崩效應研究?

李志剛 程立 袁忠才 汪家春 時家明

(國防科技大學,脈沖功率激光技術國家重點實驗室,合肥 230037)

高功率微波作用下等離子體中的雪崩效應研究?

李志剛?程立 袁忠才 汪家春 時家明

(國防科技大學,脈沖功率激光技術國家重點實驗室,合肥 230037)

研究高功率微波作用下等離子體中的雪崩效應,對于研究等離子體防護技術具有重要意義.通過采用等離子體流體近似方法,建立等離子體中的波動方程、電子漂移-擴散方程和重物質傳遞方程,表征電磁波在等離子體中的傳播以及等離子體內部帶電粒子的變化情況,分析研究了高功率微波作用下雪崩效應的產生過程和變化規律.研究表明,入射電磁波功率決定了雪崩效應的產生;初始電子密度能夠影響雪崩效應產生的時間;入射電磁波的激勵作用初始表現為集聚效應,當激勵能量積累到一定閾值時,雪崩效應才會產生;在雪崩效應產生過程中,等離子體內部電子密度的變化非常迅速并且比較復雜.雪崩效應產生后,等離子體內截止頻率會遠超過入射波頻率,電磁波不能在等離子體中傳播,從而起到防護高功率微波的效果.

電子雪崩效應,等離子體,高功率微波,等離子體防護

1 引 言

高功率微波武器的快速發展給現代戰場中的信息化裝備帶來了極大威脅,尋求有效的防護途徑是亟需研究的課題.當高功率微波入射到等離子體中時,等離子體內部帶電粒子會產生加速運動,吸收電磁波能量,同時,等離子體內部碰撞反應加劇,電子數密度急劇增加,產生雪崩效應,從而屏蔽電磁波的傳輸.利用等離子體的這一特性,通過一定方式在天線或其他電子設備上產生等離子體,可用以進行高功率微波的防護.為此,等離子體高功率微波防護技術得到了廣泛研究［1?3］.

Krlin等［4］研究了高幅值雜波與等離子體相互作用產生的非線性效應;Kikel等［5］提出了等離子體限幅器的概念,并認為可用于電磁脈沖武器的防護;何友文［6］分析研究了高功率微波激勵下的等離子體效應,研究表明高功率微波會被快速激發的等離子體強烈地吸收;楊耿等［7?9］計算分析了在密封腔體中填充Xe氣體的等離子體限幅器的防護性能;舒楠等［10］提出在屏蔽腔中引入等離子體形成雙層屏蔽結構,用以提高屏蔽腔對高功率微波的防護性能;袁忠才和時家明［11］以及劉洋等［12］首先理論分析了高功率微波與等離子體之間的相互作用,然后提出將等離子體陣列結構用于高功率微波防護,并實驗研究了雙層柱狀等離子體對6 GHz高功率微波的防護性能.

高功率微波作用下等離子體內部產生的電子雪崩效應是等離子體產生電磁屏蔽效能的先決條件,研究其產生過程和變化規律對于研究等離子體的防護性能具有重要意義.目前,相關研究還未見全面報道.本文采用等離子體流體近似方法,研究文獻［12］設計的等離子體管防護陣列在高功率微波作用下內部電子密度的變化過程,分別建立了波動方程、電子漂移-擴散方程和重物質傳遞方程來研究高功率微波在等離子體中的傳輸以及等離子體內電子和其他帶電粒子的數密度變化,利用COMSOL軟件的等離子體模塊分析研究了高功率微波作用下雪崩效應的產生過程和變化規律.

2 基本原理

等離子體內部存在著大量的帶電粒子,當電磁波入射到等離子體中時,等離子體中的帶電粒子就會在電磁波的作用下加速運動,電磁波部分能量轉移為帶電粒子內能,電磁波傳輸能量受到衰減;與此同時,帶電粒子的加速運動會導致等離子體內碰撞反應增加,電子數密度增大.當入射電磁波功率足夠大時,等離子體內部就會產生雪崩效應,電子數密度急劇增加,等離子體會對入射電磁波產生屏蔽效應,電磁波無法通過等離子體傳輸.

等離子體流體近似方法是研究和分析等離子體特性時常用的一種方法,即把等離子體做連續的流體束處理,通過求解麥克斯韋方程和流體方程,研究它與電磁場之間的相互作用,以及它在電磁場作用下的變化規律.本文的研究正是基于這一近似方法.首先,建立了等離子體中的波動方程,分析高功率微波在等離子體中的傳播過程;然后,建立了電子漂移-擴散方程,研究高功率微波作用下等離子體內部電子密度的變化情況;最后,建立了重物質傳遞方程,研究等離子體內部其他帶電粒子受入射電磁波的影響.

2.1 波動方程

當電磁波入射到等離子體上時,入射波在等離子體中的麥克斯韋方程［11］為:

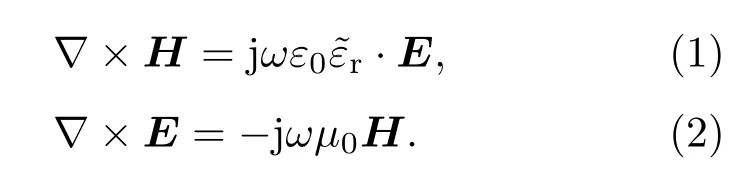
由以上兩式可求得波動方程:

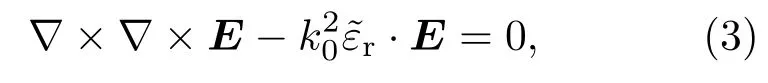
其中,ω為入射電磁波的角頻率,ε0和μ0分為為真空中的介電常數和磁導率,k0為真空中的波數,E為入射場強,?εr為等離子體的相對介電常數,可通過下式求解:

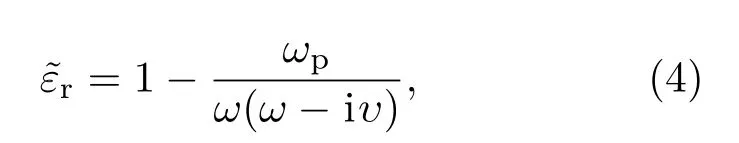
式中,ωp為等離子頻率,υ為電子碰撞頻率.另外,當等離子體可近似處理為一種損耗很低的電介質,可采用電介質模型進行分析;當ω＜υ＜ωp,等離子體可做導電媒質處理,用導電模型分析較合適.

2.2 電子漂移-擴散方程

在外加電磁場的作用下,等離子體內部帶電粒子碰撞頻率增加,電子密度增大.電子密度的變化可通過電子漂移-擴散方程［13］來進行分析,方程可表示為:

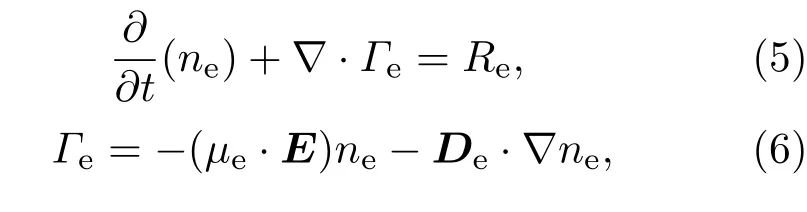
其中,ne為電子密度,μe為電子遷移率,E為入射電場強度,De為電子擴散率;(6)式右側第一項表征的是電子漂移引起的電子密度的變化,第二項表征的是電子密度梯度擴散帶來的電子密度變化;(5)式中Re為電子源項,表征等離子體內部碰撞反應導致的電子的產生與消失,可通過下式求得,

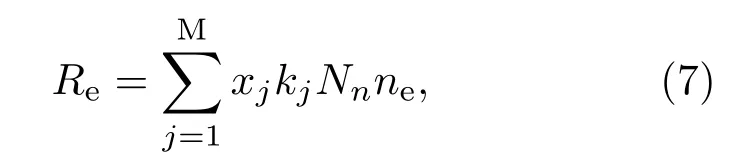
式中,xj為j反應中碰撞粒子的摩爾質量分數,kj為j反應的反應速率,Nn為等離子體中總的粒子數密度.

2.3 重物質傳遞方程

外加電磁場不僅會引發等離子體內部電子密度的改變,也會對其他帶電粒子(包含質子、中子和其他帶電激發離子等)的分布和數密度變化產生影響.這些變化通常可通過求解Maxwell-Stefan方程求得,為計算方便本文通過利用混合物平均模型將Maxwell-Stefan方程進行簡化為重物質傳遞方程［14］:

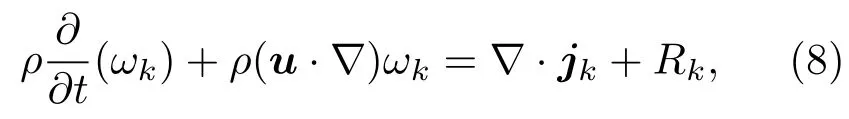
其中,ωk為第k種粒子的摩爾分數,ρ為氣體密度,μ為平均流體速度,jk為第k種粒子的擴散通量,可通過下式表示:

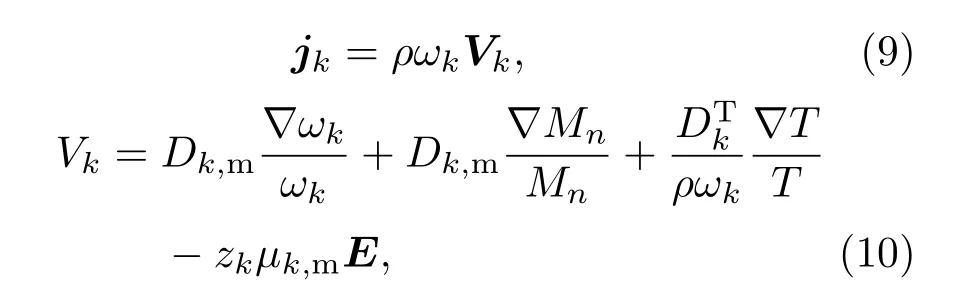
式中,Dk,m為重物質平均擴散系數,Mn為重物質平均摩爾質量,T為氣體溫度,為k種粒子的熱擴散系數,zk為k種粒子的電荷數,μk,m為k種粒子平均遷移率,E為入射場強.

3 計算模型

本文采用COMSOL軟件的等離子體模塊進行分析求解.首先,建立了電磁波激勵模型,如圖1所示,高功率微波垂直入射,對文獻［12］中設計的等離子體管防護陣列(圖2所示)進行激勵.電磁波由上邊界入射,傳播方向為?y方向,經空氣層和等離子體層,傳輸至完美匹配層(PML)后被完全吸收.采用電場分量來定義電磁波的強弱,假設入射電磁波場強幅值為E0,頻率為f;然后,選擇氬氣作為等離子體區域反應氣體,所涉及的粒子種類和碰撞反應在表1給出,氣體溫度設為T,氣體壓強為P.最后,在等離子體區域的外面添加一層玻璃管,對Ar氣體進行封裝,玻璃管的外徑為r1,內徑為r2.左右延伸的等離子體陣列結構是防止電磁波發生繞射,同時,在出射端口設置厚度為d的PML層來保證透射波被完全吸收,下邊界不發生反射.

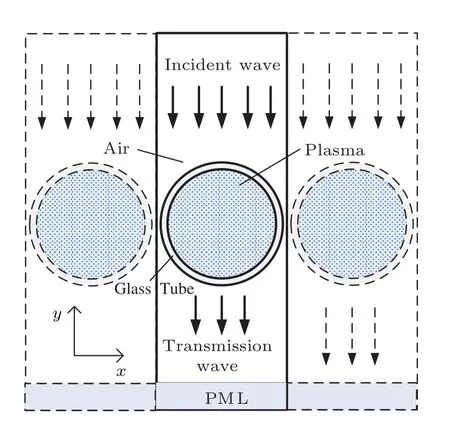
圖1 電磁波激勵示意圖Fig.1.Schematic diagram of electromagnetic excitation.

圖2 等離子體管防護陣列實物圖Fig.2.Photo of the plasma protection array.

在計算過程中,本文設置了不同參數的初始電子密度和入射場強值,研究分析不同條件下電子雪崩效應的產生過程.入射電場波頻率設置為6 GHz,垂直入射,電場強度設為0,0.7×104,1.4×104和2.1×104V/m.氣體溫度設為293 K,壓強設為3 Torr(1 Torr=333 Pa),內部電子分布采用均勻分布(研究發現,初始分布對雪崩效應沒有影響,這與文獻［11］中的結果相一致),初始電子密度分別設置為1.0×106,1.0×109和1.0×1012m?3.玻璃管內外徑分別設為2.5和2.6 cm,計算時間設置為0—1 s.

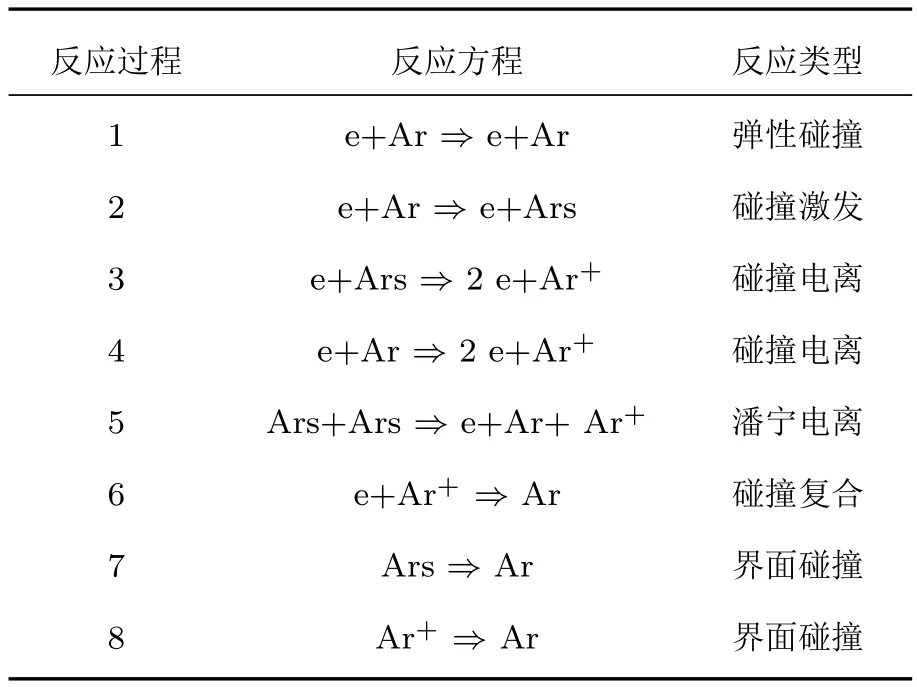
表1 氬等離子體內部碰撞反應方程及類型Table 1.Formula and type of collision reactions inside argon plasma.

4 結果分析

圖3和圖4分別給出了初始電子密度為1.0×106和1.0×1012m?3時等離子體內部平均電子密度在不同入射場強下隨時間的變化情況.從圖中可以看出,當E0為1.4×104和2.1×104V/m的電磁波的照射一定時間后,等離子體內部平均電子密度短時間內急劇增長,電子雪崩效應產生.當E0為0和0.7×104V/m時,在所考慮的時間范圍內,雪崩效應沒有發生.這說明等離子體內部電子雪崩效應的產生具有一定的激勵閾值.

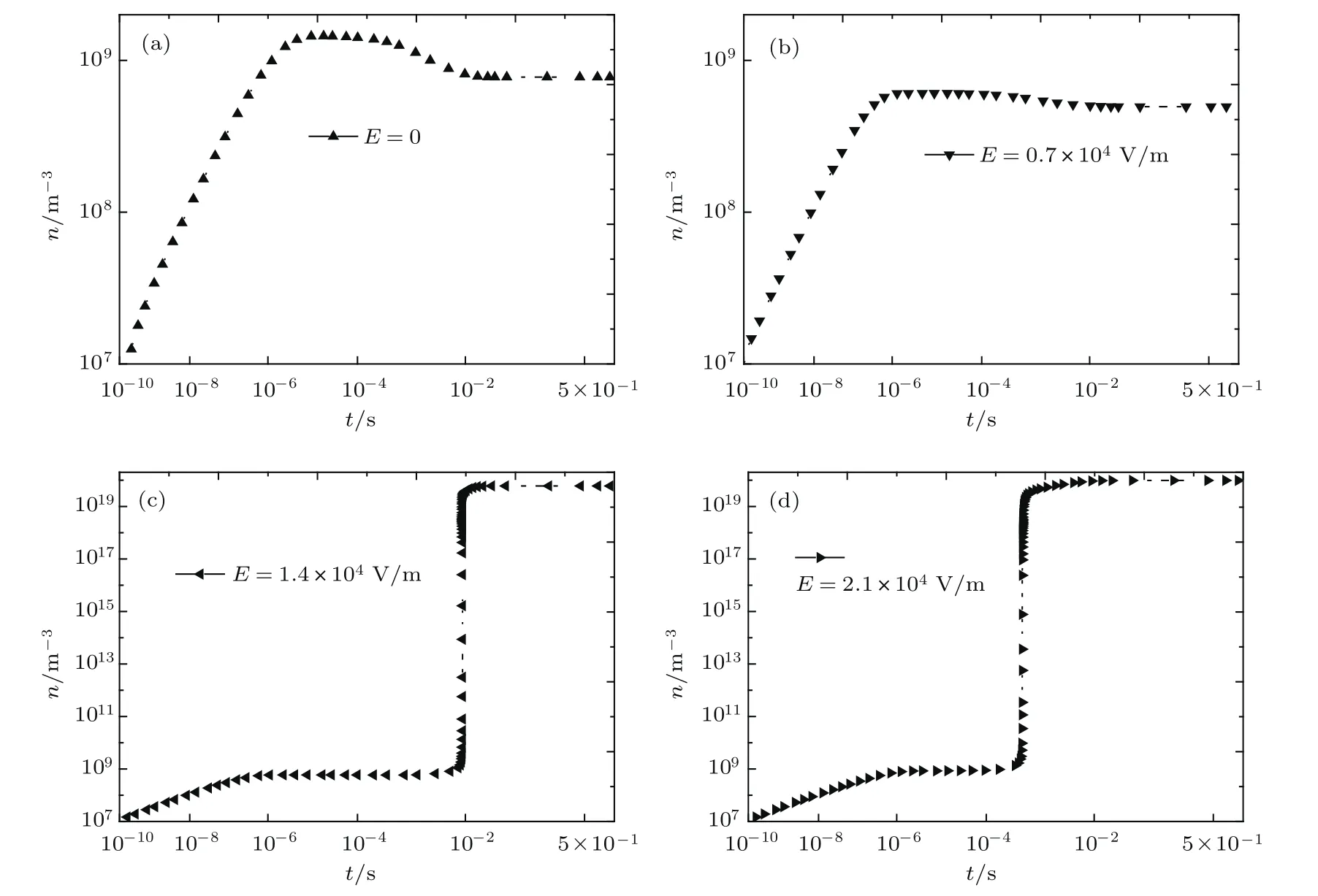
圖3 初始電子密度為1.0×106m?3時,在不同場強作用下等離子體內部平均電子密度隨時間的演變 (a)E0=0;(b)E0=0.7×104V/m;(c)E0=1.4×104V/m;(d)E0=2.1×104V/mFig.3.Changes of the mean electron density under various stresses while the initial electron density is set as 1.0×106m?3:(a)E0=0;(b)E0=0.7×104V/m;(c)E0=1.4×104V/m;(d)E0=2.1×104V/m.

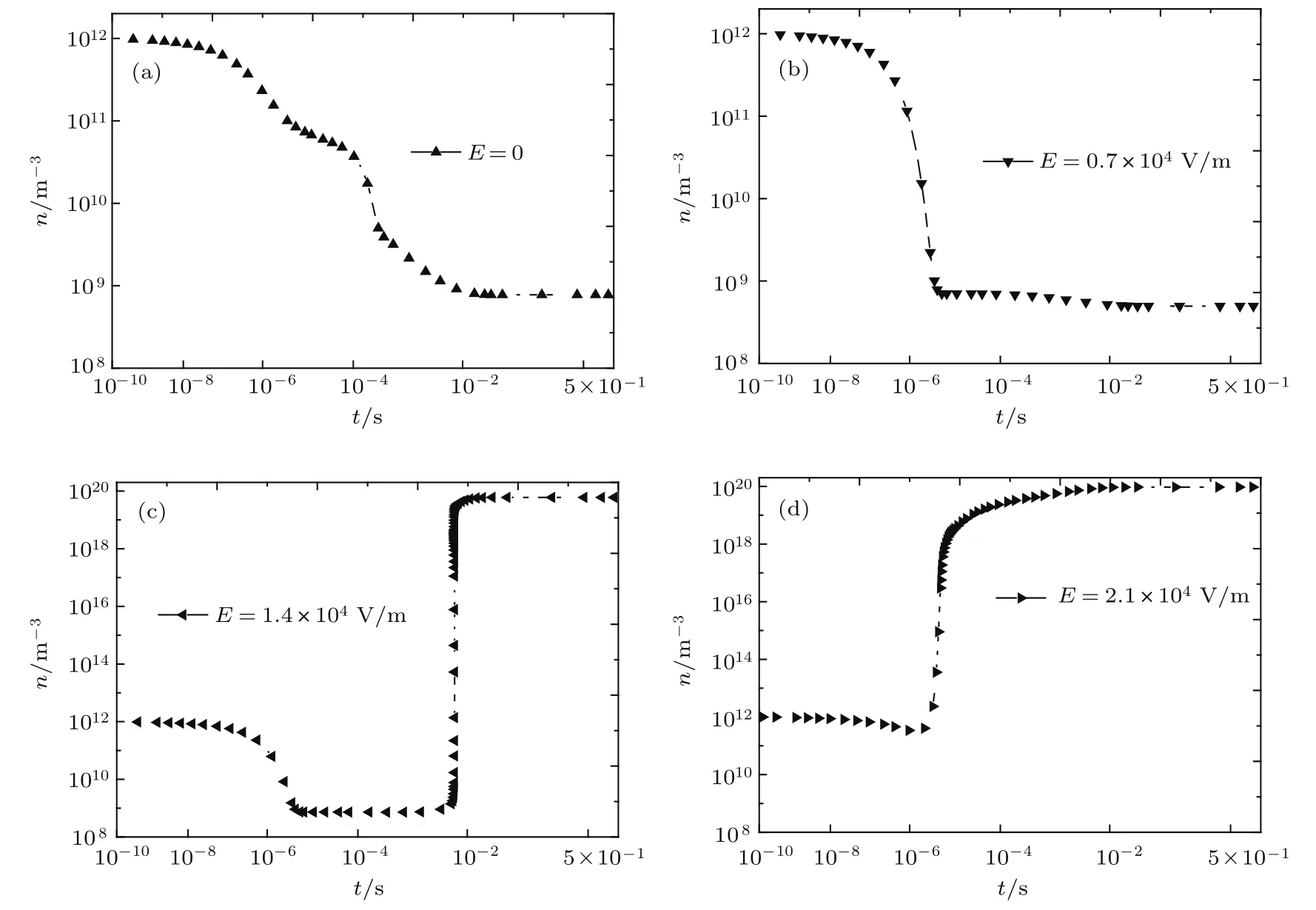
圖4 初始電子密度為1.0×1012m?3時,在不同場強作用下等離子體內部平均電子密度隨時間的演變 (a)E0=0;(b)E0=0.7×104V/m;(c)E0=1.4×104V/m;(d)E0=2.1×104V/mFig.4.Changes of the mean electron density under various stresses while the initial electron density is set as 1.0×1012m?3:(a)E0=0;(b)E0=0.7×104V/m;(c)E0=1.4×104V/m;(d)E0=2.1×104V/m.

當入射場強為0時,等離子體內部平均電子密度的變化可分為兩個階段.第一個階段:在0—0.01 s內,平均電子密度由初始值變化到7.78×108m?3(模型中內部粒子平衡時的平均電子密度約為7.78×108m?3).這一變化是由于初始電子密度設置偏離等離子體內部粒子平衡產生的.等離子體具有強烈的趨于平衡態的傾向,這一趨向主要是通過內部等離子體振蕩和粒子之間的碰撞反應來實現.因此,當初始電子密度為1.0×106m?3時小于平衡態,在很短的時間內,等離子體內電子密度會在內部場作用下不斷增加,當初始電子密度為1.0×1012m?3時大于平衡態,內部電子密度在內部場的作用下逐漸減小,直至達到穩定狀態.第二個階段:在0.01—1 s內,平均電子密度在平衡位置小范圍振蕩,比較穩定.當平均電子密度達到平衡值附近時,等離子體內部的碰撞反應激烈程度衰退,電子產生與消失逐漸達到平衡.

當入射場強為0.7×104V/m時,平均電子密度的變化也可以分為兩個階段:第一個階段與E0為0時相一致,由于初始值偏離平衡態,在內部場的作用下,電子密度逐漸發生改變;第二個階段平均電子密度基本保持穩定,對比圖4(a)可以看出,平均電子密度的振蕩范圍要小很多,這是由于外加電磁場的加入降低了等離子體內部電子碰撞反應的激烈程度.

當入射場強為1.4×104和2.1×104V/m時,平均電子密度的變化可分為三個階段:前兩個階段和E0為0.7×104V/m時完全一致,平均電子密度先向平衡態改變,而后保持穩定;第三個階段產生電子雪崩效應,在極短的時間內,平均電子密度急劇增大,之后建立新的穩態平衡.這一現象說明了外加電磁場的作用表現為集聚效應,在短時間內,它并不改變等離子體內部粒子平衡,而是產生能量積累,當積累到一定程度時,等離子內部平衡被破壞,等離子體區域產生電子雪崩效應.這一現象也從另一個方面說明,等離子體內部會產生一定的平衡勢壘,具有較大的破壞容限,可阻礙或修復外界因素對內部平衡的干擾.在新的平衡下,等離子體平均電子密度約為1×1020m?3,遠大于6 GHz電磁波的截止電子密度(4.464×1017m?3),入射微波無法在等離子體中傳輸,等離子體產生屏蔽作用.這一現象可從電子效應產生前后激勵模型內的電場分布圖中得到,如圖5所示.

另外,從電子雪崩效應的產生過程中,還可以看出初始電子密度的大小對雪崩效應的產生與否影響不大,但增大初始電子密度可以減小雪崩效應的產生時間.外加電磁場功率的大小決定了雪崩效應的產生與否,并且入射場強越大,等離子體就越容易產生電子雪崩效應.

圖6給出了當初始電子密度為1.0×1012m?3,入射場強為1.4×104V/m時,等離子體區域電子密度的空間分布及其隨時間的演變情況,其中,圖6(a)和圖6(b)為效應產生前的電子分布,圖6(c)—(f)為效應產生后的電子分布.圖7給出了等離子體區域中軸線(x=0,y=?0.015—0.015 m)上的電子密度分布情況.從圖中可以看出,電子雪崩效應的產生極為迅速,并且極值分布變化較為復雜.

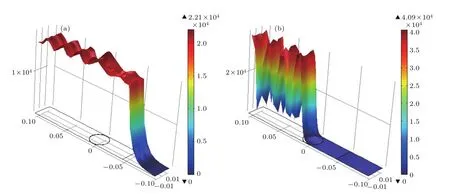
圖5 (網刊彩色)初始電子密度為1.0×1012m?3,入射場強為2.1×104V/m時,不同時刻的激勵模型內電場分布圖(a)t=1.0×10?10s;(b)t=0.01 sFig.5.(color online)Distribution of electric fi eld intensity on the physical model at di ff erent moments while the initial electron density is set as 1.0×1012m?3and the incident strength 2.1×104V/m:(a)t=1.0×10?10s;(b)t=0.01 s.

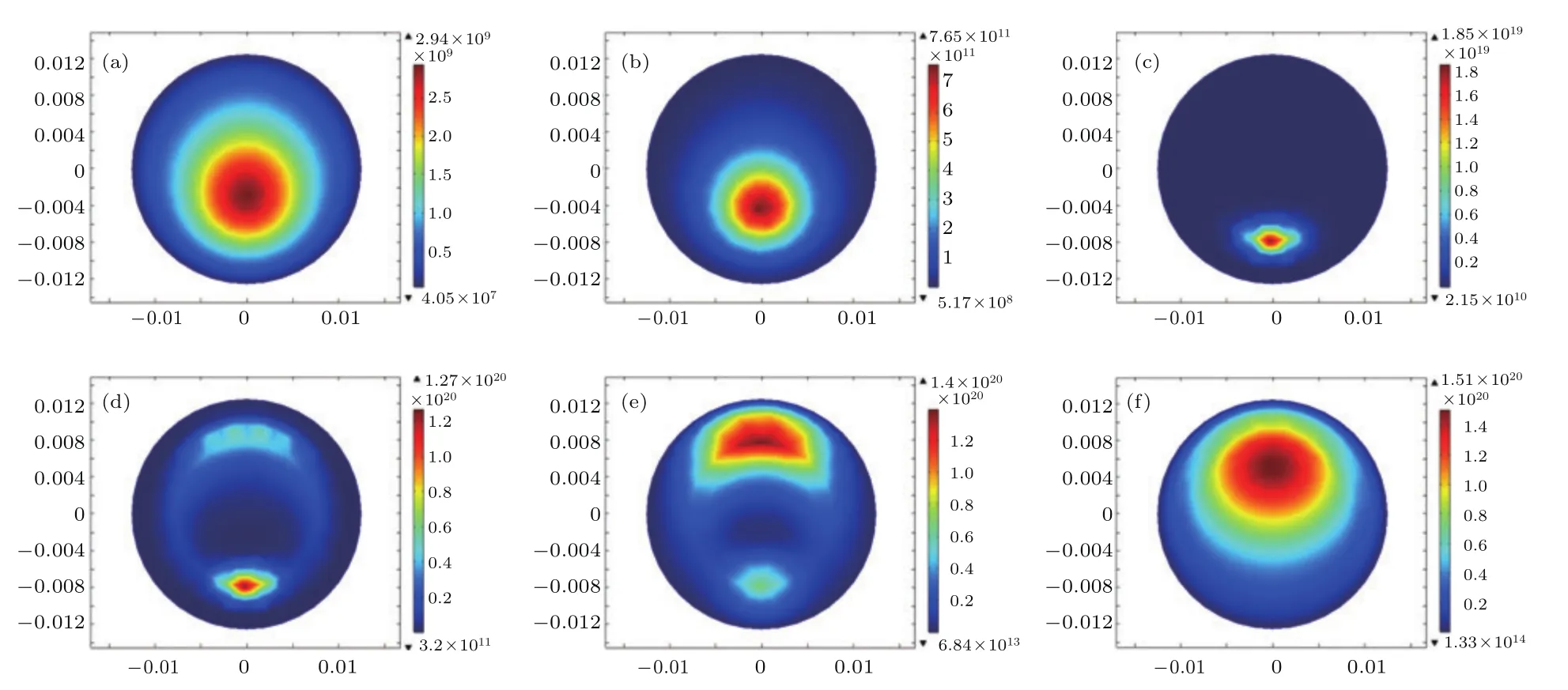
圖6 (網刊彩色)初始電子密度為1.0×1012m?3,入射場強為1.4×104V/m時,等離子體區域電子密度的空間分布隨時間的演變 (a)t=0.004 s;(b)t=0.00617 s;(c)t=0.00618 s;(d)t=0.00621 s;(e)t=0.0064 s;(f)t=0.01 sFig.6.(color online)Distribution of electron density inside the plasma while the initial electron density is set as 1.0×1012m?3and the incident strength 1.4×104V/m:(a)t=0.004s;(b)t=0.00617 s;(c)t=0.00618 s;(d)t=0.00621 s;(e)t=0.00624 s;(f)t=0.01 s.

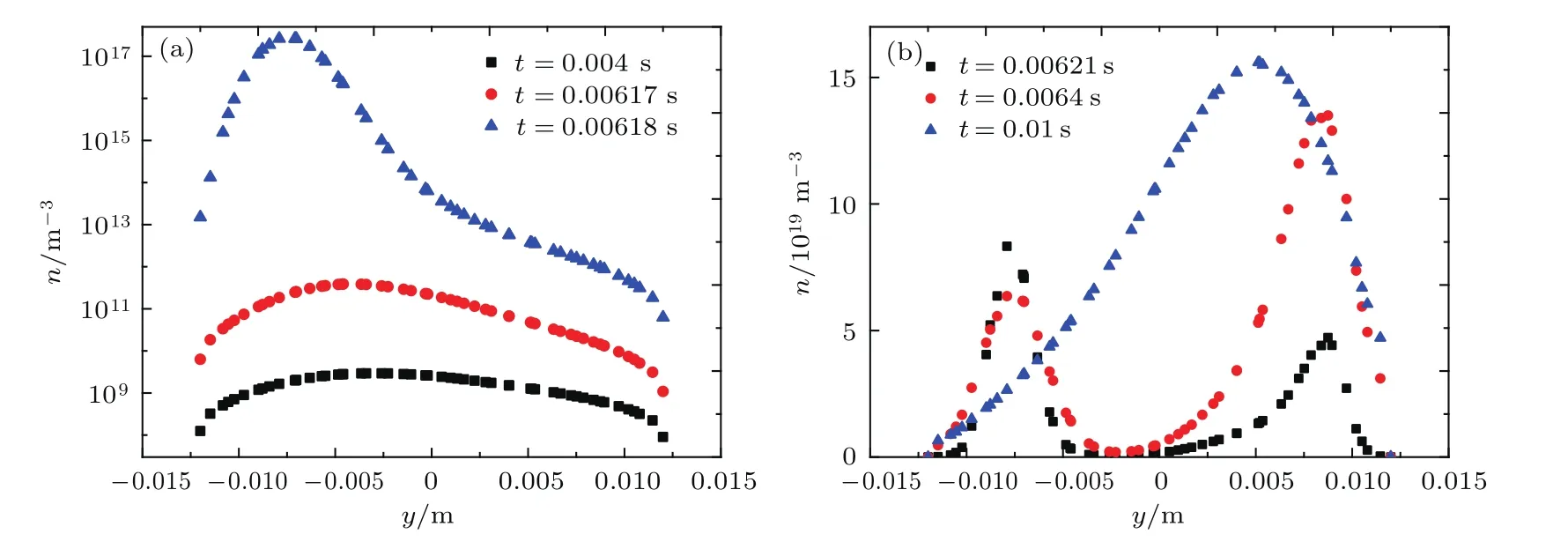
圖7 (網刊彩色)初始電子密度為1.0×1012m?3,入射場強為1.4×104V/m時,等離子體區域中軸線上電子密度的空間分布隨時間的演變 (a)t=0.004 s,0.00617 s,0.00618 s;(b)t=0.00621 s,0.0064 s,0.01 sFig.7.(color online)Distribution of electron density along the axis inside the plasma while the initial electron density is set as 1.0×1012m?3and the incident strength 1.4×104V/m:(a)t=0.004 s,0.00617 s,0.00618 s;(b)t=0.00621 s,0.00624 s,0.01 s.

在雪崩效應產生之前,等離子體區域的電子密度形成以極大值為中心、四周依次遞減的類高斯分布,中心的位置在等離子體中心點偏下的位置(從圖7(a)可以看出極值點在y=?0.004—?0.003 m的位置).隨著外加電磁波的持續激勵,等離子體內的碰撞反應加劇,內部粒子達到的平衡開始被破壞,電子密度增加很快,電子分布也發生了改變,極大值位置沿中軸線遠離中心位置,峰值更為尖銳,從圖7(a)中可以看出t=0.00618 s時刻極值點移動到y=?0.0075 m的位置,極值點更為突出.電子雪崩效應的產生是在峰值處瞬間產生的.雪崩效應產生后,等離子體電子分布發生比較復雜的變化.原峰值處沒有繼續增加和拓展,而在原極值關于等離子體中心對稱處(y=0.008 m處)電子密度開始增加,并且,隨著照射時間的增加,原極值位置電子密度逐漸降低,新極值位置電子逐漸增大到最大值,并且周圍區域電子密度也隨之增加,這反映在圖7(b)中t=0.00621 s和0.0064 s時的變化曲線.總體而言,等離子體區域的電子密度是不斷增加的.最后,原電子密度極值消失,新極值位置向中心偏移(移至y=0.0055 m處),等離子區域形成了以新極值為中心、四周電子密度依次降低的類高斯分布.

產生這些變化的原因,我們認為在于等離子體對入射波的吸收和反射作用.初始時刻,由于內部電子密度較低,等離子體對電磁波的衰減主要以吸收為主,吸收的電磁能量用于提高內部粒子尤其是帶電粒子的內能.相對而言,等離子體上游區域帶電粒子的能量增加也快一些,等離子體區域形成能量梯度,在這一梯度的影響下,內部帶電粒子就會向下游遷移,傳遞能量.在遷移過程中,伴隨著激烈的碰撞反應產生,會有大量新的帶電粒子產生,從而引發連鎖反應.相應區域的電子密度增大,對入射波的能量吸收增大,產生新的能量梯度,帶電粒子繼續遷移,循環往復,直至某一區域(y=?0.0075 m)電子密度開始大于臨界電子密度,等離子體對入射波的反射作用開始顯現.隨著這一區域電子密度急劇增加,入射波大部分能量被反射,并且入射波在模型中形成駐波,在y=0.008 m即距離原中心λ/4處為駐波波峰,該區域吸收大量的電磁能量,大量新生電子在碰撞中產生,電子密度會急劇增大,形成新的極值中心,而原中心會由于入射波被新中心截斷而無法獲得足夠多的維持能量而逐漸衰弱.

5 結 論

采用等離子體流體近似方法,通過建立等離子體中的波動方程、電子漂移-擴散方程和重粒子傳遞方程,研究了高功率微波作用下等離子體管陣列中電子雪崩效應的產生過程及變化規律.研究發現,初始電子密度不會影響雪崩效應的產生,但會影響產生的最小時間,初始密度越大,雪崩效應產生的最小時間越短;入射電磁波功率決定著雪崩效應的產生,入射場強越大,等離子體就越容易產生雪崩效應;高功率微波的照射作用表現為集聚效應,短時間內不會破壞等離子體平衡,當積累一定程度后才會產生雪崩效應;由于內部場的存在,等離子體具有一定的平衡勢壘,可有效消除和修復外界因素對等離子體平衡的破壞;在雪崩效應產生過程中,等離子體內部電子密度的變化非常迅速,而且是比較復雜的.雪崩效應產生后,入射電磁波不能在等離子中傳播,等離子體表現出良好的高功率微波防護性能.

［1］Yu S L 2014J.MicroeavesS2 147(in Chinese)［余世里2014微波學報S2 147］

［2］Lin M,Xu H J,Wei X L,Liang H 2015Acta Phys.Sin.64 055201(in Chinese)［林敏,徐浩軍,魏小龍,梁華2015物理學報64 055201］

［3］Song W,Shao H,Zhang Z Q,Huang H J 2014Acta Phys.Sin.63 064101(in Chinese)［宋瑋,邵浩,張治強,黃惠軍2014物理學報63 064101］

［4］Krlin P P,Panek R,et al.2002Plasma Phys.Control.Fusion44 159

［5］Kikel A,Altgilbers L,Merritt I,et al.1998AIAA98 2564

［6］He Y W 2005Chin.J.Radio Sci.20 392(in Chinese)［何友文2005電波科學學報20 392］

［7］Yang G,An B L,Xue J S 2009J.Microeaves25 74(in Chinese)［楊耿,安寶林,薛晉生 2009微波學報 25 74］

［8］Yang G,Tan J C,Sheng D Y,Yang Y C 2008High Power Laser and Particle Beams20 439(in Chinese)［楊耿,譚吉春,盛定儀,楊雨川 2008強激光與粒子束 20 439］

［9］Yang G,Tan J C,Sheng D Y,Yang Y C 2008Nuclear Fusion Plasma Phys.28 90(in Chinese)［楊耿,譚吉春,盛定儀,楊雨川2008核聚變與等離子體物理28 90］

［10］Shu N,Zhang H,Li G Y 2010Radio Engineer.40 55(in Chinese)［舒楠,張厚,李圭源2010無線電工程 40 55］

［11］Yuan Z C,Shi J M 2014Acta Phys.Sin.63 095202(in Chinese)［袁忠才,時家明 2014物理學報 63 095202］

［12］Liu Y,Cheng L,Wang J C,Wang Q C 2016Chin.J.Luminescence37 1293(in Chinese)［劉洋,程立,汪家春,王啟超2016發光學報37 1293］

［13］Hagelaar G J M,Pitchford L C 2005Plasma Sources Sci.Technol.14 722

［14］He W,Liu X H,Xian R C,Chen S H 2013Plasma Sci.Technol.15 336

Avalanche e ff ect in plasma under high-power microwave irradiation?

Li Zhi-Gang?Cheng LiYuan Zhong-CaiWang Jia-Chun Shi Jia-Ming
(State Key Laboratory of Pulsed Power Laser Technology,National University of Defense Technology,Hefei 230037,China)

High-power microwave(HPM)weapon,which is destructive to electronic systems,has developed rapidly due to the great progress of HPM devices and technologies.Plasma with distinctive electromagnetic characteristics is under advisement as one of potentially e ff ective protection materials.Therefore,research on avalanche ionization e ff ect in plasma caused by the interaction between HPM and plasma is of signi fi cance for its HPM protection performance.Based on the method of fl uid approximation,the wave equation,the electron drift di ff usion equation and the heavy species transport equation,explaining the propagation of microwave and the change of the charged particles inside plasma,are established to study the avalanche ionization e ff ect under the HPM radiation.A two-dimensional physical model is built with the help of software COMSOL according to the plasma protection array designed to disturb the propagation of the HPM pulses.It can be shown that the emergence of avalanche e ff ect is greatly a ff ected by the incident power of microwave,and the generation time would be in fl uenced by the initial electron density.Moreover,it can be observed that the avalanche e ff ect appears only when the plasma array is irradiated for a period of time,which means that the performance of HPM is presented as gathering e ff ect,and a large amount of energy is needed to change the internal particle balance in plasma.In addition,the electron density inside the plasma changes rapidly and complicatedly while the avalanche e ff ect comes into being.Besides,the cuto fffrequency of the plasma exceeds the frequency of the incident wave with the increase of electron density,which leads to that the electromagnetic wave cannot propagate in the plasma,so that the plasma can be used to protect the HPM irradiation.

avalanche ionization e ff ect,plasma,high-power microwave,plasma protection

7 April 2017;revised manuscript

15 July 2017)

(2017年4月7日收到;2017年7月15日收到修改稿)

10.7498/aps.66.195202

?國家高技術研究發展計劃(批準號:2015AA8016029A)資助的課題.

?通信作者.E-mail:class1_48@163.com

?2017中國物理學會Chinese Physical Society

PACS:52.25.Os,52.40.Db

10.7498/aps.66.195202

*Project supported by the National High Technology Research and Development Program of China(Grant No.2015AA8016029A).

?Corresponding author.E-mail:class1_48@163.com