起重量、幅度和起重力矩綜合誤差試驗與數據處理方法分析

陳小平 常振元 王 瑩

(1.安康市質量技術檢驗檢測中心 安康 725000)(2.陜西省特種設備質量安全監督檢測中心 西安 710048)

試驗研究

起重量、幅度和起重力矩綜合誤差試驗與數據處理方法分析

陳小平1常振元2王 瑩2

(1.安康市質量技術檢驗檢測中心 安康 725000)(2.陜西省特種設備質量安全監督檢測中心 西安 710048)

本文基于誤差與數據處理基本理論，對起重量、幅度和起重力矩誤差的關系進行定量分析，對GB/T 28264—2012《起重機械 安全監控管理系統》中三種系統綜合誤差試驗和數據處理方法進行研究，給出利用算術平均值計算同一測試點誤差和取最大誤差測試點的誤差值作為系統綜合誤差的建議。

起重機械 系統綜合誤差 數據處理

起重量、幅度和起重力矩是起重機械的重要設計參數，其綜合誤差試驗方法是我國起重機械檢驗安全技術規范規定的重要檢驗項目[1-2]，在我國起重機械相關標準中也有明確規定[3-4]。國家質檢總局于2012年發布實施了GB/T 28264—2012《起重機械 安全監控管理系統》（以下簡稱“標準”）[5]。標準明確了大型起重機械需要安裝安全監控管理系統，以實現起重機械工作過程重要運行參數和安全狀態的監視、記錄和管理功能。標準對起重機械安全監控管理系統的結構模式、監控信息采集源、監控參數、監控狀態、系統性能要求、試驗方法和系統檢驗等內容做了詳細的要求，標準的發布實施對大型起重機械的安全運行管理有著重要的意義。下面對該標準中有關系統綜合誤差的條款進行幾點思考。

1 三項系統綜合誤差之間的關系

首先應當明確一般意義上的誤差與標準中所述系統綜合誤差的基本概念。一般而言，誤差是指某個測試點實測值與真值之間的偏差，而標準中所述的系統綜合誤差則是指系統顯示數據與被采集信息源的實際數據的最大相對誤差[5]。也就是說，系統綜合誤差是整個量程范圍內相對誤差絕對值最大的測試點的誤差。

然后來看起重量誤差、幅度誤差和起重力矩誤差之間的關系。起重量、幅度和起重力矩三個參數之間具有函數關系，起重量與幅度的乘積就是起重力矩，而幅度和起重量則是彼此相互獨立的兩個參數。根據誤差理論[6-7]，起重力矩的誤差與幅度和起重量的誤差也具有函數關系，即幅度和起重量誤差確定的情況下，可以通過它們與起重力矩的誤差的函數關系計算得出起重力矩的誤差。

一般地，對于函數y = f( x1, x2,…, xn)，若x1, x2,…,xn均為直接測量所得，則y的誤差為Δy：

式中：

Δxi( i = 1, 2,… n )——各個輸入量在該測量點處的誤差；

Δy——變量y的相應誤差；

一般而言，起重量Q和幅度R是由傳感器直接測得的，而起重力矩M則是根據幅度和起重量的實測值計算得出的，即：

根據式(1)有：

化簡得：

式(4)等號兩邊同除以M得：

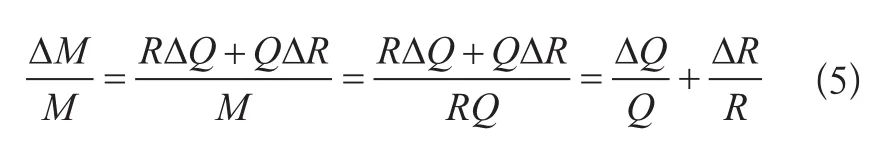
即有：

式（6）中，等號左邊為起重力矩的相對誤差，等號右邊兩項分別為起重量和幅度的相對誤差，也就是說，起重機械力矩曲線上任意一點的起重力矩相對誤差等于相應幅度和起重量相對誤差之和。

2 幅度綜合誤差

2.1 標準的要求

標準7.2規定起重機械幅度綜合誤差的試驗方法為，空載狀態下，分別選擇0.3R、0.6R、0.9R作為幅度測試點(R為起重機械的最大工作幅度)，變幅機構在測試點附近小范圍內來回運行兩次后停止，測定實際幅度R0.3、R0.6、R0.9，并讀取系統的顯示值，分別計算三次測試中幅度實測值和顯示值的算術平均值Ra和Rb，綜合誤差按式(7)計算：

式中：

ER——幅度綜合誤差；

Ra——3次幅度實測值的算術平均值，m；

Rb——對應3次幅度顯示值的算術平均值，m。

由上述試驗計算方法可知，幅度綜合誤差的計算方法為：首先分別求出30%、60%、90%工作幅度下3次試驗實測值和顯示值的算術平均值，然后帶入式(7)進行計算，得出幅度綜合誤差值。

2.2 分析與建議

標準中所述的幅度綜合誤差，實質上是起重機械安全監控管理系統的幅度最大允許誤差。通常測量裝置的最大允許誤差用引用誤差或相對誤差來表示[8]，由標準中規定的試驗計算方法可以看出，幅度綜合誤差采用幅度的相對誤差來描述。即起重機械幅度的綜合誤差為起重機械整個幅度范圍內的最大絕對誤差與該處幅度實測值的比值乘以100%。

眾所周知，測量裝置和儀器量程內各點的相對誤差是不同的，也即測量精度不同。根據誤差理論，不等精度測量的數值是不能夠簡單相加后取算術平均值的，而應當根據情況對各個實測值賦予不同權重后再進行運算，才能夠得出正確的結果[9]。對于同一測試點的實測值計算屬等精度測量，在剔除測量的粗大誤差后，可以將實測值的算術平均值作為約定真值。通常有效實測值相對偏差在0.2%～0.4%之間[10]。標準給出的試驗計算方法中取3個不同幅度測試點進行測量計算，由于3個不同幅度處的測量真值不同，同樣大小的絕對誤差對應的相對誤差不同。因此，標準中關于幅度綜合誤差的計算方法是值得商榷的。建議幅度綜合誤差的試驗計算方法如下：

空載狀態下，分別選擇0.3R、0.6R、0.9R作為幅度測試點(R為起重機械的最大工作幅度)，變幅機構在測試點附近小范圍內來回運行兩次后停止，作為一次幅度測試。在每個幅度測試點分別測量三次并取算術平均值，記為R1a、R2a、R3a。相應地，讀取每個幅度測試點的三次幅度顯示值，取其算術平均值，記為R1b、R2b、R3b。分別計算出各測試點處幅度的誤差E1R、E2R、E3R，取各測試點誤差中絕對值最大的測試點的誤差值作為幅度綜合誤差值。各測試點的幅度誤差按照式(8)計算。

式中：

EiR——相應測試點的幅度誤差；

Ria——相應測試點三次幅度實測值的算術平均值，m；

Rib——相應測試點三次幅度顯示值的算術平均值，m；

i——測試點編號，i=1，2，3。

需要指出的是，按照標準給出的方法僅能得出一個綜合誤差值，且在計算公式中加入了絕對值符號，使得計算出的綜合誤差數值始終大于0；而本文建議的試驗計算方法可分別得到三個測試點的幅度誤差值，且無符號限制，在實際應用中能夠反映出測量裝置誤差在各個測試點的大小方向分布情況，更有利于尋找測量裝置在整個量程內的誤差分布規律，進而可采取適當的方法減小測量裝置的誤差。因此，本文所述方法更加合理一些。

2.3 舉例

某塔式起重機，最大幅度R=70m，分別在21m、42m和63m處按照2.2所述方法測量幅度值，幅度實測值與顯示值及其偏差計算見表1。

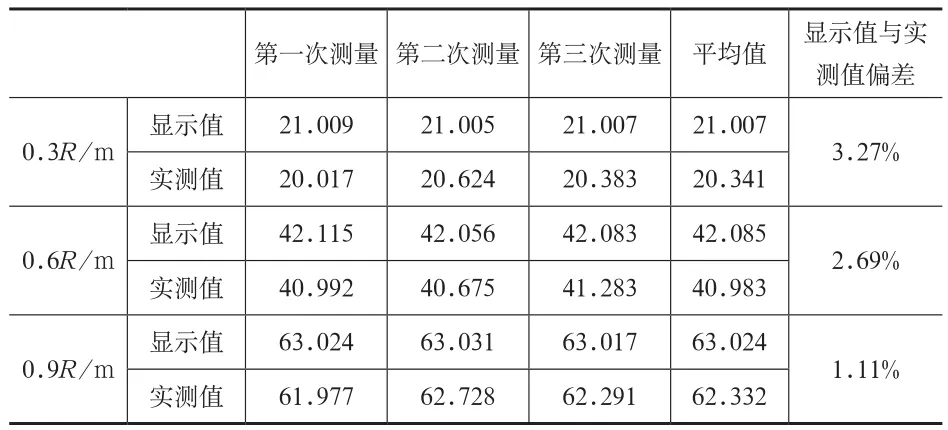
表1 幅度綜合誤差測量數據表

由表1可知，0.3R、0.6R和0.9R處幅度的顯示值與實測值的偏差分別為3.27%、2.69%和1.11%，系統幅度綜合誤差取三處偏差的最大值為3.27%。

3 起重量綜合誤差

3.1 標準要求

標準7.1條起重量綜合誤差的試驗計算方法作出規定，要求至少有三個測試點，每次測試所用載荷不低于0.3倍的額定起重量。額定起重量作為一個測試點，其他兩個測試點在0.3倍額定起重量和額定起重量之間任意選取。綜合誤差按式（9）計算：

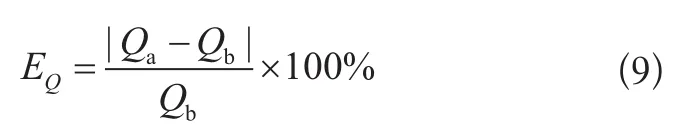
式中：

EQ——起重量綜合誤差；

Qa——系統顯示數據，t；

Qb——試驗載荷的實際數據，t。

3.2 分析與建議

標準僅要求起重量綜合誤差試驗時至少取3個測試點進行，但沒有明確各次試驗所得到的多個起重量實測值和顯示值如何進行數據處理后，才能帶入綜合誤差計算公式進行計算。

建議利用本文2.2節所述的方法進行起重量綜合誤差數據的處理與計算，具體過程舉例不再贅述。

4 起重力矩綜合誤差

4.1 標準要求

標準7.3條規定起重力矩綜合誤差的試驗計算方法為：在力矩曲線范圍內選能代表幾種力矩變化特性的3點作為檢測點，綜合誤差按式（10）計算：

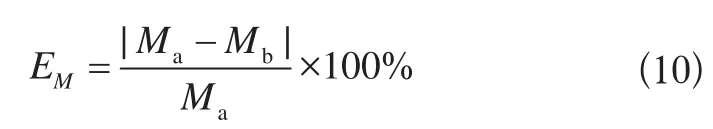
式中：

EM——起重力矩綜合誤差；

Ma——實際力矩，kN·m；

Mb——對應的起重力矩顯示值，kN·m。

4.2 分析與建議

標準起重力矩試驗時要根據力矩特性曲線選取3個能代表力矩特性的檢測點，未說明3個點檢測實測值如何獲得，是測出幅度和起重量值后將兩者相乘計算出力矩實測值還是用其他方法直接測出起重力矩，無從知曉。另外，標準也沒有說明如何對3個力矩檢測點的實測值和顯示值進行數據處理，從而得到綜合誤差公式中的力矩實測值和顯示值，繼而求得起重力矩的綜合誤差。

本文建議起重力矩的綜合誤差試驗及數據處理計算采用2.2節分析所述的方法進行，具體為：根據系統力矩特性曲線選取3個能代表力矩特性的檢測點，查找3個檢測點相應的幅度和起重量。對于每個檢測點按照相應的起重量在相應幅度下各進行3次加載試驗，取得每次試驗幅度和起重量的實測值和顯示值。根據本文所述方法分別計算出3個測試點幅度和起重量的誤差，利用起重力矩誤差傳遞函數公式分別計算出3個測試點的起重力矩誤差，取其絕對值最大的測試點的誤差值作為起重力矩的綜合誤差。

5 結論

通過起重力矩、幅度和起重量誤差的關系定量分析可知，起重力矩的誤差等于兩者誤差之和。多組起重量、幅度和起重力矩實測值和顯示值的數據處理，不能簡單地進行算術平均。對于同一測試點的多次重復測量為等精度測量，可以取多個實測值的算術平均值與顯示值的相對偏差作為該測試點的誤差；分別計算各測試點的誤差，絕對值最大的測試點的誤差即為起重量或幅度的綜合誤差；在力矩特性曲線上選取合適的測試點，分別試驗計算各測試點處相應的幅度和起重量誤差，再利用誤差傳遞函數計算出各測試點的起重力矩誤差，絕對值最大的測試點的誤差值即為起重力矩的綜合誤差；本文的方法可以得到三個測試點誤差的大小和方向，更有利于尋找測量裝置在整個量程內的誤差分布規律，進而可采取適當的方法減小測量裝置的誤差。

[1]TSG Q7015—2016 起重機械定期檢驗規則[S].

[2]TSG Q7016—2016 起重機械安裝改造重大修理監督檢驗規則[S].

[3]GB 12602—2009 起重機械超載保護裝置[S].

[4]岳維峻.起重力矩限制器生產現狀及其調試[J].建筑機械化，2006，(07)：37-38.

[5]GB/T 28264—2012 起重機械 安全監控管理系統[S].

[6]費業泰.誤差理論與數據處理[M].北京：機械工業出版社，2015.

[7]卜雄洙.工程測量誤差與數據處理[M].摩客譯.北京：國防工業出版社，2015.

[8]JJF 1094—2002 測量儀器特性評價[S].

[9]John Taylor.誤差分析導論 物理測量中的不確定度[M].王中宇譯.北京：高等教育出版社，2015.

[10]李靜.儀器儀表的精確度分析[J].中國科技博覽，2015，(07)：268-268.

Analysis of Comprehensive Error Test and Data Processing Method of the Load Radius and Crane Torque

Chen Xiaoping1Chang Zhenyuan2Wang Ying2
(1. Ankang Quality and Technical Inspection Testing Center Ankang 725000)(2. Shannxi Special Equipments Inspection Center Xi’an 710048)

In this paper, based on the basic theory of error and data processing, the quantitative analysis about the relationship of the error of the load, radius and crane torque is taken, and three kinds of system comprehensive error test and data processing method in GB/T 28264—2012 Lifting appliances—Managing System of Safty Monitoring are researched, the arithmetic mean used to calculate the same test point error and the maximum error of test points as system comprehensive error is given.

Crane Comprehensive error Data processing

X941

B

1673-257X(2017)09-0014-04

10.3969/j.issn.1673-257X.2017.09.004

陳小平（1967～)，男，大專，總檢驗師，工程師，從事機電類特種設備檢驗工作。

常振元，E-mail： 13759928369@139.com。

2017-01-18）