建模思想在小學數學中的應用

任紅君

[摘 要]

要解決一道復雜的數學問題，關鍵就在于思想方法的運用，而思想方法的核心就是建立模型，它是問題解決的最重要組成部分，體現了學生的學習能力。本文簡要提出模型構建的3個重要步驟，并以小學常見的數學類型題為例，通過列舉幾種基本的數學模型，強調用模型解題的簡便性，突出建模思想在小學數學學習中的重要地位。

[關鍵詞]

小學數學；數學建模；模型思想

一、模型的構建

小學的數學問題，多半是數學知識與實際情況相結合產生的。一部分包含生活實際，一部分聯系數學專業知識。而數學建模思想就是根據問題中所描述的復雜的已知條件，通過分析問題本質，化繁為簡，抽取有用的數學信息，從而把生活情境轉化為數學符號或圖像，并用數學文字來表示問題的過程。小學學習的數學知識是數學領域最根本的知識，因此在日常數學教學過程中，除了讓學生領會課本上的知識以外，教師更應該培養學生的思維方式和解決問題的能力，為以后初中和高中的學習打下堅實的基礎。

（一）創設情境，激發興趣

教師在平時的課堂教學中，可適當地向學生們提出一些他們平時會碰到的問題。比如幫父母賣水果、讓學生計算從家到學校的距離、判斷東西是否會按時送達等。通過講述一些身邊發生的情況，激發學生興趣，并逐漸上升到數學問題。通過觀察、比較、分析、綜合、抽象概括等方式，尋找必要條件，聯系已學知識，建立數學模型，形成初步的建模思想觀念，通過數學建模，使小學生真正感受到數學知識與外部世界的聯系，激發學習興趣。

（二）找出問題本質，完成模型構建

具體的情境能夠激發學生對問題的興趣，但如果沒有將具體情境轉化為抽象數學知識，那就無法完成建模。以“圓的認識”為例，如果只是讓學生感知象棋、鐘表、車輪等具體的生活素材，而忽略尋找它們本質的過程，那么，當學生提取“圓”的模型時，呈現出來的一定是生活中圓形的具體實物，而不是數學意義上的圓。因此，教師在教學過程中，應當注重培養學生找出問題本質的能力。從而建立真正意義上的數學模型，完成從具體到抽象的數學模型的構建過程。

（三）拓展模型，回歸生活

從具體情境中構建抽象的數學模型，再將已構建的模型應用到實際生活中，是完整的模型構建的過程。通過將模型還原為具體可感的數學實際問題，使已經構建的模型得到擴充和提升。如經典的“雞兔同籠”問題模型就是通過研究“雞”“兔”建立起來的，而這個模型也可以用到許多實際問題中去。例如：自行車與小轎車一共有20輛，它們一共有64個輪子。問自行車有多少輛？小轎車有多少輛？這樣通過解答不同的問題，使模型得以拓展和擴充。

二、模型的應用

數學模型，一般來說，就是根據某種事物的特征或數量關系，采用形式化的數學符號和語言，來表示問題的一種特殊的數學結構。在小學數學的學習過程中，許多內容的本質就是數學模型。比如：一年級下冊書中講述過的圓角分的計算，其數學模型實際上就是小數的運算；還有在奧數比賽中經常會遇到的雞兔同籠問題，其數學模型實質上就是二元一次整數方程。更進一步來說，解決一道數學應用題，就是對一種比較復雜抽象的特定情境用數學符號簡化成一個具體的模型。本文根據小學數學應用題的不同類型總結了幾種常見的數學模型。

（一）數學文字模型

數學文字型應用題，顧名思義，就是純文字的一類應用題。這類應用題通常比較復雜抽象，且無關的條件較多。建立文字型數學模型，就是將數學應用題里一些可以忽略的無用條件去掉，將原題改寫成只有數學文字表達的模型。經過這樣的改變后，應用題的條件和問題都變得一目了然，解題思路也變得清晰許多。舉一道小學常見的應用題為例：

例1：小華、小明、小剛三個同學共有45個蘋果。如果小華向小明要了三個蘋果，然后又送給小剛5個。那么現在三個人擁有的蘋果數量恰好相同。問：小華、小明、小剛三個同學原來各擁有多少個蘋果？

分析：根據題意，將有用的數學信息抽取出來，用相應的數學文字模型表達。三個同學之間給來給去，沒有給別人。那么三個同學擁有的蘋果數相同，也就是現在每個同學有45÷3=15（個）。因為小華向小明要了3個蘋果后，小明有15個蘋果。則原來小明的蘋果數為15+3=18（個）。又因為小華給了小剛5個蘋果后，小剛有15個蘋果，則小剛原來擁有蘋果數為15-5=10（個）。則小華擁有的蘋果數為45-18-10=17（個）。這樣，通過將生活中常見的字眼“要”“送”等轉化為數學中的“多”“少”，再進一步簡化為“+”“-”，就建立起了簡單的數學文字型模型。通過建立模型，使解題變得簡單許多。

（二）圖式模型

圖式這一概念最初是由康德提出的。康德認為圖式是“潛藏在人類心靈深處的”一種技術、一種技巧。在小學數學學習過程中，教師應不斷地引導學生應用圖式模型解決數學問題。建構數學學習圖式，有利于找準問題的難點，化繁為簡、化難為易；有利于解決數學學習中的困難；有利于學生形成自己獨特的知識體系，把腦海中的知識點連成一條線，進而形成自己的知識網絡。以一道典型的線段圖為例：

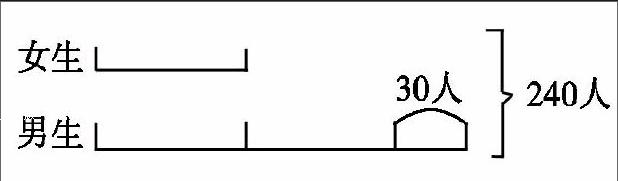
例2：某校五年級學生一共有240人。其中男同學的人數比女同學人數的2倍還多30人。問學校五年級男生有多少人？女生有多少人？

分析：將女同學的總人數看作1份，則男同學的人數是2份+30，由此得到模型

通過線段模型，可以很清楚地看出：女生的人數為（240-30）÷3=70（人）男生的人數為70×2+30=170（人）。

（三）算數模型

算數方法是小學生最先接觸的解題方法。在訓練學生的獨特思維和對數量關系的分析方法上，算數方法是不可替代的。以大家熟悉的問題為例：

例3：在下面空白處填上合適的數。

（1）2，5，8，11， ，17，20……endprint

（2）5，10，15，20， ，30，35……

（3）1，3，4，7， ，18，29……

分析：通過閱讀此題，我們能夠知道問題中的數與數之間有一種關系。通過觀察三個小問題，我們能夠直觀地看出（1）中后一個數比前一個數大3，容易求得（1）空白處的數字為11+3=14，而14也正好比后一項的數字17小3。在（2）中顯然數和數之間不是一種加法關系，第1個數為5×1，第2個數為5×2，通過歸納總結，可以得出第N個數為5×N。所以當N為5時，得出（2）中第5個數為5×5=25。再觀察（3），雖然不能直接看出數與數之間的關系，但通過前后數字的作和，可得出這樣的關系式：1+3=4，3+4=7，經過總結，我們能夠發現數與數之間奇妙的關系，即：前兩個數的和等于后一個數。求得空白處的數字為4+7=11。在解決一些問題時，通過建立算數模型，能夠很容易找到這些看似雜亂的數字之間的聯系。

（四）分類模型

在小學數學教學過程中，教師應積極培養學生的模型意識。使學生在面對復雜問題時，能夠第一時間從腦海里找到此類問題所對應的數學模型。小學數學中絕大多數復雜的應用題，我們都可以從中找到一個甚至幾個數學模型。也就是說，一些較為復雜的數學模型往往是由幾個簡單的基礎模型組成的。因此，熟練理解并運用基本模型解決問題就變得尤為重要。本文總結了幾個在小學數學應用題中常見的基礎模型：

三、結語

不同于中學、大學旨在培養數學高素質人才的遠大目標，建模思想在小學階段的應用主要在于培養學生的學習能力、思維能力、學習興趣，使學生在遇到復雜問題時，能夠主動運用建模思想來解決問題、分析問題，形成積極正確的學習態度。《課程標準》曾明確說明：“模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑。”也就是說，建立數學模型的最基本的目的，就是讓學生從數學的角度看待外部世界，理解數學與外界的基本聯系。從根本來說，擁有建模意識，可以使學生在分析問題時更接近問題的本質，從而考慮問題更精確、更全面。因此，數學建模思想在小學數學中的應用顯得尤為重要。

[參 考 文 獻]

[1]姜啟源.數學建模[M].北京：北京高等教育出版社，1993.

[2]李羅平.淺談小學數學建模在數學活動中的運用[J].新課程學習（中），2012（10）.

[3]陳蕾.小學數學建模的三個關注點[J].上海教育科研，2013（8）.endprint