GPS失鎖情況下基于神經網絡的組合導航算法研究*
張新民, 張 維
(北京航天自動控制研究所, 北京 100854)
GPS失鎖情況下基于神經網絡的組合導航算法研究*
張新民, 張 維
(北京航天自動控制研究所, 北京 100854)
文中針對GPS/SINS組合導航系統中GPS信號失鎖問題進行研究,采用基于神經網絡的組合導航算法。在GPS信號失鎖時間段內,用神經網絡模擬GPS的信息,進行信息融合。文中給出了基于神經網絡的組合導航系統模型,并進行了數學仿真研究,結果表明,引入了神經網絡的組合導航系統,在GPS信號失鎖時,能保證一定的導航精度。本文為組合導航系統中GPS信號失鎖問題的解決提供了一種方法。
組合導航;神經網絡;GPS信號失鎖
0 引言
GPS和INS具有優勢互補的特點,基于GPS/INS的組合導航系統在工程中廣泛應用。但當載體的高動態運動或受到外界干擾時,常引起GPS信號失鎖,組合導航系統將無法正常工作。隨著系統對導航精度要求的不斷提高,GPS信號失鎖問題越來越受到重視。
神經網絡(neural network,NN)作為一門發展了半個多世紀的技術,隨著各種神經網絡理論模型和學習算法的提出,神經網絡理論已日趨成熟。文中將神經網絡人工智能技術引入到組合導航系統信息融合算法中,改善GPS信號失鎖時組合導航系統的連續性,提高導航精度。
1 GPS/SINS組合導航系統
文中基于位置、速度匹配的淺組合模式,采用卡爾曼濾波方法,對系統誤差進行間接估計。下面給出該模式下的狀態方程和量測方程。
1.1 組合導航系統的狀態方程
選東北天坐標系為導航坐標系。狀態方程為:

(1)
式中:XI(t)∈R18為狀態變量;FI(t)∈R18×18為系統矩陣;WI(t)∈R9×1為系統噪聲向量;GI(t)∈R18×9為系統噪聲矩陣。
狀態變量為:
XI=[ABCDEF]
其中:A=[φEφNφU]
B=[δvEδvNδvU]
C=[δLδλδh]
D=[εbxεbyεbz]
E=[εrxεryεrz]
F=[xyz]
式中:下標E、N、U分別為東北天方向;下標x、y、z分別代表載體系橫向、縱向和天向。φE、φN、φU為平臺誤差角;δvE、δvN、δvU為速度誤差;δL、δλ、δh為位置誤差;εbx、εby、εbz為沿載體系的隨機漂移;εrx、εry、εrz為陀螺一階馬爾可夫誤差;x、y、z為加速度計偏差。
FI為18×18維的矩陣,表達式為:
式中:FN矩陣為典型的9×9的慣導系統誤差矩陣;FS是基本導航參數與慣性器件誤差之間的轉換矩陣;FM是慣性器件誤差矩陣[1]。
系統噪聲向量為:
WI=[ωgxωgyωgzωbxωbyωbzωaxωayωaz]T
式中:ωg為陀螺白噪聲項;ωb為陀螺一階馬爾可夫噪聲項;ωa為加速度計白噪聲項。
系統噪聲矩陣為:
1.2 組合導航系統的量測方程
系統的量測值包含位置和速度的量測值。
位置量測矢量定義如下:
速度量測矢量定義如下:
Hv(t)X(t)+Vv(t)
系統量測方程為:
H(t)X(t)+V(t)
(2)
2 基于神經網絡的GPS/SINS組合導航系統信息融合算法設計
在GPS失鎖時,GPS/SINS組合導航中引入神經網絡信息處理方法,可提高GPS/SINS組合導航系統的精度。
老年重癥肺炎(CAP)是引起老年患者呼吸衰竭的主要原因之一[1],目前,臨床上主要采取機械通氣(MV)等方法支持呼吸。MV是搶救呼吸衰竭患者的重要手段,能夠維持患者的SPO2水平。但治療期間容易引起肺實質感染性炎癥,即呼吸機相關性肺炎(VAP)[2]。VAP是一種嚴重的院內感染,主要發生于機械通氣治療2 d 后及停機撥管后2 d內,不僅會加重患者病情,同時還會嚴重威脅患者生命安全。有報道稱,積極、有效的護理干預能夠提升CAP并發VAP患者的治療效果,改善其預后。因此,本文對老年CAP并發VAP患者加強護理干預,并觀察其對患者治療效果的影響,現報道如下。
2.1 信息融合方法
基于神經網絡的GPS/SINS組合導航系統信息融合方法原理圖,如圖1所示。
(3)
神經元網絡的輸入公式由式(3)決定,由于速度和加速度噪聲的存在,位置差是與速度和加速度有關的非線性函數關系。當GPS信號失鎖時,神經元網絡不再進行訓練,而用它來估計每秒的位置差,對位置差求微分得到速度增量。
GPS位置和速度計算公式如下:
(4)
(5)
式中:Pn、Vn分別為GPS/SINS組合導航系統最后一次融合時的位置和速度。n之后,GPS信號失鎖,神經元網絡開始參與估計飛行器位置,利用此位置信息計算組合濾波器的量測輸入。
2.2 神經網絡模型的推導
如圖1,神經元網絡是組合導航系統的子系統,當GPS信號失鎖時,其每秒估計位置的差。
由式(3)確定的神經網絡輸入節點為6,即東北天3個方向加速度和3個方向速度。理論上講含有一個隱層的網絡,只要隱節點數足夠多,能以任意精度逼近有界區域上的任意連續函數,但以學習時間為代價。輸出層為東北天3個方向位置與上一時刻的位置差值,即神經元個數為3,其網絡模型示意圖如圖2。
在有GPS信號時,卡爾曼濾波器工作在淺組合模式,濾波器每秒鐘輸出一次。GPS/SINS組合濾波結果的當前位置和前一位置的差值作為神經網絡的導師信號。利用慣導得出的3個方向速度和加速度信息作為神經網絡的輸入,對網絡進行訓練。
文中隱層節點激勵函數選為單極性的S型函數,輸出層節點選為線性函數。
設x為輸入信號,其中xi為輸入層神經元i的輸入(i=1,2,…,m);o為隱含層的輸出信號,其中oj為隱含層神經元j的輸出,bj為隱含層神經元j的偏置(j=1,2,…,n);y為輸出層的輸出信號,其中yk為輸出層神經元k的輸出,θk為輸出層神經元k的偏置(k=1,2,…,q);v為隱含層-輸出層權值,其中輸出層的神經元k的權值vk=[vk1,vk2,…,vkn];w為輸入層-隱含層權值,其中隱含層的神經元j的權值wj=[wj1,wj2,…,wjm];η為學習率,d為輸出層的期望輸出(導師信號)。
隱含層中第j個神經元的輸出:
(6)
輸出層中第k個神經元的輸出:
(7)
輸出層權值變化為:
(8)
式中δkj=(dk-yk)f′。

(9)
隱層權值變化為:

(10)
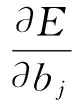
(11)
3 仿真結果與分析
圖3和圖4給出了300 s時間內載體運動的北向速度和加速度曲線,以此作為樣本對神經網絡進行訓練。
仿真軌跡:載體初始位置東經116°,北緯40°,高度7 000 m,初始航向角、俯仰角和橫滾角均為0,初始速度250 m/s,向北飛行。首先平飛40 s,再減速飛行40 s,末速度為150 m/s,航向角變化-8°,俯仰角變化3°,橫滾角不變;然后以150 m/s速度平飛20 s;最后加速飛行40 s,航向角變化8°,俯仰角變化-3°,橫滾角不變,末速度為250 m/s。
誤差條件:陀螺隨機常值漂移為1°/h,陀螺一階馬爾科夫過程噪聲為1°/h,相關時間為100 s。加速度計一階馬爾科夫過程噪聲為0.01g,相關時間為100 s。量測位置白噪聲為15 m,量測速度白噪聲為0.5 m/s,濾波周期1 s。
圖5為神經網絡的訓練過程,設定的網絡誤差為0.05,曲線表明經過200次左右的訓練,網絡的誤差已基本能滿足要求。
圖6和圖7中,給出了GPS/SINS(實線)組合及ANN(虛線)組合導航系統的速度和位置誤差曲線。
由曲線可以看出,在0~50 s兩種組合方式輸出誤差曲線基本一致,50~110 s期間GPS信號失鎖,此時GPS/SINS系統SINS單獨工作,速度和位置誤差呈發散狀態,但有神經網絡參與的ANN組合導航系統誤差未成發散狀態;在110~140 s GPS信號恢復,GPS/SINS系統誤差收斂,ANN與GPS/SINS系統誤差趨勢一致。
4 結論
GPS信號失鎖問題是組合導航系統經常遇到的問題,文中在組合導航系統信息融合算法中引入神經網絡模型,為組合導航系統提供智能支持。神經網絡模擬GPS信息,為組合量測方程提供量測值,改善了在GPS信號失鎖情況下,組合導航系統的導航精度。文中所采用的方法為組合導航系統應用中GPS信號失鎖問題的解決提供了一種方法。
[1] 王惠南. GPS導航原理與應用 [M]. 北京: 科學出版社, 2006: 225-260.
[2] 秦永元. 慣性導航 [M]. 北京: 科學出版社, 2006: 287-360.
[3] CHIANG Kai-Wei,EI-SHEIMY,HUANG Yun-Wen. Huang, An intelligent navigator for seamless INS/GPS intetrated land vehicle navigation applications[J]. Applied Soft Computing,2008,8(1):722-733.
[4] CHIANG Kai-Wei,EI-SHEIMY. INS/GPS integration using neural networks for land vehicular navigation applications[C]//Proceeding of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation. Monassas:ION, 2004:535-544.
[5] 韓力群. 智能控制理論與應用 [M]. 北京: 機械工業出版社, 2008: 96-130.
AlgorithmResearchofGPS/SINSIntegratedSystemBasedonNeuralNetworkDuringGPSOutage
ZHANG Xinmin, ZHANG Wei
(Beijing Aerospace Automatic Control Institute, Beijing 100854, China)
The paper is researched in the problem of GPS information lost in the GPS/SINS integrated navigation system, used the algorithm with neural network. During the outage of GPS, the information of GPS is simulated by the neural network, to supply the measured value to the system and the coupled navigation calculated is going on. The model of integrated navigation system with neural network is given in the paper. The simulation results show that the integrated system with the neural net could insure the precision even the GPS signal lost. The method mentioned in the paper offers a way of solving the problem of GPS signal lost in the integrated navigation system.
integration system; neural network; GPS signal lost
TN967.2
A
2016-06-29
張新民(1984-),男,河北唐山人,工程師,碩士,研究方向:仿真環境模擬。

