一種新的評估末敏彈掃描參數對目標影響模型*

韓廣超, 王 鋒, 趙河明, 張 鋒, 趙歡歡,2

(1 中北大學機電工程學院, 太原 030051; 2 奇瑞新能源汽車技術有限公司, 安徽蕪湖 241000)

一種新的評估末敏彈掃描參數對目標影響模型*

韓廣超1, 王 鋒1, 趙河明1, 張 鋒1, 趙歡歡1,2

(1 中北大學機電工程學院, 太原 030051; 2 奇瑞新能源汽車技術有限公司, 安徽蕪湖 241000)

為了研究末敏彈穩態掃描參數對目標的影響,提出了一種評估末敏彈掃描參數對目標影響的模型。建立了穩態掃描參數影響下的末敏子彈對目標影響模型,并運用MATLAB提供的非線性規劃最優化理論進行了仿真。仿真結果表明:當轉速為5 r/s,落速為9 m/s,掃描角為30°,敏感器探測距離為115～145 m時,末敏子彈最適宜作用目標。所提出的研究思路與方法為末敏彈設計提供一定的幫助,研究內容對分析末敏彈作戰效能具有一定的指導意義。

穩態掃描;MATLAB;非線性規劃最優化;敏感器

0 引言

末敏彈又稱“敏感器引爆彈藥”[1],其利用先進敏感器技術自主搜索、探測、識別目標后,引爆彈藥,形成爆炸成型彈丸(explosively formed projectile,EFP),從頂部攻擊裝甲集群目標。

穩態掃描參數是決定子彈藥系統性能與可靠性高低的關鍵因素,研究末敏彈對目標的作用實際上就是研究穩態掃描參數對目標的影響。文獻[2]提出了子母彈射彈散布模型,仿真目標毀傷效果,從而確定穩態掃描參數。文獻[3]建立了末敏彈命中概率預測模型,運用智能算法對掃描參數進行了優化。文獻[4-5]均是基于正交試驗的靈敏度分析法,確定試驗方案,分析了影響末敏彈對目標攻擊效能的穩態掃描參數。文獻[6]從子彈群落點分布的角度對穩態掃描參數進行了分析。文獻[7-10]通過建立模型,運用算法,對影響末敏彈效能的參數進行了優化。

末敏子彈對目標影響的重要指標是掃描時間、掃描覆蓋面積以及掃描間距[11],而這三項是由穩態掃描參數決定的,因此文中從穩態掃描參數著手,建立末敏彈對裝甲目標影響下的數學模型,運用非線性規劃最優化理論仿真,綜合考慮,最終確定末敏子彈穩態掃描最優參數以及最優參數下的子彈對目標影響。

1 末敏子彈對目標影響因素分析

1.1 末敏子彈工作原理

在穩態掃描階段,子彈體的子彈軸與鉛垂方向成某一角度,通過摩擦盤導旋作用,主旋轉傘帶動子彈體同步旋轉,同時,位于子彈體上的敏感視場在地面以螺旋線的形式由外向內開始對目標進行探測、識別,一旦目標被識別,即刻引爆EFP戰斗部,從頂部攻擊裝甲集群目標。

1.2 末敏子彈對目標影響因素分析

掃描間距與穩態掃描參數之間關系:

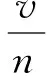
(1)

式中:v為落速;n為轉速。

1)轉速和掃描角一定時,速度越大,掃描間距越大,敏感器捕捉目標幾率減小,子彈對目標影響力降低。

2)轉速和落速一定時,掃描角對子彈作用目標起作用,敏感器探測距離確定時,隨著掃描角增大,掃描間距增大,敏感器捕捉目標幾率減小,影響力下降。

3)落速和掃描角確定時,轉速越大,掃描間距越小,敏感器掃描目標幾率越大,影響力增加。

4)轉速、落速以及掃描角均一定時,敏感器探測距離同樣也會影響子彈對目標影響力。探測距離越大,掃描范圍越大,目標被覆蓋幾率增加,影響力增加。

5)風影響子彈對目標影響力,子彈處于有風環境中,掃描過程中,會使子彈偏離目標群,風速越大,偏離目標群越嚴重,甚至目標脫離掃描覆蓋范圍。

2 末敏子彈對目標影響模型分析與建立

穩態掃描階段,掃描角的選擇一般要考慮子彈的搜索視場和目標背景的輻射反射規律等,通常θ取30°,掃描間距Δ根據敏感器瞬時視場大小,工程上取值一般為1 m≤Δ≤2 m[12]。

設子彈穩態掃描初始高度為H,掃描落線上初始掃描角為A0,初始位置與X軸成α,經時間t后,為掃描螺線上的A1點,則其坐標表示為:

(2)

由式(2)可得出掃描軌跡:

x2+y2=(H-vt)2(tanθ)2

(3)

掃描面積為:

S(t)=π(H-vt)2(tanθ)2

(4)

子彈旋轉一周,下落的距離為:

ΔH=v/n

(5)

考慮末敏彈捕獲準則時,對目標中心區系數選用2/3,文中以敏感器掃過覆蓋面積2/3時發現目標,則子彈對目標影響力定義為該面積與掃描間距的比值,即單位掃描間隔下,敏感器掃過的覆蓋面積的大小,該值越大,目標被探測到的幾率就大,因而子彈對目標的影響力就越大,因此文中所建立的影響力模型為:

(6)

式中a、b、c、d、e、f均為常值。

3 末敏子彈對目標影響仿真分析

a取1 m,b取3 m,c取2 r/s,d取8 r/s,e取5 m/s,f取20 m/s,初始高度H取值范圍70～200 m,利用非線性規劃最優化理論,對影響力進行仿真分析。

3.1 穩態掃描參數最優值分析

根據表1繪制不同探測距離下轉速落速變化趨勢如圖2所示,影響力與探測距離關系如圖3所示。

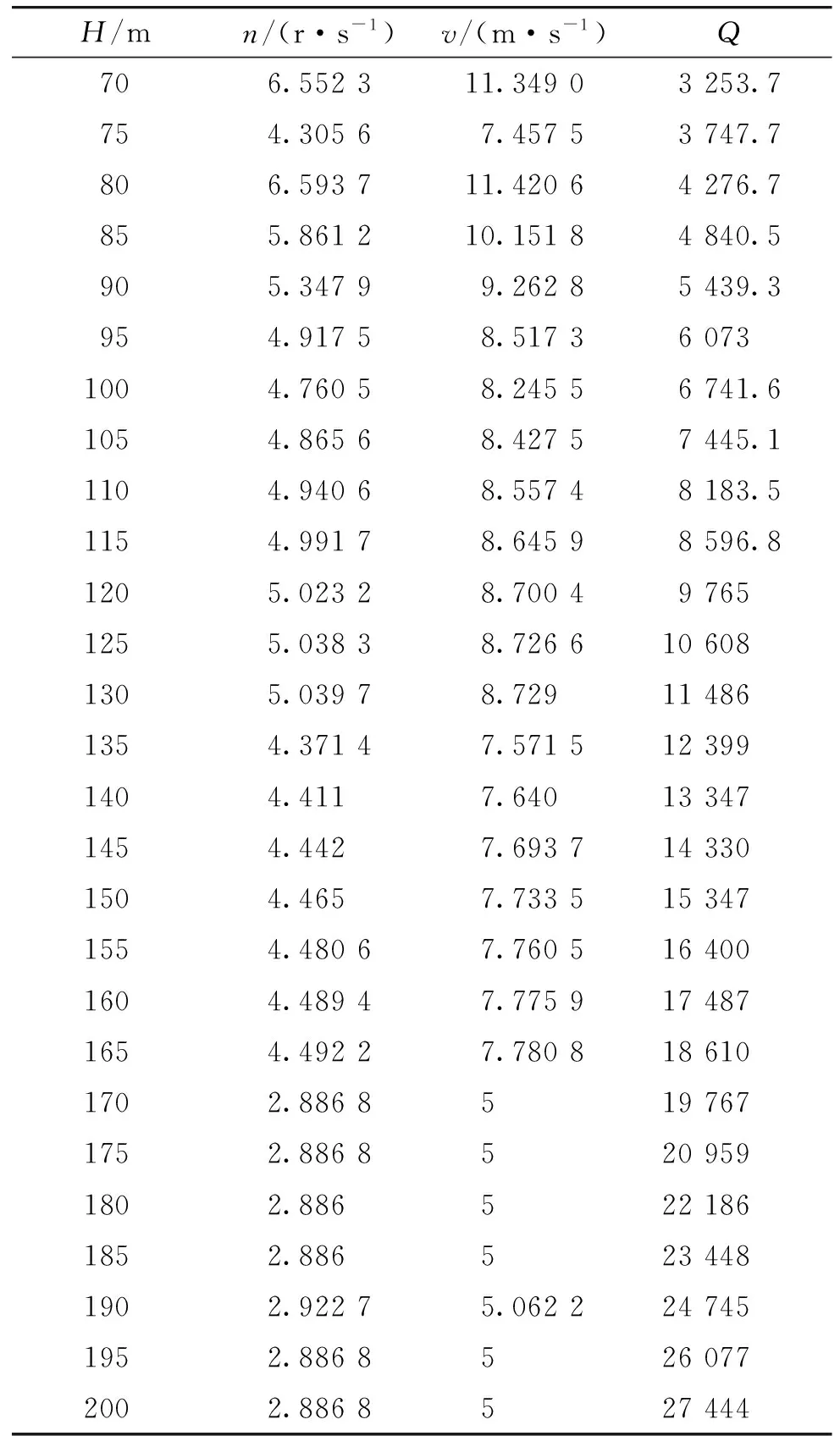
H/mn/(r·s-1)v/(m·s-1)Q706.552311.34903253.7754.30567.45753747.7806.593711.42064276.7855.861210.15184840.5905.34799.26285439.3954.91758.517360731004.76058.24556741.61054.86568.42757445.11104.94068.55748183.51154.99178.64598596.81205.02328.700497651255.03838.7266106081305.03978.729114861354.37147.5715123991404.4117.640133471454.4427.6937143301504.4657.7335153471554.48067.7605164001604.48947.7759174871654.49227.7808186101702.88685197671752.88685209591802.8865221861852.8865234481902.92275.0622247451952.88685260772002.8868527444

從圖2中可看出子彈轉速與落速隨探測距離變化走勢基本一致,在探測距離為80～110 m之間變化波動較大,圖3中可看出該段影響力較小,不易選取;200 m以后均保持不變,轉速約為3 r/s,落速約為5 m/s,經計算掃描間距Δ=0.962 5 m,不滿足工程上掃描間距值,而且隨探測距離增加,雖然掃描覆蓋面積增大,目標落入掃描范圍幾率增加,但由于落速和轉速較小,導致掃描時間長,子彈留空時間長,易被反子彈武器擊毀,因此,本段不可取。探測距離在115～145 m之間與160～190 m之間,轉速落速均變化平穩,115～145 m之間轉速約為5 r/s,落速約為9 m/s,掃描間距Δ=1.039 2 m;160～190 m之間的轉速約為4 r/s,落速約為8 m/s,掃描間距為Δ=1.1570 m,根據圖3在其他參數一定的前提下,探測距離與影響力值成正比,考慮末敏彈滯空以及掃描間距和掃描時間的影響,115～145 m之間的探測距離較為合適。

3.2 優化條件下的各參數值與影響力值的關系

上一小節中,確定轉速、落速一定范圍內的最優值為轉速5 r/s,落速為9 m/s,探測距離最佳范圍115～145 m。以下是各參數值與影響力值的關系。

從圖4、圖5、圖6中可以看出影響力與落速成反比,與探測距離及轉速成正比。落速越快,影響力值越小,影響子彈對目標作用,轉速越高,影響力值越大,探測距離越大,影響力值越大,該仿真結果與1.2節中的分析結果一致。

3.3 風對末敏子彈影響力的影響

圖7、圖8、圖9(紅色代表目標)對比分析可知:當末敏子彈處于無風作用下時,目標均位于探測器掃描覆蓋面內,影響力值最大,當vx=vz=2 m/s時,如圖8所示,目標也均處于探測器掃描覆蓋范圍內,但相對無風情況下,其影響力降低;圖9中在vx=2 m/s,vz=2.5 m/s,有一部分目標脫離探測器掃描范圍,如果風速更大的話,所有目標均會脫離掃描范圍,這時末敏彈就對目標失去了作用。該仿真結果也與1.2節中的定性分析較為一致。

4 結論

文中從末敏彈穩態掃描階段的轉速、落速、掃描角以及敏感器的探測距離等參數角度出發,建立了末敏子彈對目標影響作用的數學模型,運用非線性規劃最優化理論仿真,確定了最佳穩態掃描參數及其影響力,仿真結果與定性分析相一致,證明了所建立的模型的正確性。通過文中所建立的模型,可以確定某一轉速范圍、落速范圍以及探測距離范圍下的最優穩態掃描參數以及子彈對目標的影響力值,文中的研究內容對分析末敏彈的作戰效能具有一定的指導意義,同時,文中所提出的研究方法、思路和分析方法也為末敏彈的整體設計提供了一定幫助,具有一定的實際應用意義。

[1] 高曉敏. 新概念信息化彈藥的現狀與發展 [J]. 四川兵工學報, 2008, 29(4): 69-73.

[2] 李秀亮, 張成禮, 王德群, 等. 子母彈射彈散布仿真及其設計效率計算 [J]. 計算機仿真, 2010, 27(1): 9-12.

[3] 唐克, 王存威. 末敏彈命中概率預測模型研究 [J]. 艦船電子工程, 2011, 31(3): 119-121.

[4] 黃鹍, 劉榮忠. 末敏彈系統效能靈敏度分析 [J]. 兵工學報, 2001, 22(3): 412-415.

[5] 黃鹍, 劉榮忠. 末敏彈性能影響因素靈敏度分析 [J]. 彈道學報, 2001, 13(1): 21-26.

[6] 孔維紅, 姜春蘭, 王在成. 某型航空子母彈子彈地面散布研究 [J]. 航空兵器, 2005(4): 43-46.

[7] 張靜, 郝慶麗. 基于混沌退火算法和BPNN模型的末敏彈系統效能參數優化 [J]. 武器裝備自動化, 2006, 25(4): 15-16.

[8] 黃風華, 劉榮忠, 郭銳. 基于混合神經網絡的末敏彈系統參數優化設計 [J]. 計算機仿真, 2012, 29(3): 53-56.

[9] 唐克, 王存威, 盧金星. 基于神經網絡和MATLAB的末敏彈系統效能靈敏度仿真 [J]. 兵工自動化, 2010, 29(7): 90-93.

[10] 姜禮平, 張緒春, 王平. 基于支持向量機和遺傳算法的末敏彈系統效能參數優化設計 [J]. 海軍工程大學學報, 2007, 19(1): 32-34.

[11] 楊啟仁. 子母彈飛行動力學 [M]. 北京: 國防工業出版社, 1999: 265-287.

[12] 楊紹卿. 靈巧彈藥工程 [M]. 北京: 國防工業出版社, 2010: 33-35.

ANewModelofAssessingtheInfluenceofTerminal-sensitivityProjectileSteadyStateParametersAgainstTargets

HAN Guangchao1, WANG Feng1, ZHAO Heming1, ZHANG Feng1, ZHAO Huanhuan1,2

(1 School of Mechatronics Engineering, North University of China, Taiyuan 030051, China; 2 Chery New Energy Automotive Technology Co. Ltd, Anhui Wuhu 241000, China)

In order to study how Terminal-sensitivity Projectile (TSP) steady state scanning parameters affected targets, a model of assessing the influence of TSP scanning parameters against targets was proposed in the paper. The influence model of submunitions against targets was established, which was in the influence of steady state scanning parameters, and the simulation was carried out by non-linear programming optimization theory provided by MATLAB. The simulation results show that:under the circumstances of the scanning angle is 30° and sensor detection is 115～145 m, when the speed is 5 r/s and off-speed is 9 m/s, the submunition is against targets at best. research ideas and methods provide some help of TSP design, and research contents have certain significance for TSP operational effectiveness.

stead state scanning; MATLAB; non-linear programming optimization; sensor

TJ410.1;TP391.9

A

2016-03-21

國防科工局技術基礎項目資助

韓廣超(1989-),男,山東濟寧人,碩士研究生,研究方向:智能彈藥。