非高斯噪聲環境中基于梯度范數的自適應濾波算法*

馮子昂, 胡國平, 匡旭斌, 周 豪

(1 空軍工程大學防空反導學院, 西安 710051; 2 93861部隊, 陜西三原 710000)

非高斯噪聲環境中基于梯度范數的自適應濾波算法*

馮子昂1, 胡國平1, 匡旭斌2, 周 豪1

(1 空軍工程大學防空反導學院, 西安 710051; 2 93861部隊, 陜西三原 710000)

針對傳統最小均方類算法在非高斯噪聲中自適應濾波性能下降的問題,提出了一種基于梯度范數的變步長歸一化最小平均p范數算法。算法將α穩定分布作為非高斯噪聲分布模型,依靠梯度范數與均方權值偏差(MSD)的關系自適應調整步長,加快收斂速度的同時減小穩態誤差,理論推導證明了算法的有效性。仿真結果表明,在非高斯噪聲條件下,該算法具有更好的收斂性能和抗突變能力以及更小的穩定誤差。

α穩定分布;自適應濾波;梯度范數;歸一化最小平均p范數算法

0 引言

在傳統的信號處理領域中,基于高斯分布的白噪聲模型廣泛應用于接收機的設計之中。在理想的高斯白噪聲假設下通常可以得到信號處理問題的閉式最優解,從而能夠降低信號處理算法和接收機結構設計的復雜程度[1]。但是在實際問題中,具有明顯的尖峰脈沖和長拖尾特性非高斯信號和噪聲廣泛存在,如低空環境下的雜波、大氣噪聲以及海洋噪聲等。在這種噪聲條件下,基于高斯假定下的信號處理算法的性能將會急劇下降甚至失效。α穩定分布作為唯一一類滿足中心極限定理的分布,能夠描述多個獨立同分布隨機變量之和的極限分布[2-3],又有實測數據作支撐,在描述具有尖峰脈沖特性的非高斯信號時具有廣泛的適用性。

基于高斯假定的時域自適應濾波系統中常用的算法是基于最小均方誤差(minimum mean square error,MMSE)準則的最小均方(LMS)類算法和遞歸最小二乘(RLS)類算法。由于α穩定分布不存在二階及二階以上矩,因此以上兩種算法在α穩定分布噪聲環境中無法發揮出最佳性能。針對這一問題,Shao和Nikias在最小分散系數(minimum dispersion,MD)準則的基礎上率先提出了最小平均p范數(LMP)算法[4-5];Belge和Miller受RLS算法的啟發,提出了利用加權最小二乘的RLP算法[6]。為了兼顧收斂速度和穩態誤差,人們對變步長LMS算法進行推廣[7-12],文獻[13]提出了一種變步長LMP算法,提高了算法的性能,但是該算法需要已知信噪比這一條件,在實際應用中仍存在諸多困難。因此文中在眾多變步長NLMS算法的基礎上,借鑒Shin提出的最優化變步長LMS算法[9]的思想,研究了一種變步長LMP算法,算法利用梯度范數與均方權值偏差之間的關系,實現梯度范數對迭代步長的控制,并分析證明了算法的穩定收斂性。最后利用仿真驗證了算法的相關性能。

1 非高斯α穩定分布噪聲模型

Levy在研究廣義中心極限定理時提出了α穩定分布,該分布的概率密度函數無閉式解,通常用特征函數來描述其分布特征[1]。α穩定分布的特征函數可表示為:

φ(t)=E{exp(jtx)}=

exp{jδt-γ|t|α[1+jβsgn(t)ω(t,α)]}

(1)

式中:

(2)

(3)

其中:

1)α∈(0,2]為特征指數,與分布的拖尾厚度緊密相關。當α的值越小時,分布的拖尾越厚,非高斯特性也就越明顯。

2)β∈[-1,1]代表偏斜參數,用來描述分布的對稱特性,β=0時的分布被稱作對稱α穩定分布,即SαS。

3)γ>0代表分散系數,用來描述分散程度。

4)δ∈(-∞,∞)對應于分布位置參數,對于SαS,δ表示分布的均值(1<δ≤2)或中值(0<δ≤1)。

由此可見,α穩定分布具有的4個參數即可確定一個穩定分布的特征函數,改變不同的分布參數幾乎可以描述所有的噪聲統計特征,十分靈活,因此作為非高斯噪聲模型具有廣泛的適用性。同時α穩定分布存在幾種特殊形式[14],即α=2時的高斯分布及α=1,β=0時的柯西分布和α=0.5,β=-1時的Levy分布。

2 基于梯度范數的變步長NLMP算法

2.1NLMP算法

對于一個M階FIR自適應濾波器,濾波器在k時刻的輸出為:

(4)

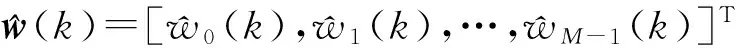
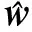
(5)

式中:d(k)=xT(k)wopt(k)+v(k)是期望響應,wopt(k)是最優權系數,v(k)是服從α穩定分布的噪聲。

由分數低階矩理論可知,對于任意的1≤p<α,服從SαS分布的隨機變量的分數低階矩與其p范數成正比,且其所有分數低階矩都是等價的,那么該自適應濾波器的代價函數可表示為:

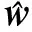
(6)

用誤差的統計平均代替瞬時值,并對代價函數求偏導,得到代價函數的瞬時梯度估計值:

-p|e(k)|p-1sign(e(k))[x(k)]

(7)

因此可知算法的權系數更新方程為:

(8)

式中：μ>0,1≤p<α。μ為步長,控制收斂速度和穩態誤差。根據NLMS算法的思想,在式(7)中對瞬時梯度進行歸一化,則可得到NLMP算法的權系數更新公式為:

(9)

式中：λ為一適當的小正數,用來避免分母為零的情況。NLMP算法有效改善了LMP算法中存在的梯度噪聲放大的缺點,提高了算法的收斂速度和穩定性,同時從式(9)可以看出,當p=2時,NLMP算法就會退化為NLMS算法,因此具有廣泛的適用性。

2.2 改進的變步長NLMP算法

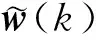
文中利用梯度矢量與MSD之間的聯系,提出了一種基于梯度范數的變步長NLMP算法,首先對梯度矢量進行平滑,然后利用平滑梯度矢量的歐氏范數控制迭代步長,在迭代的初始階段,較大的均方誤差使得步長相對較大,算法的收斂速度也相對較快;當自適應濾波器的權系數接近最優值時,系統收斂,迭代步長隨著均方誤差逐漸減小,進而降低了穩態誤差,提高了系統的穩定性。

算法的步長和權值更新公式如下:

(10)

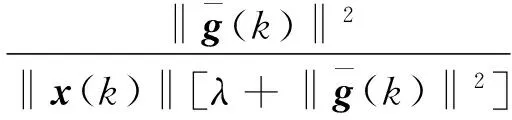
(11)

(12)

3 穩定性分析

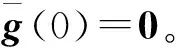
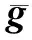
(13)

則該平滑梯度向量歐氏范數平方的期望為:

(14)

(15)

將式(15)代回式(14),則有:

(16)

在式(16)中,假設i≥K時,系統達到穩定狀態,式中忽略K之前的項是因為此時這些項的值趨近于零。

對式(12)進行如下處理:

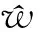
(17)

式中：令

當i≥K時系統達到穩定狀態。由于1≤p<α<2,所以對于有限功率的輸入信號x(k),都有E{‖x(k)‖2|e(k)|2(p-1)}<∞,因此文中提出的算法在非高斯α穩定分布噪聲條件下是可以收斂的。

4 仿真分析

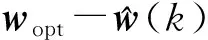
仿真一 特征指數α對算法收斂性的影響

由于α穩定分布不具有2階以上的高階矩,因此α穩定分布不具有功率的概念。此時的廣義信噪比可表示為:

(18)

仿真二 弱噪聲環境下算法收斂性

設定廣義信噪比GSNR=20 dB以模擬弱噪聲環境。算法參數ρ、μmax、λ的設置與仿真一相同。非高斯噪聲的特征參數α=1.5。將Shin算法作為與文中算法進行對比的變步長LMS算法,其參數設置同上所述,這種設置可以使Shin算法的性能達到最佳[16]。文中算法和Shin算法的初始步長均為0。圖3給出了弱噪聲環境下權系數誤差與迭代次數的關系曲線。從圖中可以看出,相較于Shin算法和固定步長的NLMP算法,文中提出的VSS-NLMP算法在初始階段具有最快的反應速度,并且在迅速達到了穩態的同時顯著降低了系統的穩態誤差。

仿真三 強噪聲環境下算法收斂性

設定廣義信噪比GSNR=0 dB以模擬強噪聲環境。算法參數設置為ρ=0.99,μmax=0.05,λ=1,初始步長為0。非高斯噪聲的特征參數α=1.5。Shin算法的參數設置與上述相同。從圖4中可得到強噪聲環境下權系數誤差與迭代次數的關系曲線。雖然穩態誤差較弱噪聲環境中有所增大,但是VSS-NLMP算法依然比其他兩種算法具有更快的反應速度,能夠迅速達到穩態并較好的降低了穩態誤差。由此可以看出,文中提出的算法強噪聲和弱噪聲環境中都有較好的性能。

仿真四 系統突變時算法收斂性

設定廣義信噪比GSNR=20 dB,其他參數設置與仿真二相同。假設當迭代次數為2 500時,系統參數發生一次突變,之后恢復正常。圖5為權系數誤差在突變前后的收斂曲線。由以上圖可以看出,盡管在迭代過程中系統參數發生了突變,相較于其他兩種算法,本算法依然能夠迅速反應并在短時間內恢復收斂,具有良好的抗突變性能。

5 結語

服從α穩定分布的非高斯噪聲廣泛存在于工程實踐之中,而傳統LMS類自適應濾波算法在這類噪聲環境中性能會發生退化。文中提出了一種基于梯度范數的變步長歸一化LMP算法,該算法利用梯度范數與MSD之間的關系自適應的調整迭代步長。最后通過仿真考察了非高斯噪聲特征指數α對算法性能的影響,比較了文中算法和Shin算法、NLMP算法在強、弱噪聲環境的性能,仿真結果顯示在非高斯α穩定分布環境中所提算法不僅提升了收斂速度還降低了穩態誤差,使得算法性能得到了較大提高,并且在抗系統突變方面也有良好的表現。這種算法在通信、雷達信號處理等領域有著良好的應用前景。

[1] CHRYSOSTOMOS L. Signal processing with Alpha-stable distributions and applications [M]. New York: John Wiley & Sons Inc., 1995.

[2] TSIHRINTZIS G A, NIKIAS C L. Evaluation of fractional lower-order statistics-based detection algorithms on real radar sea-clutter data [J]. IEE Proceedings, Radar, Sonar and Navigation, 1997, 144(1): 29-38.

[3] 郭瑩. 穩定分布環境下的時延估計新方法研究 [D]. 大連: 大連理工大學, 2009.

[4] SHAO M, NIKIAS C L. Signal processing with fractional lower order moments: Stable processes and their application [J]. Proceedings of the IEEE, 1993, 81(7): 986-1010.

[5] ARIKAN O, BELGE M, CETIN A E, et al. Adaptive filtering approaches for non-gaussian stable processes [C]// IEEE International Conference on Acoustics, Speech, and Signal Processing. Detroit，MI，USA， 1995: 1400-1403.

[6] BELGE M, MILLER E L. A Sliding Window RLS-like Adaptive Algorithm for Filtering Alpha-stable Noise [J]. IEEE Signal Processing Letters, 2000, 7(4): 86-89.

[7] ANG W P, FARHANG-BOUROUJENY B. A New class of gradient adaptive step-size LMS algorithm [J]. IEEE Transactions on Signal Processing, 2001, 49(4): 805-810.

[8] 高鷹, 謝勝利. 一種基于相關函數的LMS算法 [J]. 數據采集與處理, 2004, 19(1): 1-4.

[9] SHIN H C, SAYED A H, SONG W J. Variable step-size NLMS and affine projection algorithms [J]. IEEE Signal Processing Letters, 2004, 11(2): 132-135.

[10] LU L, ZHAO H Q. Combination of two NLMP algorithm for non-linear system identification in Alpha-stable noise [C]// IEEE China Summit & Int Conf on Signal and Information Processing. Chengdu, 2015: 1012-1016.

[11] NAVIA-VAZQUEZ A, ARENAS-GARCIA J. Combination of recursive least P-norm algorithm for robust adaptive filtering in Alpha-stable noise [J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1478-1482.

[12] LU L, ZHAO H Q. A Novel convex combination of LMS adaptive filter for system identification [C]// International Conference on Signal Processing(ICSP). [S.l.:s.n.], 2015: 225-229.

[13] 張莉, 馮大政. 一種改進的自適應脈沖對消LMP算法 [J]. 西安電子科技大學學報, 2003, 30(2): 183-185.

[14] 康亞明, 曹保衛. Alpha穩定分布隨機變量仿真及模型參數估計 [J]. 電子設計工程, 2011, 19(11): 19-22.

[15] 單志明.α穩定分布參數估計及自適應濾波算法研究 [D]. 哈爾濱: 哈爾濱工程大學, 2012.

[16] 李寧, 張勇剛, 郝燕玲. 一種魯棒性變步長LMS公式的穩態性能分析 [J]. 系統仿真學報, 2008, 20(18): 4978-4981.

AnAdaptiveFilteringAlgorithmBasedonGradient-norminNon-GaussianEnvironment

FENG Ziang1, HU Guoping1, KUANG Xubin2, ZHOU Hao1

(1 Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China; 2 No.93861 Unit, Shaanxi Sanyuan 710000, China)

Conventional least mean square(LMS) algorithms meet declines of performance in non-Gaussian environment. A new variable step-size normalized least mean p-norm algorithm based on gradient-norm is proposed. The new algorithm assumes that the non-Gaussian noise satisfies alpha stable distribution, and the step size is adaptively adjusted by the relationship between mean square departure (MSD) and the gradient-norm. Through the relationship, the convergence rate is accelerated and the steady state error is decreased at the same time. The performance of the proposed algorithm is confirmed by theoretical derivation. Simulation results show that the proposed method has faster convergence rate, smaller steady state error and better performance of anti-saltation in non-Gaussian environment.

α-stable distribution; adaptive filtering; gradient norm; normalized least meanp-normalgorithm

TN911.72

A

2016-05-20

國家自然科學基金(61372166);陜西省自然科學基礎研究計劃(2014JM8308)資助

馮子昂(1993-),男,山東濟寧人,碩士研究生,研究方向:雷達信號與信息處理。