告訴你“代數式”背后的故事
曹 燕
告訴你“代數式”背后的故事
曹 燕
如果我問你,在這個世界上,你最熟悉的人是誰,你肯定會告訴我,當然是媽媽,其次是爸爸.可為什么媽媽是你最熟悉的那個人呢?可能你會說出很多的理由.但根本原因是,人們在認識人物和事物的時候,總是從最特殊的開始,而媽媽就是你最特殊的那一個,在認識特殊的基礎上再逐步認識一般的.在數學的學習過程中,同樣如此.從特殊到一般是認識事物的一般規律,在數學上稱之為歸納.“代數式”的內容作為數學中非常重要的知識,我們也要遵循“從特殊到一般,再從一般回到特殊”的規律來認識它.
一、從特殊到一般
我們在第二章學習的有理數,屬于“數”的范疇,接著學習的第三章代數式,屬于“式”的范疇,從數到式就是“從特殊到一般”規律的體現.
小學里我們已經學習了三角形的面積公式,三角形的面積等于底乘以高除以2.所以,你只要告訴我一個三角形的底是多少,高是多少,我就可以利用上面的公式計算出此三角形的面積.如一個三角形的底為5,高為4,那么這個三角形的面積為×5×4=10.顯然,三角形有無數個,每次都要根據不同的底與高進行不同的計算表達,不是我們數學所希望出現的和追求的.因為數學講究的是最優、最簡、最美.此時,字母代替數,也就是我們所說的代數式“粉墨登場”了,不同三角形的底的長度是一個具體的數,我們可以用一個一般的字母a來表示,不同三角形的高的長度是一個具體的數,我們可以用一個一般的字母h來表示,于是三角形的面積就等于ah,這個代數式就可以代表所有三角形的值,如果用S來表示三角形的面積,那么S=ah就是所有三角形的面積計算公式.可見字母表示數,是用一個代數式代替無數個具體的數的計算式子,從特殊走向一般,簡潔明了,作用非常巨大.
在有理數的學習中,我們需要驗證小學里算術中學習的加法交換律、加法結合律、乘法交換律、乘法結合律、乘法對加法的分配律對有理數是否仍然適用,你還記得是如何驗證的嗎?如有理數范圍內加法的交換律,我們是通過5+3=?,3+5=?,5+(-3)=?,(-3)+5=?,(-5)+3=?,3+(-5)=?,(-5)+(-3)=?,(-3)+(-5)=?這幾組特殊的算式逐一進行計算,發現兩種不同的算法得到的結果5+3=3+5,5+(-3)=(-3)+5,(-5)+3=3+(-5),(-5)+(-3)=(-3)+(-5)是一樣的,通過從特殊到一般的歸納,我們就得到了加法交換律a+b=b+a.其他的運算律也用相同的方法獲得.
可見,從特殊到一般不僅是日常生活中認識事物的一般規律,同樣是數學學習中認識數學的一般規律,這種方法需要同學們引起高度的重視.在今后的數學學習過程中,當你研究了一些特殊的問題之后,不妨想想能不能把這個特殊情況推廣到一般的情形,這叫特殊問題一般化.從上面的研究我們可以看出,從特殊走向一般是一次質的飛越,許多規律和發明創造就孕育其中.
二、從一般回到特殊
如果說用字母表示數產生代數式是從特殊的數到一般的式的飛躍,那么,從代數式到代數式的值就是從一般再回到特殊.
例 已知,用下圖中所示的字母表示陰影部分的面積為 .
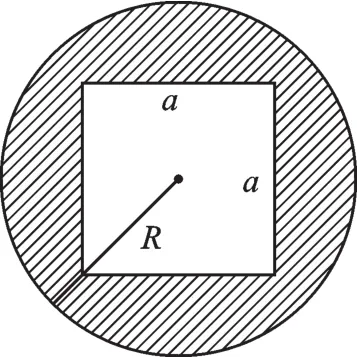
若R=5cm,a=3cm,則圖中的陰影部分的面積為 (其中π取3.14).
解析:圖形由正方形與圓組成,圓半徑為R,正方形邊長為a,已經完成了用一般字母表示具體數的飛躍,所以,第一個問題就可以直接用一般的代數式表示出陰影部分的面積為πR2-a2.很顯然,由于半徑用R來表示,是不確定的值,滿足圓半徑R的值有無數個;同樣,邊長用a來表示,也是不確定的值,滿足正方形邊長a的值也有無數個,代數式πR2-a2表示的就是一個大圓中挖去一個小正方形余下的陰影部分的面積.而下一個問題告訴我們,R=5,a=3,都是具體特殊的數,說明圓的大小與正方形的大小都是唯一確定的,此時要求陰影部分的面積,實際上就是求當R=5,a=3時,代數式πR2-a2的值,只要把R=5,a=3代入代數式,就可以求出其值為69.5.從上面的分析過程可以看出,當代數式中字母的具體數值確定的時候,求代數式的值本質上就是用具體的數代替代數式中的字母,進而變成數的計算問題,這樣,式的問題又回到了數的問題.可見,求代數式的值實際上就是從一般回到特殊.通過字母表示數產生代數式,從特殊到一般,當字母的值確定后,從代數式回到代數式的值,又從一般到特殊,正好完成了“特殊——一般——特殊”的循環.
在今后的學習數學過程中,當你遇到要研究一個一般的問題,你又無法解決時,不妨先從特殊的情況入手進行嘗試,從一般回到特殊,也叫一般問題特殊化考慮,相信你會有更大的收獲.
最后需要告訴同學們的是:“從特殊到一般,從一般到特殊”是認識生活問題、認識數學問題非常重要的一種方法.初中階段我們的數學學習才剛剛開始,在今后的學習中,同學們一定要牢記這種方法,并在認識數學、解決問題的過程中不斷去嘗試和掌握,相信這種方法會讓你終身受益!
(作者單位:江蘇省宜興市陶都中學)

