考慮裕量損失函數的預測控制新架構

周衍彤 羅雄麟 許 鋒

(中國石油大學(北京)地球物理與信息工程學院)

考慮裕量損失函數的預測控制新架構

周衍彤 羅雄麟 許 鋒

(中國石油大學(北京)地球物理與信息工程學院)

在常規預測控制性能指標函數的基礎上加入一個表征操作變量空間變化情況的裕量損失函數，提出一種考慮裕量損失函數的預測控制新架構，并推導其優化求解過程。同時，通過穩態最優值分析新架構保留操作變量空間的效果，并采用穩態分析在預測控制中加入裕量損失函數對控制效果的影響。最后，通過實例仿真證實了新算法的有效性。

連續攪拌反應器 模型預測控制 裕量損失函數

由于實際的化工過程系統存在慢時變、大滯后、干擾及周期性等不確定因素[1]，為保障系統的實際應用與安全性，工藝人員在長周期工藝設計初期通常為變量預留了一定的裕量。在動態操作優化過程中，操作控制會消耗操作變量的可操作空間[2，3]，雖然工藝人員已經為操作變量設計了裕量，但是控制人員在進行操作時希望令單次控制中操作變量消耗的空間盡可能地少，不僅可以為長周期過程工藝內以后的控制留下更多的操作空間和余地，將控制的“好處”緩慢地釋放，而且可以將操作點控制在工藝裕量限以下，保障生產可靠和安全。預測控制由于其區間控制[4，5]和多變量控制的特點，可以實現在工藝生產操作優化的動態控制過程中減少操作變量的空間損耗。為此，提出一種在常規預測控制性能指標函數中考慮裕量損失函數的預測控制新架構。國內外學者針對預測控制做了大量的研究，有許多通過改進預測控制性能指標函數以改進預測控制性能的研究成果。文獻[6，7]和文獻[8]分別提出在預測控制的性能指標中引入終端約束來保證預測控制系統的穩定性；文獻[9]在常規預測控制性能指標中加入靜態目標，在滿足基本控制要求的基礎上進一步實現系統的經濟指標等。

對預測控制中的裕量研究，文獻[10]通過在長周期化工過程的動態優化中采用預測控制，為設計變量進行裕量設計；文獻[11]研究了先進控制條件下化工過程的操作裕量和控制系統性能之間的關系。上述在預測控制中討論的裕量，都是研究長周期過程工藝通過動態優化進行裕量設計的。

為了說明在預測控制中考慮裕量損失函數的正確性與科學性，筆者對在預測控制中考慮裕量損失函數的方法論的產生、存在意義及其必然性[12]進行深入剖析。從實際應用角度，深入探討考慮裕量損失函數的預測控制與常規預測控制相比節省操作變量空間的效果，并分析為了在控制中少消耗操作變量的空間對控制帶來的影響。筆者研究了所提方法在預測控制的短周期動態過程中考慮操作裕量的變化情況。

1 裕量損失函數

在化工過程中，對于存在約束的系統，為避免在邊界操作點由裝置和工藝本身的不確定因素帶來的約束破壞性，將操作點移到約束邊界內，移動后的操作點與約束邊界之間的距離即為裕量[13]。要想實現在單次控制中令操作變量消耗的空間盡可能地少，需要定性表征操作變量消耗空間的情況，為此引入操作裕量的概念。根據裕量的定義，將操作裕量定義為操作變量的操作點與約束邊界之間的距離(圖1)。當操作變量的操作點與約束邊界之間的距離減小時，操作裕量減小，過程可操作空間減少，控制消耗的裕量越多；當操作變量的操作點與約束邊界之間的距離增大時，操作裕量增大，過程可操作空間增大，控制消耗的裕量越少。

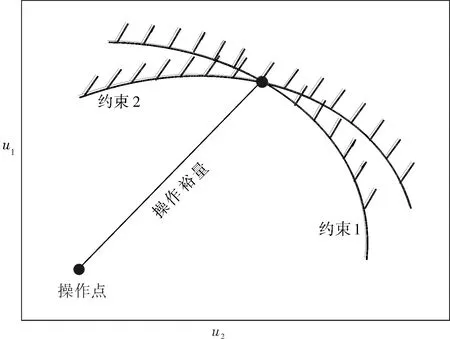
圖1 操作裕量示意圖

為定量考慮動態控制中操作裕量的變化情況，構建一個表示操作變量操作點u與約束邊界之間距離的函數，并定義為裕量損失函數。二范數是具有“長度”概念的函數，通常用來表示兩點或向量矩陣之間的直線距離，因此裕量損失函數fML的數學表達式記為：

fML=‖u-uH‖2

式中uH——操作變量的約束上界。

2 考慮裕量損失函數的預測控制

2.1 新架構

常規預測控制是一種基于優化的控制算法，它通過某一性能指標的最優來確定未來的控制作用[14]，為了在預測控制的動態過程中實現增大操作裕量并減少控制消耗裕量，在性能指標中加入裕量損失函數改進常規預測控制的結構，最終將優化問題轉換為二次規劃進行求解。

常規預測控制的性能指標函數通常可以寫成二范數的形式：

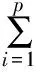
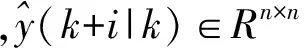
優化求解預測控制的性能指標函數，轉換為二次規劃的標準形式后，成為求目標函數的極小值，所以在預測控制中引入的裕量損失函數fML_MPC記為負值形式：

fML_MPC=-‖u-uH‖2

因此，考慮裕量損失函數的預測控制的優化性能指標為：

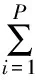
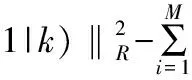
(1)

其中，S≥0為裕量損失函數的權重。

自此，提出考慮裕量損失函數的預測控制(Model Predictive Control with Margin Loss，MLMPC)新架構。

2.2 優化求解過程

假定預測控制采用的線性時不變離散狀態空間模型增量化之后的形式如下：

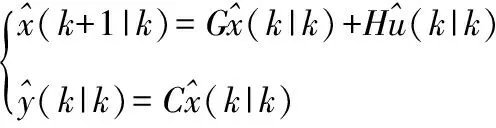
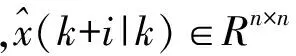
假設系統狀態可測，采用矩陣和向量形式表示對輸出的預測，即：

(2)

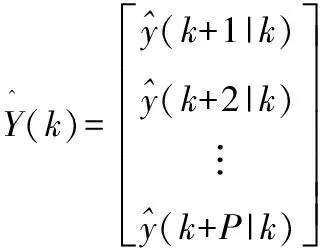
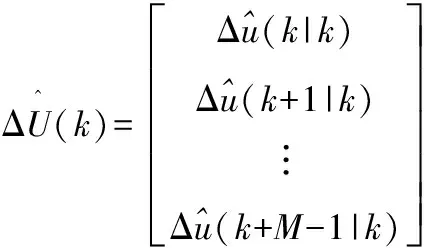
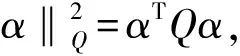
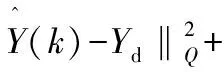
(3)

考慮系統關于輸入、輸入變化量和輸出的約束：

umin≤u(k)≤Δumax

Δumin≤Δu(k)≤Δumax

ymin≤y(k)≤ymax

則前述考慮裕量損失函數的預測控制優化問題可最終表述為如下標準二次規劃形式：

Ψ=2?SΔUTQSΔU+R-ETSE」

Θ=2{-[Yd-Y0(k)]TQSΔU-U1TSE}

d1=[umax-u(k-1),umax-u(k-1),…,umax-u(k-1),-umin+u(k-1),-umin+u(k-1),…,-umin+u(k-1)]T

d2=[Δumax,…,Δumax,-Δumin,…,-Δumin]T

d3=[ymax-y0(k+1),…,ymax-y0(k+P),-ymin+y0(k+1),…,-ymin+y0(k+P)]T

3 控制效果分析

引入常規預測控制的優化問題(4)，通過優化求解式(4)可以得到常規預測控制的最優解：

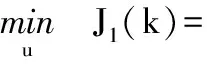
s.t.u=G-1y

(4)

Su≤T

式中G——穩態增益矩陣；

S、T——約束系數矩陣。

同理，求解式(5)可以得到與常規預測控制參數相同的考慮裕量損失函數的預測控制的最優解：

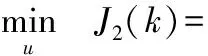
s.t. u=G-1y

(5)

Su≤T

那么有定理1存在。

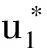
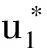
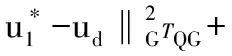
(6)

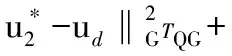
(7)

式(6)和式(7)相加可得：

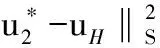
(8)

定理1得證。

4 考慮裕量損失函數的預測控制對控制效果的影響分析

考慮裕量損失函數的預測控制可以在控制的動態過程中實時增大操作裕量，減少單次控制中操作變量消耗的空間，但是與此同時會對被控變量跟蹤給定值造成一定的影響。為定量探討考慮裕量損失函數的預測控制對控制效果的影響，需對考慮裕量損失函數預測控制的穩態情況進行分析。但是，對于存在約束的系統，由于約束的存在難以求解解析解，導致針對控制系統進行穩態分析比較困難。然而，對于同一個控制系統，在無約束情況下的穩定性是在相同控制參數下有約束控制系統穩定的必要條件[15]。同時，在存在約束的預測控制中考慮裕量，通常都會使過程在約束可行域內運行。因此，為了分析考慮裕量損失函數預測控制的穩態情況，可以分析在無約束條件下控制系統的閉環特性，將得到的最優控制作用帶入閉環方程中，并判斷穩態解的情況。

當被控過程的離散狀態空間模型為：

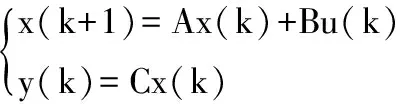
(9)

其中，系統狀態變量x(k)∈Rn×n，系統輸入變量u(k)∈Rm×m，系統輸出變量y(k)∈Rr×r；系統狀態矩陣A∈Rn×n、輸入矩陣B∈Rn×m、輸出矩陣C∈Rr×m。

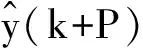
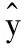
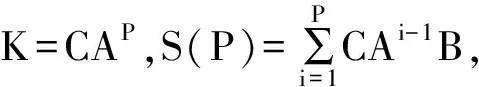
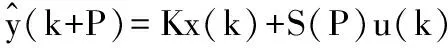
(10)

為了便于分析最終輸出達到穩態的跟蹤效果，將裕量損失函數用輸出形式表示為：

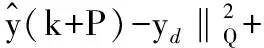
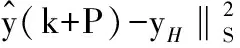
(11)

其中，yH為操作變量約束上界對應的輸出變量的值，S′為輸出對應的裕量損失函數的權重。由于Δu(k)=u(k)-u(k-1)，將式(10)代入式(11)，有：

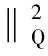
=const+uT(k)ST(P)QS(P)u(k)+2uT(k)ST(QP)Kx(k)-yd)+uT(k)Ru(k)-

2uT(k)Ru(k-1)-uT(k)ST(P)S′S(P)u(k)-2uT(k)ST(P)S′(Kx(k)-yH)

則有：

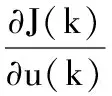
2ST(P)S′(Kx(k)-yH)=0

得到控制最優值，并進行z變換可得：

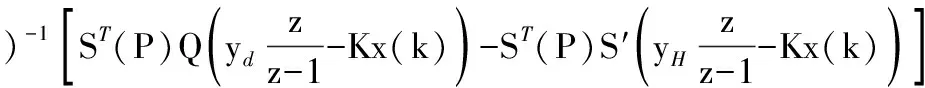
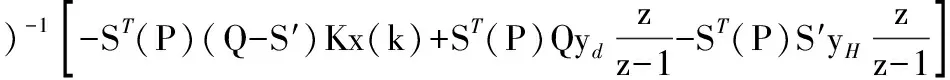
(12)

假設實際過程也遵循式(9)，則對式(9)做z變換，有：

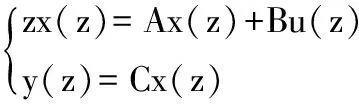
(13)

將式(12)代入式(13)，可得：

y(z)=C[zI-A+B(ST(P)QS(P)+R-Rz-1-ST(P)S′S(P))-1ST(P)(Q-S′)K]-1·

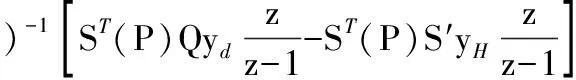
(14)

為判斷穩態情況，對式(14)使用終值定理并進行推導：

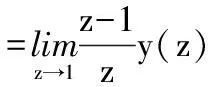
=C[I-A+B(ST(P)QS(P)-ST(P)S′S(P))-1(ST(P)(Q-S′)K]-1·

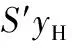
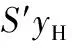
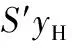
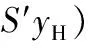
(15)

其中，Gm(z)表示模型的傳遞函數，則有C(I-A)-1B=Gm(1)。由式(15)可得：

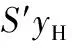
(16)

矩陣(Q-S′)非奇異是輸出變量存在穩態解的必要條件。由式(16)可以看出，輸出變量的穩態值為輸出期望值yd與工藝裕量值yH之間的函數。因此，在考慮裕量損失函數的預測控制中，當權重Q和S′都不趨近于零時，輸出的穩態值為輸出期望值與操作變量約束上界對應的輸出變量的值之間的函數，不能準確無誤地跟蹤期望值，會有一定的損失。然而，預測控制區間的控制思想可以令被控變量跟蹤期望值在一定范圍內即可滿足控制。因此，控制人員在采用考慮裕量損失函數的預測控制進行控制時，需要合理選擇裕量損失函數的權重，在實現減少單次控制中操作變量消耗空間的同時，要確保被控變量在給定的區間范圍內。

5 仿真與示例

為驗證筆者所提方法的正確性，采用文獻[17]中的非等溫連續攪拌反應器系統(CSTR)進行仿真分析。其中y1、y2分別表示反應器的濃度與溫度，u1、u2分別表示進料濃度和冷卻液流量。

其線性離散狀態空間模型如下：

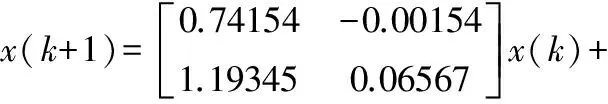
(17)

s.t. -1.5≤u1≤6,-1.5≤u2≤2

-1≤y1≤3,-1≤y2≤2

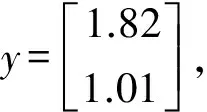
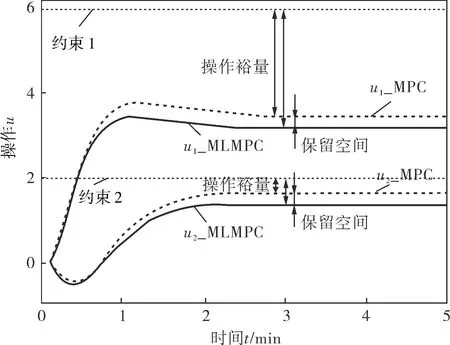
a. 操作變量的響應

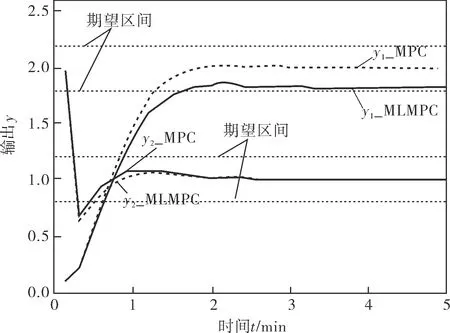
b. 輸出變量的響應

6 結束語

通過在常規預測控制的性能指標函數中加入一個能夠表示操作裕量變化情況的裕量損失函數，構建了考慮裕量損失函數的預測控制新架構，推導了考慮裕量損失函數的預測控制的優化求解過程，并通過穩態最優解分析了考慮裕量損失函數的預測控制保留操作變量空間的效果，同時分析了在預測控制中考慮裕量損失函數對控制效果的影響。考慮裕量損失函數的預測控制可以在控制的短周期動態控制過程中實時地實現保留操作變量的空間，不僅可以有效緩解邊界效應，保障裝置和生產的安全性，同時可以令控制的“好處”緩慢釋放，為后續的操作優化留出更多的空間和余地。

[1] 何偉,魯明,李國強,等.SNCR脫硝系統的廣義預測控制[J].石油化工自動化,2016,52(1):38～41.

[2] Xu F,Jiang H R,Wang R,et al.Influence of Design Margin on Operation Optimization and Control Performance of Chemical Processes[J].Chinese Journal of Chemical Engineering,2014,22(1):51～58.

[3] 羅雄麟,許鋒.過程控制與工藝設計一體化:催化裂化裝置動態機理建模與控制分析設計[M].北京:科學出版社,2008.

[4] 羅雄麟,周曉龍,王書斌.輸入變量關聯約束對約束優化控制的影響特性分析[J].自動化學報,2012,39(5):679～689.

[5] 左信,袁璞.區域預估控制初探·工業過程模型化及控制[M].廣州:華南理工大學出版社,1992.

[6] Kwon W H,Pearson A E.A Modified Quadratic Cost Problem and Feedback Stabilization of a Linear System[J].IEEE Trans Automat Control,1977,22(5):838～842.

[7] Kwon W H,Pearson A E.On Feedback Stabilization of Time-varying Discrete Linear Systems[J].IEEE Trans Automat Control,1993,38(10):1512～1516.

[8] Michalska H,Mayne D Q.Robust Receding Horizon Control of Constrained Nonlinear Systems[J].IEEE Transactions on Automatic Control,1993,38(11):1623～1633.

[9] 蕭明波,錢積新.預測控制中靜態目標的實現[J].控制理論與應用,1997,14(3):313～317.

[10] Sanchez-Sanchez K B,Ricardez-Sandoval L A.Simultaneous Design and Control under Uncertainty Using Model Predictive Control[J].Industrial & Engineering Chemistry Research,2013,52(13):4815～4833.

[11] 許鋒,羅雄麟.先進控制條件下化工過程操作裕量與控制性能分析[J].化工學報,2012,63(3):881～886.

[12] 羅雄麟,周衍彤.預測控制的哲學思想分析及其新架構的提出[J].化工進展,2017,36(3):783～790.

[13] Narraway L T,Perkins J D,Barton G W.Interaction between Ptocess Design and Process Control:Economic Analysis of Process Dynamics[J].Journal of Process Control,1991,1(5):243～250.

[14] 席裕庚.預測控制[M].北京:國防工業出版社,1993.

[15] 袁璞.生產過程動態數學模式及其在線應用[M].北京:中國石化出版社,1994.

[16] 袁璞.單值預估控制[J].中國石油大學學報(自然科學版),1992,16(5):100～109.

[17] Sanchez-Sanchez K B,Ricardez-Sandoval L A.Simultaneous Design and Control under Uncertainty Using Model Predictive Control[J].Industrial & Engineering Chemistry Research,2013,52(13):4815～4833.

NewFrameworkofModelPredictiveControlConsideringMarginLossFunction

ZHOU Yan-tong, LUO Xiong-lin, XU Feng
(CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum)

Basing on the performance index function of conventional predictive control, a margin loss function which representing the space variation of operating variables was added; and a new framework of model predictive control algorithm which considers margin loss function(MLMPC) was proposed and its optimization solution was derived. At the same time, having the steady optimal value used to analyze the effects of saving the space of operating variables and that of adding margin loss function to the predictive control. Finally, an example simulation is given to illustrate the effectiveness of this new algorithm.

continuously-stirred reactor, model predictive control, margin loss function

TQ021.8；TP273

A

1000-3932(2017)09-0823-07

2017-03-15，

2017-06-19)

周衍彤(1991-)，碩士研究生，從事過程控制的研究。

聯系人羅雄麟(1963-)，教授，從事控制理論與過程控制、化工系統工程及機器學習等的研究，luoxl@cup.edu.cn。