基于內模控制的Smith反向解耦控制器設計

王元飛 張曉靜 賈玉明

(海工英派爾工程有限公司自控室)

基于內模控制的Smith反向解耦控制器設計

王元飛 張曉靜 賈玉明

(海工英派爾工程有限公司自控室)

針對多變量時滯系統提出了一種基于內模控制(Internal Model Control，IMC)的Smith動態解耦控制器設計方法。其中，Smith補償器被應用在該控制結構中，包含帶有時滯項和不帶時滯項的補償結構，以解決不能完全補償的問題，通過反向解耦設計實現多變量時滯系統動態解耦。多變量系統被解耦成一系列互相獨立的單回路對象，通過內模控制原理對Smith控制器進行參數整定，并分析了系統的魯棒性。仿真實例表明了該方法的有效性，能夠較好地克服系統參數擾動導致的干擾，并具有較好的動態性能。

反向解耦 內模控制 Smith補償 多變量系統 時滯

現代工業過程大多以多變量系統形式存在，并有著大滯后特性[1,2]，例如化工蒸餾塔，而大滯后特性的存在增加了系統的不穩定性，使得控制設計變得更為困難。針對多變量特性，傳統的分布式控制采用一系列獨立的控制器，將多變量系統主回路對象考慮在內，往往不能在動態響應過程中消除控制回路之間的耦合，而無法獲得較好的控制特性[3,4]。基于此，集中式解耦控制器的研究變得更加迫切。

集中式解耦控制器按照過程解耦中是否考慮動態響應分為兩類：靜態解耦和動態解耦。靜態解耦在系統有著強耦合特性時，動態響應中耦合依然明顯存在[5～7]，而動態解耦方法可以很好地解決此問題。Gagnon E等討論了一系列的動態解耦控制方法[8]，其中包括理想解耦、反向解耦等，但對于大滯后系統的控制表現不佳；Wang Q等設計了一種基于內模控制的集中式控制器[9]，動態過程被充分考慮，然而大滯后影響仍未消除；Liu T等基于理想傳遞函數提出了一種反向解耦結構的控制方法[10]，詳細分析了該方法的系統魯棒性，該方法設計較為簡單，且能夠獲得較好的解耦效果；Kumar V V等提出了一種直接設計方法[7]，其中過程的逆函數可以近似得到，但由于高階的存在，工程中較難實現；王富強等針對時滯多變量系統高階設計的復雜性[11]，提出了一種基于模型降解的解耦控制方法，降低了設計難度，但同時降解所帶來的誤差也影響了系統解耦效果；Raviteja K等為解決不穩定系統TITO提出了一種基于改進ETF(Equivalent Transfer Function)的解耦控制方法[12]，而此方法并非直接設計方法，依然會帶來控制誤差。

在消除多變量系統耦合的同時，為了解決多變量系統時滯帶來的控制不穩和滯后問題，時滯多變量系統Smith靜態解耦控制取得了不少成果[13～15]，但無法有效地補償時滯項帶來的影響。Smith動態解耦控制并沒有取得多少研究進展，其原因在于不能很好地對系統時滯項進行完全補償。筆者提出了一種新的補償方法，在Smith控制結構的基礎上，采用反向解耦對大時滯特性進行了完全的補償控制，并能夠獲得較好的解耦效果，通過內模控制方法整定系統PID參數。

1 Smith完全補償設計

Smith完全補償結構如圖1所示，C(s)為Smith控制器，Gp(s)和Gm(s)分別為m階(m×m)系統過程函數和系統模型函數。

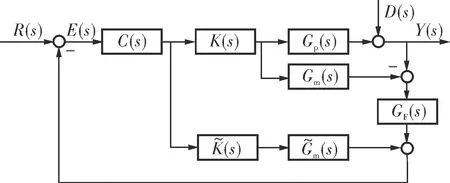
圖1 Smith完全補償控制結構

假設解耦器K(s)能夠將過程解耦為下式：

Gp(s)K(s)=Qi(s)=diag{q1(s)e-τ1s,q2(s)e-τ2s,…,qm(s)e-τms}

(1)

其中，qi為不含有滯后項的正定傳遞函數。要能夠對時滯項進行完全補償則必須達到以下條件：

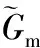
(2)

則當系統模型匹配時，即Gp(s)=Gm(s)，系統最終傳遞函數為：

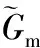
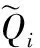
(3)

選定反向解耦器K(s)結構如圖2所示。

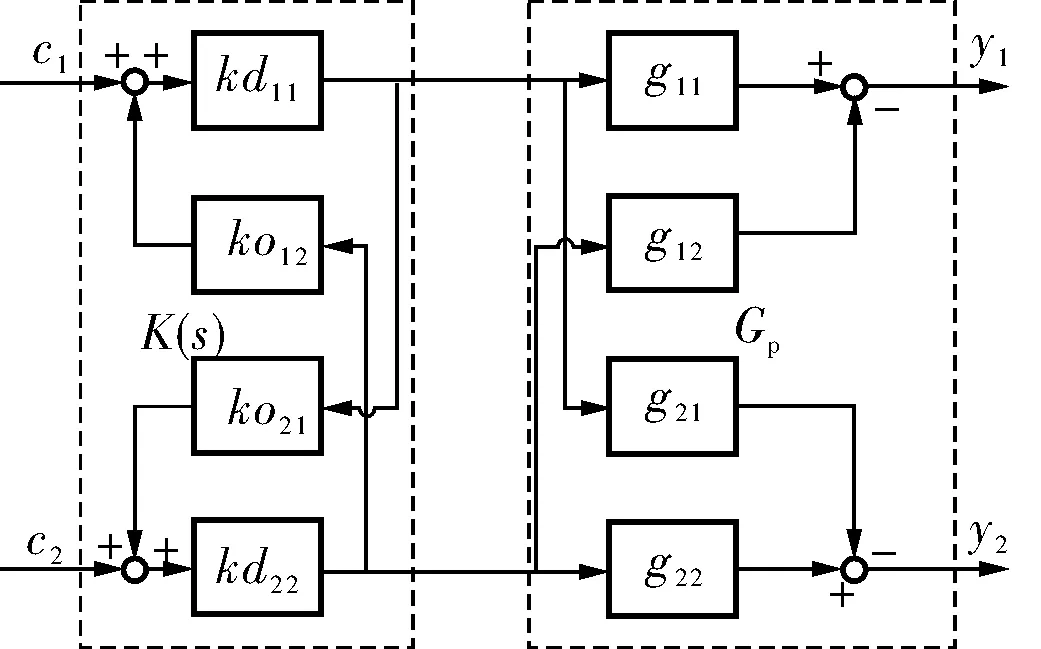
圖2 反向解耦器結構

計算解耦器K(s)：

K(s)=Kd(s)[I(s)-Ko(s)Kd(s)]-1

(4)

最終控制器輸出C(s)與系統輸出Y(s)的關系為：

Y(s)=G(s)K(s)C(s)

(5)

式(5)中,令Q(s)=G(s)K(s)，Q(s)被定義為系統的廣義傳遞函數，因此，容易通過其逆形式得到K(s)為：

K(s)=G-1(s)Q(s)

(6)

為方便計算，由式(4)取其逆并將它代入式(6)中得到：

Kd-1(s)-Ko(s)=Q-1(s)G(s)

(7)

通過確定理想傳遞函數Q(s)，由式(7)可方便得到反向解耦器形式。由于反向解耦器的特殊形式，解耦器可使得理想傳遞函數正定部分和純滯后部分分開處理，這是實現Smtih完全補償的重要條件。

2 控制器設計與性能分析

考慮到IMC控制器設計的簡易性，可得出Smith控制器與IMC控制器之間的轉換關系，從而得出Smith控制器的形式。針對控制器參數整定，考慮不確定性下系統的魯棒性能，并對它進行計算分析。

2.1 控制器設計

Smith控制器是在系統被解耦為理想傳遞函數的情況下設計，系統各回路之間不存在耦合關系，因此Smith控制器與IMC控制器的等效關系為：

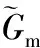
(8)

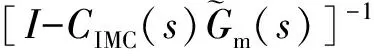
依據內模設計原理，IMC控制器為：

(9)

其中，Qii-(s)不含有右半平面極點和時滯部分，即正定部分；階次n最小值為IMC控制器實現有理的取值；濾波器參數λi影響系統一般性能和魯棒性能，其值的選取應平衡上述性能指標。

當系統模型匹配時，第i回路Smith控制器為：

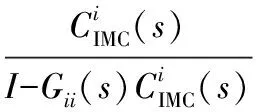
(10)

在現實工況中，為了保證系統魯棒穩定性和系統性能的平衡，參數λ一般以逐漸增大的方式來選取，故將系統加性不確定性考慮在內，如圖3所示。

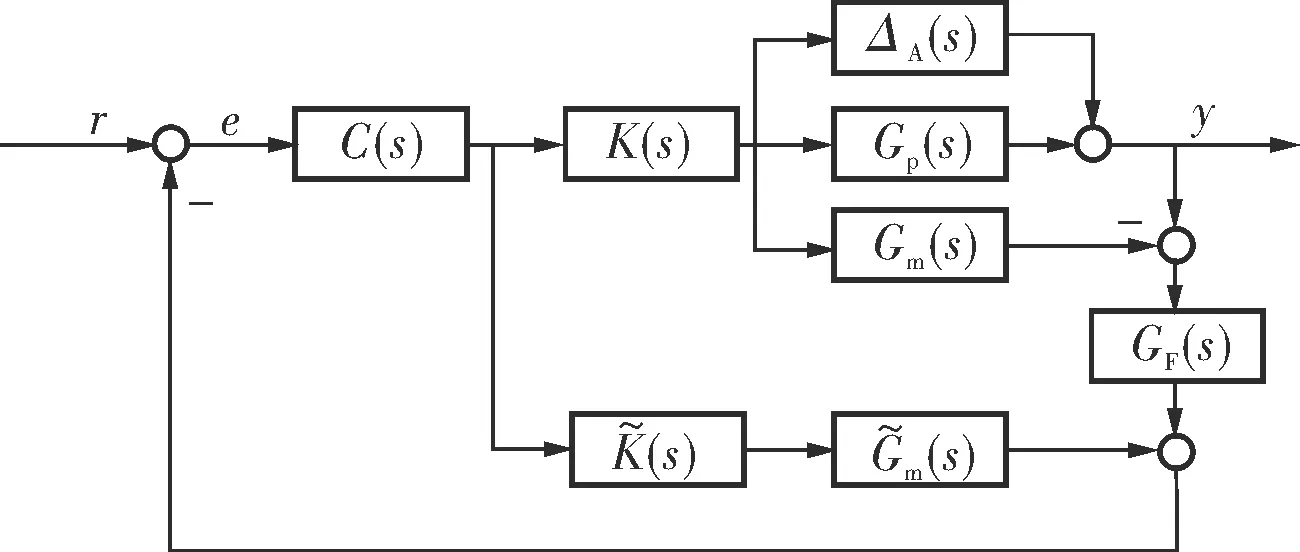
圖3 系統加性不確定性結構

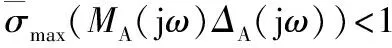
(11)

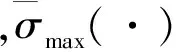
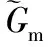
(12)

2.2 性能分析

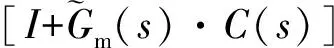
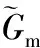
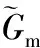
(13)

依據小增益定理，在無法具體表述不確定形式時，采取最大奇異值倒數指標：

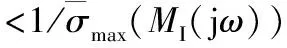
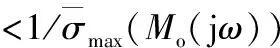
(14)

式即系統魯棒穩定性能指標RS，而系統魯棒性能指標RP表述如下：

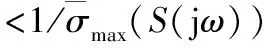
(15)

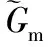
(16)

其中S(s)表示系統靈敏度函數，式(16)的成立保證了系統的內部穩定性，且可求出最大可承受干擾。

3 實例仿真

對于經典TITO的Wood-Berry模型：

選定廣義對象傳遞函數如下：

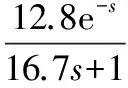
針對廣義對象，設計的簡化Smith控制器如下：

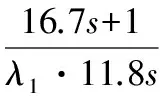
其中純滯后項用一階泰勒近似。為整定濾波器參數λ，計算不同參數下式(11)在各頻率下的最大奇異值，計算結果如圖4所示。考慮系統跟蹤性能、超調量等一般性能和系統魯棒性能的平衡，選取濾波器參數λ1=λ2=5。

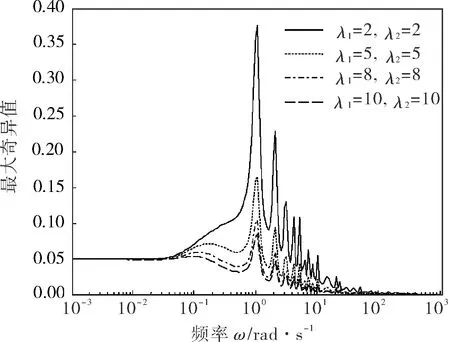
圖4 加性不確定性下最大奇異值

圖5為系統模型匹配時輸入為單位階躍信號系統輸出和控制器輸出仿真圖像，單位階躍時間分別在t=10s和t=100s，為比較設計方法的優越性，將另外兩種方法[5, 17]與筆者所提方法進行比較。從圖5中可以看出，筆者所提方法能夠獲得更好的動態跟蹤響應，在克服大滯后存在的同時，動態解耦效果顯著。

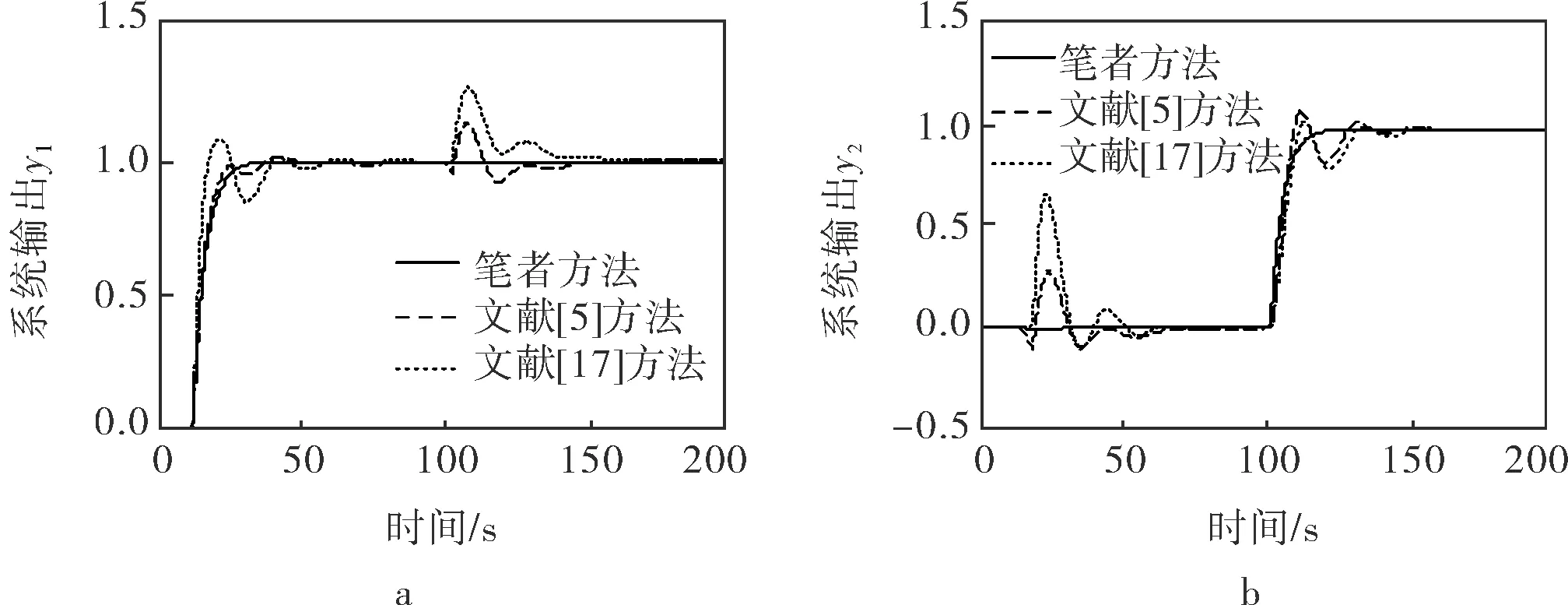
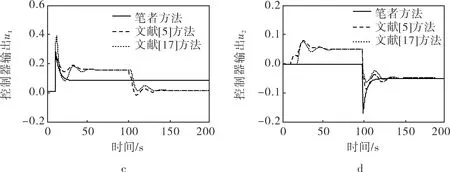
圖5 模型匹配時系統和控制器輸出

為評價系統魯棒穩定性和魯棒性能，分別就輸入不確定性、輸出不確定性和靈敏度函數通過式(14)、(15)仿真各頻率下最大奇異值倒數(圖6)。從圖6中可以看出，在兩種不確定情況下，系統均能夠保證很好的魯棒穩定性，求得其穩定裕度分別為70.3%和100%，針對靈敏度函數其裕度為72.0%。

為更加清楚地展示系統的魯棒性能，系統增益和純滯后時間均有+30%的攝動，而-30%系統參數攝動加于時間常數。由圖7可以看出，筆者設計的方法在系統失配時更能夠保證系統的動態性能，這足夠證明了該設計方法擁有較好的魯棒性能。

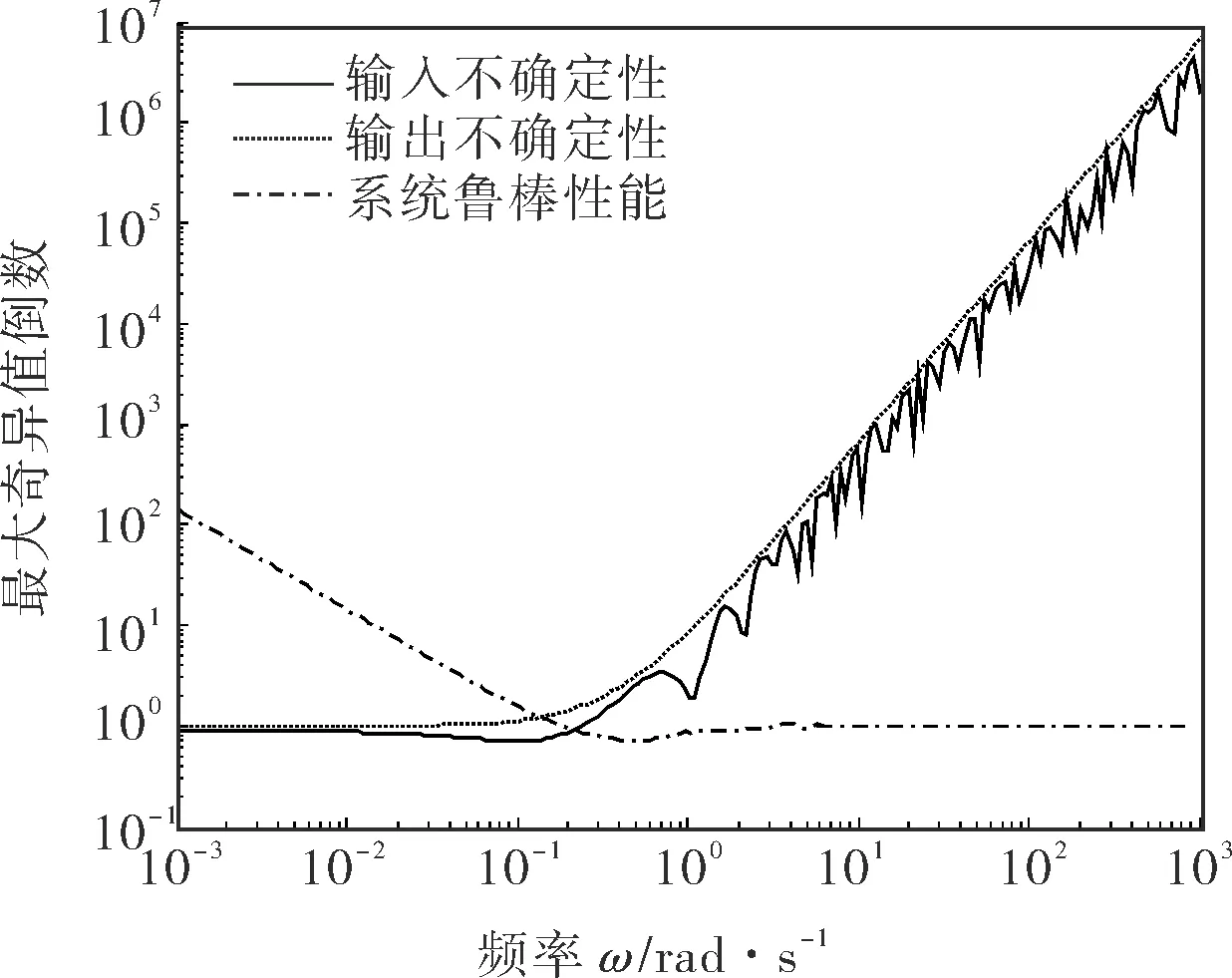
圖6 各不確定性下最大奇異值倒數

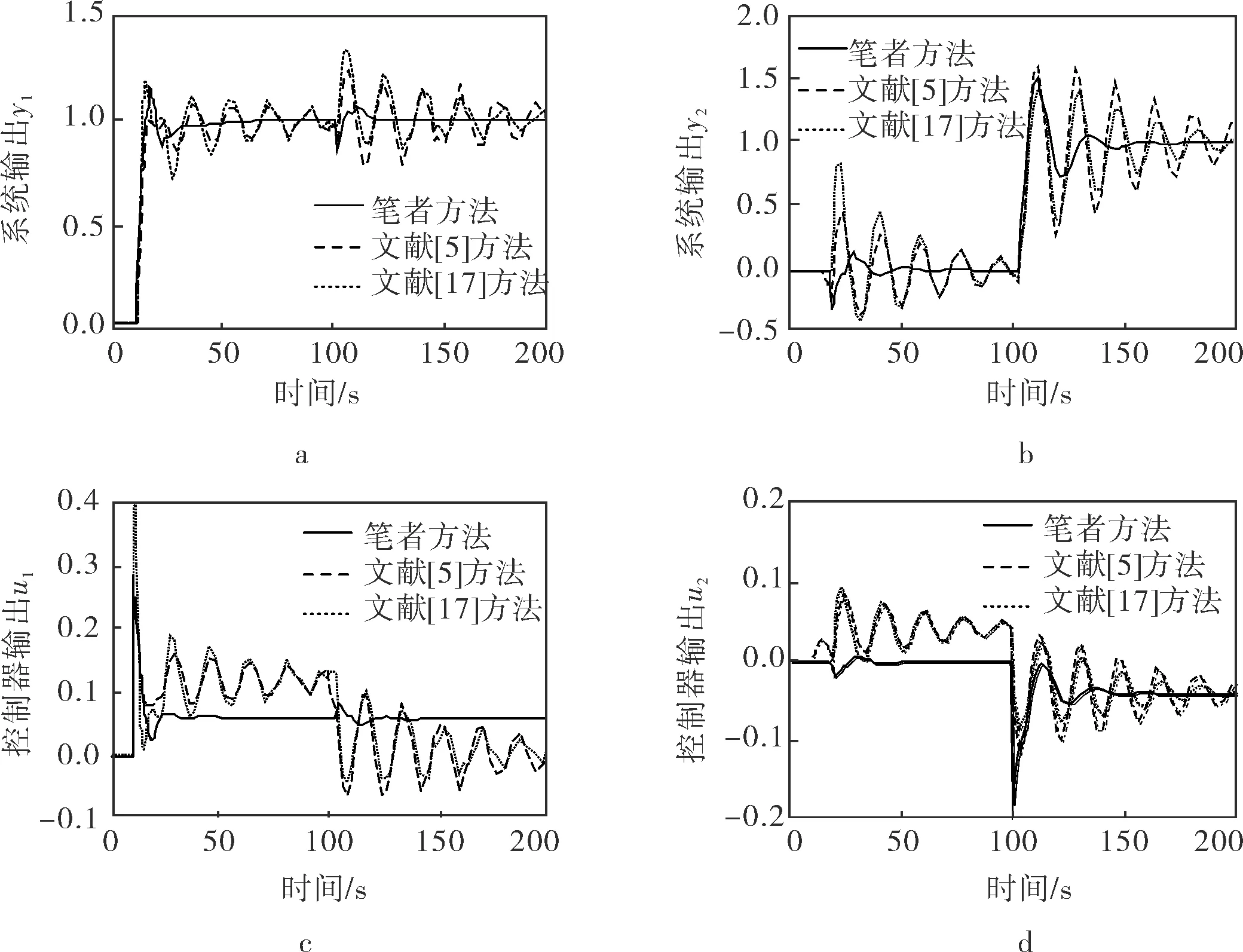
圖7 模型失配時系統和控制器輸出

為綜合比較3種方法的性能指標，系統超調量、上升時間、ISE和IAE計算結果見表1。

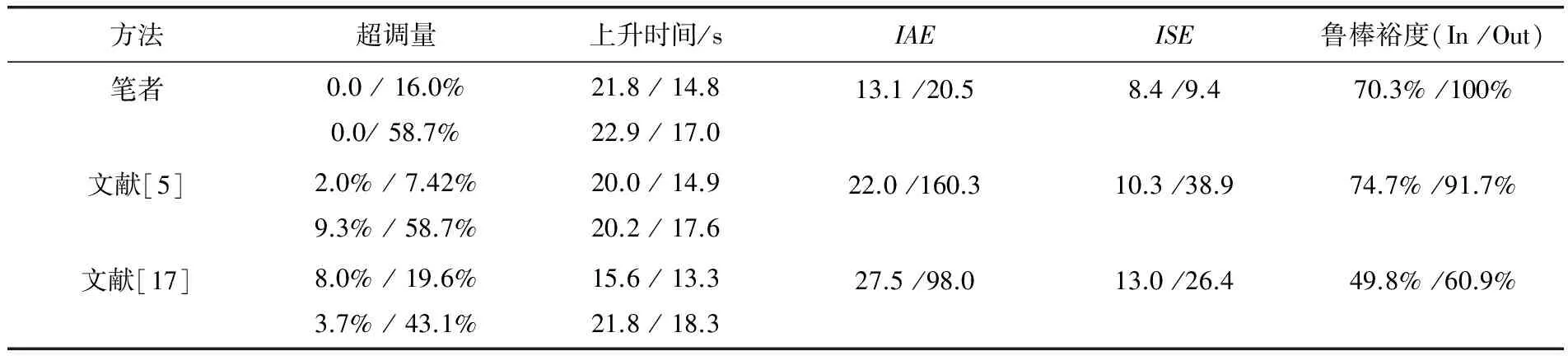
表1 各指標數值 (標配/失配)

4 結束語

設計了一種基于反向解耦的Smith完全補償控制結構，通過將系統不帶時滯項和時滯項分離，能夠消除Smith控制時動態解耦不完全產生的誤差。控制器參數通過內模原理進行整定，易于計算，并就動態性能和魯棒性能進行了系統性分析，給出了實例仿真。筆者所提方法在消除多變量系統耦合的同時，保證了系統的動態性能和魯棒性能的平衡，仿真證明了方法的有效性。

[1] Alatiql I M, Luyben W L.Control of a Complex Sidestream Columnstripper Distillation Configuration[J]. Ind Eng Chem Process Des Dev, 1986, 25(3): 762～767.

[2] Ogunnaike B A, Lemaire J P, Morari M, et al. Advanced Multivariable Control of a Pilot-Plant Distillation Column[J]. AICHE Journal, 1983, 29(4): 632～640.

[3] Nordfeldt P, Hagglund T. Decoupler and PID Controller Design of TITO Systems[J]. Journal of Process Control, 2006, 16(9): 923～936.

[4] Maghade D K, Patre B M.Decentralized PI/PID Controllers Based on Gain and Phase Margin Specifications for TITO Processes[J]. ISA Transactions, 2012, 51(4): 550～558.

[5] Lee J, Dong H K, Edgar T F. Static Decouplers for Control of Multivariable Processes[J]. AICHE J, 2005, 51(10): 2712～2720.

[6] Qiang X, Wen J C, Mao J H. Equivalent Transfer Function Method for PI/PID Controller Design of MIMO Processes[J]. Journal of Process Control, 2007, 17(8): 665～673.

[7] Kumar V V, Rao V S R, Chidambaram M.Centralized PI Controllers for Interacting Multivariable Processes by Synthesis Method [J]. ISA Transactions, 2012, 51(3): 400～409.

[8] Gagnon E, Pomerleau A, Desbiens A. Simplified, Ideal or Inverted Decoupling[J]. ISA Transactions, 1998, 37(4): 265～276.

[9] Wang Q,Zhang Y,Chiu M. Decoupling Internal Model Control for Multivariable Systems with Multiple Time Delays[J]. Chemical Engineering Science, 2002, 57(1): 115～124.

[10] Liu T, Zhang W, Gao F.Analytical Decoupling Control Strategy Using a Unity Feedback Control Structure for MIMO Processes with Time Delays[J]. Journal of Process Control, 2007, 17(2): 173～186.

[11] 王富強, 李曉理, 張秋生,等. 基于模型降階的時滯多變量系統動態解耦[J]. 控制工程, 2015, 22(4): 639～644.

[12] Raviteja K, Purushottama R D,Rao A S. Improved Controller Design for Two-Input-Two-Output(TITO) Unstable Processed[J]. Resource-Efficient Technologies, 2016, 2(3): 76～86.

[13] Chen J, He Z F,Qi X. A New Control Method for MIMO First Order Time Delay Non-Square Systems[J]. Journal of Process Control, 2011, 21(4): 538～546.

[14] Santos T L M, Bismark C T, Julio E N. Simplified Filtered Smith Predictor for MIMO Processes with Multiple Time Delays[J]. ISA Transactions, 2016, 65:339～349.

[15] Raja G L, Ahmad A. Smith Predictor Based Parallel Cascade Control Strategy for Unstable and Integrating Processes with Large Time Delay[J]. Journal of Process Control, 2017, 52: 57～65.

[16] Skogestad S, Postlethwaite I. Multivariable Feedback Control:Analysis and Design[M]. New York:Wiley, 2007.

[17] 陳強, 欒小麗, 劉飛.高維多變量時滯系統多環PI控制的解析設計[J].信息與控制, 2014, 43(2):205～210.

[18] Lee J, Kim D H, Edgar T F. Static Decouplers for Control of Multivariable Processes[J].AICHE Journal, 2005, 51(10):2712～ 2720.

SmithInvertedDecouplingControllerDesignBasedonInternalModelControl

WANG Yuan-fei, ZHANG Xiao-jing, JIA Yu-ming
(ControlDept.,COUEC-EnpalEngineeringCo.,Ltd.)

The design of dynamic Smith decoupling controller based on internal model control (IMC) was proposed for the multivariable system with time-delays, in which, Smith compensator with and without the delay terms was employed for the control scheme and to solve incomplete compensation; and through the reverse decoupling design, the dynamic decoupling of the multivariable system with time-delays can be realized. Having the multivariable system decomposed into a set of mutually independent single loops and having IMC theory based to set parameters of Smith controller were implemented, including analysis of system robustness. Simulation examples demonstrate the effectiveness of the proposed approach, and it can eliminate the disturbance incurred by the system parameter perturbation together with good dynamic property.

inverted decoupling, IMC, Smith compensation, multivariable system, time delay

TP273

A

1000-3932(2017)09-0830-06

2017-03-21，

2017-04-18)

王元飛(1989-)，助理工程師，從事復雜系統控制與設計、化工自控系統設計以及系統安全評估工作，youyou7003@126.com。