非線性光纖方向耦合器中的行波解及動力學行為
吳曉飛,華國盛
(1.麗水學院工學院,浙江麗水323000;2.麗水學院信息技術中心,浙江麗水323000)
非線性光纖方向耦合器中的行波解及動力學行為
吳曉飛1,華國盛2
(1.麗水學院工學院,浙江麗水323000;2.麗水學院信息技術中心,浙江麗水323000)
借助于著名的齊次平衡原理和F-展開法的基本思想,研究非線性光纖方向耦合器系統中的非線性薛定諤方程組,得到滿足傳輸方程的多種Jacobi橢圓函數周期波解和亮孤子解,并通過圖形分析法,討論其中一些解的動力學行為。
非線性薛定諤方程組;F-展開法;亮孤子解
0 引言
自從1980年Mollenauer、Stolen和Gordon[1]在實驗室首次驗證了光纖中可傳輸孤立子以來,光孤子在光纖中的傳輸理論與實驗一直是人們的研究熱點之一。由于光孤子在單模光纖中傳輸時可以保持形狀不變,這為超高碼速光纖通信提供了可能性。近年來,美、日、英等許多國家都致力于進行光孤子通信傳輸的實驗,大力研發這一技術。例如,美國AT&T公司與日本KDD公司合作建設的越洋海底光纜,即TPC-6工程,就采用了光孤子傳輸技術,其傳輸能力達到了100 Gbit/s,距離在10 000 km以上。目前,光孤子傳輸實驗的研究已獲得了突破性的進展,其傳輸的碼率和傳輸的距離分別可達到160 Gbit/s和106km以上,這為其實用化又更進了一步。然而,一個實用的全光孤子通信系統除了作為傳輸線的單模光纖以外,還包括脈沖變換器件,如光開關、光方向耦合器等。因此,研究光孤子在這些器件中的演化過程及其動力學行力,具有重要的理論意義和實際的應用價值。
非線性雙芯光纖方向耦合器中的脈沖傳輸,在忽略交錯相位調制的情況下,通常滿足如下非線性薛定諤方程組
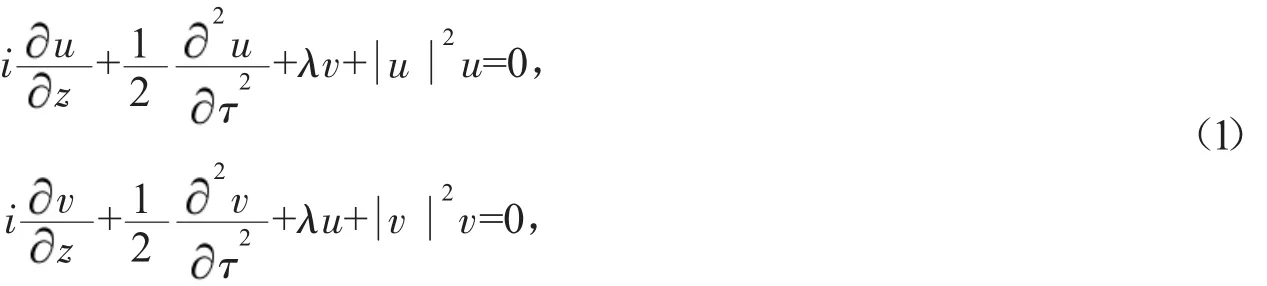
式中u,v分別為歸一化后的1芯層和2芯層孤子振幅,z,τ,λ分別為歸一化的距離、時間和耦合系數。若λ=0,則方程組(1)就變為兩個獨立的非線性薛定諤方程,可以用反散射法精確地求出其N-孤子解。但由于交叉耦合的存在,方程組(1)是不可積的。本文擬利用著名的齊次平衡原理[2]和F-展開法[3]的基本思想來研究非線性光纖方向耦合器系統中的非線性薛定諤方程組,得到了滿足傳輸方程的多種Jacobi橢圓函數周期波解和亮孤子解。
1 非線性薛定諤方程組的求解
首先對方程組(1)作行波約化,設

式中 ξ=z+cgτ,η=kz+ωτ,cg為群速,k 為波數,ω 為角頻率。
將式(2)代入方程組(1)得φ,ψ滿足的非線性常微分方程組
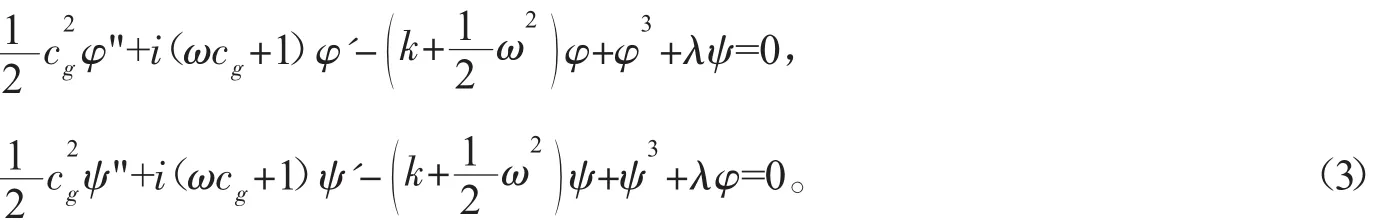
通常我們要求φ,ψ是實函數形式,故要求φ',ψ'前的復系數為零,取ωcg+1=0,則方程組(3)簡化為

依據F-展開法的基本思想,設方程組(4)的解的形式為
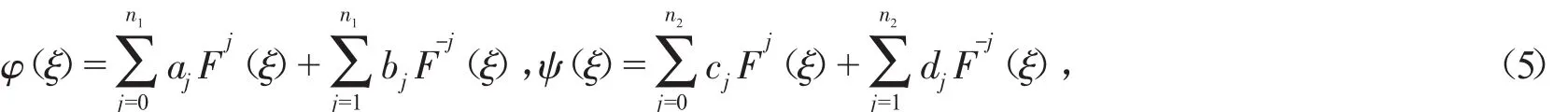
式中 n1,n2為正整數,a0,a1,…,an1,b1,…,bn1,c0,c1,…,cn2,d1,…,dn2為待定常數。F(ξ)滿足常微分方程

式中P,Q,R為待定常數。
通過平衡方程組(4)中的最高階導數項與非線性項,可確定n1=n2=1,于是由式(5)得到

式中,a0,a1,b1,c0,c1,d1為待定常數。
將式(7)代入方程組(4),并利用式(6),合并F的同次冪項的系數,令F的各次冪項的系數為零,得到關于 a0,a1,b1,c0,c1,d1,cg,k,ω,P,Q,R 的代數方程組。然后,利用 maple軟件解此代數方程組,可得滿足方程組的解為:
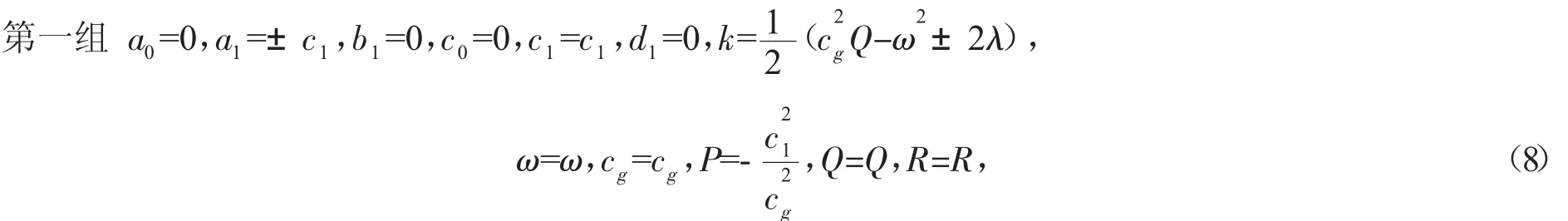
其中 c1,ω,cg,Q,R 為任意實數,且 ωcg+1=0;
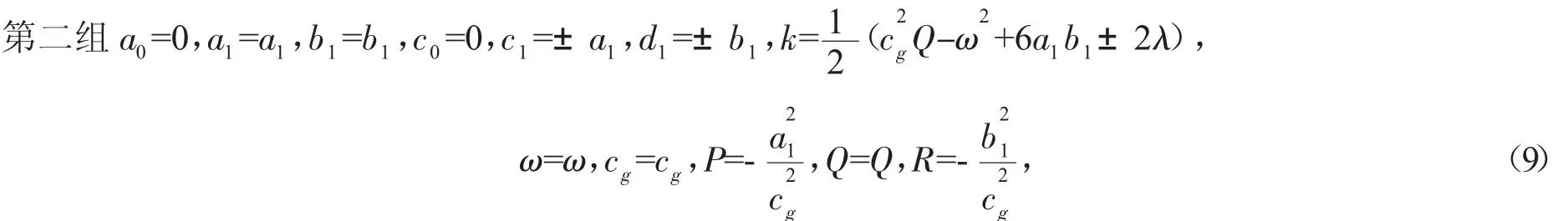
其中 a1,b1,ω,cg,Q 為任意實數,且 ωcg+1=0。
2 非線性薛定諤方程組的解的討論
根據方程(6)、式(7)~ 式(9)和式(2),選取不同的 P、Q、R 值,可分別確定方程組(1)的不同的 Jacobi橢圓函數周期波解及孤子解。
2.1 Jacobi橢圓函數周期波解
(1)取P=-m2,Q=2m2-1,R=1-m2(m為Jacobi橢圓函數的模)時,F=cn(ξ),則方程組(1)的解為
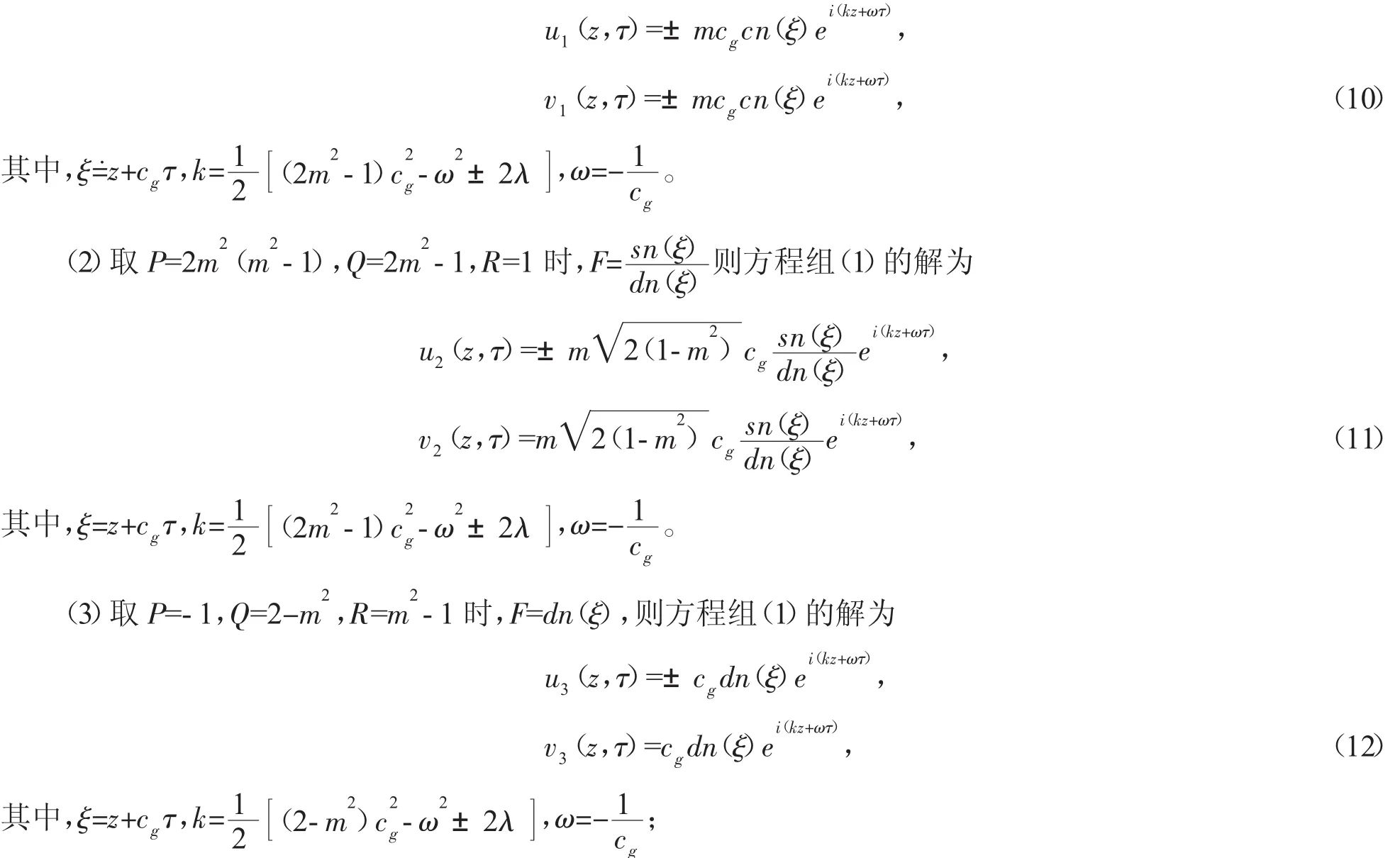

2.2 孤子解
當m→1時,由式(10)表示的Jacobi橢圓函數周期波解就退化為如下亮孤子解

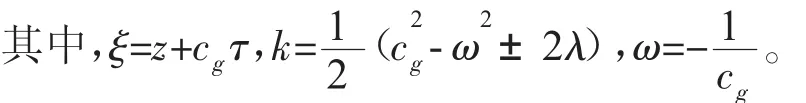
2.3 圖形分析
為了更直觀地了解Jacobi橢圓函數周期波以及孤波的特性,利用計算機Maple軟件對典型解進行模擬作圖分析。
與解 u1的模所對應的周期波結構如圖(1)所示,(a)取 cg=1,m=0.8時隨 t變化的波形圖,(b)取 cg=1,m=0.8,t=0時的波形截面圖。與解u5的模所對應的m型周期波結構如圖(2)所示,(a)取cg=1,m=0.1時隨t變化的波形圖,(b)取cg=1,m=0.1,t=0時的波形截面圖。與解u6的模對應的類w型周期波結構如圖(3)所示,(a)取cg=1,m=0.2時隨t變化的波形圖,(b)取cg=1,m=0.2,t=0時的波形截面圖。與解 u7的模所對應的w 型周期波結構如圖(4)所示,(a)取 cg=1,m=0.1 時隨 t變化的波形圖,(b)取 cg=1,m=0.1,t=0 時的波形截面圖。與解u8的模對應的w-m組合型周期波結構如圖(5)所示,(a)取cg=1,m=0.75時隨t變化的波形圖,(b)取cg=1,m=0.75,t=0時的波形截面圖。與解u9的模所對應的孤波結構及孤波隨時間的演化圖如圖(6)所示,(a)取 cg=1 時隨 t的變化波形圖,(b)取 cg=1,t=-5(實線),t=5(虛線)時的波形截面圖,它是左行波,由實線曲線移動到虛線曲線。
因為u=±v,所以u的模的圖形與v的模的圖形是一致的。
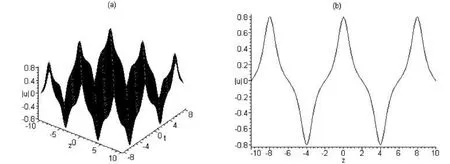
圖1 與解u1的模對應的周期波結構圖((a)取cg=1,m=0.8時隨t變化的波形圖;(b)取cg=1,m=0.8,t=0時的波形截面圖)
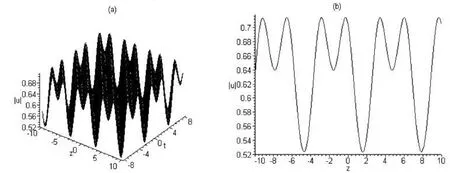
圖2 與解u5的模對應的m型周期波結構圖((a)取cg=1,m=0.1時隨t變化的波形圖;(b)取cg=1,m=0.1,t=0時的波形截面圖)
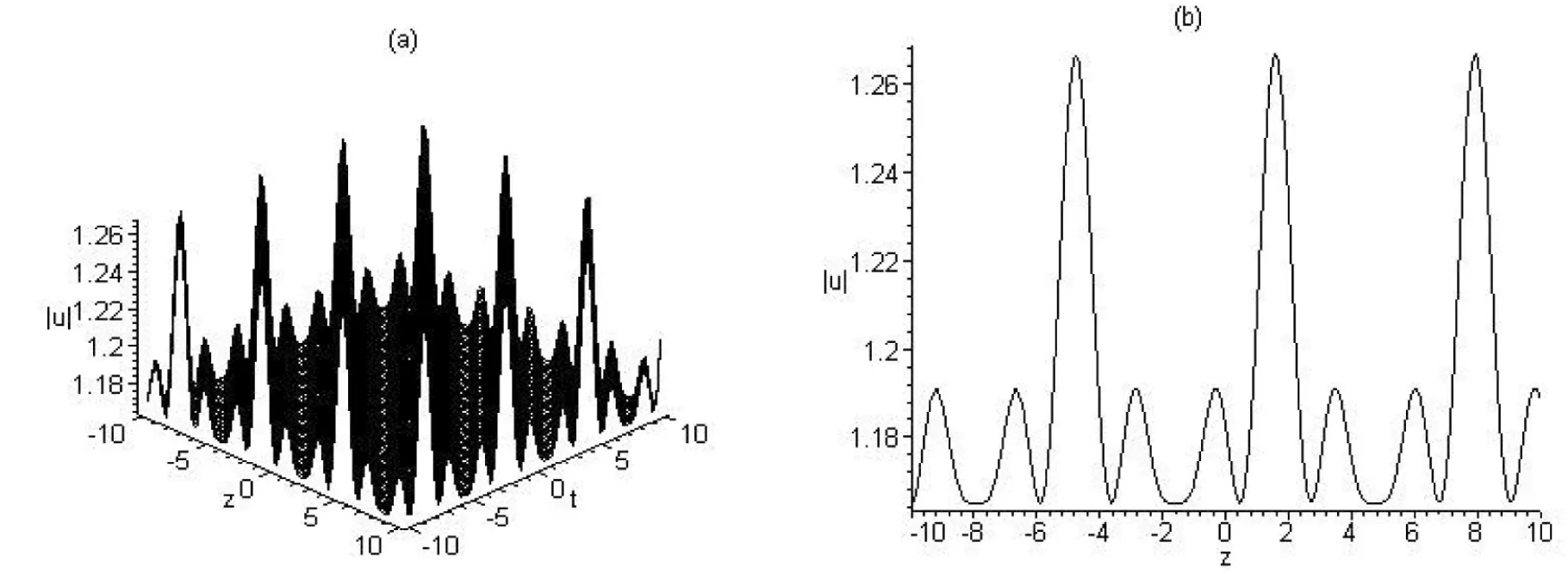
圖3 與解u6的模對應的類w型周期波結構圖((a)取cg=1,m=0.2時隨t變化的波形圖;(b)取cg=1,m=0.2,t=0時的波形截面圖)
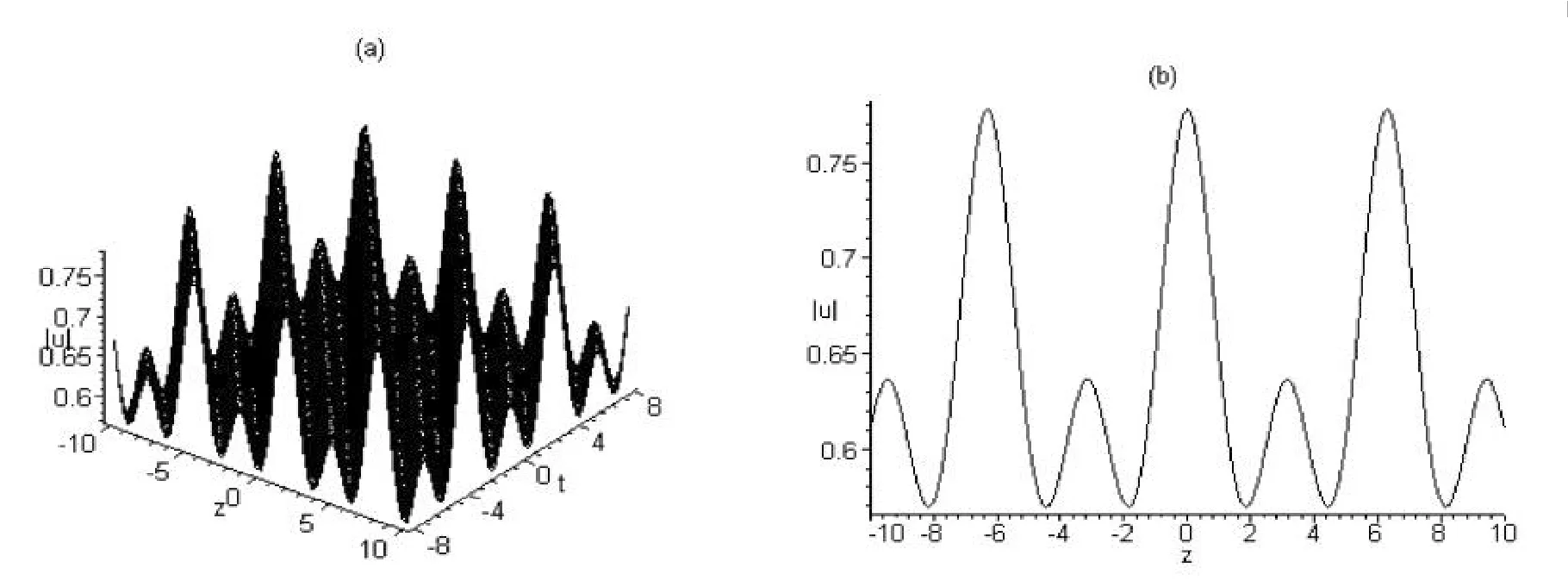
圖4 與解u7的模對應的w型周期波結構圖((a)取cg=1,m=0.1時隨t變化的波形圖;(b)取cg=1,m=0.1,t=0時的波形截面圖)
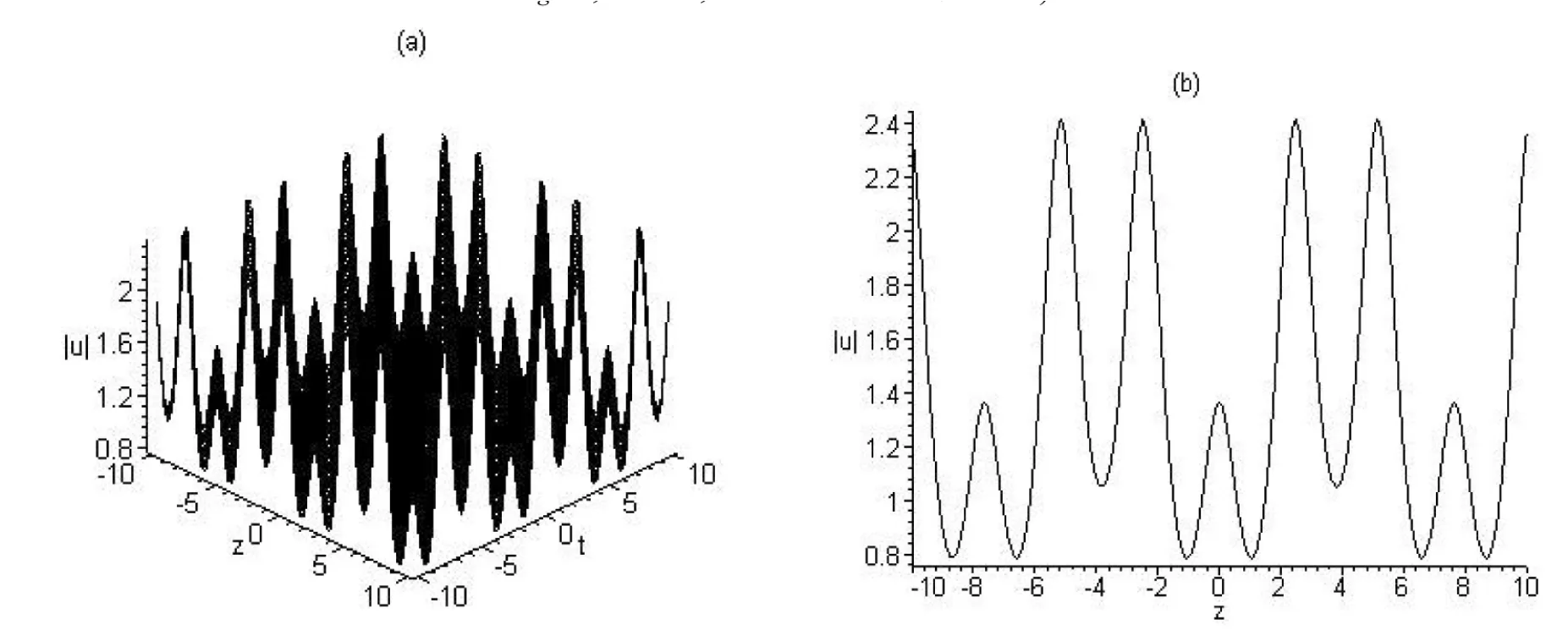
圖5 與解u8的模對應的w-m組合型周期波結構圖((a)取cg=1,m=0.75時隨t變化的波形圖;(b)取cg=1,m=0.75,t=0時的波形截面圖)
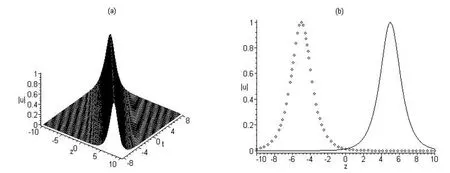
圖6 與解u9的模對應的孤波結構及孤波隨時間演化圖((a)取cg=1時隨t變化的波形圖;(b)取cg=1,t=-5(實線),t=5(虛線)時的波形截面圖)
3 結論
借助于著名的齊次平衡原理和F-展開法的基本思想,研究了非線性雙芯光纖方向耦合器中的脈沖傳輸所滿足的非線性薛定諤方程組,得到了滿足傳輸方程的多種顯式精確行波解,其解包括了Jacobi第二類、第三類函數以及由它們組成的其它形式的周期波解和亮孤子解,并通過圖形分析法,討論了幾種典型的特殊的周期波結構、孤波結構以及孤波隨時間的演化。與以往的研究成果[4-7]相比,圖3、圖5所示的周期波結構隨時間的演化是新的。在今后還將作進一步研究。
[1]MOLLENAUER LF,STOLEN R H,GORDON J P.Experimental observation ofpicosecond pulse narrowing and solitons in optical fibers[J].Phys RevLett,1980,45(9):1095.
[2]WANG M L,ZHOU Y B,LI Z B.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Physics Letters A,1996,216(1):67.
[3]LI BA,WANGML.Applications ofF-expansion method tothe coupled KdVsystem[J].Chin PhysB,2005,14(9):1698.
[4]MA Z Y,MA S H.Analytical solutions and rogue waves in(3+1)-dimensional nonlinear Schrdinger equation[J].Chin Phys B,2012,21(3):030507
[5]ZHU H P.Nonlinear tunneling for controllable rogue waves in two dimensional graded-index waveguides[J].Nonlinear Dyn,2013,72(4):873.
[6]DAI C Q,WANG Y Y,CHEN J L.Analytic investigation on the similariton transmission control in the dispersion decreasing fiber[J].Opt Commun,2011,284:3440.
[7]WU X F,HUA G S,MA Z Y.Novel rogue waves in an inhomogenous nonlinear medium with external potentials[J].Commun Nonlinear Sci Numer Simulat,2013,18(12):3325.
Dynamic Behaviors of the Solutions in Nonlinear Optical Fiber Coupler Schrodinger Equations
WUXiaofei1,HUAGuosheng2
(1.FacultyofEngineering,Lishui University,Lishui 323000,Zhejiang;2.Center ofInformation Technology,Lishui University,Lishui 323000,Zhejiang)
In this paper,the F-expansion and homogeneous balance method are used to solve the nonlinear optical fiber coupler Schrdinger equations.With this method,many kinds of explicit and exact traveling wave solutions are acquired,including Jacobi doubly periodic solutions and bright soliton.Besides,the dynamic behaviors of some solutions are discussed by direct computer simulations
coupler Schrdinger Equations;F-expansion;bright soliton
10.3969/j.issn.2095-3801.2017.05.001
O411.1
A
2095-3801(2017)05-0001-07
2017-02-15;
2017-03-20
浙江省自然科學基金資助項目“非線性動力系統的狄拉克結構約化”(LY14A010005)
吳曉飛,女,浙江縉云人,教授,碩士。

