基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的合金裂紋診斷技術(shù)
杜 鴻,楊 毅
(麗水學(xué)院工學(xué)院,浙江麗水323000)
基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的合金裂紋診斷技術(shù)
杜 鴻,楊 毅
(麗水學(xué)院工學(xué)院,浙江麗水323000)
給出一種基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的合金裂紋診斷技術(shù)。首先,建立一個(gè)具有單隱層結(jié)構(gòu)的輸入輸出模型來(lái)表示合金裂紋增長(zhǎng)過(guò)程。然后,利用超限學(xué)習(xí)機(jī)對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練,即在合適的范圍內(nèi)隨機(jī)給定網(wǎng)絡(luò)的內(nèi)權(quán),對(duì)外權(quán)則通過(guò)最小二乘法來(lái)進(jìn)行全局優(yōu)化,從而實(shí)現(xiàn)對(duì)合金裂紋增長(zhǎng)的診斷和預(yù)測(cè)。
單隱層前饋神經(jīng)網(wǎng)絡(luò);超限學(xué)習(xí)機(jī);合金裂紋
0 引言
合金裂紋增長(zhǎng)趨勢(shì)的診斷,對(duì)于預(yù)測(cè)機(jī)械設(shè)備的安全使用壽命以及故障診斷來(lái)說(shuō)是至關(guān)重要的。這方面的研究主要基于以裂紋長(zhǎng)度和開(kāi)裂壓力為狀態(tài)變量的疲勞裂紋變化的狀態(tài)方程[1-5]。此狀態(tài)方程是包含了高非線性項(xiàng)的一階差分方程,具有一步預(yù)測(cè)的能力。然而,由于此模型參數(shù)需要實(shí)驗(yàn)數(shù)據(jù)迭代計(jì)算獲得,模型的準(zhǔn)確性在很大程度上依賴于對(duì)裂紋長(zhǎng)度、開(kāi)裂壓力等因素的準(zhǔn)確測(cè)量上。而且,由于非線性項(xiàng)的存在以及裂紋增長(zhǎng)過(guò)程的復(fù)雜性,研究人員通常利用大量的實(shí)驗(yàn)數(shù)據(jù)來(lái)建立表格,并以查表的方式獲得與裂紋增長(zhǎng)相關(guān)的參數(shù)。這種方法的缺點(diǎn)是費(fèi)時(shí)且不能適應(yīng)環(huán)境條件的變化。另外,基于一階差分方程的裂紋長(zhǎng)度計(jì)算依賴于精準(zhǔn)的開(kāi)裂壓力數(shù)據(jù)。當(dāng)開(kāi)裂壓力數(shù)據(jù)不是相當(dāng)精準(zhǔn)時(shí),此模型不能準(zhǔn)確預(yù)測(cè)裂紋的增長(zhǎng)。為克服上述問(wèn)題,在這篇文章中,我們考慮用一個(gè)具有單隱層前饋神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的輸入輸出模型來(lái)描述裂紋增長(zhǎng)過(guò)程。選取開(kāi)裂壓力作為輸入數(shù)據(jù),裂紋長(zhǎng)度作為輸出數(shù)據(jù)來(lái)建立一個(gè)簡(jiǎn)化的裂紋增長(zhǎng)模型。運(yùn)用極限學(xué)習(xí)機(jī)算法,在合適的范圍內(nèi)隨機(jī)給定內(nèi)權(quán),并運(yùn)用最小二乘法來(lái)優(yōu)化確定外權(quán)。仿真結(jié)果將表明,基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的裂紋增長(zhǎng)模型能對(duì)裂紋的增長(zhǎng)過(guò)程起到很好的預(yù)測(cè)和診斷效果。
1 問(wèn)題描述
在工程領(lǐng)域,疲勞裂紋的增長(zhǎng)經(jīng)常用以下具有高非線性項(xiàng)的一階差分方程來(lái)描述[1-5]:

其中
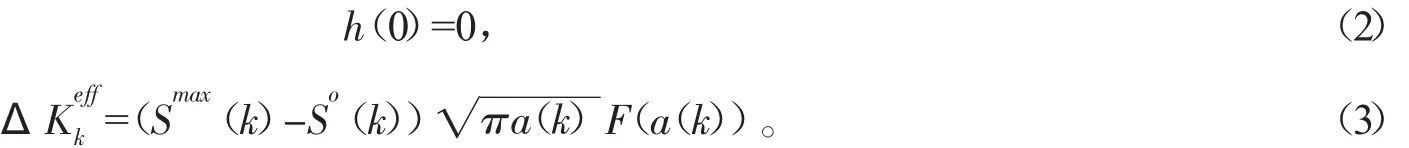
這里a(k)表示k次迭代后的裂紋長(zhǎng)度,h(ΔKekff)是非負(fù)單調(diào)遞增函數(shù),ΔKekff是有效壓力強(qiáng)度因素范圍,Smax(k)和 So(k)分別表示最大遠(yuǎn)程壓力和開(kāi)裂壓力,F(xiàn)(a(k))是一個(gè)基于裂紋長(zhǎng)度的非線性修正項(xiàng),非線性項(xiàng)U(smaxk-So(k))是單位階躍函數(shù),定義如下:

為了利用(1)式迭代計(jì)算裂紋長(zhǎng)度,開(kāi)裂壓力經(jīng)常由下面的一階差分方程給出:
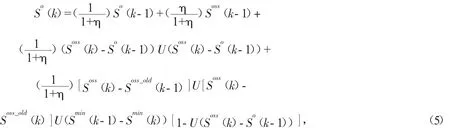
這里
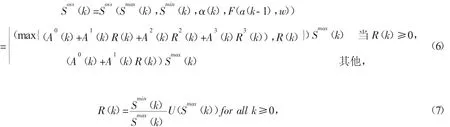
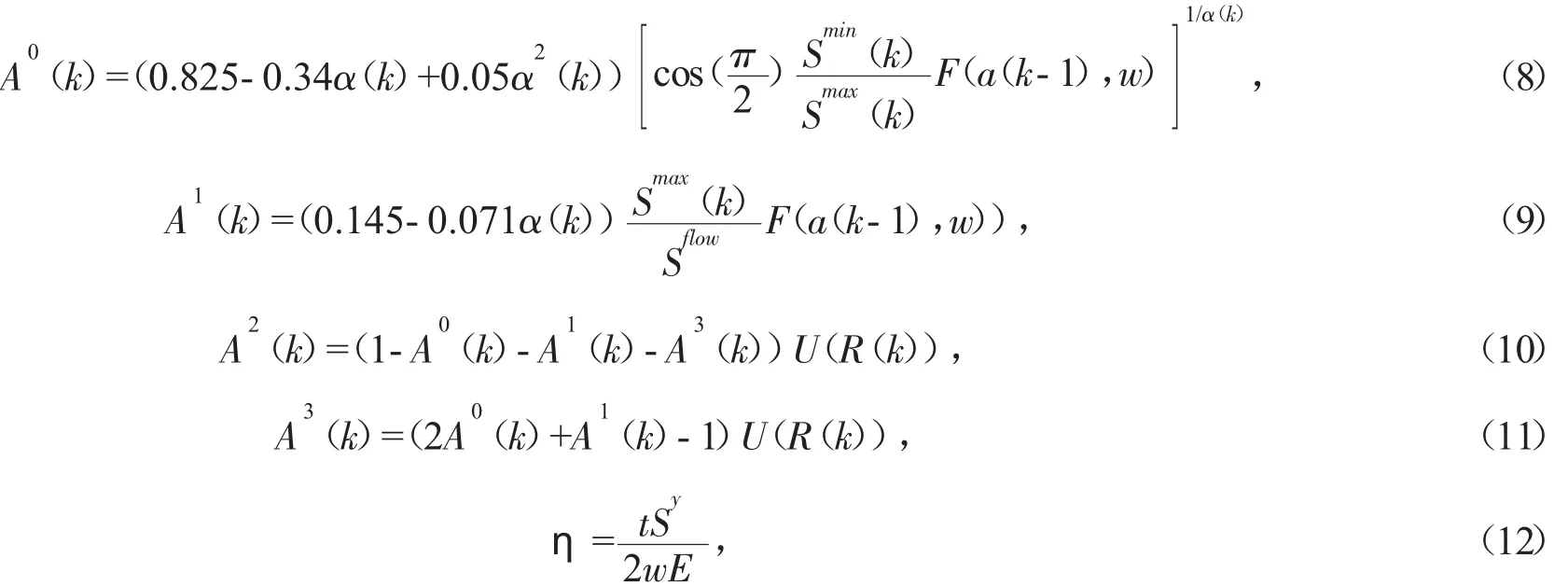
其中Sflow表示流變應(yīng)力,Sy表示彎曲強(qiáng)度,E表示楊式模量,t和w分別表示試件厚度和半寬度。
備注1 應(yīng)用(1)~(12)來(lái)計(jì)算裂紋長(zhǎng)度和開(kāi)裂壓力時(shí)存在的問(wèn)題:
1)(1)式中裂紋增長(zhǎng)模型和(5)式中的開(kāi)裂壓力模型都需要通過(guò)考慮材料特性、機(jī)械部件和裂紋表面的幾何特性來(lái)更新參數(shù),因此,通過(guò)這種迭代法求裂紋長(zhǎng)度和開(kāi)裂壓力是費(fèi)時(shí)的。
2)利用(1)來(lái)計(jì)算裂紋長(zhǎng)度在很大程度上依賴于式(5)~(12)中的開(kāi)裂壓力的計(jì)算。如果開(kāi)裂壓力測(cè)量不夠精確,準(zhǔn)確的裂紋長(zhǎng)度估計(jì)難以獲得。
3)非線性修正項(xiàng)F(a(k))的值是通過(guò)查表的方式來(lái)計(jì)算裂紋長(zhǎng)度和開(kāi)裂壓力的,但是預(yù)先準(zhǔn)備好的表不能適應(yīng)環(huán)境因素帶來(lái)的變化。
2 裂紋增長(zhǎng)過(guò)程的單隱層前饋神經(jīng)網(wǎng)絡(luò)建模
考慮到傳統(tǒng)的裂紋增長(zhǎng)模型所帶來(lái)的一系列問(wèn)題,在這篇文章中,我們將采用具有單隱層的前饋神經(jīng)網(wǎng)絡(luò)來(lái)建立裂紋增長(zhǎng)模型。與傳統(tǒng)的基于狀態(tài)空間的模型不同,我們將要建立的單隱層前饋神經(jīng)網(wǎng)絡(luò)模型是一種不依賴于狀態(tài)空間模型而只需要輸入輸出數(shù)據(jù)的模型。由于輸入輸出數(shù)據(jù)中包含了系統(tǒng)狀態(tài)的動(dòng)力學(xué)特征以及基于超限學(xué)習(xí)算法的單隱層神經(jīng)網(wǎng)絡(luò)的全局逼近能力,所要給出的模型能對(duì)裂紋增長(zhǎng)給出精確的估計(jì)。模型的結(jié)構(gòu)如圖1所示。這里,Smax(k)和Smin(k)分別表示最大和最小遠(yuǎn)程壓力,他們與各自的延時(shí)輸入序列D一起,構(gòu)成了網(wǎng)絡(luò)的輸入層。這里延時(shí)序列的存在反映了當(dāng)前輸出與歷史最大遠(yuǎn)程和最小遠(yuǎn)程壓力之間的動(dòng)力學(xué)關(guān)系。裂紋長(zhǎng)度ap(k)是模型的輸出。表示隱層節(jié)點(diǎn)的個(gè)數(shù),從圖上可以看到,這里只有單個(gè)隱層。wij(i=1,2,…,n;j=1,2,…,m)是網(wǎng)絡(luò)的內(nèi)權(quán),由于采取的是超限學(xué)習(xí)機(jī)算法,內(nèi)權(quán)的取值是在一定范圍內(nèi)隨機(jī)給定的。βi(i=1,2,…,m)是網(wǎng)絡(luò)的外權(quán),其值將通過(guò)批處理最小二乘法進(jìn)行估計(jì)。
下面具體給出圖1中各量之間的關(guān)系式。設(shè)輸入信號(hào)向量可表示為:
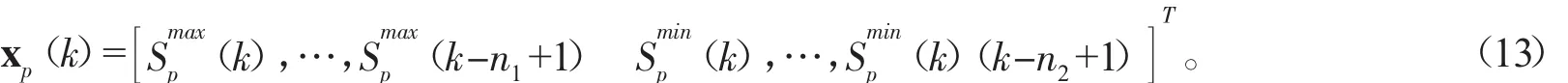
這里n1和n2分別表示最小和最大遠(yuǎn)程壓力的延時(shí)輸入的數(shù)目,且有n1+n2=n。輸入信號(hào)向量Xp(k)的下標(biāo)表示第p個(gè)輸入信號(hào)向量。在第p個(gè)輸入信號(hào)向量下,隱層節(jié)點(diǎn)的輸出可表示為:
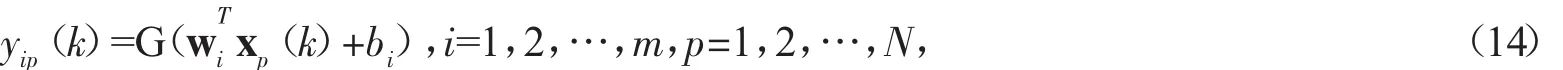
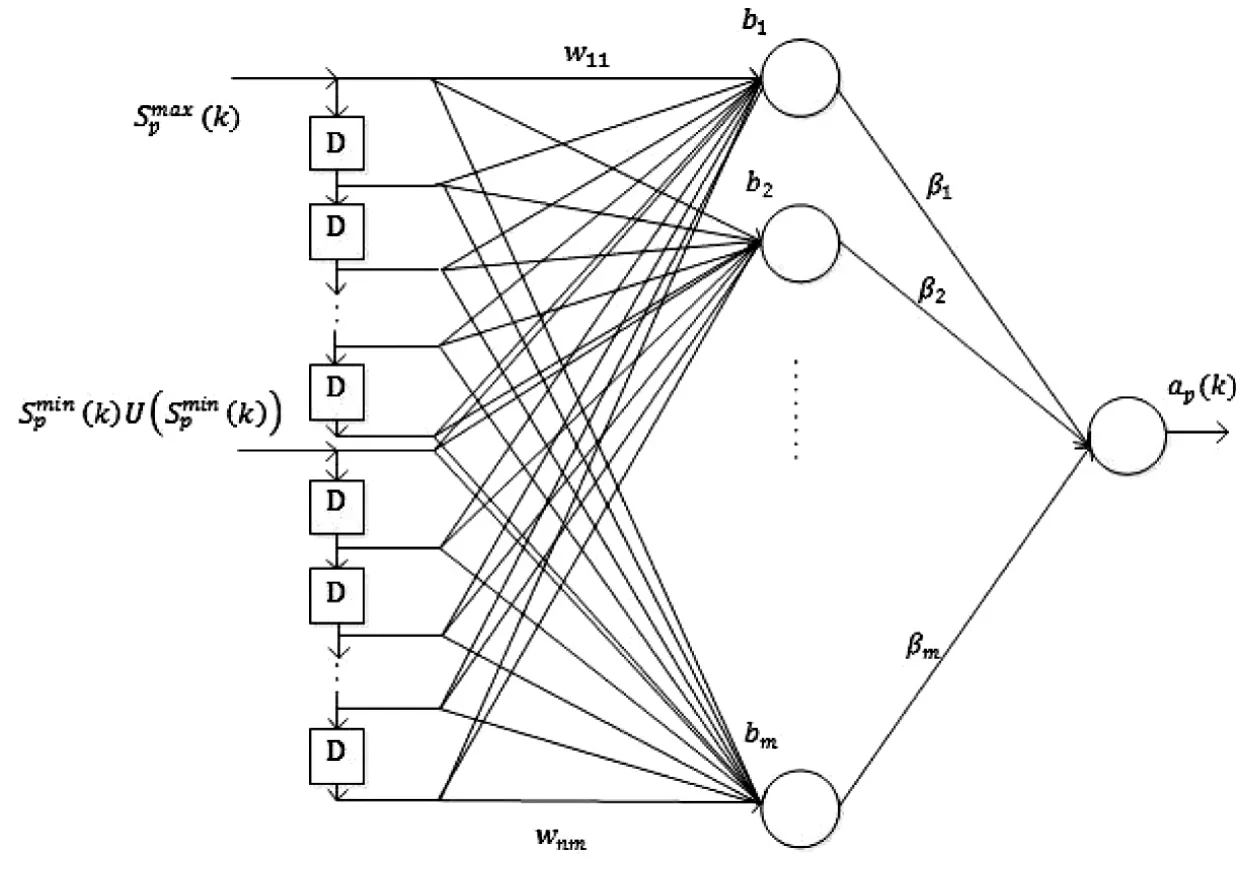
圖1 基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的裂紋增長(zhǎng)模型
其中bi表示第i個(gè)偏置,內(nèi)權(quán)向量可表示成

在第p個(gè)輸入信號(hào)向量下的網(wǎng)絡(luò)輸出可表示為

當(dāng)把所有的N個(gè)輸入信號(hào)向量全部輸入到神經(jīng)網(wǎng)絡(luò)中后,輸入輸出之間的關(guān)系可表示成以下矩陣形式

其中
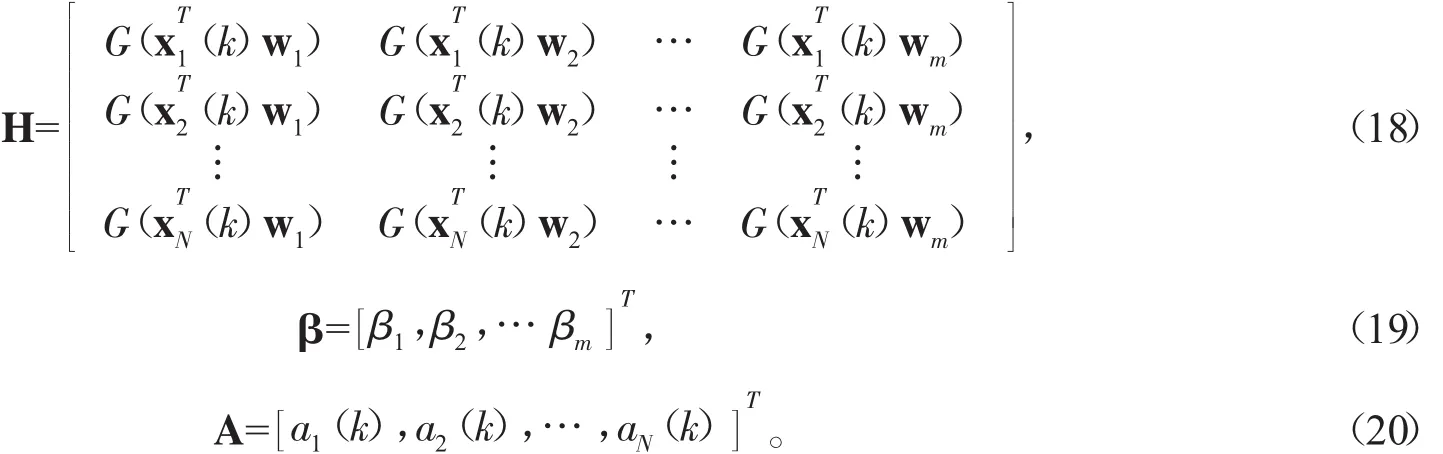
設(shè)期望的輸出向量可表示為

在式(17)中,令A(yù)=D,并利用最小二乘法,則最優(yōu)的外權(quán)估計(jì)可表示為

其中H+=(HTH)-1HT稱為矩稱H的Moore-Penrose廣義逆矩陣。
備注2 當(dāng)矩陣HTH存在奇異性時(shí),我們可利用正則化技術(shù)[6]去調(diào)整外權(quán)估計(jì)的表達(dá)式為:

其中r是取值為正數(shù)的正則化參數(shù)。
3 仿真結(jié)果
在仿真實(shí)驗(yàn)中,我們將用型號(hào)為2024-T351的鋁合金材料的實(shí)驗(yàn)數(shù)據(jù)來(lái)驗(yàn)證基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的裂紋增長(zhǎng)模型的有效性。實(shí)驗(yàn)數(shù)據(jù)來(lái)自于文[7],在溫度23℃的實(shí)驗(yàn)室環(huán)境中獲得。在仿真實(shí)驗(yàn)中,內(nèi)權(quán)在一定范圍內(nèi)隨機(jī)生成,偏置項(xiàng)采用白噪聲,隱層節(jié)點(diǎn)的個(gè)數(shù)n=15,正則化參數(shù)r=1 000。下面我們給出在兩種不同的壓力激發(fā)信號(hào)下的仿真結(jié)果。
如圖2所示,在第一個(gè)循環(huán)中加載最大為100 MPa和最小為-350 MPa的壓力后,接下來(lái)的循環(huán)中,最大壓力和最小壓力分別穩(wěn)定在59 MPa和29.5 MPa。為確保能捕捉到裂紋增長(zhǎng)的動(dòng)力學(xué)特性,我們采取50個(gè)循環(huán)采樣一次,并取前30次取樣數(shù)據(jù)來(lái)訓(xùn)練單隱層前饋神經(jīng)網(wǎng)絡(luò)的外權(quán)。如圖3所示,實(shí)線表示由實(shí)驗(yàn)數(shù)據(jù)所繪制的裂紋長(zhǎng)度曲線,虛線表示由神經(jīng)網(wǎng)絡(luò)輸出所繪制的裂紋長(zhǎng)度曲線。從圖中我們看出,用20%的實(shí)驗(yàn)數(shù)據(jù)所訓(xùn)練出來(lái)的外權(quán)能夠很好的預(yù)測(cè)接下來(lái)的從1 500~5 000個(gè)循環(huán)的裂紋長(zhǎng)度。圖4顯示了在第二種激發(fā)壓力下的情況。在第二次的仿真實(shí)驗(yàn)中,我們采取30個(gè)循環(huán)采樣一次,并取前30次取樣數(shù)據(jù)來(lái)訓(xùn)練單隱層前饋神經(jīng)網(wǎng)絡(luò)的外權(quán)。圖5顯示,在第二種激發(fā)壓力的情況下,單隱層前饋神經(jīng)網(wǎng)絡(luò)能很準(zhǔn)確的預(yù)測(cè)裂紋長(zhǎng)度。兩種仿真實(shí)驗(yàn)結(jié)果表明,基于單隱層前饋神經(jīng)網(wǎng)絡(luò)的裂紋增長(zhǎng)模型能在不同的激發(fā)壓力條件下有效地預(yù)測(cè)裂紋的變化趨勢(shì)。
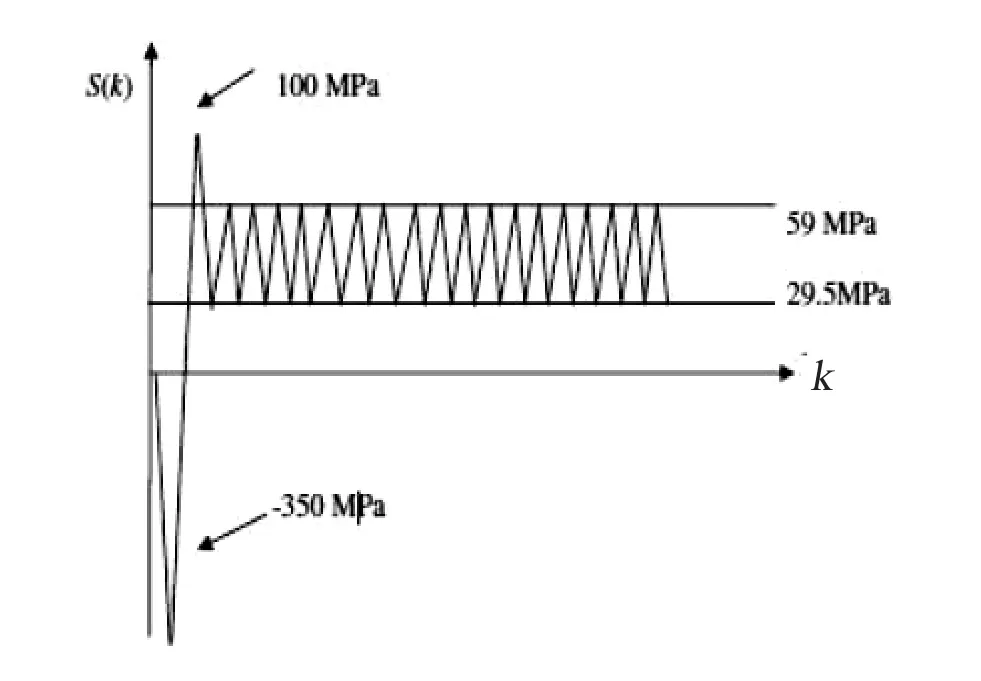
圖2 周期性激發(fā)壓力
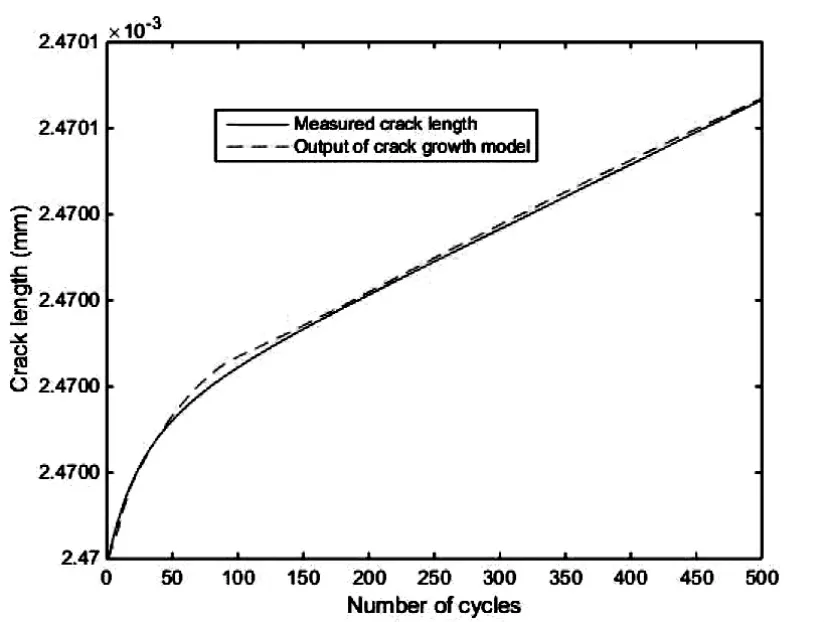
圖3 裂紋長(zhǎng)度測(cè)量值與估計(jì)
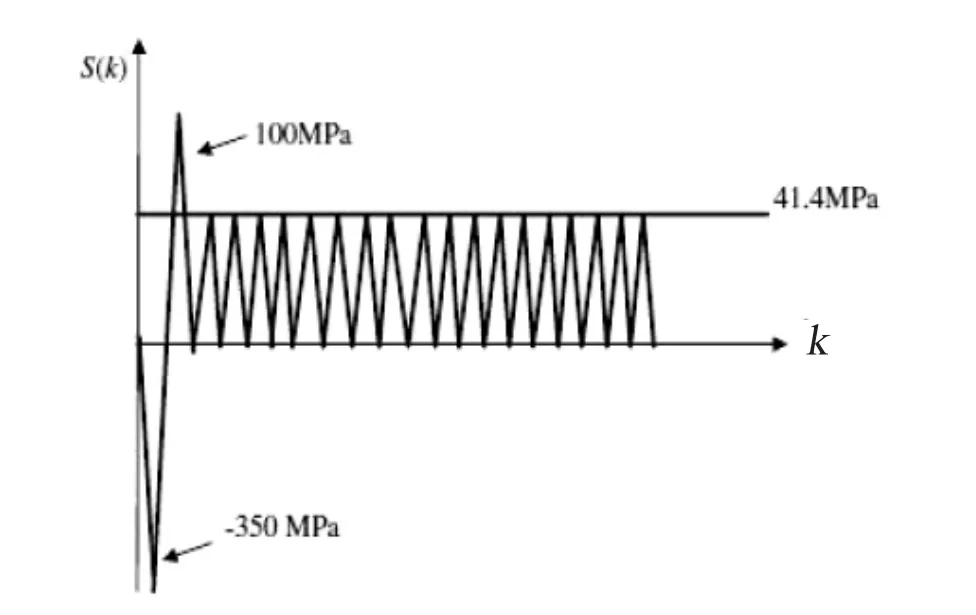
圖4 周期性激發(fā)壓力
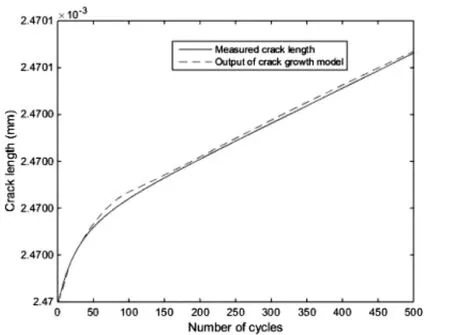
圖5 裂紋長(zhǎng)度測(cè)量值與估計(jì)值
4 結(jié)語(yǔ)
本文研究了如何運(yùn)用單隱層前饋神經(jīng)網(wǎng)絡(luò)來(lái)構(gòu)建裂紋增長(zhǎng)過(guò)程的模型,運(yùn)用了超限學(xué)習(xí)機(jī)算法,隨機(jī)在一定范圍內(nèi)給定內(nèi)權(quán),僅對(duì)外權(quán)利用批處理最小二乘法進(jìn)行全局優(yōu)化。仿真結(jié)果表明了所給出方法的有效性。
[1]PATANKAR R P,RAYA,LAKHTAKIAA.Astate-space model offatigue crack dynamics[J].International Journal ofFracture,1998,90(3):235.
[2]PATANKAR R,RAY A.State-space modelling of fatigue crack growth in ductile alloys [J].Engineering Fracture Mechanics,2000,66(2):129.
[3]RAY A,PATANKAR R.Fatigue crack growth under variable-amplitude loading:Part I Model formulation in state-space setting[J].Applied Mathematical Modelling,2001,25(11):979.
[4]RAY A,PATANKAR R.Fatigue crack growth under variable-amplitude loading:Part II– Code development and model validation[J].Applied Mathematical Modelling,2001,25(11):995.
[5]PATANKAR P,QU R.Validation of the state-space model of fatigue crack growth in ductile alloys under variable-amplitude load via comparison ofthe crack-openingstress data[J].International Journal ofFracture,2005,131(4):337.
[6]HAYKINS.Neural networks and learningmachines[M].NewJersey:Pearson Prentice Hall,2009.
[7]DABAYEH A,TOPPER T.Changes in crack-opening stress after underload and overload in 2024-T351 aluminium alloy[J].International Journal ofFatigue,1995,17(4):261.
Crack Gowth Process Diagnosis Based on Single-Layer Feedforward Neural Network
DUHong,YANGYi
(FacultyofEngineering,Lishui University,Lishui 323000,Zhejiang)
In this paper,a crack growth process diagnosis approach is proposed based on single-layer feedforwad neural network(SLFN).Firstly,we represent crack growth process through an input and output model with a single hidden layer.Then,we utilize the Extreme Learning Machine(ELM),which randomly selects input weights in a proper range and optimizes output weights via least square method,to train the nerual network.With this approach,the diagnosis and prediction of crack growth process can be achieved.
SLFN;ELM;crack length of alloy
10.3969/j.issn.2095-3801.2017.05.013
TP183
A
2095-3801(2017)05-0076-06
2017-05-08;
2017-06-19
浙江省教育廳科研項(xiàng)目“基于單隱層前饋神經(jīng)網(wǎng)絡(luò)模式識(shí)別的進(jìn)一步研究”(Y201432200)
杜鴻,男,浙江麗水人,講師,博士生。
- 麗水學(xué)院學(xué)報(bào)的其它文章
- 山區(qū)適用性信息技術(shù)人才培養(yǎng)的探析和實(shí)踐
- 卓越工程師培養(yǎng)質(zhì)量監(jiān)控體系的研究與實(shí)踐
——以麗水學(xué)院計(jì)算機(jī)科學(xué)與技術(shù)卓越工程師培養(yǎng)為例 - 生態(tài)資源開(kāi)發(fā)與利用虛擬仿真實(shí)驗(yàn)教學(xué)中心的建設(shè)與探索
- 基于方程駐軸的永磁同步電機(jī)動(dòng)態(tài)數(shù)學(xué)模型
- 啟閉機(jī)全虛擬仿真監(jiān)控平臺(tái)開(kāi)發(fā)
- 精益生產(chǎn)看板系統(tǒng)用SPI/CAN雙向數(shù)傳模塊的設(shè)計(jì)

