合理展開封頭曲面的研究

鄭鵬飛， 王 波， 趙菊娣， 林大鈞， 安 琦

(1.華東理工大學 機械與動力工程學院， 上海 200237；2.義烏工商職業技術學院 機電信息學院， 浙江 義烏 322000)

合理展開封頭曲面的研究

鄭鵬飛1， 2， 王 波2， 趙菊娣1， 林大鈞1， 安 琦1

(1.華東理工大學 機械與動力工程學院， 上海 200237；2.義烏工商職業技術學院 機電信息學院， 浙江 義烏 322000)

根據測地線的短程性與線上各點測地曲率為零的幾何特性，采用在不可展的封頭曲面上構建由測地線與法截線交織成線網的方法來獲得橢圓形封頭和球形封頭展開圖的邊界，并建立對應的數學模型，結合計算機編程，為參數化展開封頭曲面提供簡便、穩定可靠的方法.以曲面理論面積為評判標準，該方法展開精度高于工程上常用的幾種近似展開方法和CAD軟件的展開精度.

測地線； 封頭； 不可展曲面； 數學模型； 展開精度

在機械制造領域中經常會涉及曲面展開問題，特別是對不可展曲面的近似展開.不可展曲面的近似展開是航空航天、船舶制造和化工設備行業中的一項重要技術.國內外學者為此進行了廣泛研究，提出了各種曲面展開方法與技術[1-5]，如有限元法、幾何逼近法[6]、力學模型法[8-9]、能量方程法[11-12]、三維軟件法[7]、三角網格法[10，13]等.金玲等[6]利用AutoCAD對剛結構管構件進行曲面展開，但這類管構件屬于可展曲面，并未涉及不可展曲面的展開技術.黃鵬[7]利用CATIA軟件進行二次開發，對不可展曲面進行分割提取并展開.韓林等[8]利用彈簧-質點模型，將曲面三角化，以三角點作為質點，三角邊為彈簧，構建能量方程，計算質點的約束力，雖可進行曲面展開，但其計算過程較復雜，且計算量較大.現階段針對化工設備中的封頭曲面展開的相關研究較少.化工設備中橢圓形封頭和球形封頭的制造方法是將封頭曲面分成若干等分，利用畫法幾何原理在平板上展開各部分，然后模壓各塊展開的平板使之成為封頭曲面，再將模壓成型的各部分封頭曲面焊接成整體封頭.制造過程中如何在平板上展開封頭曲面，將直接影響成型封頭的形狀、精度及板材成本.

橢圓形封頭的幾何形狀為半個回轉橢球面，與球面一樣，均屬于不可展曲面.目前采用的幾種封頭曲面近似展開方法缺乏合理性.本文采用在不可展曲面上構建測地線和法截線線網的方法來展開橢圓形封頭和球形封頭，簡稱測法結合法，并選擇展開面積和理論面積之比作為評價標準，以評價其合理性.

1 建立數學模型

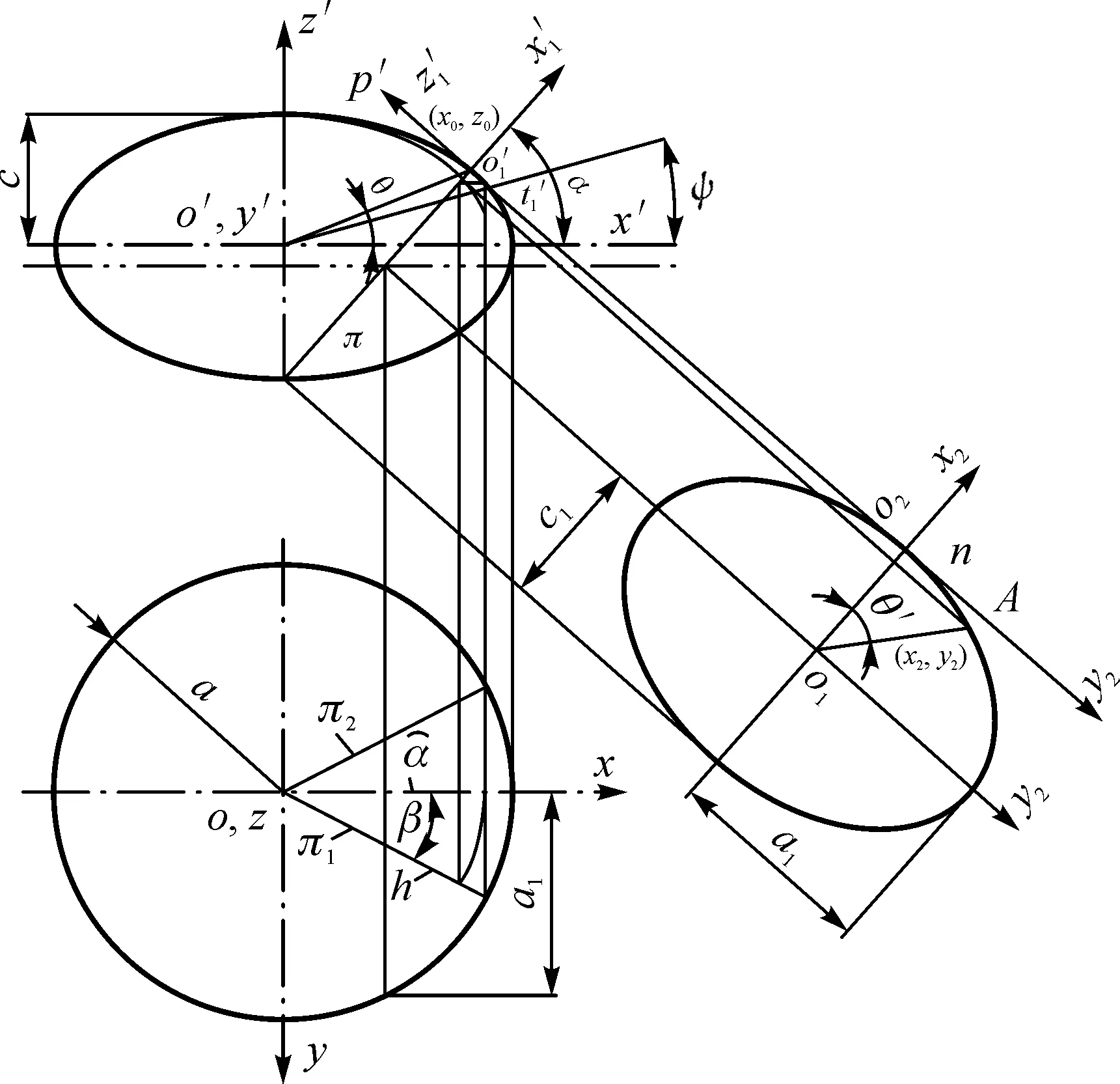
圖1 回轉橢球面展開圖解模型Fig.1 A flattening graphical model of ellipsoid

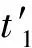
1.1測地線與法截線交點的確定

設o1點在oxyz坐標系中的坐標為o1(x0， 0，z0)，則有

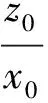
(1)

又o1點滿足

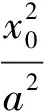
(2)

由(1)和(2)可得

(3)

圖1中坐標系o1x1y1z1與坐標系oxyz的轉換關系為

(4)

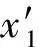
x1軸在oxyz坐標系中的斜率為

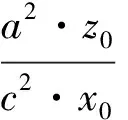
(5)

將式(1)代入式(5)中得

(6)

由此將式(3)和(6)代入式(4)中可得

(7)

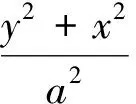
(8)

將式(7)代入式(8)中求解，可得當z1=0時o1x1y1z1平面與回轉橢球面的交線為G+E+F=1.

其中：

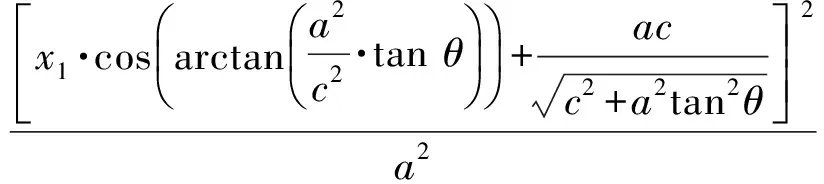
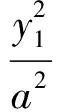
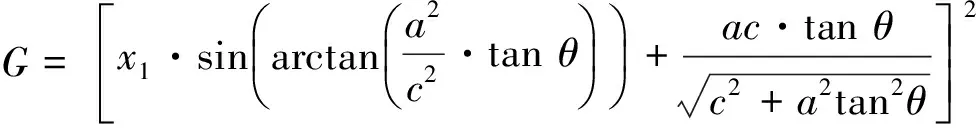
經整理得：

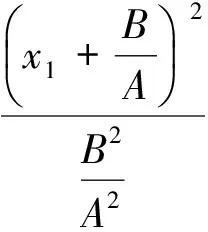
(9)

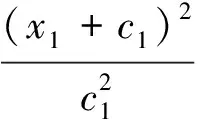
(10)

式(9)中A、B為

(11)

另外，鉛垂面π1與回轉橢球面的交線Ⅰ的方程為

(12)

正垂面π與回轉橢球面的交線Ⅱ的方程為

(13)

將式(1)、(3)與式(13)結合可得

(14)

則交線Ⅰ與交線Ⅱ的交點為

(15)

由式(15)可解出交點的x，y，z坐標值為

(16)

其中J(θ)，H(θ)，K(θ)為

(17)

1.2橢圓離心角

根據x，y，z可分別求出圖1中ψ與θ的函數關系以及θ與θ′的函數關系，下面分別述之

1.2.1ψ與θ的函數關系

由圖1可知

(18)

由式(18)可得

(19)

將式(16)中的x和z代入式(19)可得

(20)

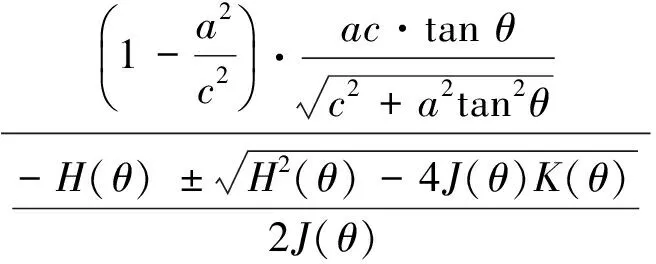
1.2.2θ與θ′的函數關系

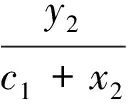
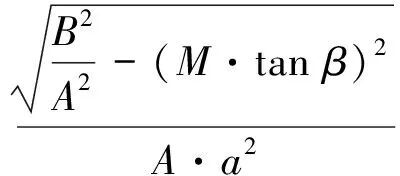
(21)

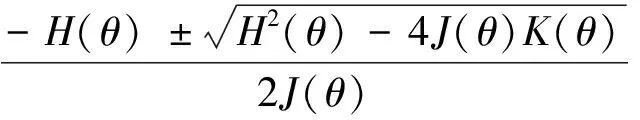
由此可得

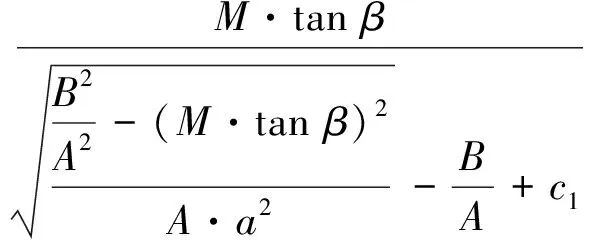
(22)

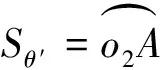
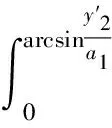
(23)

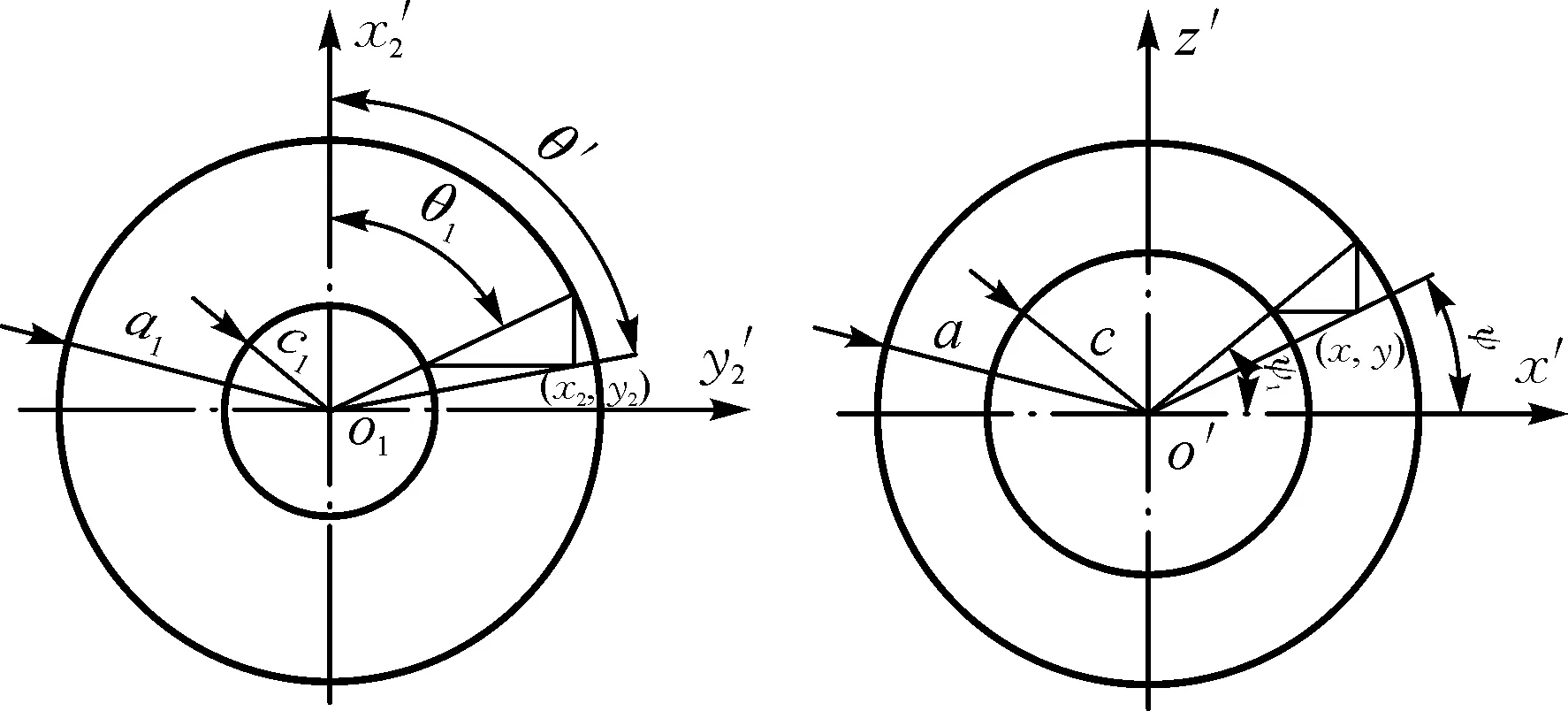
圖2 圓心角與離心角的關系Fig.2 Relationship between the center angle and centrifugal angle

1.3展開圖平面坐標系

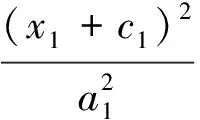
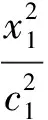
令x1=c1·sint，y1=a1·cost，則有

由此得Sθ ′弧上各點的曲率半徑為

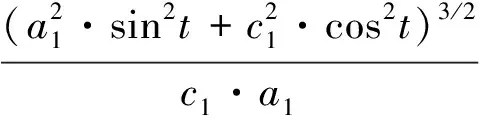
(24)

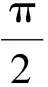
(25)

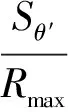
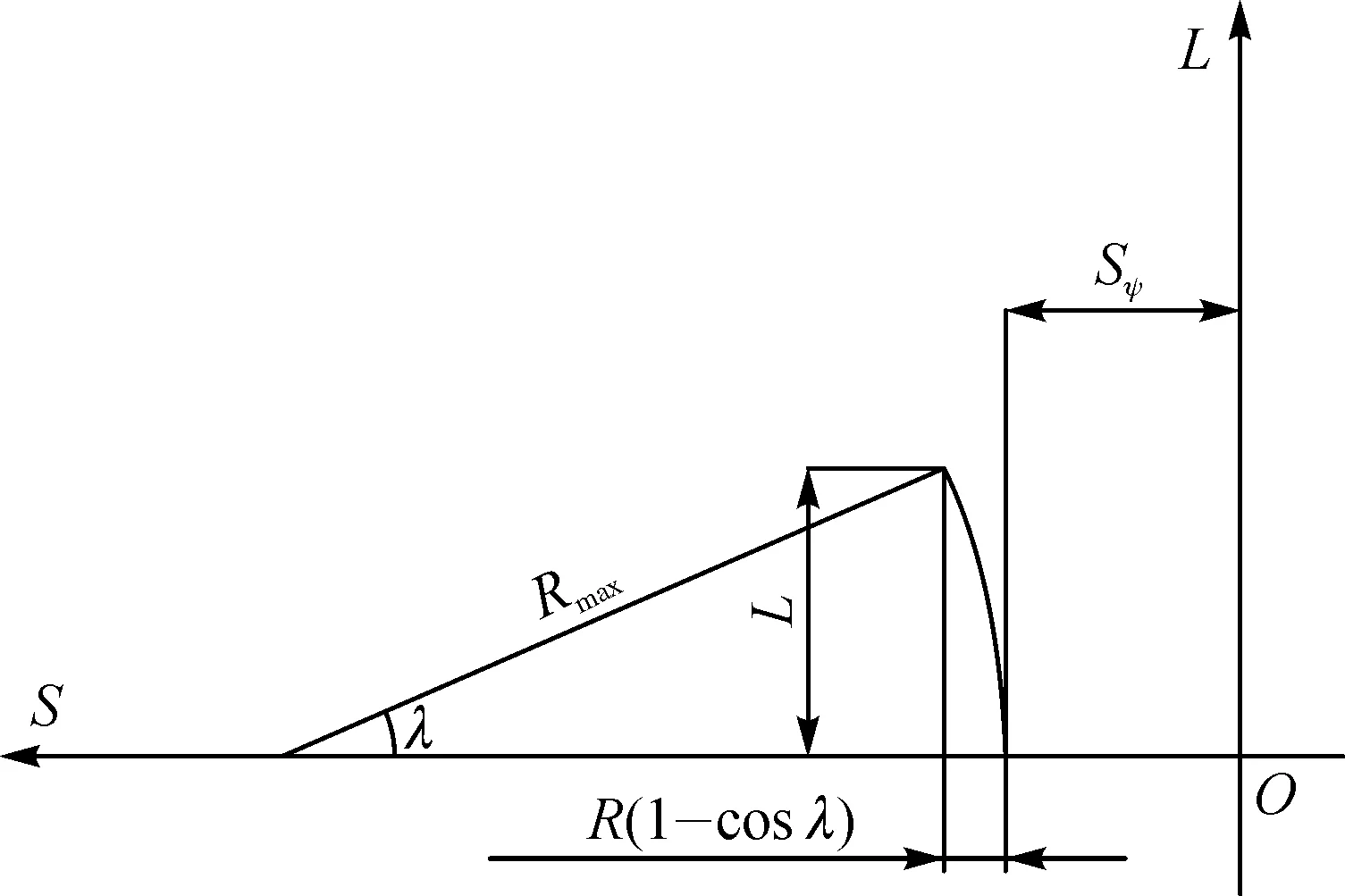
圖3 展開圖坐標系Fig.3 Coordinate system of flattening

式(25)即為橢圓形封頭曲面展開的數學模型，由該式可求得某一塊曲面展開邊界上各點的S和L坐標值，最后將所求得的一系列點光滑連接即得到一條展開曲線.以此方法可得到橢圓形封頭位于π1、π2兩平面之間曲面的展開圖.

2 算例驗證

因橢圓形(回轉橢球面)與球形(球面)均為不可展曲面，所以此類封頭制造中采用了各種近似的展開方法，包括CAD軟件.但理論上不可展的曲面不管用何種方法進行展開，客觀上均有誤差存在.以展開面積與理論面積之比作為評判標準，可用來鑒別各種展開方法的優劣.

2.1橢圓形、球形封頭的理論面積

球形封頭的理論面積計算過程較為簡單，可由球表面積計算公式得到.橢圓形封頭的理論面積A理論，則可根據回轉橢球面方程：r={a·cosφ·cosα1，a·cosφsinα1，c·sinφ}，由式(26)計算得到.

(26)

2.2測法結合法展開橢圓形、球形封頭的面積

為了驗證測法結合法的有效性，現對橢圓形封頭和球形封頭分別進行測試.橢圓形封頭：長半軸長為5 m，短半軸長為3 m，其理論表面積為117.368 m2；球形封頭：球半徑為R=5 m，其理論表面積(一半)為：157.080 m2.

根據上述橢圓形、球形封頭的尺寸，針對不同的β角度值，自動計算并繪制其展開效果圖，如圖4所示.表1列出了兩種封頭曲面的理論面積與展開面積的比較結果，可見本法精度高達99%.

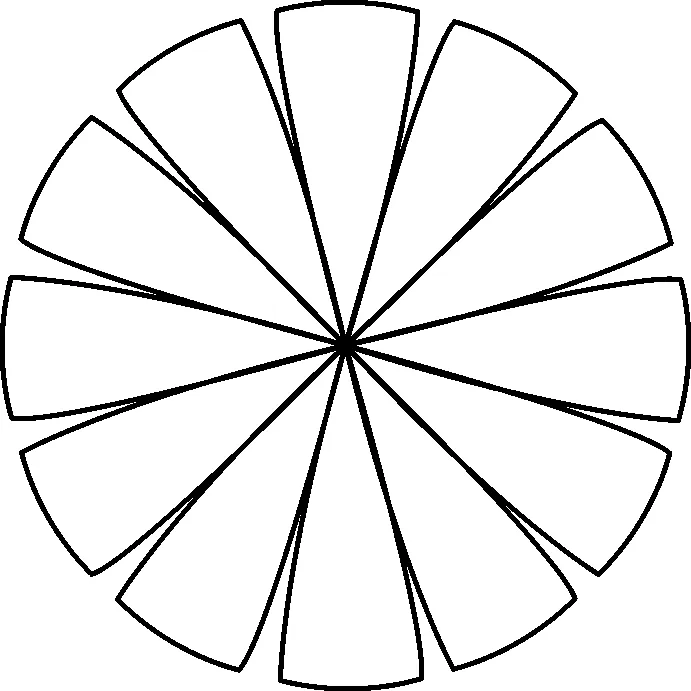
(a) 橢圓形

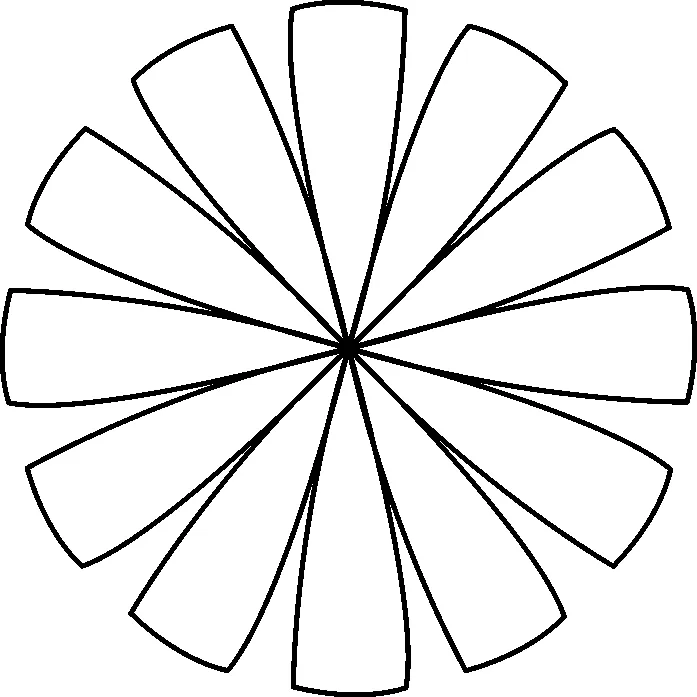
(b) 球形

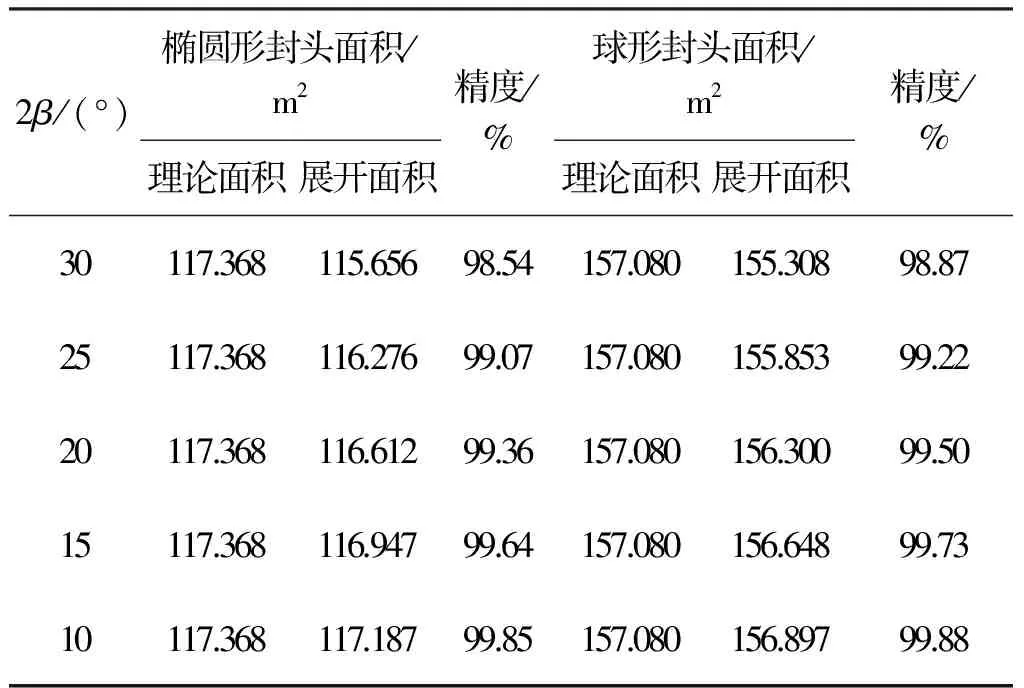
表1 橢圓形和球形封頭曲面展開面積誤差對比表

2.3各種展開方法的展開面積比較

以球形封頭為例，各種近似展開方法的展開面積誤差結果如表2所示.將球面分成12份，當R=1 250 mm 時，球面理論面積：A理論=19.635 m2.由表2可知，用測地線法展開的面積誤差最小(0.002 6%)，精度最高.

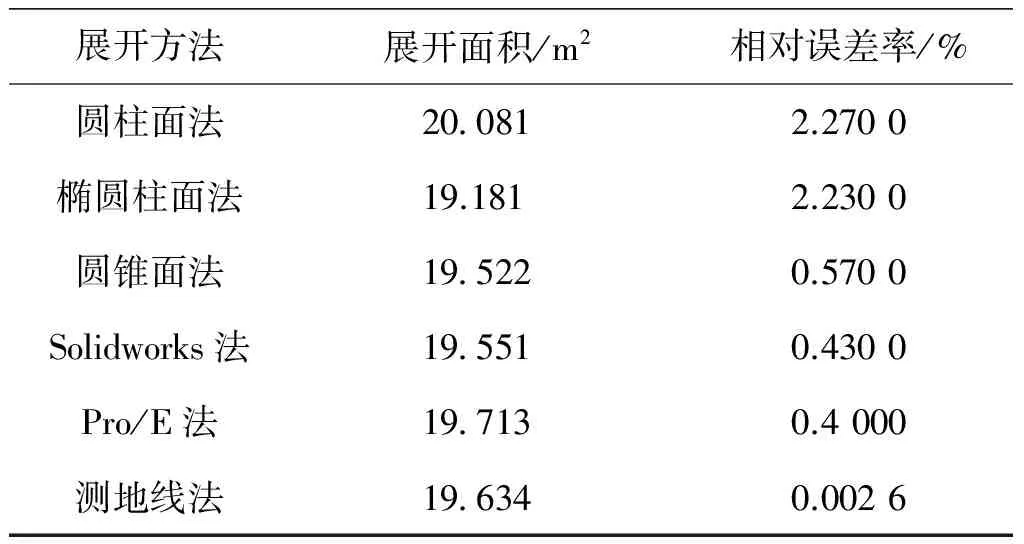
表2 不同展開法的面積誤差對比表

3 結 語

本文提出了一種通過在封頭曲面上構建測地線與法截線線網而進行曲面展開的幾何方法，并通過橢圓形封頭和球形封頭曲面展開算例驗證了該方法的正確性和精確性.此法也可拓展為測地線法在封頭曲面上建立全測地線網進行曲面的展開.因球面測地線比較簡單，并且本文篇幅有限，故文中未對球面的測地線網構建過程進行詳細描述，僅給出了結果以便與各種近似展開方法進行對比.

在封頭曲面上構建線網這一幾何模型是建立在曲面展開數學模型的基礎上.根據數學模型進行計算機參數化的曲面展開，本文提出了形、數、計算機結合解決問題的有效路徑.以封頭曲面的理論面積與展開面積之比作為評價各種近似展開方法優劣的標準，為判斷展開封頭曲面的合理性提供了技術參考.在后續的研究工作中，可考慮更多的曲面展開評價指標，如拼縫長度等，提出更多合理的自由曲面上的測地線計算、復雜不可展曲面的測地線展開法等.

[1] GAN M C， TAN S T， CHAN K W. Flattening developable bi-parametric surfaces[J]. Computers & Structures， 1996， 58(4)：703-708.

[2] ZHANG Q L， LUO X Q. Finite element method for developing arbitrary surfaces to fattened forms[J]. Finite Elements in Analysis and Design， 2003(39)：977-984.

[3] 張文俊，劉婷，張賢杰，等.整體壁板數字化展開建模方法[J].航空制造技術，2016，508(13)：56-61.

[4] 潘煒，吳慧，李鐵瑞，等.基于曲面展開的自由曲面網格劃分[J].浙江大學學報(工學版)，2016，50(10)：1973-1979.

[5] 崔曉坤，陳明.快速可展窄帶曲面設計[J].計算機應用研究，2012， 29(10)：3997-4000.

[6] 金玲，陳浩，張云飛.鋼結構設計中復雜曲面的計算機展開[J].上海應用技術學院學報(自然科學版)，2010，10(2)：97-100.

[7] 黃鵬.樣板設計中曲面展開問題及展開方法研究[J].航空制造技術，2014(S1)：155-157.

[8] 韓林，劉斌.基于彈簧-質點模型的三角網格曲面展開算法及其應用[J].華僑大學學報(自然科學版)，2011，32(6)：601-606.

[9] 梁堰波，徐偉辰，李吉剛，等.基于力學模型的曲面展開通用算法[J].計算機工程與設計，2012，33(9)：3539-3543.

[10] 詹雯，周來水，陳功.一種復雜曲面展開的通用算法[J].機械制造與自動化，2007，36(1)：83-87.

[11] WANG C C L， SMITH S S F， YUAN M M F. Surface flattening based on energy model[J].Computer-Aided Design， 2002，34(11)：823-833.

[12] 嚴國彪，劉斌.一種基于能量模型的曲面展開改進算法[J].華僑大學學報(自然科學版)，2011，32(2)：135-139.

[13] 陳功，周來水，安魯陵，等.一種通用的復雜曲面展開方法研究[J].中國機械工程，2007，18(24)：2914-2920.

(責任編輯：楊靜)

由表3可知：從檢出率上看，本文算法的檢出率相比模板匹配算法和分層檢測算法分別高出了15．80%和23．97%，達到97．32%；從平均耗時上看，本文算法比前兩種算法分別減少了24．30%和6．66%．不論從檢出率還是檢出速度上，本文算法均能滿足印刷工業的要求．

StudyonReasonableFlatteningofHeadSurface

ZHENGPengfei1， 2，WANGBo2，ZHAOJudi1，LINDajun1，ANQi1

(1.School of Mechanical and Power Engineering，East China University of Science and Technology，Shanghai 200237， China；2.School of Mechanical Information， Yiwu Industrial & Commercial College， Yiwu 322000， China)

According to the two geometric characteristics of geodesics that the path between two points is the shortest and the geodesic curvature at every point equals zero， the boundary of the flattening ellipsoidal head or spherical head is computed by weaving a mesh with geodesics and normal sections on the undevelopable head surface. A simple， stable， reliable and parameterized undevelopable surface flattening method is proposed， and the corresponding mathematical model is established by its computer programming. The theoretical area of surface is used as the criteria for evaluation. It can be seen from the experimental examples that the flattening accuracy of the method is higher than other usual methods and CAD software aided method.

geodesic； head； undevelopable surface； mathematical model； flattening accuracy

5 結 語

TP 391

A

1671-0444 (2017)04-0597-06

2017-01-05

鄭鵬飛(1984一)，男，浙江蘭溪人，講師，博士研究生，研究方向為CAD&CAGD.E-mail：pfzheng@126.com

安 琦(聯系人)，男，教授，E-mail：anqi@ecust.edu.cn