例析數學學習中的直覺思維培養

龐良緒

上海市市西中學 (200040)

例析數學學習中的直覺思維培養

龐良緒

上海市市西中學 (200040)

數學直覺思維是指人們不受固定的邏輯規則約束,對數學對象(結構及其關系)的某種直接領悟和洞察,它是人們運用已有的知識組塊和形象直感,對當前問題進行敏銳的觀察,細致的分析,透徹的理解,并能迅速發現解決問題的方向或途徑的一種思維形式.

作為科學探索能力，直覺顯然是十分重要的，這正如數學家龐加萊所指出的：“邏輯是證明的工具，而直覺則是發現的工具.” 那么，數學學習也需要直覺嗎？“一個懸而未決的難題，幾年來苦苦地在我腦海中反復盤旋.兩天之前我成功了……謎在一瞬間解開，像閃電一樣！我自己也說不清是什么導線，把我原先的知識和使我成功的東西連結了起來”.這是“數學王子”高斯在興奮地講述自己在一次重要突破中的體驗.這就是人類創造性思維中一朵神秘之花:靈感.身無彩鳳雙飛翼，心有靈犀一點通.龐加萊也指出：“直覺……對有創造性的科學家來說，是須臾不可缺的.”為此，加強數學直覺思維的培養，對培養學生的數學創造性思維是不可缺少的.

本文試從以下幾個方面探析數學直覺思維的培養.

1.追求美感，誘發直覺思維

數學教育的目的之一就是應該讓學生獲得對于數學美的鑒賞能力，這不僅有利于激發學生對數學的愛好，也有助于學生數學直覺思維能力的提高，感覺不到數學的美與優雅，就不會有數學直覺的產生，法國數學家阿達馬曾指出：發明就是選擇，而選擇則唯一地是由科學美感所支配的，數學直覺的本質是某種‘美感’或‘美的意識’，美的意識越強，發現和辯證隱蔽的和諧關系的直覺也就越強.

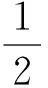
分析：觀察題目中條件與結論之間的結構后會發現：在a,b,c是任意值時等式是不成立的，從而在a,b,c之間存在比條件更簡潔的關系；作為特例考慮，顯然三個數有兩個數互為相反數時，條件與結論均成立，這意味著條件式子含有因式(a+b)或(a+c)或(b+c)，由于輪換對稱性，則必含有因式(a+b)·(a+c)·(b+c).于是數學直覺形成，只需化簡至既定目標即可推得結論.這個直覺來源于條件式子的輪換對稱美，和諧美.這也來源于對題目條件的直覺.

2.類比聯想，激發直覺思維

類比是根據兩個或兩個以上的對象之間某些方面的相似或相同，從而推斷出它們在其它方面的相似或相同的一種邏輯推理方法，數學模型方法是類比在數學中得到廣泛應用的一種形式，通過類比，迅速構建數學模型，將大腦中儲存的知識信息進行加工，形成思維組塊，從而啟迪思維，促使直覺產生.

案例4 求證:10092017>2017!.

這些解題中突然涌現出來的“靈機”，就是直覺的表現.相信每個數學學習者都希望自己多擁有一些這種才能.

應該指出，這種迅速識別、直接證明、綜合判斷的“數學洞察力”并非天生的，而恰恰是學習者數學素養的一種集中反映.扎實的數學基礎知識，靈活的變通思維能力，一定時間的冥思苦想加上適當的激發情境(如心情好，與別人進行研討，觸景生情等)，“直覺”也會垂青于你的.

請注意，別忘了記下自己產生“直覺”時的感受，因為，這還是一個值得深入研究的有趣的課題.

3.大膽猜想，構建直覺思維

猜想是一種合情推理，對于未給出結論的數學問題，猜想的形成有利于解題思路的正確誘導.對于已有結論的問題，猜想也是尋求解題思路策略的重要手段，數學猜想是有一定規律的，并且要以數學知識和經驗為支柱，而培養敢于猜想，善于探索的思維習慣是形成數學直覺，發展數學思維，獲得數學發現的基本素養.按照學生的認識發展規律，兒童階段的直覺思維在整個的思維活動過程中占有主導地位，但隨著年齡的增大，受到的挫折和傷害增多，直覺思維漸漸受到了抑制.事實上，直覺思維既容易由于受到鼓勵使之得到發展，也極易受到傷害而被扼殺，因此在教學活動中，要發展學生的直覺思維能力，就要鼓勵學生大膽猜想.

當然，直覺得到的結果也可能不完善，也可能是錯誤的，這時，還應與邏輯思維相結合，以導向正確的證明和演算.

案例6 曲線C:y=x2,有一條長為m的線段兩端在C上滑動,求它的中點縱坐標的最小值.

直覺繼續猜想,這條長度一定的線段兩端在拋物線上滑動,滑動…,它滑動時,中點坐標的改變只與直線的傾斜程度有關,可以用傾斜角作為中間變量.用分析思維驗證直覺猜想估計的結果:

4.觀察特征，引發直覺思維

直覺思維是把問題當作一個整體來分析，從全局出發，觀察其特征，避開具體細節的邏輯分析，直觀洞察，領悟本質，迅速產生解題思路.

案例7 已知x,y滿足x≥1,y≥1及(logax)2+(logay)2=loga(ax2)+loga(ay2) (a>0且a≠1)，當a∈(1,+∞)范圍內變化時，求loga(xy)的最值.

分析：由于已知條件的數量關系不夠明朗，觀察其結構特征，為使復雜的關系簡單化，直覺思維告訴我們采用換元法.

圖1

令s=logax,t=logay(s≥0,t≥0) ，題設條件轉化為(s-1)2+(t-1)2=4,(s≥0,t≥0)表示圓在第一象限內的一部分(如圖1).而所求loga(xy)=s+t，令s+t=k，則聯想為直線，k為截距.

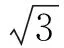
直覺思維是數學發現的關鍵因素,是邏輯的飛躍和升華,是人腦對數學對象及其結構敏銳的想象.直覺的領悟,迅速的判斷,是數學的洞察力.重視發展學生的數學直覺思維能力有利于創造型人才的培養，在數學教學中將直覺思維與邏輯思維有機地結合、相互補充，才能相映成趣、取得成效.至于怎樣培養自己的直覺能力，貝弗里奇提出過一些好的建議，諸如：對問題作長時間的思考，緊張思考后的“悠閑放松”，與別人交流，隨時記下思維的“閃光 ”……