2016年全國高中數學聯賽四川預賽15題的探究與推廣

劉 剛 趙 毅

北京市第十二中學 (100071)

2016年全國高中數學聯賽四川預賽15題的探究與推廣

劉 剛 趙 毅

北京市第十二中學 (100071)

1試題

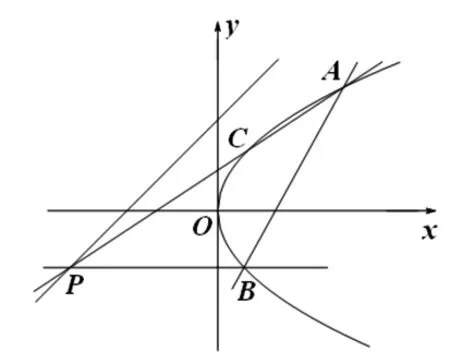
圖1

(2016年全國高中數學聯賽四川預賽)如圖1，已知拋物線y2=2px過定點C(1,2)，在拋物線上任取不同于點C的一點A，直線AC與直線y=x+3交于點P，過點P作x軸的平行線交拋物線于點B．

(1)求證：直線AB過定點；

(2)求△ABC面積的最小值．

試題考查了拋物線的標準方程、幾何性質、直線與拋物線的位置關系及定點、面積最值問題，考查了方程、轉化與化歸、分類與整合等數學思想以及坐標法的應用，檢驗了運算求解、分析問題與解決問題的能力．試題解法靈活，內涵豐富，是一道好題．

2解法探究

(1)問的探究

分析1:先設出A點坐標，求出直線AC的方程，與直線y=x+3的方程聯立得到P點坐標，然后根據直線PB與x軸平行求出點B的坐標，最后建立直線AB的方程從而得到答案．

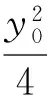
分析2:先設出直線AB的方程以及點A，B的坐標，然后根據直線PB與x軸平行表示出點P的坐標，利用A，P，C三點共線，由斜率建立等式關系，最后借助根系關系并消元得到一元一次方程，根據一元一次方程恒成立進行求解．

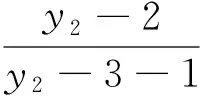
(2)問的探究

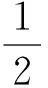
3推廣

經過對本題的深入研究，可得以下定理及推論．

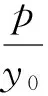
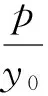
推論1 在拋物線y2=2px(p>0)上任取不同于頂點O的一點A，直線AO與直線x=a(a<0)交于點P，過點P作x軸的平行線交拋物線于點B，則直線AB過定點(-a,0)．

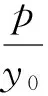
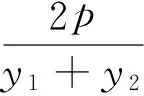
推論2 過定點Q(a,0)(a>0)的直線交拋物線y2=2px(p>0)于A，B兩點，過點B作x軸的平行線交直線AO(O為拋物線的頂點)于點P，點Q關于O的對稱點為M，則直線PM為x=-a．

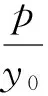
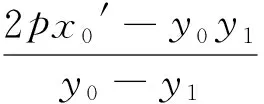
推論3 過定點Q(a,0)(a>0)的直線交拋物線y2=2px(p>0)于A，B兩點，直線AO與直線x=-a交于點P，則直線PB∥x軸．

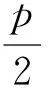
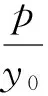
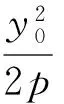
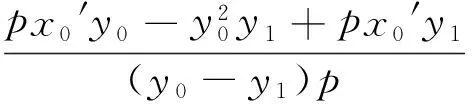
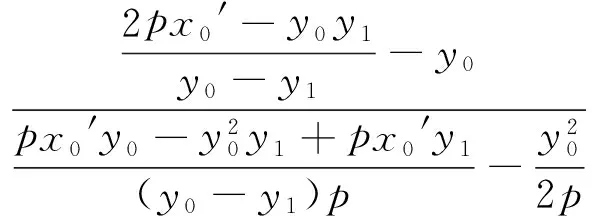
推論4 過定點Q(a,0)(a>0)的直線交拋物線y2=2px(p>0)于A，B兩點，過點B作x軸的平行線交直線x=-a于點P，則直線AP經過原點O．

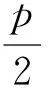
經過以上探究可以看出，這道競賽題是在課本及高考題的基礎上改編得來的．教材是集體智慧的結晶，對教學及各類考試有著導向作用，所以在習題教學中，要重視課本中的例習題，這樣可以最大化的提高教學效率．