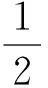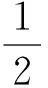從一道課本例題“證明+<2”說起
丁勝鋒
廣東省云浮市鄧發紀念中學 (527300)
丁勝鋒
廣東省云浮市鄧發紀念中學 (527300)

這是一道比較簡單的不等式的證明,教材的意圖是想通過這道題目來說明直接證明不容易,根據不等式的特點,尋求成立的充分條件,從而讓學生掌握分析法證明的基本思想和操作方法.我們很多老師在實際教學中也就是按照課本上的方式處理問題,然而,學生或多或少會產生疑問,這道題除了分析方法外,難道就沒有其它的方法?筆者從函數的觀點來證明不等式問題.


圖1

我們取x1=3,x2=7,也得到不等式的證明.
例若a,b∈R,且e 根據上述結論,我們可得到如下結論: 上述結論都是通過構造函數來解決不等式的問題,但如何恰當的構造函數,這需要根據題目本身的結構來構造,有時候我只需根據題目的原型結構來構造,有時候需要適當的變形,但具體選擇那種方式來構造,這需要根據題目本身來決定.下面我們通過一個例子來多角度的說明怎樣構造函數. (1)求a,b值;(2)證明:f(x)>1. 試題分析:試題(1)問不難,主要是考察導數的幾何意義,函數在一點處的切線方程,只要學生對切線概念充分理解并能準確求導,即可解決第(1)問.但第(2)問中函數不等式對大多數學生設置了門檻,這個門檻主要是導函數f′(x)的零點不好求,因此需要對函數不等式做適當的變形后再構造函數來處理. e-lnx≥e(-lnx)③,當且僅當-lnx=1時等號成立. (1)若g(x)與f(x)在同一點處有相同的極值,求實數a的值; (2)若對一切x∈(0,+∞),有不等式f(x)≥2xg(x)-x2+5x-3恒成立,求實數a的取值范圍; 因此關于不等式還是函數不等式的證明,我們可以通過題目本身的結構特點來構造函數,通過研究函數性質來加以證明.為我們提供了解決不等式的一個有力工具.但我們在構造函數時,又會出現構造的函數“好”“壞”直接影響解題成敗,一般來說,應盡可能的構造較為簡捷且很容易求出導函數零點的函數,要做到這一點,需要我們熟悉初等函數之間的組合. [1]吳振奎.中學數學證明方法[M].遼寧人民出版社,1985. [2]華中師范大學數學系.數學分析[M].高等教育出版社,2010. [3]王健.一道課本例題的多視角探究.中學數學教學參考,2016,8.