固定諧振荷載作用下曲線軌道動力響應特性研究

杜林林， 劉維寧， 劉衛(wèi)豐， 馬龍祥

(1. 北京交通大學 土木建筑工程學院， 北京 100044； 2. 西南交通大學 土木工程學院， 成都 610031)

固定諧振荷載作用下曲線軌道動力響應特性研究

杜林林1， 劉維寧1， 劉衛(wèi)豐1， 馬龍祥2

(1. 北京交通大學 土木建筑工程學院， 北京 100044； 2. 西南交通大學 土木工程學院， 成都 610031)

將曲線軌道視為周期性離散支撐結構，根據(jù)周期性結構的振動特性，通過引入移動荷載作用下曲線軌道梁的數(shù)學模態(tài)以及廣義波數(shù)，得出曲線軌道梁頻域響應的級數(shù)表達，進而求解固定諧振荷載作用下曲線軌道梁平面外彎扭耦合振動的響應特性。通過計算不同頻率固定諧振荷載作用下曲線軌梁的動力響應，可以求得曲線軌梁垂向位移頻響特性。對單層離散點支撐軌道模型進行計算分析可知：曲線軌道梁一階自振頻率受扣件支點垂向支撐剛度、垂向支撐阻尼系數(shù)、扣件支點間距變化影響較大，扣件支點垂向支撐剛度增加時軌梁一階自振頻率提高，垂向支撐阻尼系數(shù)增加時軌梁一階自振頻率略有減少，扣件支點間距減小時軌梁一階自振頻率提高；扣件支點間距對曲線軌梁頻響特性具有顯著的影響，跨中處一階pinned-pinned共振峰幅值及支點處反共振峰幅值隨支點間距的增加而變大；曲線半徑對地鐵軌道軌梁垂向位移頻響特性幾乎沒有影響。

曲線軌道；彎扭耦合；周期結構；頻響特性

曲線軌道能夠適應地形、地物、地質等條件的約束，滿足城市軌道交通線路的規(guī)劃設計要求[1]。然而列車通過曲線軌道時產(chǎn)生的振動問題卻不容忽視，以北京地鐵為例，曲線軌道處出現(xiàn)了大量的異常波磨，影響車輛運行甚至危及行車安全[2]，曲線段列車運行引起的地表振動響應較大[3]。不同于直線軌道，列車在曲線軌道運行時會引起曲線軌道的平面內振動以及平面外振動，對于列車運行時的垂向荷載來說，平面外振動占主要成分[4-5]，為研究列車通過曲線軌道過程中的輪軌相互作用關系，應首先明確曲線軌道的動力響應特性，因此需要研究固定簡諧荷載作用下曲線軌道彎扭耦合振動特性。

針對曲線梁振動特性的研究，姚玲森等[6]根據(jù)Vlasov[7]曲線梁平衡方程，采用傅里葉級數(shù)法求解簡支曲線梁內力，通過求解兩個聯(lián)立的四階微分方程得到曲梁的內力和變形。單德山[8]應用積分變換法，求解了移動荷載作用下簡支曲線梁彎扭耦合振動的解析解，并進一步研究了高速鐵路曲線梁橋車橋耦合振動。宋郁民等[9]運用模態(tài)疊加法，通過考慮列車曲線的通過特點及輪軌非線性相互作用，建立了空間列車-橋梁的耦合方程。Yang等[10]通過模態(tài)疊加法，研究了水平曲線簡支梁在豎向力和水平力的共同作用下，曲線梁的彎扭耦合振動響應。劉維寧等[11]根據(jù)曲線梁的傳遞矩陣，以Duhamel積分為基礎，推導了移動荷載作用下曲線Timoshenko梁平面外振動響應的解析解。總體來說，針對曲線梁振動特性的研究相對較少，固定諧振荷載作用下曲線軌道的動力響應問題仍需作進一步的研究。

不同于曲線車-軌動態(tài)耦合研究，曲線超高、輪軌間橫向相互作用力及軌底坡等對車軌動態(tài)相互作用影響較大[12]，本文主要研究固定簡諧荷載作用下曲線軌道的振動響應問題，可以忽略超高、橫向輪軌力、軌底坡等因素的影響，將曲線軌道簡化為周期性離散支撐的平面曲線梁。利用軌道結構周期性條件，將動力響應的求解映射于一個基本元之內進行，通過引入移動荷載作用下曲線軌道梁的數(shù)學模態(tài)以及廣義波數(shù)，得出了曲線軌道梁頻域響應的級數(shù)表達，進而求解得出軌梁的頻域動力響應，得到了固定諧振荷載作用下曲線軌道平面外彎扭耦合振動的響應特性。

1 曲線軌道梁動力響應分析

1.1 圓弧曲梁振動微分方程推導

在推導曲線梁振動微分方程時，假定曲線梁為等截面的勻質梁且曲率半徑為常數(shù)，橫截面具有豎直的對稱軸；曲線梁形心與剪切中心重合；曲率半徑遠大于橫截面、梁長的尺寸。曲線梁的坐標系按照右手螺旋法則規(guī)定，如圖1所示。

圖1 曲線梁坐標系Fig.1 Coordinate of curved beam

自由振動下，忽略高階微量，曲線Euler梁的軸向、徑向、垂向及扭轉振動微分方程為[13-15]

(1)

(2)

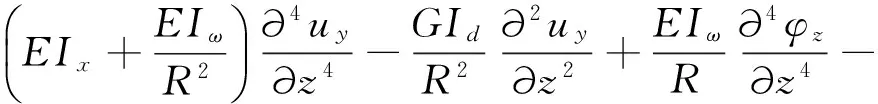
(3)

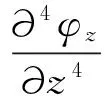
(4)

式中:uz、uy、uz分別為x、y、z方向上的位移；φz為繞z軸的扭轉變形；m為單位長度質量；ρ為密度；A為截面面積；Id為截面扭轉常數(shù)；I0為截面極慣性矩；E、G分別為曲線梁的彈性模量和剪切模量；Ix、Iy分別為繞x、y軸的截面慣性矩；Iω為截面扭轉翹曲常數(shù)；R為半徑。

由式(1)～(4)可知，式(1)～(2)表示曲梁的軸向及徑向，即平面內振動微分方程，式(3)～(4)表示曲梁的垂向及扭轉，即平面外振動微分方程。觀察式(1)～(4)可知，曲線梁平面內振動與平面外振動相互獨立，且曲梁平面內振動對平面外振動影響很小，因此，垂向荷載作用下曲線梁的動力響應僅考慮平面外振動情況。

考慮到曲線軌道曲線半徑遠大于軌梁截面尺寸，軌梁動力變形中可忽略翹曲扭轉，因而Iω=0，則曲線梁平面外自由振動微分方程為

(5)

(6)

1.2 曲線軌梁動力學控制方程

將鋼軌簡化為曲線Euler梁，將扣件簡化為彈簧阻尼支點，此時軌道簡化為等間距離散點支撐的軌梁模型，考慮一速度為v、角頻率為ωF的垂向單位移動諧振荷載eiωFt作用于軌梁上，如圖2所示。軌梁的振動微分方程可以寫為

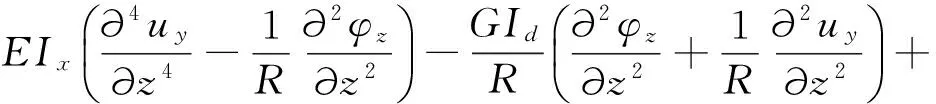
(7)

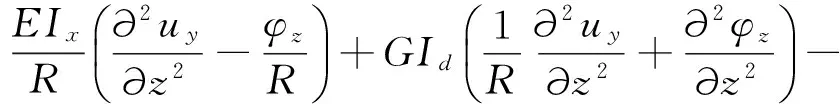
(8)

對式(7)、式(8)進行傅里葉變換

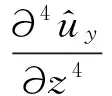
(9)

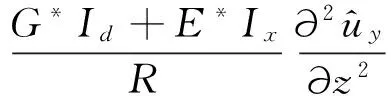
(10)

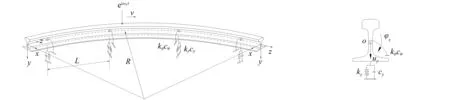
圖2 垂向移動簡諧荷載作用下曲線軌道梁力學模型圖3 軌梁變形及約束示意圖Fig2MechanicsmodelofcurvedtracksubjectedtoharmonicmovingloadsFig.3Schematicofconstraintofrail

1.3 曲線軌道軌梁頻域響應的廣義波數(shù)法

將曲線軌道映射至圓形軌道結構中[18]，根據(jù)周期性結構的性質對曲線軌道梁的動力特性進行分析，移動諧振荷載作用下軌梁頻域動力響應具有如下周期性性質[19]

(11)

式中:ω為角頻率；符號“＾”代表頻域內的物理量；L為軌梁的周期長度。

(12)

結合式(11)與式(12)，有

(13)

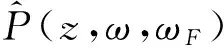
(14)

式中:Cn(ω,ωF)是傅里葉級數(shù)系數(shù)；ξn=2πn/L。

(15)

記：

(16)

(17)

(18)

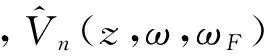
(19)

(20)

式中:2N+1為計算采用的軌梁模態(tài)數(shù)，記為NMR，即NMR=2N+1。

令：

κ=(ω-ωF)/v或ω=ωF+vκ

(21)

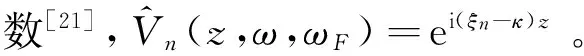
由軌梁頻域動力響應的模態(tài)疊加法可知：

(22)

(23)

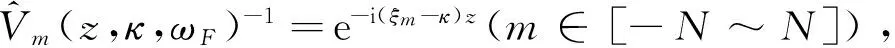
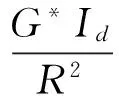
(24)

(25)

聯(lián)立式(24)及式(25)，整理可得：

G(κ,ωF)u(κ,ωF)=P(κ,ωF)

(26)

式中:u(κ,ωF)={U-N,…,U+N,Φ-N,…,Φ+N}T；G(κ,ωF)為(NMR+NMR)階方陣；P(κ,ωF)為(NMR+NMR)×1階已知向量，其第j行的值為

解式(26)可得：

(27)

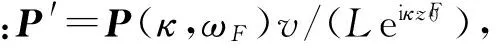
(28)

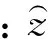
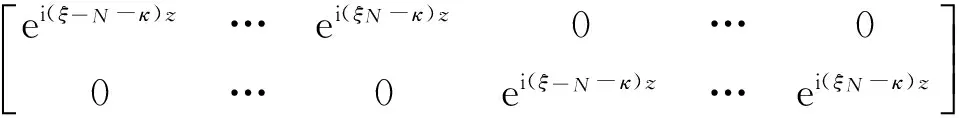
1.4 固定諧振荷載下曲線軌梁動力響應求解

根據(jù)已求出的軌道梁頻域響應，軌梁時域響應可采用逆傅里葉變換求得

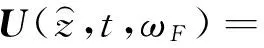
(29)

上式即為速度為v的移動諧振荷載作用下，軌梁時域位移響應解。令v=0，可得固定諧振荷載作用下軌梁的位移響應

(30)

式(30)表明：在固定諧振荷載作用下，軌梁穩(wěn)態(tài)響應是簡諧的，位移響應幅值為

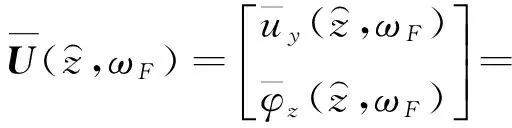
(31)

式(31)即為固定諧振荷載作用下曲線軌梁動力響應幅值，通過計算不同頻率固定諧振荷載作用下曲線軌梁的動力響應幅值，即可求得曲線軌梁垂向位移頻率響應函數(shù)。式(31)可采用數(shù)值積分法求解：

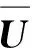
(32)

2 曲線軌道軌梁頻率響應函數(shù)分析

2.1 軌道梁模型及軌梁頻率響應函數(shù)計算

為求得曲線軌道梁垂向位移頻率響應函數(shù)，以北京地鐵普通整體道床軌道為例，軌道采用DTVI2扣件，軌道梁模型如圖4所示，以此模型研究曲線軌道動力響應特性，鋼軌及DTVI2扣件參數(shù)見表1。

根據(jù)計算分析可知，軌梁模態(tài)數(shù)取為21，κ取值范圍為[-10，10]，Δκ取值為0.039，計算結果已充分收斂，可保證計算精度。

為研究曲線軌梁垂向位移頻響特性，本文分別計算了扣件支點處及兩相鄰支點跨中處的頻率響應函數(shù)，其中激振點與拾振點布置如圖4所示，計算結果如圖5所示。

表1 T60鋼軌及DTVI2扣件參數(shù)Tab.1 Parameters of T60 rail and DTVI2 fasteners

支點處

跨中處圖4 不同位置處頻響函數(shù)布置圖Fig.4 Frequency response of track at different load points

圖5 軌梁支點及跨中處垂向位移頻響函數(shù)Fig.5 Frequency response of rail at a fastener support point and mid-span between fastener support points

2.2扣件支點垂向支撐剛度及阻尼系數(shù)對頻響函數(shù)的影響

為了研究支點垂向支撐剛度對軌梁垂向位移頻響函數(shù)的影響，本文分別計算了支點垂向支撐剛度為15 MN/m、30 MN/m、90 MN/m及120 MN/m時支點處和跨中處的頻響函數(shù)。為研究支點垂向支撐阻尼系數(shù)對頻響函數(shù)的影響，分別計算了垂向支撐阻尼系數(shù)為0.01 MN·s/m、0.04 MN·s/m及0.07 MN·s/m時支點處和跨中處的頻響函數(shù)。其余參數(shù)如表1所示。

圖6給出了不同支點垂向支撐剛度作用下跨中處及支點處的軌梁垂向位移頻響函數(shù)，觀察圖6可知：①曲線軌梁一階自振頻率受支點垂向支撐剛度變化影響較大，支點垂向支撐剛度的增加會引起軌梁一階自振頻率的提高，降低一階自振頻率點處的響應幅值，增加頻響函數(shù)在高于一階自振頻率頻段的幅值；②扣件支點垂向支撐剛度變化對離散點支撐軌梁一階pinned-pinned共振頻率沒有影響。

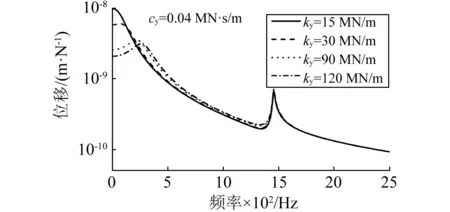
跨中處

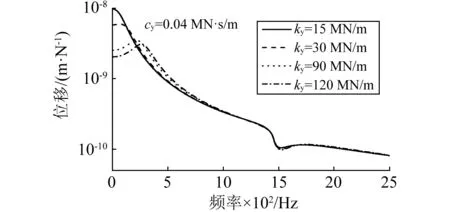
支點處圖6 垂向支撐剛度對垂向位移頻響函數(shù)的影響Fig.6 Frequency response of track with different stiffness of fastener support point

圖7給出了不同支點垂向支撐阻尼系數(shù)作用下跨中處及支點處的曲線軌梁垂向位移頻響函數(shù)，觀察圖7可知：

(1)曲線軌梁一階自振頻率受阻尼系數(shù)變化影響較大，增加阻尼系數(shù)時，軌梁一階自振頻率略有減少，頻響函數(shù)在一階自振頻率點附近處的響應幅值有所降低；

(2)阻尼系數(shù)變化對離散點支撐軌梁一階pinned-pinned共振頻率沒有影響，隨著阻尼系數(shù)的增加，跨中處一階pinned-pinned共振頻率處響應幅值增加，支點處反共振峰響應幅值降低。

跨中處

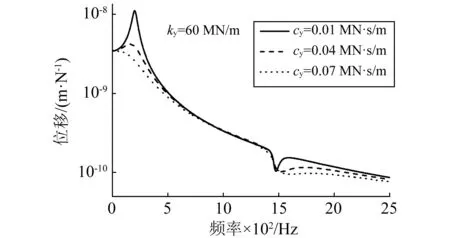
支點處圖7 垂向支撐阻尼系數(shù)對垂向位移頻響函數(shù)的影響Fig.7 Frequency response of track with different damping coefficients of fastener support point

2.3 曲線半徑及扣件間距對頻響函數(shù)的影響分析

為了研究曲線軌梁半徑及扣件支點間距對垂向位移頻響函數(shù)的影響，本文分別計算了曲線半徑為3 m、6 m、12 m、50 m、100 m、300 m、500 m及1 000 m時支點處和跨中處的頻響函數(shù)。為了研究扣件支點間距對軌梁垂向位移頻響函數(shù)的影響，本文分別計算分析了扣件支點間距為0.45 m、0.6 m、0.9 m及1.2 m時支點處和跨中處的頻響函數(shù)。其余參數(shù)如表1所示。

圖8給出了不同曲線半徑作用下跨中處及支點處的軌梁垂向位移頻響函數(shù)，由圖8可知：

(1)曲線軌道一階自振頻率幾乎不受半徑影響，半徑的增加對一階自振頻率沒有影響；

(2)在一階pinned-pinned共振點處，支點處共振頻率高于跨中處，曲線半徑與扣件間距比值小于10時，半徑對曲線軌道梁頻響函數(shù)具有顯著影響，隨著曲線半徑的增加，軌道梁一階pinned-pinned共振頻率變大，跨中處共振峰幅值降低，支點處反共振峰響應幅值提高；曲線半徑與扣件間距比值大于10時，隨著半徑的增加，半徑對曲線軌道梁頻響函數(shù)的影響逐漸降低，當半徑大于50 m之后半徑對曲線軌道梁垂向位移頻響函數(shù)幾乎沒有影響；

(3)地鐵曲線軌道最小半徑為300 m，隨著曲線半徑的增加，軌梁垂向位移頻響函數(shù)基本一致，半徑對曲線軌道垂向位移頻響函數(shù)幾乎沒有影響。

圖9所示為曲線半徑為300 m時，不同扣件支點間距下跨中處及支點處的軌梁垂向位移頻響函數(shù)。觀察圖9可知：

(1)扣件支點間距對曲線軌道一階自振頻率變化影響較大，支點間距減小時軌道一階自振頻率提高，一階自振頻率處響應幅值降低；

(2)根據(jù)計算公式求得支點間距為0.45 m、0.6 m、0.9 m及1.2 m時所對應的一階pinned-pinned共振頻率分別為2 563 Hz、1 442 Hz、640 Hz和360 Hz，與程序求解計算結果吻合良好，支點間距減小一半時，一階pinned-pinned共振頻率增大4倍；

(3)支點間距對曲線軌梁一階pinned-pinned共振響應具有顯著的影響，跨中處一階pinned-pinned共振峰幅值及支點處反共振峰幅值隨支點間距的增加而變大。

跨中處

支點處圖8 曲線軌道半徑對垂向位移頻響函數(shù)的影響Fig.8 Frequency response of track with different radiuses

跨中處

支點處圖9 扣件支點間距對垂向位移頻響函數(shù)的影響Fig.9 Frequency response of different spacing of fastener support points

3 結 論

本文將曲線軌道視為周期性離散點支撐結構，根據(jù)周期性結構的振動特性，通過引入移動簡諧荷載作用下曲線軌道軌梁的數(shù)學模態(tài)以及廣義波數(shù)，得出了垂向荷載作用下曲線軌道梁頻域響應的級數(shù)表達，進而求解得出垂向固定諧振荷載作用下曲線軌道梁平面外彎扭耦合振動的響應特性。通過計算不同頻率固定諧振荷載作用下曲線軌梁的動力響應，得到了曲線軌梁頻響特性。針對地鐵普遍采用的整體道床軌道，以單層離散點支撐軌道模型為基礎，通過計算分析扣件支點垂向支撐剛度、垂向支撐阻尼系數(shù)、曲線半徑及扣件支點間距對垂向位移頻響函數(shù)的影響，得到以下結論：

(1)曲線軌道軌梁一階自振頻率受支點垂向支撐剛度、垂向支撐阻尼系數(shù)、支點間距變化影響較大；支點垂向支撐剛度增加時軌梁一階自振頻率提高，一階自振頻率點處的響應幅值降低；垂向支撐阻尼系數(shù)增加時軌梁一階自振頻率略有減少，頻響函數(shù)在一階自振頻率點附近的響應幅值降低；支點間距減小時軌梁一階自振頻率提高，一階自振頻率點響應幅值降低。

(2)扣件支點垂向支撐剛度對軌梁一階pinned-pinned共振頻率沒有影響；增大垂向支撐阻尼系數(shù)時跨中處一階pinned-pinned共振峰幅值增加，支點處反共振峰幅值降低；扣件間距對軌梁一階pinned-pinned共振特性具有顯著的影響，跨中處一階pinned-pinned共振峰幅值及支點處反共振峰幅值隨支點間距的增加而變大；支點扣件間距減小一半時，一階pinned-pinned共振頻率增大4倍。

(3)地鐵軌道最小曲線半徑為300 m，隨著曲線半徑的增加，軌道垂向位移頻率響應函數(shù)基本一致，半徑對曲線軌道垂向位移頻響函數(shù)幾乎沒有影響。

[1] 顧保南, 姜曉明, 程曜彥,等. 論城市軌道交通最小曲線半徑標準的選擇[J]. 同濟大學學報(自然科學版), 2003(4): 428-431.

GU Baonan, JIANG Xiaoming, CHENG Yaoyan, et al. Study on radius standard of urban rail transit in China[J]. Journal of Tongji University (Natural Science), 2003(4): 428-431.

[2] 李克飛. 基于變速及曲線車軌耦合頻域解析模型的地鐵減振軌道動力特性研究[D]. 北京:北京交通大學, 2013.

[3] 袁揚. 地鐵列車振動環(huán)境響應預測的人工單點列脈沖激勵方法研究[D]. 北京:北京交通大學, 2014.

[4] 孫建鵬, 李青寧. 曲線箱梁橋地震反應的頻域精細傳遞矩陣法[J]. 地震工程與工程振動, 2009, 29(4): 139-146.

SUN Jianpeng, LI Qingning. Precise transfer matrix method for solving earthquake response of curved box bridges [J]. Earthquake Engineering and Engineering Dynamics, 2009, 29(4): 139-146.

[5] 魏雙科. 曲線梁橋的固有振動特性及地震反應分析[D]. 南京:南京工業(yè)大學, 2006.

[6] 姚玲森. 曲線梁[M]. 北京: 人民交通出版社，1989.

[7] VLASOV V Z. Thin-wall elastic beams[M]. Washington DC: National Science Foundation，1961.

[8] 單德山. 高速鐵路曲線梁橋車橋耦合振動分析及大跨度曲線梁橋設計研究[D]. 成都:西南交通大學, 1999.

[9] 宋郁民, 吳定俊, 侯永姣. 列車通過小半徑反向曲線橋梁的動力相互作用分析[J]. 工程力學, 2012(增刊1): 185-189.

SONG Yumin, WU Dingjun, HOU Yongjiao. Analysis of dynamics interaction about train curving bridge on small radius and reverse curve [J]. Engineering Mechanics, 2012(Sup1): 185-189.

[10] YANG Y B, WU C M, YAU J D. Dynamic response of a horizontally curved beam subjected to vertical and horizontal moving loads[J]. Journal of Sound and Vibration, 2001, 242(3): 519-537.

[11] 劉維寧, 李克飛, MARKINE V L. 移動荷載作用下曲線軌道振動響應解析解研究[J]. 土木工程學報, 2013(1): 133-140.

LIU Weining, LI Kefei, MARKINE V L. Analytical study on the vibration response of curved track structure subjected to moving loads [J]. China Civil Engineering Journal, 2013(1): 133-140.

[12] 王開云. 提速和高速鐵路曲線軌道輪軌動態(tài)相互作用性能匹配研究[D]. 成都： 西南交通大學, 2012.

[13] 孫廣華. 曲線梁橋計算[M]. 北京: 人民交通出版社,1995.

[14] 李惠生, 張羅溪. 曲線梁橋結構分析[M]. 北京: 中國鐵道出版社,1992.

[15] 漢斯 C P. 結構桿件的彎曲與扭轉[M]. 吳紹本，常嶺，譯. 北京: 人民交通出版社,1981.

[16] 翟婉明. 車輛-軌道耦合動力學[M]. 北京:科學出版社,2015.

[17] NAIR S, GARG V K, LAI Y S. Dynamic stability of a curved rail under a moving load [J]. Applied Mathematical Modelling, 1985,9(3): 220-224.

[19] BELOTSERKOVSKIY P M. Forced oscillations of infinite periodic structures [J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 1998: 85-103.

[20] 馬龍祥, 劉維寧, 李克飛. 移動荷載作用下浮置板軌道振動響應的頻域快速數(shù)值算法[J]. 鐵道學報, 2014(2): 86-94.

MA Longxiang, LIU Weining, LI Kefei. Fast numerical algorithm of floating slab track vibration response under moving loads in the frequency domain [J]. Journal of the China Railway Society, 2014(2): 86-94.

[21] 馬龍祥. 基于無限-周期結構理論的車軌耦合及隧道-地層振動響應分析模型研究[D]. 北京:北京交通大學, 2015.

Astudyoncurvedtrackdynamicresponseunderafixedharmonicload

DU Linlin1, LIU Weining1, LIU Weifeng1, MA Longxiang2

(1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China; 2.School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Modelling the dynamic behavior of a curved railway track subjected to fixed harmonic loads is important to understand its dynamic characteristics. The discretely supported curved Euler Beam was used to simulate dynamic response of curved track based on a periodic structure. Mathematical modes of track and generalized wavenumber were introduced, and dynamic response of bending and torsion of curved track in frequency domain was expressed by series superposition of the mathematical modes. Dynamic response of curved track subjected to a fixed harmonic load was obtained, and some conclusions were obtained. The natural vibration frequency of curved beam was greatly affected by vertical stiffness, vertical damping coefficient and spacing of fasteners. The first-order natural frequency of track increased with increasing the vertical stiffness of fastener, but decreased slightly with increasing the vertical damping of fastener. The first-order natural frequency of track increasing as the fastener spacing is decreased. Fastener spacing has a significant influence on response of curved track. The bigger the fastener spacing, the greater the amplitude of first order pinned-pinned resonance in mid-span and the bigger the amplitude of first order pinned-pinned anti-resonance in fastener support. Radius has little effect on vertical displacement frequency response of a curved track in metro.

curved track; coupling of bending and torsion; modal superposition method; periodical structure; frequency response function

國家自然科學基金項目(51378001)；中央高校基本科研業(yè)務費專項資金資助項目(2015YJS122)

2016-10-19 修改稿收到日期： 2016-12-18

杜林林 男，博士生，1988年生

劉衛(wèi)豐 男，博士，副教授，博士生導師，1975年生

U213.2

A

10.13465/j.cnki.jvs.2017.20.035