沖擊振動單邊單質量破碎系統的非線性動力學分析

倪素環，楊 雪

(河北科技大學機械工程學院，河北石家莊 050018)

1008-1542(2017)05-0469-05

10.7535/hbkd.2017yx05009

沖擊振動單邊單質量破碎系統的非線性動力學分析

倪素環，楊 雪

(河北科技大學機械工程學院，河北石家莊 050018)

為研究和開發高效振動式破碎機，針對所研究的沖擊振動破碎系統建立單邊動力學模型，利用牛頓定律建立振動微分方程，進行動力學分析。通過作出幅頻曲線、滯回沖擊力曲線、能量吸收曲線，分析其對系統響應的影響。利用所得結論用數值分析法解出此系統受迫主共振，求得位移、速度及加速度的時間歷程，說明質量塊的運動并非簡單的簡諧運動，非線性沖擊力是振動系統中影響較大的一個因素；得到間隙、激振頻率對幅頻曲線、沖擊力和能量吸收的影響規律。研究表明，物料與破碎頭之間的間隙值應盡量小，以用更小的激振力達到更好的破碎效果，且系統工作在主共振區時可獲得大的沖擊力。研究結果為深入分析振動系統的規律及機制提供了參考。

礦石處理；單邊單質量；幅頻；沖擊力；能量吸收；動力學

所謂振動破碎是指由相對振動的2個剛體，對其間的顆粒層加以高頻沖擊，使層間發生破碎[21]。如圖1所示破碎機具有6個自由度，是一個具備剛體復雜運動的振動系統，此系統同時具有強非線性剛-散耦合特性[1-7]。在此振動系統中，研究剛-散耦合效應，勢必對其規律及機制進行深入的研究分析。故首先研究沖擊振動系統中單邊單質量系統。

1 建立動力學模型

對圖1所示的破碎系統建立動力學模型，2個偏心距為e的相同偏心塊(質量分別為m0/2)連接在彈性梁上，每個電機驅動1個偏心塊，讓2臺電機以相同的角速度ω反方向轉動，產生的離心力為m0eω2sin(ωt)，則系統產生圖2所示x方向的強迫振動，位于偏心塊下部的沖擊破碎頭會撞擊物料槽中的物體使其破碎。如圖2所示為其動力學模型，比例阻尼c和線性彈簧k與質量塊m三者相連，系統在激振力m0eω2sin(ωt)的作用下做強迫振動，當x大于σ時，質量塊就會撞擊物料，使其破碎。假設在振動過程中，彈簧產生線性恢復力，物料產生沖擊恢復力，而該沖擊恢復力以一種非線性、非光滑形式出現[2]。

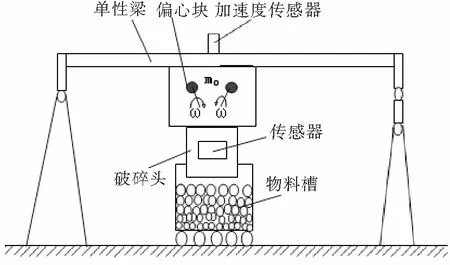
圖1 沖擊振動單質量破碎系統Fig.1 Single mass vibration impacting crashing system

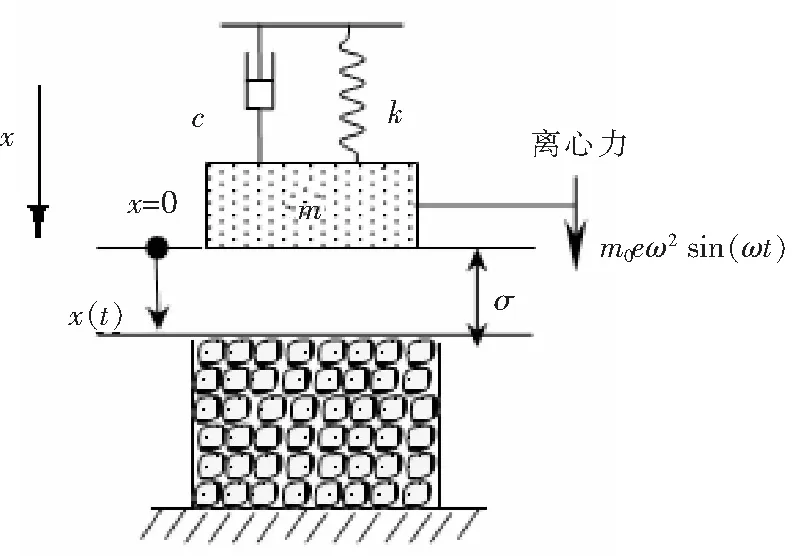
圖2 動力學模型Fig.2 Dynamic model

2 振動微分方程

首先建立坐標系，坐標原點為靜平衡位置，橫坐標為x，向下為正，如式(1)所示，利用牛頓定律建立振動微分方程。

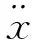
其中

式(1)可規范為

首先要將二階微分方程化為狀態方程形式，引入狀態變量：

狀態變量y1和y2分別代表質量塊的絕對位移和絕對速度，因而可以寫出狀態方程組如式(4)所示。

分段表示的系統狀態方程如下。

1)當y1≥σ且y2≥0時

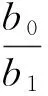
3)當y1<σ時

給定系統參數，選擇合適的步長，就可以利用Runge-Kutta法對系統進行數值分析[9-11]。

3 動力學分析

設式(1)中的參數為

m=135 kg,m0=17.57 kg,e=0.032 6 m,k=2.115 31×105N/m,ξ=0.06，a4=8.378 7×1011,a3=-0.151 4×1011,a2=0.001 9×1011,a1=0.0,a0=0.0,b1=5.606 5×107,b0=-0.107 9×107。

針對式(1)用榮格庫塔(Runge-Kutta)4階法進行數值求解，研究此系統運動的規律。

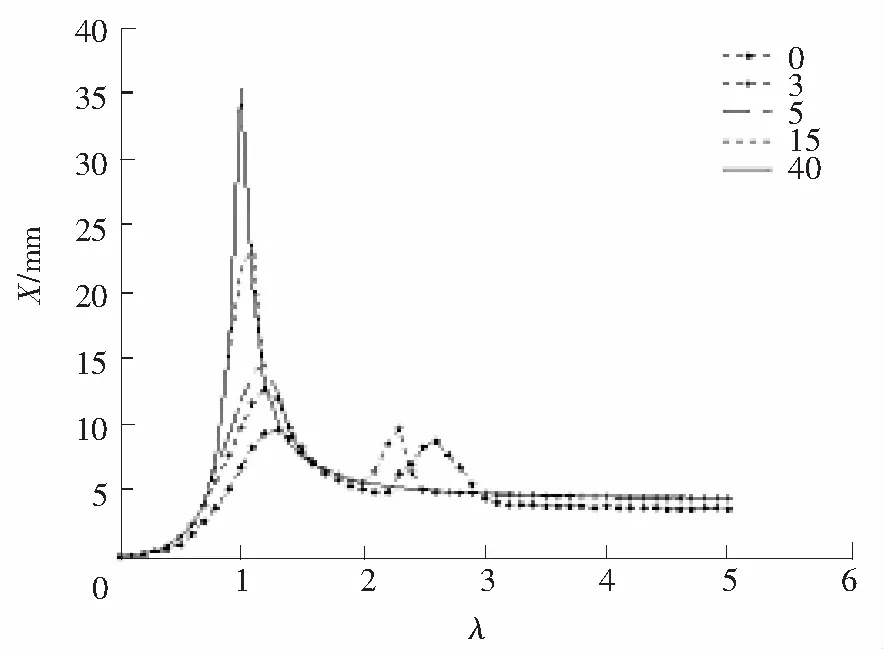
圖3 幅頻曲線Fig.3 Amplitude frequency diagram

3.1 影響系統響應的間隙、頻率比

3.1.1 幅頻曲線

作不同間隙值σ的幅頻曲線，如圖3所示(頻率比λ為橫坐標，振幅X為縱坐標)。通過計算得知，當破碎系統中沒有物料時，系統的振幅為35 mm,所以當σ≥35 mm時，質量塊不會與物料產生接觸，系統的振動就不會受到系統內物料的影響。由圖3可知：

1)系統的主共振頻率與物料的間隙量密切相關，間隙量越小，主共振頻率就越大。

2)系統在σ=0～3.2 mm的范圍內，只產生了1/2次亞諧共振，沒有出現其他亞諧共振。

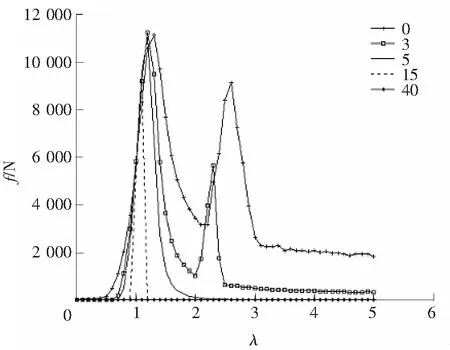
圖4 沖擊力曲線Fig.4 Wallop diagram

3)系統的主共振幅值與物料的間隙量也密切相關，間隙愈小，系統的振動幅值愈小。

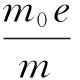
3.1.2 沖擊力曲線

如圖4所示為不同間隙值σ下的沖擊力曲線(頻率比λ為橫坐標，沖擊力的最大值f為縱坐標)。

由圖4可知：

1)當間隙不變時，沖擊力在主共振點達到最大值，越過主共振點，沖擊力迅速減小；沖擊力在1/2次亞諧共振點再次達到峰值。故在主共振點或亞諧共振點沖擊力較大。

2)當頻率比不變時，沖擊力隨間隙的增大而減小，直至趨于零。

3)沖擊力存在的頻率范圍受間隙影響，間隙越小，頻率范圍越大。

所以，物料與破碎頭之間的間隙要小，才能用小的激振力達到好的破碎效果，且系統最好在主共振區或亞諧共振區工作以獲得大的沖擊力。

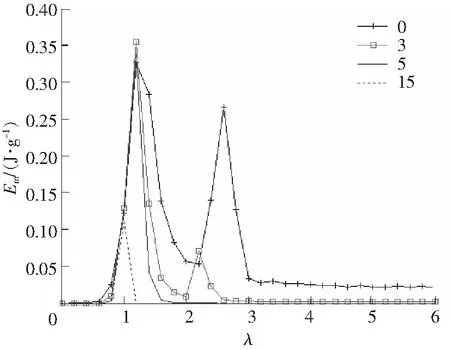
圖5 能量吸收曲線Fig.5 Energy absorbing diagram

3.1.3 能量吸收曲線

破碎效果最重要的因素是能量吸收，作不同間隙值σ的能量吸收曲線，如圖5所示(頻率比λ為橫坐標，能量吸收E為縱坐標)。由圖5可知：

1)能量吸收的效果受間隙影響，間隙愈小，能量吸收反而愈大。

2)能量吸收在主共振時最大，亞諧共振時較小。

3)在主共振時物料每個周期被沖擊1次，在1/2次亞諧共振時物料每2個周期被沖擊1次，由此可知，在相同時間內，能量吸收在主共振點時最大。

3.2 系統的受迫主共振

分析間隙為零的情況，從圖3的幅頻曲線得出，當σ=0時，共振頻率比λ=1.3，用數值仿真法對系統的共振情況進行分析，得到位移、速度和加速度的時間歷程圖，如圖6—圖8所示。

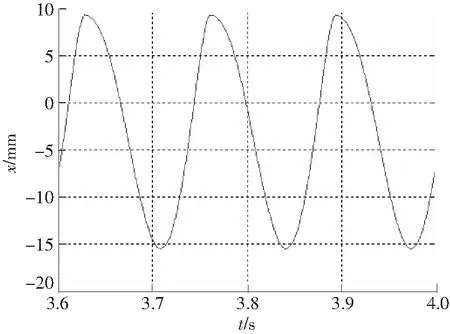
圖6 位移歷程Fig.6 Displacement course

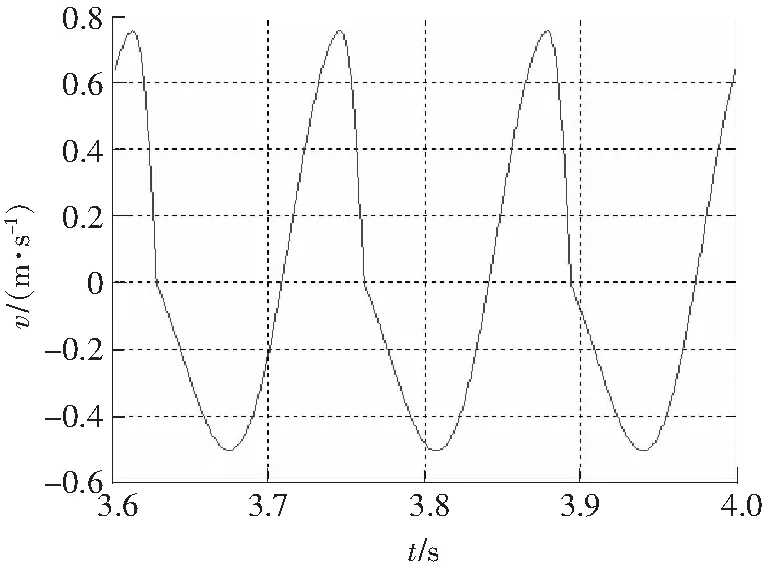
圖7 速度歷程Fig.7 Speed course

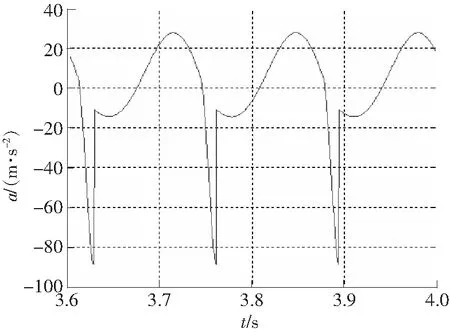
圖8 加速度歷程Fig.8 Acceleration course

由圖6—圖8可知：

1)位移歷程的正向幅值小于負向幅值，是非對稱的。圖6顯示當正向幅值是9.3 mm時，負向幅值是-15.5 mm。

2)速度歷程形狀與簡諧波發生了很大變化，也是非對稱的，正向峰值大于負向峰值，且速度在正向沖擊時達到峰值的時間較短，在負向返回時達到峰值的時間較長。

3)加速度歷程有一狹窄峰值，當沖擊發生時，加速度突然增大但時間很短。

4)由于位移、速度、加速度歷程與典型間歇運動曲線有很大不同，故質量塊的運動并不是簡單的簡諧運動，其非線性沖擊力是較大影響因素。

4 結 論

應用榮格庫塔(Runge-Kutta)4階法對單邊單質量沖擊振動破碎系統進行數值計算和分析得出以下結論：

1)非線性沖擊力是振動系統中影響較大的一個因素，且質量塊的運動并非簡單的簡諧運動。

2)幅頻曲線、沖擊力曲線和能量吸收曲線受間隙、激振頻率影響的規律，為振動破碎工藝的設計提供了參考——應盡可能讓物料與破碎頭之間的間隙值小，這樣就能用更小的激振力達到更好的破碎效果，且系統最好工作在主共振區以獲得大的沖擊力。

本文只針對大顆粒物料進行了研究，小顆粒物料振動系統的振動性態更為復雜，需進一步深入研究。

/

[1] 倪素環. 振動輥式破碎機破碎過程的非線性動力學分析[D].秦皇島：燕山大學，2006.

NI Suhuan.The Nonlinear Dynamics Analysis of the Crushing Process of the Vibrating Roller Crusher[D].Qinhuangdao: Yanshan University,2006.

[2] 倪素環,陳青果.顆粒層受壓破碎過程的試驗研究[J].金屬礦山，2011(1)：109-112.

NI Suhuan,CHEN Qingguo.Experimental studying on granular material compression crushing[J].Metal Mine,2011(1)：109-112.

[3] 朱海東.單質量雙邊沖擊振動破碎系統非線性動力學分析[J].甘肅科技，2011，27(2)：36-37.

ZHU Haidong.The nonlionar dynamics analysis on vibration-impact crushing system of a bilateral single-mass[J]. Gansu Science and Technology,2011,27(2):36-37.

[4] 趙月靜,彭偉,侯書軍,等.振動圓錐破碎機的動力學響應分析[J].河北科技大學學報,2006,27(3):230-233.

ZHAO Yuejing,PENG Wei,HOU Shujun,et al.Dynamics equations analysis of the vibration-cone-crusher[J].Journal of Hebei University of Science and Technology,2006,27(3):230-233.

[5] 熊洋,蔡改貧,夏劉洋,等.振動破碎機試驗與工作參數優化分析[J].有色金屬(選礦部分)，2015(5)：56-59.

XIONG Yang,CAI Gaipin,XIA Liuyang,et al.Vibration crusher test and work parameter optimization analysis[J].Nonferrous Metals(Mineral Processing Section),2015(5):56-59.

[6] 戴德成.非線性振動[M].南京：東南大學出版社,1992:7-14.

[7] 侯書軍.雙質體線性振動系統的動力學研究[J].河北科技大學學報,2003,24(2):1-4.

HOU Shujun.Dynamic research on linear vibration system of double mass[J].Journal of Heber University of Science and Technology， 2003，24(2):1-4.

[8] 王旭,劉方明,張以哲.基于慣性振動破碎技術實現物料細碎的研究[J].有色金屬(選礦部分)，2016(3)：66-71.

WANG Xu,LIU Fangming,ZHANG Yizhe.Research on materials fine crushing based on inertia vibrating crushing technology[J].Nonferrous Metals(Mineral Processing Section)，2016(3)：66-71.

[9] 劉樹英，韓清凱，聞邦椿.新型振動破碎機非線性動力學分析[J].振動與沖擊,2000，19(3)：34-36.

LIU Shuying,HAN Qingkai,WEN Bangchun. The nonlionar dynamics analysis of the new vibrating crusher[J]. Journal of Vibration and Shock，2000,19(3):34-36.

[10] 張軍翠，王立成，侯書軍.振動沖擊破碎系統的非線性動力學分析[J].礦山機械，2007(10)：51-54.

ZHANG Juncui,WANG Licheng,HOU Shujun.The nonlionar dynamics analysis on vibration-impact crushing system[J]. Mining machi-nery,2007(10)：51-54.

[11] 侯書軍,張躍軍,陳予恕.慣性振動破碎機的動力學分析[C]// 全國振動與波的利用學術會議.沈陽:東北大學出版社,2000:55-59.

[12] 劉劍飛,胡時勝,胡元育,等.花崗巖的動態壓縮實驗和力學性能研究[J].巖石力學與工程學報，2000,19(5):618-621.

LIU Jianfei,HU Shisheng,HU Yuanyu,et al.Dynamic compression experiment and mechanical properties of granite[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(5):618-621.

[13] 韓清凱,劉杰, 聞邦椿.不對稱滯回模型的一般形式及其參數慢變特性[J].振動與沖擊,2000,19(3):14-17.

HAN Qingkai,LIU Jie,WEN Bangchun.Asymmterical hysteretic model of general type and the parameters are slow to change[J].Journal of Vibration and Shock,2000,19(3):14-17.

[14] 韓清凱, 聞邦椿.一種不對稱滯回受迫振動系統及其分析[J].振動工程學報,1998,11(3):291-297.

HAN Qingkai,WEN Bangchun.An asymmetric hysteresis vibration system and its analysis[J].Journal of Vibration Engineering,1998,11(3):291-297.

[15] LACARBONARA W, VESTRONI F. Nonclassical responses of oscillators with hysteretic[J]. Nolinear Dynamics, 2003, 32:235-258.

[16] ABRAHAM I T, JEE A C. Approximate asymptotics for a nonlinear mathieu equation using harmonic balance based averaging[J]. Nonlinear Dynamics, 2003,31:347-365.

[17] DAS L, JEE A C. Multiple scales via galerkin projections:approximate asymptotics for strongly nonlinear oscillations[J]. Nonlinear Dynamics, 2003,32:161-186.

[18] ZHANG Aimin, LIU Qiaoling, WEN Bangchunn. Dynamic research of a nonlinear stochastic vibratory machine[J]. Shock and Vibration, 2002,9:277-281.

[19] BABITSKY V I. Theory of Vibro-Impact System and Application[M]. Berlin: Springer-Verlag, 1998:103-125.

[20] 聞邦春，劉鳳翅.振動機械的理論及應用[M].北京 :機械工業出版社，1980:240-253.

[21] 魏海燕,聞邦椿.慣性圓錐破碎機的非線性動力學特性研究[C]//全國振動與波的利用學術會議.沈陽:東北大學出版社，2000:60-63.

Nonlinear dynamic analysis of single-sided & single-mass crushing system under impact and vibration

NI Suhuan， YANG Xue

(School of Mechanical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018,China)

To research and develop efficient vibrating type crusher, a single-sided dynamic model is established for the impact and vibration crushing system, and the differential equation of vibration is set up with Newton's law for dynamic analysis. By making amplitude frequency curve, hysteretic impact force curve and energy absorption curve, the influence of which on the system response is analyzed. Based on the conclusion and using numerical method, the primary forced resonance of the system is calculated, and the time history of displacement, velocity and acceleration is obtained, showing that the motion mass movement is not a simple harmonic motion, the nonlinear impact force is one of the factors that influences the vibration system, and the influence rules of clearance, vibration frequency on the amplitude frequency curve, impact force and energy absorption are also obtained. The gap between the material and the broken head should be kept as small as possible so as to achieve a better crushing effect with a smaller excitation force, and the system is best to work in the main resonant area to get a big impact. The research result provides reference for further study of rules and mechanism of the vibration systems.

ore processing; single -sided & single- mass; amplitude frequency; impact force; energy absorption; dynamics

TH113.1

A

2017-07-01；

2017-08-25；責任編輯：馮 民

倪素環(1971—)，女，河北石家莊人，講師，碩士，主要從事機電專業方面的教學與研究。

E-mail:suhuan-ni@126.com

倪素環，楊 雪.沖擊振動單邊單質量破碎系統的非線性動力學分析[J].河北科技大學學報,2017,38(5):469-473.

NI Suhuan，YANG Xue.Nonlinear dynamic analysis of single-sided & single-mass crushing system under impact and vibration[J].Journal of Hebei University of Science and Technology,2017,38(5):469-473.