復合材料帶纏繞成型過程建模及工藝參數優化

俞 濤，史耀耀，鄧 博，何曉東，康 超，宋士博

(西北工業大學 機電學院，西安 710072)

2016-07-01；

2016-07-25。

國家自然科學基金(51375394)。

俞濤(1985—)，男，博士生，研究方向為復合材料成型工藝及裝備技術。E-mailscor00@163.com

復合材料帶纏繞成型過程建模及工藝參數優化

俞 濤，史耀耀，鄧 博，何曉東，康 超，宋士博

(西北工業大學 機電學院，西安 710072)

復合材料帶纏繞成型過程中，成型工藝參數的選取決定了纏繞制品的性能。采用正交實驗法研究各工藝參數對纏繞制品層間剪切強度的影響規律和敏感度，并將正交試驗數據與神經網絡理論相結合，對帶纏繞成型過程進行建模，得到纏繞成型工藝參數與層間剪切強度之間的非線性映射關系，并通過實驗驗證了模型的可靠性。在此基礎上，利用粒子群優化方法在可行工藝參數域內對纏繞成型工藝參數進行優化。仿真與實驗結果表明，基于神經網絡模型的工藝參數粒子群優化算法能夠快速、準確的得到帶纏繞成型的全局最優工藝參數組合。使得纏繞制品層間剪切強度達到最優的工藝參數組合為：加熱溫度115 ℃，纏繞張力357 N，壓輥壓力1006 N和纏繞速度0.28 m/s，在最優工藝參數作用下，纏繞制品的層間剪切強度達到102.2 MPa。

復合材料帶纏繞工藝；層間剪切強度；粒子群優化算法；BP神經網絡模型；參數優化

0 引言

復合材料預浸膠帶纏繞制品具有比強度高、高溫性能好和質量輕等諸多優點，已被廣泛應用于航空航天發動機的殼體、尾噴管和鼻錐等零部件中[1-2]。隨著復合材料纏繞成型部件用量的增加，人們對其性能的關注度也逐漸提高。在實際生產中，影響纏繞制品性能的因素較多，而纏繞成型工藝方法和成型工藝過程中工藝參數的選取對制品性能的影響較大[3]。因此，控制復合材料帶纏繞成型工藝過程、優化成型工藝過程中的工藝參數是控制制品質量的關鍵。

目前，關于復合材料成型過程中工藝參數對制品質量的影響已得到廣泛的關注。其中，基于成型過程數學建模及仿真方法的工藝參數研究已比較充分。如Schledjewski等學者開發了一種纖維增強復合材料仿真工具[4]，并對預浸膠帶鋪放過程進行分析，利用該仿真工具對鋪放速度、溫度和結合壓力等關鍵工藝參數對鋪放制品質量的影響進行研究[5-6]。但在工藝建模過程中，為便于計算和處理，不可避免的需要對模型進行一些近似和假設，最終會導致仿真結果出現難以控制的偏差。因此，基于實驗方法的工藝參數優化同樣被大量的應用在復合材料成型工藝中。如西安交通大學的段玉崗等采用正交實驗法對復合材料鋪放過程中的壓緊力、加熱溫度和芯模溫度對制品力學性能的影響進行了研究[7]。Tauseef和Bijan利用響應面法對纖維鋪放過程工藝參數進行了分析和優化[8]。正交實驗法能夠在離散的點中尋找到具有最優值的點，而并不能保證該點為連續空間內的最優點[9]。響應面法雖然能找到整個區域內的最佳優化點，但其二次多項式回歸模型過于單一，并不一定能準確的描述工藝參數與制品質量之間的非線性關系。

神經網絡具有高度的非線性函數逼近能力、自適應學習能力和容錯能力等優點，為解決不確定非線性系統的建模提供了新的方法[10]。本文在利用正交實驗法分析帶纏繞成型工藝參數對制品質量影響規律的基礎上，將神經網絡理論與正交試驗數據相結合，建立纏繞成型工藝參數與層間剪切強度的非線性映射關系。在驗證模型可靠性的前提下，采用粒子群優化(PSO)方法在可行工藝參數域內對纏繞成型工藝參數進行優化，為復合材料成型工藝的建模與優化研究提供了一種新的思路。

1 層間剪切強度正交實驗及分析

復合材料帶纏繞成型過程的實現是通過特定的機械運動和控制，將已經浸過樹脂膠液的布帶(如玻璃纖維布、碳纖維布等)，按照所要求的線型規律纏繞上芯模表面。在纏繞過程中，預浸膠帶被裝載在纏繞小車的料盤上，在膠帶通過磁粉離合器和熱壓輥后，與已纏繞在芯模上的層合板相互結合。預浸膠帶由于受溫度的影響使得樹脂基體的粘度降低，在壓力的共同作用下與基層層合板緊密接觸。同時，加熱和加壓也會使得層與層之間結合的界面處變得光滑，從而減少層間孔隙含量。帶纏繞成型工藝如圖1所示。

根據帶纏繞成型工藝過程的分析可知，當預浸膠帶在纏繞小車的運動下按預定軌跡纏繞在芯模上后，膠帶層與層之間的結合強度決定了纏繞完成的復合材料制品質量。對于復合材料纏繞制品來說，層間剪切強度是考查其層合板間結合強度的量化指標，也是檢驗其質量好壞的重要標準之一[11]。結合實際生產經驗可知，影響纏繞制品層間剪切強度的因素主要有纏繞速度、壓輥壓力、加熱溫度和纏繞張力。為研究上述工藝參數對層間剪切強度的影響規律和影響程度，采用四因素三水平正交實驗，并對實驗結果進行分析。

實驗所采用的預浸膠帶材料為中復神鷹碳纖維股份有限公司生產的碳纖維/環氧樹脂預浸膠帶，樹脂基體為YH-69環氧樹脂，纖維增強體為T-300碳纖維，膠帶寬度80 mm，單層平均厚度0.2 mm，膠帶采用二維編織，編織方向為0°/90°，碳纖維質量分數為62%。纏繞成型設備為KUKA纏繞機器人，纏繞成型過程如圖2所示。固化設備為山東眾泰達工業裝備有限公司公司生產的1200×3000型熱壓罐，層間剪切強度檢測設備采用長春試驗機研究所生產的CSS-88010電子萬能試驗機。四因素三水平纏繞成型正交實驗的規劃如表1所示。

根據正交實驗的規劃，使用纏繞機在不同纏繞速度、溫度、壓力和張力下進行平疊纏繞，所用芯模為直徑150 mm的圓柱芯模, 纏繞試件直徑160 mm。將纏繞完成的試件進行固化和脫模，固化時升溫速率為2.5 ℃/min，當溫度從室溫升至125 ℃時保持150 min，固化壓力為0.15 MPa。根據國標GB/T 1458—2008“纖維纏繞增強塑料環形試樣力學性能試驗方法”的規定[12]，將脫模下來的纏繞試件進行機加，得到標準的NOL(Naval Ordnance Laboratory)環，用于層間剪切強度實驗的NOL環內徑為(150±0.2)mm，寬度為(6±0.2)mm，厚(3±0.1)mm。再由每個NOL環徑向切取3個弧形剪切試樣，試樣獲取過程如圖3所示。

表1 正交實驗表L9(3)4

對從NOL環上切取的弧形試樣進行三點彎曲試驗便可測定纏繞試件的層間剪切強度，實驗過程如圖4所示。

圖4中，實驗夾具是為試樣進行三點彎曲試驗而專門制造的，其滑動支座允許試件自由伸長且支撐位置不變，從而消除試件由于變形與支座產生的摩擦力對測試結果的不利影響。試驗開始后，加載桿均勻、連續地對試樣施加載荷，加載速度為1 mm/min，直至試樣發生層間剪切破壞，并記錄破壞載荷。 將破壞載荷帶入式(1)便可計算出該試樣的層間剪切強度。

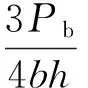
(1)

式中τs為層間剪切強度；Pb為破壞載荷；b為試樣寬度；h為試樣厚度。

將實驗所得數據錄入正交實驗表便可對各工藝參數對層間剪切強度的影響規律和敏感度進行分析。

在表1中，Km為某個因素第m水平所對應實驗指標(層間剪切強度)的平均值。根據Km的數值可以直觀的反應各工藝參數對層間剪切強度的影響規律，如圖5所示。

表1中R為極差，是各因素不同水平下實驗結果均值的最大值與最小值之差，如式(2)所示:

Rj=max(Kj1,Kj2,…,Kjm)-min(Kj1,Kj2,…,Kjm)

(2)

該指標反映了某列因素水平變動時實驗指標的變動幅度[13]。若R越大，則說明該工藝參數對層間剪切強度的影響越大。反之，則越小。依據R的大小可判斷各工藝參數的敏感程度。根據實驗結果(圖6)可看出，在帶纏繞成型工藝中，各工藝參數的敏感度從大到小依次為：加熱溫度、壓輥壓力、纏繞速度和纏繞張力。

2 帶纏繞成型工藝神經網絡建模

2.1 神經網絡建模

誤差反向傳播神經網絡(BP神經網絡)是一種前饋階層網絡的學習算法，在理論上，具有三層網絡的BP神經網絡模型(具有偏差和至少一個S型隱含層加上一個線性輸出層的網絡)能以足夠精度逼近任意非線性系統[14]。復合材料帶纏繞成型過程為典型的多輸入非線性過程，其中輸入層的主要工藝參數為：加熱溫度、壓輥壓力、纏繞速度和纏繞張力，輸出層為層間剪切強度。帶纏繞成型過程BP神經網絡模型結構如圖7所示。

該神經網絡模型采用三層網絡結構：輸入層4個節點，隱含層6個節點，輸出層1個節點。依據神經網絡模型的計算原則，隱含層和輸出層的輸出分別為

(3)

(4)

式中xi為輸入層第i個節點的輸入；yj為隱含層第j個節點的輸出；zk為輸出層第k個節點的輸出；wij為輸入層第i個節點到隱含層第j個節點之間的權值；θj為隱含層第j個節點的閥值；vjk為隱含層第j個節點到輸出層第k個節點之間的權值；ηk為輸出層第k個節點的閥值；f(x)、g(x)分別為輸入層與隱含層、隱含層與輸出層之間的傳遞函數。

這里，輸入層與隱含層之間使用Sigmoid傳遞函數，如式(5)所示。隱含層與輸出層之間使用線性Purelin函數，如式(6)所示：

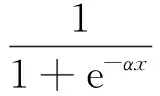
(5)

g(x)=αx+b

(6)

式中a、b和α為系數，在此均取1。

結合式(3)和式(4)，該纏繞成型過程BP神經網絡模型為

(7)

網絡訓練方法采用共軛梯度算法，該算法具有計算簡單、收斂速度快等優點，適用于中小型網絡[15]。由于神經網絡模型的預測精度與訓練樣本數據的多少有直接關系，除了將正交實驗的9組數據作為訓練樣本外，還應按照上述實驗方法以不同的工藝參數組合進行多組實驗，并將實驗結果用做神經網絡的訓練樣本以提高預測模型的準確性。

2.2 模型訓練及驗證

將實驗所得的30組數據分為2組，其中25組數據與正交實驗的9組數據共同組成神經網絡的訓練樣本，另外5組數據作為測試樣本以驗證該模型的預測精度。根據訓練樣本對所建立的神經網絡模型進行訓練，當網絡訓練達到期望的誤差精度時停止訓練，神經網絡模型訓練完成。圖8為訓練過程中的誤差曲線，該網絡在訓練到20次左右時開始收斂，在訓練237次后滿足目標誤差。

圖9為樣本值與網絡輸出值之間的對比圖。從圖9可看出，樣本值與網絡輸出值已非常接近，但為了驗證該神經網絡的預測精度和泛化性，采用5組訓練樣本以外的測試樣本對訓練好的網絡進行檢驗。實驗值與仿真值對比結果如表2所示。通過對比可知，模型預測值與實驗值之間的相對誤差不超過8%，說明該神經網絡模型能夠較好的反映各工藝參數與層間剪切強度之間的非線性映射關系。

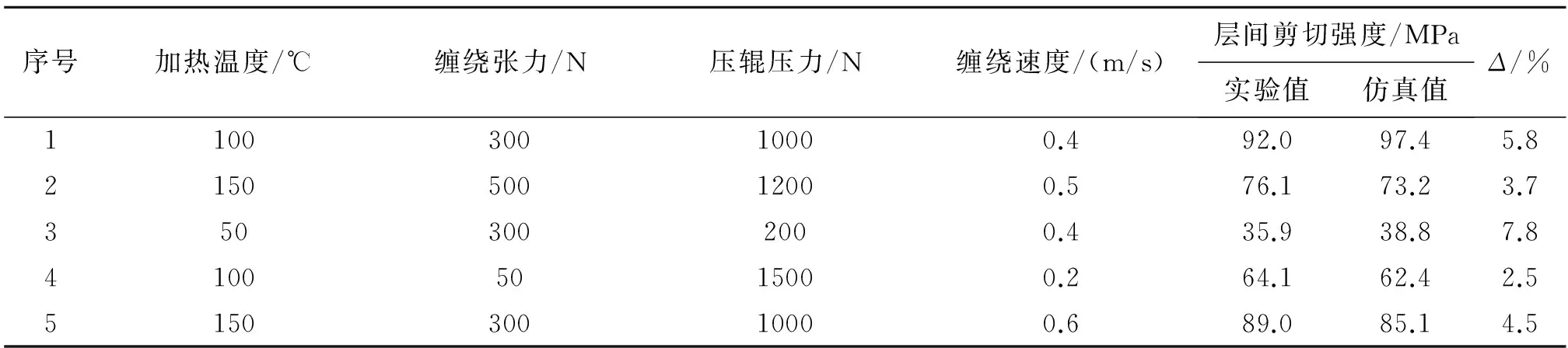
序號加熱溫度/℃纏繞張力/N壓輥壓力/N纏繞速度/(m/s)層間剪切強度/MPa實驗值仿真值Δ/%110030010000.492.097.45.8215050012000.576.173.23.73503002000.435.938.87.841005015000.264.162.42.5515030010000.689.085.14.5

3 基于粒子群算法的工藝參數優化

粒子群優化(PSO)算法以其精度高、收斂快、算法簡單且易于實現等優點被廣泛的用于解決實際工程優化問題[16-17]。根據PSO算法原理結合帶纏繞成型過程，將每一組工藝參數組合看成一個粒子，那么每個粒子所對應的適應值則為層間剪切強度，利用神經網絡模型作為適應度函數，便可在合理工藝參數范圍(解空間)內對參數進行優化。在優化過程中，首先在可行工藝參數范圍內隨機初始化一群工藝參數組合，每個工藝參數組合根據特定的函數來更新自己的速度和參數值，工藝參數組合追隨每次迭代中的最優參數組合在工藝參數范圍內進行搜索，直至達到最大迭代次數或找到滿意解為止。基于神經網絡模型的帶纏繞成型工藝參數PSO算法優化步驟如下：

(1)根據理論或經驗確定待優化工藝參數的范圍，在不同工藝參數組合下進行實驗，收集實驗數據。

(2)利用實驗數據建立工藝參數與層間剪切強度之間的BP神經網絡模型，并對該模型的可靠性進行驗證。

(3)PSO算法的初始化設定，如學習因子、慣性權重、種群規模和最大迭代次數等，并隨機初始化粒子群的位置和速度。

(4)將粒子群代入所建立的神經網絡中計算每個粒子的適應值，確定粒子個體極值和種群最優值。

(5)根據特定的函數來更新粒子群的速度和位置。速度更新、位置更新如式(8)、式(9)所示。

(8)

(9)

(6)判斷種群最優適應值是否滿足精度要求或是否達到最大迭代次數。若滿足條件則停止計算，輸出全局最優值，否則返回步驟(4)重新計算。該優化算法的流程圖如圖10所示。

根據實際生產經驗，帶纏繞成型待優化工藝參數的范圍設定為：溫度50～150 ℃，壓力100～1500 N，張力50～500 N，速度0.2～0.6 m/s[18]。在該工藝參數范圍內，按照上述優化算法思想對帶纏繞成型過程進行建模、仿真和優化計算便可得到最優層間剪切強度值及其對應的工藝參數組合。為驗證優化效果，使用優化得到的工藝參數組合進行纏繞和三點彎曲實驗，并將實驗結果與仿真結果進行對比，如表3所示。結果表明，使得帶纏繞成型制品層間剪切強度達到最優的工藝參數組合為：加熱溫度115 ℃，纏繞張力357 N，壓輥壓力1006 N，纏繞速度0.28 m/s。此時，纏繞制品的層間剪切強度達到102.2 MPa。

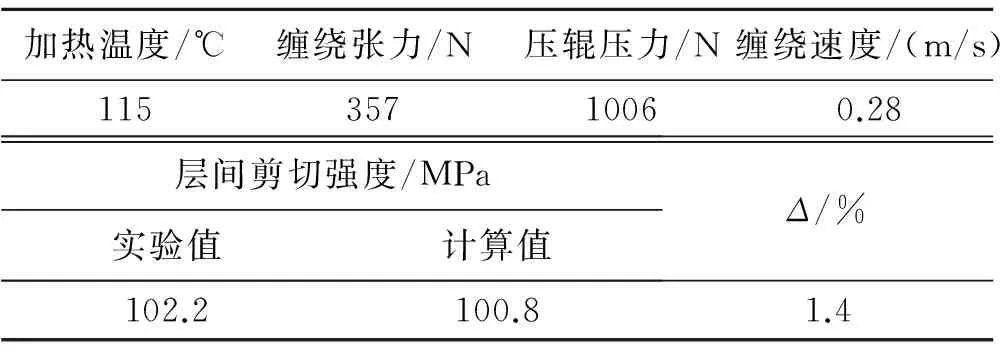
表3 參數優化結果

雖然該模型可較好地反映各工藝參數和層間剪切強度之間的非線性映射關系，但通過模型驗證和優化結果中仿真值與實驗值的對比可知，該模型仍然存在一定的誤差，產生誤差的原因主要包括以下兩方面：一是實驗過程中的不確定性因素導致的實驗數據失真；二是訓練數據偏少導致的網絡擬合精度不夠。因此，在實際優化過程中，可通過如下方法來進一步提高模型的預測精度：

(1)增加每組工藝參數組合的實驗次數，利用取平均值的方法減少失真數據帶來的影響。

(2)增加BP神經網絡的訓練樣本數據，提高網絡的擬合精度。

4 結論

(1) 根據正交試驗和極差分析可知，帶纏繞成型工藝中的關鍵工藝參數對纏繞制品的層間剪切強度均有不同程度的影響，且敏感度從大到小依次為：加熱溫度、壓輥壓力、纏繞速度和纏繞張力。

(2)帶纏繞成型過程BP神經網絡模型能夠準確的描述各工藝參數與層間剪切強度之間的非線性映射關系，該模型仿真誤差小于8%。

(3) 基于神經網絡模型的工藝參數PSO算法能夠快速、準確的得到帶纏繞成型的全局最優工藝參數組合。仿真和實驗結果表明，當纏繞溫度為115 ℃，壓力為1006 N，張力為357 N，速度為0.28 m/s時，層間剪切強度達到102.2 MPa，纏繞制品的結合強度最優。

[1] Dirk H J A L,Ward C,Potter K D. The engineering aspects of automated prepreg layup: History,present and future[J]. Composites Part B: Engineering,2012,43(3): 997-1009.

[2] Dai S C,Ye L. Characteristics of CF/PEI tape winding process with on-line consolidation[J]. Composites Part A: Applied Science and Manufacturing,2002,33(9): 1227-1238.

[3] 唐邦銘. 熱塑性預浸帶纏繞工藝參數及加熱方式對成型質量及內應力的影響[J]. 復合材料學報,1999,16(2): 22-29.

[4] Schledjewski R,Latrille M. Processing of unidirectional fiber reinforced tapes-fundamentals on the way to a process simulation tool (ProSimFRT)[J]. Composites Science and Technology,2003,63(14): 2111-2118.

[5] Khan M A,Mitschang P,Schledjewski R. Identification of some optimal parameters to achieve higher laminate quality through tape placement process[J]. Advances in Polymer Technology,2010,29(2): 98-111.

[6] Khan M A,Mitschang P,Schledjewski R. Parametric study on processing parameters and resulting part quality through thermoplastic tape placement process[J]. Journal of Composite Materials,2013,47(4): 485-499.

[7] 段玉崗,劉芬芬,陳耀,等. 纖維鋪放壓緊力及預浸帶加熱溫度對復合材料力學性能的影響[J]. 復合材料學報,2012,19 (4): 148-156.

[8] Aized T,Shirinzadeh B. Robotic fiber placement process analysis and optimization using response surface method[J]. The International Journal of Advanced Manufacturing Technology,2011,55(1-4): 393-404.

[9] 田榮鑫,姚倡鋒,黃新春,等. 面向加工表面粗糙度的鈦合金高速銑削工藝參數區間敏感性及優選[J]. 航空學報,2010,31(12): 2464-2470.

[10] 倪立斌,劉繼常,伍耀庭,等. 基于神經網絡和粒子群算法的激光熔覆工藝優化[J]. 中國激光,2011,38(2): 99-104.

[11] 李旭武,周曉東,郭兵兵,等. 工藝條件對兩步法纏繞成型連續玻璃纖維增強聚丙烯管材層間剪切強度及樹脂含量的影響[J]. 玻璃鋼/復合材料,2011(6): 64-67.

[12] GB/T 1458-2008 纖維纏繞增強塑料環形試樣力學性能試驗方法[S]. 中華人民共和國國家標準,2008.

[13] Cui W,Li X,Zhou S,et al. Investigation on process parameters of electrospinning system through orthogonal experimental design[J]. Journal of Applied Polymer Science,2007,103(5): 3105-3112.

[14] 夏克文,李昌彪,沈鈞毅. 前向神經網絡隱含層節點數的一種優化算法[J]. 計算機科學,2005,32(10): 143-145.

[15] 陳曉平. 薄殼件注塑成型工藝參數優化研究[D]. 浙江大學,2005.

[16] Parwar P J,Rao R V,Davim J P. Multiobjective optimization of grinding process parameters using particle swarm optimization algorithm[J]. Materials and Manufacturing Processes,2010,25(6): 424-431.

[17] Yang B. Process parameters optimization of plasma spraying nanostructured coating based on particle swarm optimization algorithm[J]. Applied Mechanics and Materials,2014(665):68-71.

[18] 史耀耀,俞濤,何曉東,等. 復合材料帶纏繞成型工藝參數耦合機制及優化[J]. 復合材料學報,2015,21(3): 831-839.

Modelingandparametersoptimizationofcompositetapewindingprocess

YU Tao, SHI Yao-yao, DENG Bo, HE Xiao-dong, KANG Chao, SONG Shi-bo

(Department of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China)

In the winding process of the composite tapes, parameters selection in the molding step plays a profoundly important role to determine the quality of winding product. In this paper, the mechanism and effect of process sensitivity parameters on interlaminar shear strength for tape winding product is investigated based on orthogonal experimental method. The tape winding process model is established by combining the orthogonal experimental data with the neural network theory. The nonlinear map relationship of winding process parameters and interlaminar shear strength is obtained, and the reliability of process model is verified according to experimental test. The winding process parameters are optimized within the feasible region using particle swarm optimization algorithm. The experimental and simulation results show that the global optimal parameters combination for tape winding process can be obtained quickly and accurately by the particle swarm optimization algorithm based on the BP neural network model. The optimal setting of the process parameters for interlaminar shear strength is: temperature of 115 ℃, tension of 357 N, pressure of 1006 N and velocity of 0.28 m/s. Under the effect of the optimal processing parameters, the interlaminar shear strength of the winding products can reach 102.2 MPa.

composite tape winding process；interlaminar shear strength；particle swarm optimization；BP neural network model；parameters optimization

V258

A

1006-2793(2017)05-0627-07

10.7673/j.issn.1006-2793.2017.05.017

(編輯：呂耀輝)