關于三次Diophantine方程x3+1=2p1p2Qy2的可解性

楊海，候靜，付瑞琴

(1. 西安工程大學理學院，陜西 西安 710048；2. 西安石油大學理學院，陜西 西安 710065)

關于三次Diophantine方程x3+1=2p1p2Qy2的可解性

楊海1，候靜1，付瑞琴2

(1. 西安工程大學理學院，陜西 西安 710048；2. 西安石油大學理學院，陜西 西安 710065)

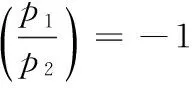
三次Diophantine方程；正整數解；同余條件

Diophantine方程是數論中一個古老而又十分重要的分支，因為其研究內容之豐富、未解決問題與猜想之多、入門之容易和解決之困難而著名。尋求Diophantine方程的整數解是數論研究中的一項重要內容。近幾十年來，Diophantine方程理論不僅自身的發展異常活躍，而且全面應用于數學相關的其他各個領域。如邵檬[1]制定了丟番圖四定理，解決了數論中任意正整數究竟能分解成幾個平方數之和的這一古老問題。王澤輝[2]基于數論中大數分解的困難性設計了新算法并對RSA 密碼制的解密進行了研究。三次Diophantine方程的求解是一個十分困難的問題，但是其研究方法與理論成果在代數數域(二次域類數)、組合設計、圖論、有限單群甚至編碼和密碼學等領域均有重要的應用。令N是全體正整數的集合。對于無平方因子正整數D, 方程

x3+1=Dy2,x,y∈N

(1)

是一類討論較多的三次Diophantine方程(參見文獻[3-7])。本文研究了上述三次Diophantine方程的可解性，給出了該方程無解的同余條件。

1 定理及推論

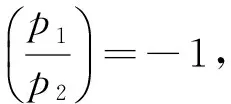
D=2p1p2Q

(2)

時無解的充分條件。最近，杜先存等[6]證明了：當D=2p1p2Q時，如果p1,p2,Q滿足

p1≡1(mod 8),

p2≡5(mod 8),

Q≡5,13(mod 24)

(3)

或

p1≡5(mod 8),

p2≡3(mod 8),

Q≡3(mod 4)

(4)

那么方程(1)無解(x,y)。本文應用初等數論方法進一步證明了以下結果：

定理1 當D滿足式(2)時，如果p1,p2,Q滿足

p1≡1(mod 8),

p2≡5(mod 8),

Q≡1(mod 4)

(5)

那么方程(1)無解(x,y)。

顯然，上述定理改進了文獻[6]給出的條件(3)。同時，將文獻[6]的結果與本定理結合直接可得以下的：

推論1 當D滿足式(2)時，如果p1,p2,Q滿足式(4)或式(5)，那么方程(1)無解(x,y)。

2 定理的證明

首先引入有關Pell方程解的若干基本性質。對于非負整數n, 設

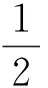
(6)

其中

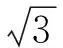
(7)

根據文獻[8-12]直接可得以下引理：

引理1 設m是非負整數。

(i)(u,v)=(un,vn)(n=1,2,…)是方程

u2-3v2=1,u,v∈N

(8)

的全部解。

(ii)

(iii)gcd(un,vn)=1,gcd(u2m+1,um+1vm+1)=2。

(iv)un的奇素因數q都滿足q≡1(mod 6)。

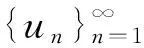
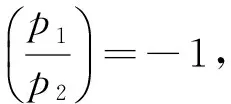
p1p2≡5(mod 8),

(9)

又因為Q的素因數q都滿足q≡5(mod 6), 所以由引理1的結論(ii)和(iv)可知

gcd(Q,un)=1

(10)

當D=2p1p2Q時，方程(1)可表為

x3+1=2p1p2Qy2,x,y∈N

(11)

設(x,y)是方程(11)的一組解。下面按照文獻[6]的分析可知，本定理的證明只需排除以下8種情形。

情形Ⅰ

x+1=2p1p2Qa2,x2-x+1=b2,

y=ab,a,b∈N

(12)

由式(12)得3=(2b)2-(2x-1)2≥2b+(2x-1)>3這一矛盾，故不可能。

情形Ⅱ

x+1=2p1Qa2,x2-x+1=p2b2,

y=ab,a,b∈N

(13)

由式(13)中第一個等式可知x≡-1(modp1), 將其代入式(13)中第二個等式可得p2b2≡3(modp1), 故有

(14)

情形Ⅲ

x+1=2p2Qa2,x2-x+1=p1b2,

y=ab,a,b∈N

(15)

此時，由公式(15)的第一個等式可知：x≡-1(modp2),p1b2≡3(modp2)以及

(16)

情形Ⅳ

x+1=2Qa2,x2-x+1=p1p2b2,

y=ab,a,b∈N

(17)

因為Q≡1(mod 4), 所以由式(17)中第一個關系式可得

(18)

又因為2不整除a, 所以由式(17)中第二個等式和式(18)可知

p1p2≡p1p2b2≡x2-x+1≡

(19)

情形Ⅴ

x+1=6p1p2Qa2,x2-x+1=3b2,

y=3ab,a,b∈N

(20)

在式(20)中消去x可得

(2b)2-3(4p1p2Qa2-1)2=1

(21)

由式(21)可知方程(8)有解(u,v)=(2b,4p1p2Qa2-1)適合v≡3(mod 4)。因此，根據引理1的結論(i)和(ii)可知2|a,

a=2c, 2b=u4r+3,

16p1p2Qc2-1=v4r+3,c,r∈N

(22)

因為由式(6)和式(7)可知

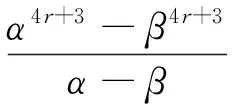
4u2r+1ur+1vr+1

(23)

所以由式(22)中第三個等式和式(23)可得

4p1p2Qc2=u2r+1ur+1vr+1

(24)

再由引理1的結論(iii)可知gcd(u2r+1,ur+1vr+1)=2, 從而根據式(10), 由式(24)僅可能推出以下3種情況：

u2r+1=2f2,ur+1vr+1=2p1p2Qg2

(25)

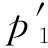
(26)

u2r+1=2p1p2f2,ur+1vr+1=2Qg2

(27)

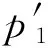
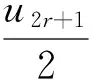
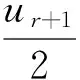
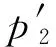
g=hk, 2不整除hk,h,k∈N

(28)

又因為Q≡1(mod 4)且k2≡1(mod 8), 所以根據引理1的結論(ii), 由式(28)中第二個式子可知r+1≡1(mod 4), 于是可得r=4s, 其中s是正整數。進而由式(26)和式(28)中第一個等式可得

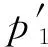
(29)

因為由引理1的結論(ii)可知u8s+1≡u4s+1≡2(mod 16), 又因為f2≡h2≡1(mod 8), 所以由式(29)可得

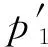
(30)

如果式(26)在2不整除r時成立，則因r=2t+1, 其中t是正整數，所以由式(26)中第二個等式可知

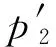
(31)

因為2不整除u2t+2,gcd(Q,u2t+2)=gcd(u2t+2,u2t+2)=1且u2t+2不是平方數，所以由式(31)可得

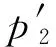
g=hk,h,k∈N

(32)

又因為gcd(Q,ut+1)=gcd(ut+1,vt+1)=1, 所以由式(32)中第二個等式可知

k1,k2∈N

(33)

但是，由引理1的結論(v)可知式(33)中第一個等式不成立。

如果式(27)成立，gcd(Q,ur+1)=gcd(ur+1,vr+1)=1, 所以由式(27)中第二個等式可知ur+1或ur+1/2必為平方數。然而，根據引理1的結論(v)可知這是不可能的。因此情形Ⅴ不成立。

情形Ⅵ

x+1=6p1Qa2,x2-x+1=3p2b2,

y=3ab,a,b∈N

(34)

由公式(34)可知

x≡-1(modp1), 3p2b2≡3(modp1),

p2b2≡1(modp1)

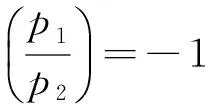
情形Ⅶ

x+1=6p2Qa2,x2-x+1=3p1b2,

y=3ab,a,b∈N

(35)

由式(35)可知

x≡-1(modp2), 3p1b2≡3(modp2),

p1b2≡1(modp2)

以及

與式(9)矛盾，故不可能。

情形Ⅷ

x+1=6Qa2,x2-x+1=3p1p2b2,

y=3ab,a,b∈N

(36)

因為Q≡1(mod 4), 所以由式(36)中第一個等式可知

(37)

又由式(36)中第二個等式和式(37)可得

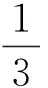
(38)

與式(9)矛盾，故不可能。

綜上所述即得本定理。證畢。

[1] 邵檬. 自然數八度周期律暨丟番圖四定理[J]. 中山大學學報(自然科學版), 2004, 43(4): 23-27.

SHAO M. The octet periodic law of natural numbers and the four theorems of Diophantus [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2004, 43(4): 23-27.

[2] 王澤輝. 大整數因子分解新算法及對RSA 密碼制的解密[J]. 中山大學學報(自然科學版), 2003, 42(5): 15-18.

WANG Z H. A novel calculation method for the factorization of large integral numbers and the decoding of the RSA cryptosystem [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2003, 42(5): 15-18.

[3] 柯召, 孫琦. 關于丟番圖方程x3±1=Dy2[J]. 四川大學學報(自然科學版), 1981, 18(2): 1-5.

KE Z, SUN Q. On the Diophantine equationx3±1=Dy2[J]. Journal of Sichuan University (Natural Science Edition), 1981, 18(2): 1-5．

[4] 柯召, 孫琦. 關于丟番圖方程x3±1=Dy2[J]. 中國科學, 1981, 24(12): 1453-1457.

KE Z, SUN Q. On the Diophantine equationx3±1=Dy2[J]. Scientia Sinica Mathematica, 1981, 24(12): 1453-1457．

[5] 杜先存, 萬飛, 楊慧章. 關于丟番圖方程x3±1=1267y2的整數解[J]. 數學的實踐與認識, 2013, 43(15): 288-292.

DU X C, WAN F, YANG H Z. On the Diophantine equationx3±1=1267y2[J].Mathematics in Practice and Theory, 2013, 43(15): 288-292．

[6] 杜先存, 管訓貴, 楊慧章. 關于不定方程x3±1=73qy2的整數解[J]. 西南師范大學學報(自然科學版), 2014, 39(6): 18-20.

DU X C, GUAN X G, YANG H Z. Integer solution of the indefinite equationx3±1=73qy2[J]. Journal of Southwest China Normal University (Natural Science Edition), 2014, 39(6): 18-20．

[7] 管訓貴, 杜先存. 關于Diophantine方程x3±1=pqy2[J].安徽大學學報(自然科學版), 2014, 38(1): 29-35.

GUAN X G, DU X C. On the Diophantine equationx3±1=pqy2[J]. Journal of Anhui University (Natural Science Edition), 2014, 38(1): 29-35．

[8] 杜先存. 關于不定方程x3±1=2PDy2的整數解[J]. 浙江大學學報(理學版), 2015, 42(3): 268-270, 275.

DU X C. Integer solution of the indefinite equationx3±1=2PDy2[J]. Journal of Zhejiang University (Science Edition), 2015, 42(3): 268-270, 275.

[9] 柯召, 孫琦. 談談不定方程[M]. 上海: 上海教育出版社, 2011.

[10] 曹珍富. 丟番圖方程引論[M]. 哈爾濱: 哈爾濱工業大學出版社, 2012.

[11] 曹珍富. 不定方程及其應用[M]. 上海: 上海交通大學出版社, 2000.

[12] 華羅庚. 數論導引[M]. 北京: 科學出版社, 1979.

OnthesolvabilityofthecubicDiophantineequationx3+1=2p1p2Qy2

YANGHai1,HOUJing1,FURuiqin2

(1. School of Science, Xi’an Polytechnic University, Xi’an 710048, China;2. School of Science, Xi’an Shiyou University, Xi’an 710065, China)

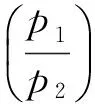
cubic Diophantine equation; positive integer solution; congruence condition

O156.7

A

0529-6579(2017)05-0030-04

10.13471/j.cnki.acta.snus.2017.05.004

2016-12-16

國家自然科學基金(11226038, 11371012)；陜西省自然科學基金(2017JM1025)；陜西省教育廳科研計劃項目(17JK0323)；西安石油大學博士科研項目 (2015BS06)

楊海(1979年生)， 男；研究方向數論及其應用；E-mail:xpuyhai@163.com