一類擴散食物鏈模型正解的多重性和唯一性
李海俠
(寶雞文理學院數學與信息科學學院,陜西 寶雞 721013)
一類擴散食物鏈模型正解的多重性和唯一性
李海俠
(寶雞文理學院數學與信息科學學院,陜西 寶雞 721013)
研究了一類具有Crowley-Martin反應函數的食物鏈模型。首先利用全局分歧理論和度理論討論了正解的存在性和多重性,得到了正解分歧的基本形狀。接著運用擾動理論給出了正解的唯一性和穩定性條件,結果表明當d充分大時系統在一定條件下存在唯一且穩定的正解。
Crowley-Martin反應函數;分歧;擾動;多重性;唯一性
本文在齊次Robin 邊界條件下討論如下具有C-M反應函數的食物鏈模型
其中 Ω∈RN是帶有光滑邊界?Ω的有界區域。系統(1)是食物鏈模型,其中u是食餌,v是以u為食物的捕食者,w是以v為食物的捕食者。r1和r3是食餌u和捕食者w的增長率。r2是捕食者v的死亡率。a1,a2,c和d分別代表了捕食者v的捕獲率、轉化率、處理時間和捕食者間的干擾度。u0(x),
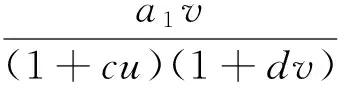
(1)
當系統(1)沒有捕食者w且d=0時,系統(1)變為具有Holling-II反應函數的兩物種捕食-食餌模型。文獻[12-14]在Neumann邊界條件下運用分歧理論研究了非常數正解的不存在性和存在性以及周期解的存在性。如果系統(1)沒有捕食者w,則系統(1)變為具有C-M反應函數的兩物種捕食-食餌模型。文獻[15]在Neumann邊界條件下考察了系統平衡態正解的圖靈不穩定性和Hopf分歧。
本文將重點考慮系統(1)對應的平衡態系統
(2)
正解的存在性、多重性、穩定性和唯一性。
令
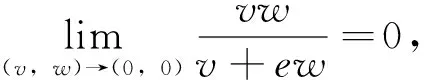
為了得到重要結論,這節最后給出一些預備知識。
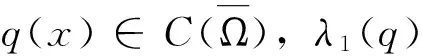
則λ1(q)連續依賴q,λ1(q)是簡單的。而且,如果q1≤q2,q1?q2,則λ1(q1)<λ1(q2)。為了簡單起見,記λ1(0)為λ1,相應于λ1的主特征函數記為 ?1,?1>0且‖?1‖∞=1。
考慮如下非線性問題
-Δu=u(r-u),x∈Ω;
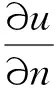
(3)
眾所周知,若r>λ1,則(3)有唯一正解。定義唯一正解為Θr。特別地,Θr≤r且Θr連續依賴r。
1 正解的存在性和多重性
本小節應用不動點指數理論和分歧理論討論系統(2)正解的存在性和多重性條件。首先類似文獻[17]定理2的證明給出系統(2)共存解的先驗估計。
引理1 如果a2r1>r2(1+r1c),則系統(2)的任意共存解(u,v,w)有先驗估計
u(x)≤r1,v(x)≤Q,w(x)≤r3+b2

注1 下面總假設a2>max{r2(1+r1c)/r1,cλ1}。
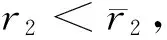
引理2 如果系統(2)有共存解,則r1>λ1,r2<Λ,r3+b2>λ1。
利用引理2和上下解方法易得

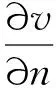
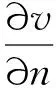
接下來,以r2為分歧參數研究系統(2)關于強半平凡解(Θr1,0,Θr3)的分歧。為了應用分歧理論引入如下空間:
令U=Θr1-u,V=v,W=w-Θr3,則U,V,W>0滿足
(4)
其中
G1(U,V,W)=U2+(Θr1-U)·
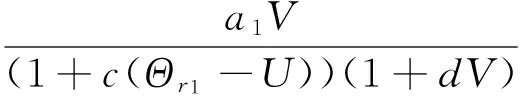
G2(U,V,W)=
G3(U,V,W)=
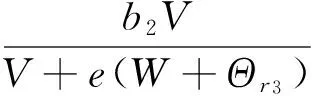
令
G(U,V,W)=
(G1(U,V,W),G2(U,V,W),G3(U,V,W))
顯然,G(0,0,0)=0且G連續。而且,Fréchet導數D(U,V,W)G(0,0,0)=0。令K是帶有Robin邊界條件的-Δ的逆,則問題(4)成為
定義T:R+×E→E為
T(r2,U,V,W)=
KG1(U,V,W),
則T(r2,U,V,W)是可微緊算子。令F=I-T。顯然,F是C1函數且F(r2,0,0,0)=0。而且,F(r2,U,V,W)=0當且僅當(r2,Θr1-U,V,Θr3+W)是系統(2)的非負解。
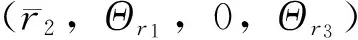
‖φ1‖2=1,
接著,將局部分歧延拓為全局分歧。
令r2,i(μ)(μ≥1)是如下特征值問題的特征值
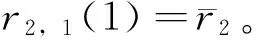





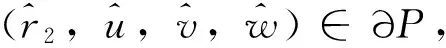
-ΔU=r1U,x∈Ω;

x∈Ω;
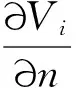

下面應用不動點指數理論討論系統(2)共存解的多重性。為此,記
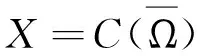
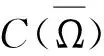

W=K⊕K⊕K,
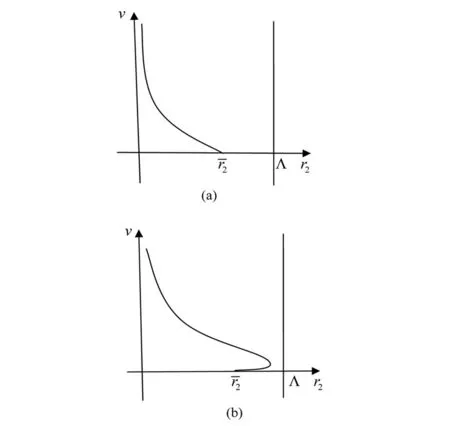
D={(u,v,w)∈W|u(x) v(x) 定義算子At:D→W為 At(u,v,w)=(-Δ+q)-1· 接下來運用類似文獻[19]的方法給出算子A在平凡解和半平凡解處的不動點指數,在此省略其證明。 引理4 (i) indexW(A,D)=1; (ii) 若r1≠λ1,r3>λ1,則indexW(A,(0,0,0))=0; (iii) 設r1>λ1。若r2<Λ,r3>λ1,則indexW(A,(Θr1,0,0))=0; (iv) 設r3>λ1。若r1>λ1,則indexW(A,(0,0,Θr3))=0; 下面計算A在P1的指數。結合引理4用類似于文獻[19]的方法有 引理5 若r1>λ1,r2<Λ,r3+b2>λ1, 則indexW(A,P1)=0。 由引理4、引理5和度的可加性得系統(2)正解的存在條件。 這里ν∈[0,1]。顯然系統(2)有非負解當且僅當A1在D中有不動點。 令D1=DDδ。由引理1可知Aν在?D1上沒有不動點。于是根據不動點指數的同倫不變性可知indexW(A1,D1)=indexW(A0,D1)。顯然A0在D1內有不動點(0,0,0),(Θr1,0,0),(0,0,Θr3)。用Dancer指數定理易證得在已知條件下A0在平凡解和半平凡解處的指數都為0。于是,indexW(A1,D1)=indexW(A0,D1)=1。最后結合引理4和引理5得 indexW(A1,D1)= indexW(A1,(0,0,0))+indexW(A1,(Θr1,0,0))+ indexW(A1,(0,0,Θr3))+indexW(A1,P1) 這表明系統(2)在DDδ內至少有一個正解。 圖1 系統(2)正解可能的分歧曲線(a) 定理2條件下;(b) 定理4條件下Fig.1 Possible bifurcation diagrams of positive solutions to system (2)(a) under the conditions of Theorem 2;(b) under the conditions of Theorem 4 這一節考察當d充分大時系統(2)正解的穩定性和唯一性。我們注意到當d充分大時,系統(2) 的正解只有一種類型。也就是說,如果(u,v,w)是系統(2)的任意正解,則對于充分大的d,(u,dv,w) 接近于如下問題的正解: (6) 如果r1>λ1,則問題(6)等價于 (7) 首先,我們給出系統(7)正解非退化和線性穩定的條件。 證明假設χ是系統(7)的正解,則由系統(7)可得 (8) 接下來,證明系統(7)任意正解的穩定性。假設χ是系統(7)的任意正解。考慮如下特征值問題 x∈Ω; (9) 由(9)得 于是唯一性得證。 又因為wi≥Θr3, 所以考慮如下兩種情況: (i) 如果v≡0。則(ui,vi,wi) 接近于(Θr1,0,Θr3),與假設矛盾; (ii)如果v≥0,?0,w>0。由Harnack不等式得v>0。于是h=0,v≡0。同情況(i)與假設矛盾。 這表明 ‖u-Θr1‖C1+‖v‖C1+‖w-Θr3‖C1≤σ 成立。 x∈Ω; (10) 設divi=χi。則χi滿足 (11) x∈Ω; (12) ; 最后給出系統(2)正解的穩定性和唯一性條件。 (13) (14) (15) 由式(15)的第一和第三個方程得ξ≡0,ζ≡0。如果η?0,則由式(15)的第二個方程可得 此矛盾表明系統(2)的任意共存解(如果存在) 是非退化和線性穩定的。 1=indexW(A,D)= 這表明系統(2)存在唯一正解。 本文在齊次Robin邊界條件下考察了一類擴散食物鏈模型共存解的存在性、多解性、穩定性和唯一性。研究結果表明當捕食者間的相互干擾度不強且物種v的死亡率在一定范圍內時,三物種出現多重共存態;當捕食者間的相互干擾度非常強且物種v的死亡率不超過某臨界值時,三物種出現唯一的穩定共存態。 [1] WANG M, WU Q. Positive solutions of a prey-predator model with predator saturation and competition [J]. J Math Anal Appl, 2008, 345(2): 708-718. [2] WEI M H, WU J H, GUO G H. The effect of predator competition on positive solutions for a predator-prey model with diffusion [J]. Nonlinear Analysis, 2012, 75(13): 5053-5068. [3] DONG Q L, MA W B, SUN M J. The asymptotic behavior of a Chemostat model with Crowley-Martin type functional response and time delays [J]. Journal of Mathematical Chemistry, 2013, 51(5): 1231-1248. [4] LIU X Q, ZHONG S M, TIAN B D, et al. Asymptotic properties of a stochastic predator-prey model with Crowley-Martin functional response [J]. Journal of Applied Mathematics and Computing, 2013, 43(1/2): 479-490. [5] 李海俠, 李艷玲. 一類帶有Crowley-Martin反應函數的捕食-食餌模型的定性分析[J]. 中山大學學報(自然科學版), 2014, 53(5): 66-72. LI H X, LI Y L. Qualitative analysis for a predator-prey system with Crowley-Martin functional response [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53(5): 66-72. [6] MENG X Y, HUO H F, XIANG H, et al. Stability in a predator-prey model with Crowley-Martin function and stage structure for prey [J]. Applied Mathematics and Computation, 2014, 232(3): 810-819. [7] LI H X. Asymptotic behavior and multiplicity for a diffusive Leslie-Gower predator-prey system with Crowley-Martin functional response [J]. Computers and Mathematics with Applications, 2014, 68: 693-705. [8] ZHOU J. Qualitative analysis of a modified Leslie-Gower predator-prey model with Crowley-Martin functional responses [J]. Communications on Pure and Applied Analysis, 2015, 14(3): 1127-1145. [9] LI S B, WU J H, DONG Y Y. Uniqueness and stability of a predator-prey model with C-M functional response [J]. Computers and Mathematics with Applications, 2015, 69(10): 1080-1095. [10] DONG Y Y, LI S B, LI Y L. Multiplicity and uniqueness of positive solutions for a predator-prey model with C-M functional response [J]. Acta Applicandae Mathematicae, 2015, 139(1): 187-206. [11] TRIPATHI J P, TYAGI S, ABBAS S. Global analysis of a delayed density dependent predator-prey model with Crowley-Martin functional response [J].Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1/2/3): 45-69. [12] WONLYUL K, KIMUN R. Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge [J]. J Differential Equations, 2006, 231(231): 534-550. [13] YI F Q, WEI J J, SHI J P. Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system [J]. J Differential Equations, 2009, 246(5): 1944-1977. [14] PENG R, SHI J P. Non-existence of non-constant positive steady states of two Holling type-II predator-prey systems: Strong interaction case [J]. J Differential Equations, 2009, 247(3): 866-886. [15] SAMBATH M, GNANAVEL S, BALACHANDRAN K. Stability and Hopf bifurcation of a diffusive predator-prey model with predator saturation and competition [J]. Applicable Analysis, 2013, 92(12): 2439-2456. [16] KUANG Y, BERETTA E. Global qualitative analysis of a ratio-dependent predator-prey system [J]. J Math Biol, 1998, 36(4): 389-406. [17] 姜洪領. 一類蜘蛛-昆蟲模平衡態正解的存在性[J]. 中山大學學報(自然科學版), 2016, 55(3): 64-67. JIANG H L. The existence of steady-state positive solutions for a spider-insect model [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(3): 64-67. [18] WU J H. Global bifurcation of coexistence state for the competition model in the chemostat [J].Nonlinear Analysis, 2000, 39(7): 817-835. [19] LI H X, LI Y L, YANG W B. Existence and asymptotic behavior of positive solutions for a one-prey and two-competing-predators system with diffusion [J]. Nonlinear Analysis: Real World Applications, 2016, 27: 261-282. Multiplicityanduniquenessofpositivesolutionstoadiffusivefood-chainmodel LIHaixia (Institute of Mathematics and Information Sciences, Baoji University of Arts and Sciences, Baoji 721013, China) A food-chain system with Crowley-Martin functional response is studied. By making use of the global bifurcation theory and degree theory, the existence and multiplicity of positive solutions are discussed and the basic shape of bifurcation curve of positive solutions is obtained. Moreover, the conditions of the uniqueness and stability of positive solutions are given by means of perturbation theory. It turns out that there exists a unique asymptotically stable positive solution under certain conditions whendis sufficiently large. Crowley-Martin functional response;bifurcation; perturbation;multiplicity;uniqueness O175.26 A 0529-6579(2017)05-0051-09 10.13471/j.cnki.acta.snus.2017.05.007 2016-09-19 國家自然科學基金(11501496,11401356);陜西省教育廳專項科研計劃(16JK1046);陜西省自然科學基礎研究計劃(2014JQ2-1003) 李海俠(1977年生), 女;研究方向偏微分方程計算及其可視化;E-mail: xiami0820@163.com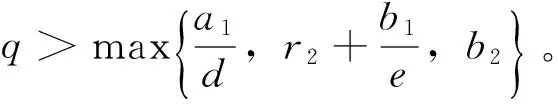


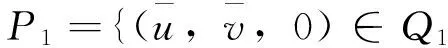




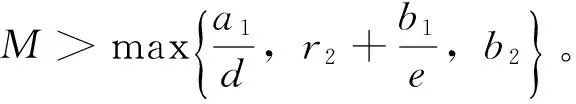
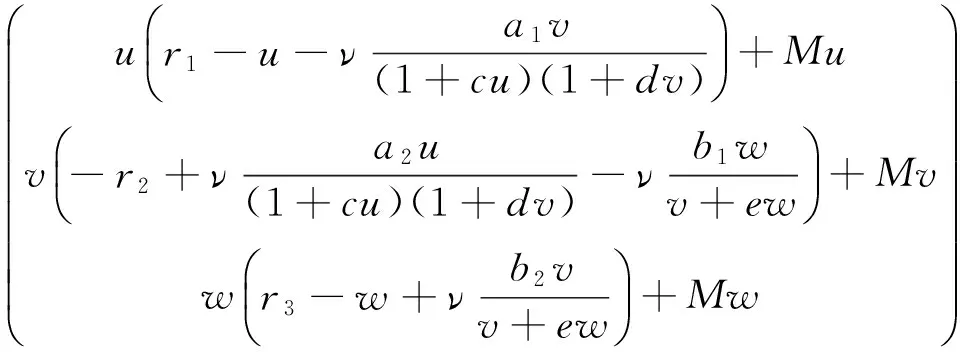
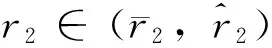

2 正解的唯一性和穩定性
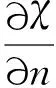


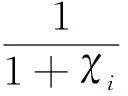
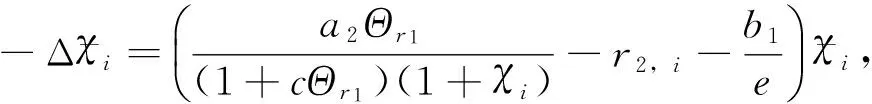
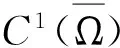
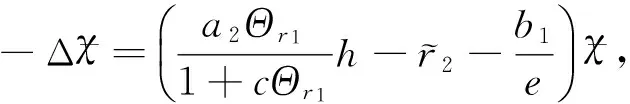
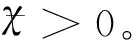

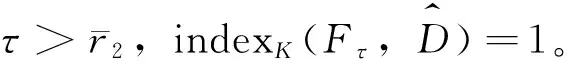
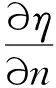

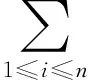
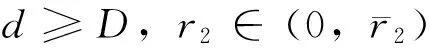


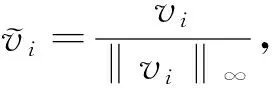
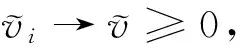

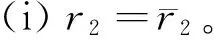
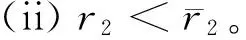


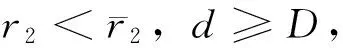
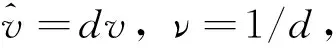
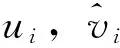
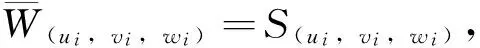
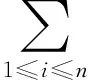
3 結 論

