能源互聯(lián)網(wǎng)下基于儲能調(diào)度及多源供能的數(shù)據(jù)中心能效優(yōu)化

孫春蕾 溫向明 路兆銘 盛萬興 曾 楠 李 洋

1(北京郵電大學信息與通信工程學院 北京 100876)

2(網(wǎng)絡(luò)體系構(gòu)建與融合北京市重點實驗室(北京郵電大學) 北京 100876)

3(先進信息北京市實驗室(北京郵電大學) 北京 100876)

4(中國電力科學研究院 北京 100192)

5 (國家電網(wǎng)公司 北京 100031)

(scl1992@bupt.edu.cn)

隨著大數(shù)據(jù)、云計算及“互聯(lián)網(wǎng)+”的發(fā)展.數(shù)據(jù)中心在數(shù)量與規(guī)模上面臨著爆發(fā)式增長.同時，數(shù)據(jù)中心能耗問題日益成為社會關(guān)注的焦點.據(jù)統(tǒng)計，2013年美國本土數(shù)據(jù)中心能耗達到了91MWh[1],到2030年數(shù)據(jù)中心的耗電量有可能突破全國用電量的20%[2].因此，數(shù)據(jù)中心的能效優(yōu)化問題變得尤為重要.目前，關(guān)于數(shù)據(jù)中心能效優(yōu)化的論文主要包括2個方面：

1) 從提高電源系統(tǒng)本身的能源轉(zhuǎn)換效率角度，例如文獻[3]和文獻[4].其中文獻[3]從提高供電系統(tǒng)電壓、電流轉(zhuǎn)換效率的角度研究數(shù)據(jù)中心能效優(yōu)化問題；文獻[4]從電池本身的物理構(gòu)造角度闡述充放電效率與循環(huán)壽命的問題.

2) 從數(shù)據(jù)中心業(yè)務(wù)負載均衡的角度，例如文獻[5-7].其根據(jù)實時電價，對分布式數(shù)據(jù)中心間的業(yè)務(wù)分配進行負載均衡，對數(shù)據(jù)中心中處于開啟狀態(tài)的服務(wù)器數(shù)量進行優(yōu)化，進而降低數(shù)據(jù)中心能源成本.

近年來，能源互聯(lián)網(wǎng)的發(fā)展為數(shù)據(jù)中心能效優(yōu)化問題提供了新的解決思路.首先，儲能系統(tǒng)在削峰填谷及提高電源系統(tǒng)穩(wěn)定性等方面的作用日益突出.其次，分布式清潔能源的發(fā)展以及售電側(cè)的放開[8-10]，為數(shù)據(jù)中心等高耗能用戶提供了多源能源選擇的可能性.因此如何在實時電價及多源供能的背景下，結(jié)合儲能時序的優(yōu)化，在降低數(shù)據(jù)中心能耗成本的同時，提高清潔能源占比是一個很有意義的問題.本文旨在從儲能、多源能源供應的角度對數(shù)據(jù)中心的能源利用效率進行優(yōu)化.本文的主要工作包括3點：

1) 引入污染指數(shù)函數(shù)，對不同清潔程度的能源進行懲罰，實現(xiàn)了對用戶節(jié)能行為的激勵，同時提高了清潔能源使用比例.對節(jié)能減排具有重要意義.

2) 通過構(gòu)建儲能操作成本以及未來潛在成本實現(xiàn)了對儲能充放電電量的時序優(yōu)化，一方面實現(xiàn)了削峰填谷，另一方面進一步降低了數(shù)據(jù)中心能源成本.

3) 構(gòu)建了基于凸二次規(guī)劃的數(shù)據(jù)中心能源成本模型，并針對相關(guān)問題的具體特點給出了求解算法.如算法1實現(xiàn)了不考慮儲能時序優(yōu)化時的能源成本最優(yōu)解的求解.

1 數(shù)據(jù)中心能源系統(tǒng)建模

1.1 數(shù)據(jù)中心能源系統(tǒng)模型簡介

數(shù)據(jù)中心的能源系統(tǒng)如圖1所示，主要包括一個智能的能源控制器、標準配比的儲能系統(tǒng)以及支持多源供應的電源系統(tǒng).式(1)給出了數(shù)據(jù)中心能源系統(tǒng)的供需平衡關(guān)系.

(1)

其中,P(t)表示當前時刻數(shù)據(jù)中心的總能耗，o(t)表示當前時刻儲能系統(tǒng)的充放電電量，qn(t)表示當前時刻第n種能源的購買量，且n∈N={1,2,…,N}.

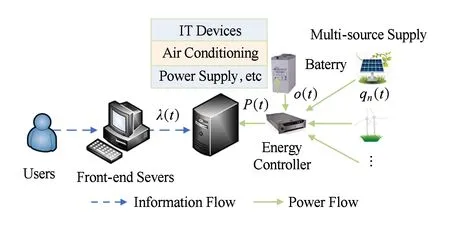
Fig. 1 Block diagram of power system for data center圖1 數(shù)據(jù)中心能源系統(tǒng)示意圖

根據(jù)文獻[11],數(shù)據(jù)中心的能耗主要包括IT設(shè)備、空調(diào)系統(tǒng)、電源、照明等幾部分.其中，與業(yè)務(wù)信息傳輸相關(guān)的通信設(shè)備能耗、與業(yè)務(wù)服務(wù)相關(guān)的服務(wù)器能耗及與服務(wù)器散熱制冷相關(guān)的空調(diào)系統(tǒng)能耗占數(shù)據(jù)中心整體能耗的80%～90%.式(2)定義了一臺內(nèi)核數(shù)為k、服務(wù)率為u、主頻為f的服務(wù)器在業(yè)務(wù)到達率為λ時的基礎(chǔ)功耗[7]：

(2)

其中,α≥3,ρ為服務(wù)器的利用率.

因此，數(shù)據(jù)中心的整體能耗如式(3)所示：

P(t)=θ1mac(t)Pserver(t)=θ1mac(t)kρfα,

(3)

其中,mac(t)為處于活躍狀態(tài)的服務(wù)器數(shù)量，θ1為服務(wù)器基礎(chǔ)功耗與數(shù)據(jù)中心整體功耗的比例.由文獻[11]可知θ1≈5.

1.2 基于污染指數(shù)的多源能源選擇模型

隨著能源互聯(lián)網(wǎng)的發(fā)展，清潔能源占比日益提高，地方上也日益涌現(xiàn)出不同規(guī)模的售電公司，打破了國家電網(wǎng)公司在售配電市場的壟斷格局，為以數(shù)據(jù)中心為代表的高能耗用戶提供了多源能源選擇的基礎(chǔ).即用戶可以根據(jù)電價、電能質(zhì)量等指標自主地從一家或多家售電企業(yè)購買電能.本文在實時電價及多源能源選擇的背景下引入污染指數(shù)的概念[12]，對數(shù)據(jù)中心的能源選擇及其成本進行建模.在降低數(shù)據(jù)中心能耗成本的同時，改善數(shù)據(jù)中心能源結(jié)構(gòu)，提高清潔能源使用率.

為了促進清潔能源的使用，污染指數(shù)函數(shù)需要滿足2個條件：1)隨著買電量的增加，污染成本逐步增加；2)隨著買電量的增加，污染邊際成本逐漸增加.因此，我們定義污染指數(shù)函數(shù)如式(4)所示：

C(qn)=γn(qn)2+βnqn,γn,βn>0,

(4)

其中，qn為第n種能源的購買量；γn和βn為第n種源的污染系數(shù).能源的清潔度越高，污染系數(shù)越小.

因此，當前時刻數(shù)據(jù)中心的買電成本如式(5)所示：

(5)

其中，pn為當前時刻第n種能源的電價.

1.3 基于預測電價的儲能時序優(yōu)化模型

根據(jù)文獻[13-14],當前時刻儲能充放電電量的優(yōu)化，必須同時考慮2個因素：1)電池充放電時的能源損耗及電池的循環(huán)使用壽命，即儲能的操作成本；2)當前時刻電池的充放電電量對未來時刻電池充放電電量的影響，即儲能的潛在成本.比如，提高當前時刻儲能系統(tǒng)的放電量，雖然可以減少當前時刻的能源購買成本，但是可能會造成未來時刻儲能系統(tǒng)充電量的增加，進而增大未來時刻能源的購買成本.

基于以上2點，如式(6)所示，構(gòu)建儲能成本：

(6)

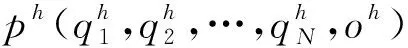
(7)

(8)

2 基于凸二次規(guī)劃的數(shù)據(jù)中心能效優(yōu)化模型

2.1 無儲能情況下的能效優(yōu)化問題

在不考慮儲能時序優(yōu)化的情況下，根據(jù)1.1節(jié)及1.2節(jié)，系統(tǒng)成本函數(shù)可表示為式(9).本文引入污染指數(shù)對每種能源的污染成本進行懲罰.一方面，在降低數(shù)據(jù)中心整體能源成本的同時，對其能源結(jié)構(gòu)進行優(yōu)化，提高清潔能源占比；另一方面，因為邊際成本隨著用電量的增加而增加，進一步促使用戶節(jié)約能源，實現(xiàn)節(jié)能減排.

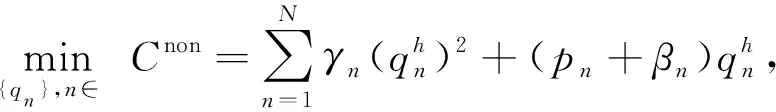
(9)

式(9)在無不等式約束下的拉格朗日對偶函數(shù)及其最優(yōu)解表示如下[15-16]，其中φ為拉格朗日因子：

(10)

(11)

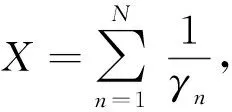
本文結(jié)合拉格朗日對偶法，提出了適應于式(9)的求解算法——算法1，并在數(shù)學上給出了解的最優(yōu)性證明，具體證明細節(jié)見附錄A.同時，本文在第4節(jié)給出該算法與內(nèi)點法等數(shù)值仿真方法的性能比較.

算法1. 最優(yōu)電量求解算法.

① 初始化相關(guān)參數(shù)及變量

② Repeat

③ 根據(jù)式(10)(11)求解拉格朗日對偶解；

④ 對拉格朗日對偶解進行修正

End If

End If

⑤ 將經(jīng)步驟④修正過的能源n剔除集合;

值得注意的是，絕大多數(shù)數(shù)據(jù)中心均配置一定規(guī)模的儲能系統(tǒng)，且本文的重點也是對有儲能配置的數(shù)據(jù)中心進行能效優(yōu)化.研究不考慮儲能時序調(diào)度下的數(shù)據(jù)中心能效優(yōu)化問題的意義在于為2.2節(jié)中的儲能策略提供對比基準.

2.2 有儲能情況下的能效優(yōu)化問題

根據(jù)第1.3節(jié)，在對有儲能時的能源成本進行建模時，除了考慮儲能對能源購買總量的影響外，還需要考慮儲能自身的操作成本以及潛在成本.式(12)給出了當前時刻基于多源能源選擇及儲能時序優(yōu)化的數(shù)據(jù)中心能源成本模型.

minC({qn},o,oH)=

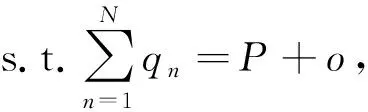
P=θ1mackρfα,

qmin n≤qn≤qmax n,

smin≤s0+o≤smax,

l=1,2,…,H,

其中,s表示儲能系統(tǒng)中的電量;smin和smax分別表示儲能系統(tǒng)中電量的下限和上限;s0表示當前時刻儲能系統(tǒng)電量的初始值.

根據(jù)觀察，式(12)的目標函數(shù)為二次冪函數(shù)，且約束條件均為線性約束.根據(jù)文獻[17-18],式(12)為典型的凸二次規(guī)劃問題，可通過內(nèi)點法、SQP等典型凸二次規(guī)劃算法求解.

3 實驗與結(jié)果

本節(jié)將對本文提出的模型進行仿真分析.為了不失一般性，我們假設(shè)數(shù)據(jù)中心可以選擇大電網(wǎng)、風能以及光伏3種不同的能源.其基礎(chǔ)電價分別為0.55CNY,0.65CNY,0.90CNY；峰谷電價調(diào)節(jié)比例分別為50%,30%,30%.其污染指數(shù)分別為γ1=0.25P,β1=0.1；γ2=0.20P,β2=0.07;γ3=0.15P,β3=0.05.

3.1 多源能源選擇仿真分析

圖2描述了污染指數(shù)對單位購電成本的影響.對于一個1 MW的數(shù)據(jù)中心，隨著購電量從0.1 MWh增加至1 MWh，其單位購電成本也從0.67元增加至0.79元.說明污染指數(shù)的引入可以通過增加高耗能用戶的平均單位能源成本，加重對高耗能行為的懲罰，從而激勵用戶節(jié)約能源，實現(xiàn)節(jié)能減排.

Fig. 2 Influence of pollution index on unit cost圖2 污染指數(shù)對單位成本的影響

圖3描述了全天0:00～24:00隨著不同能源實時電價的變化，各種能源購買量在能源購買總量中的占比.分析得出污染指數(shù)的引入可以促進多種能源的協(xié)調(diào)利用，避免了因為電價低廉而購買單一能源的情況.尤其是削減了價格低廉的火力發(fā)電購買量，相對提高了價格較高但污染成本較低的清潔能源的使用量.

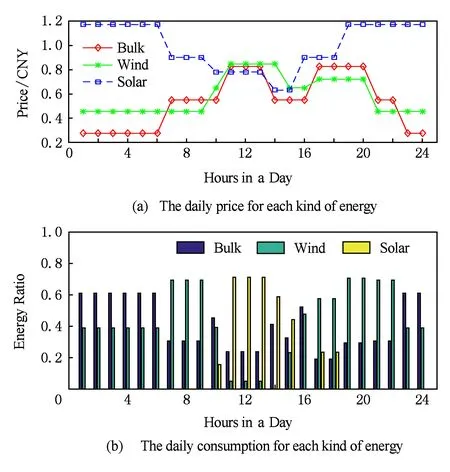
Fig. 3 Real-time price and purchase decision of each energy resource圖3 實時電價及能源購買量

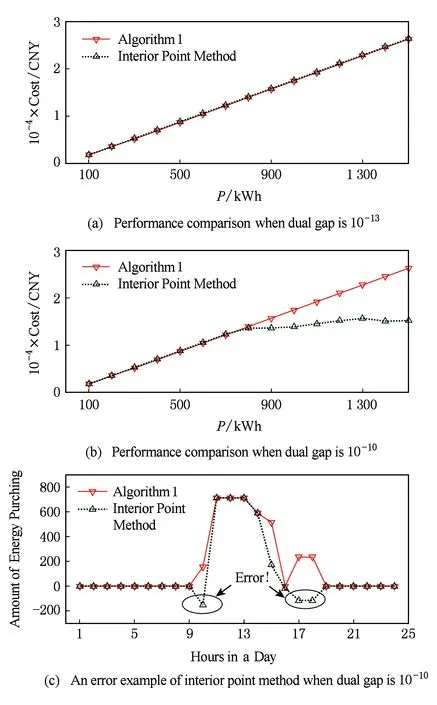
Fig. 4 Performance comparison of algorithm 1 and interior point method圖4 算法1和內(nèi)點法性能對比

圖4描述了算法1和內(nèi)點法的性能對比.當內(nèi)點法的對偶間隙精度較高時，算法1與內(nèi)點法所求解的精確度基本相同，但由表1可知，算法1的收斂速度大約是內(nèi)點法的30倍.此外，隨著內(nèi)點法對偶間隙精度的降低，算法容易出現(xiàn)明顯錯誤.圖4(c)描述了對偶間隙精度為10-10時內(nèi)點法的錯誤情況.

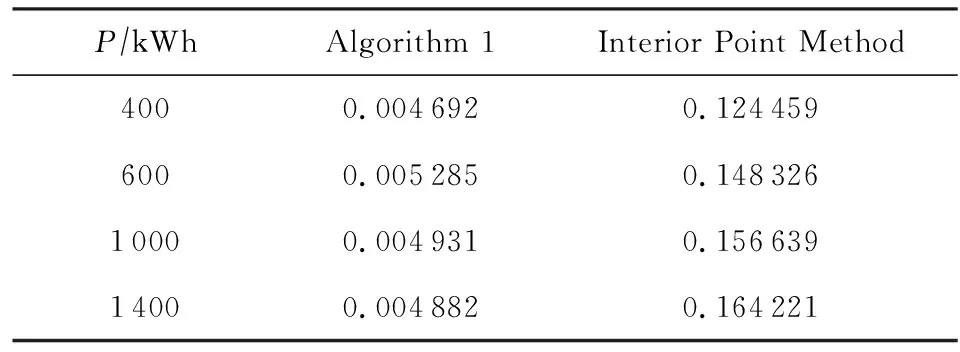
Table 1 Convergence Time of Algorithm 1 andInterior Point Method

3.2 有儲能時能源成本仿真分析

圖5描述了當前時刻儲能充放電電量對未來時刻的影響,其中d(h)=‖oh(o=o′)-oh(o=200)‖.在1 MW的數(shù)據(jù)中心中，以當前充電量為200 kWh為參考，分別給出了當前時刻充電量變?yōu)?00 kWh和400 kWh時儲能系統(tǒng)未來時刻充放電電量的變化情況.由圖5可知，當前時刻儲能充放電電量對未來6～7個小時內(nèi)的儲能充放電情況影響比較明顯.因此，仿真實驗中取H≥6即可.

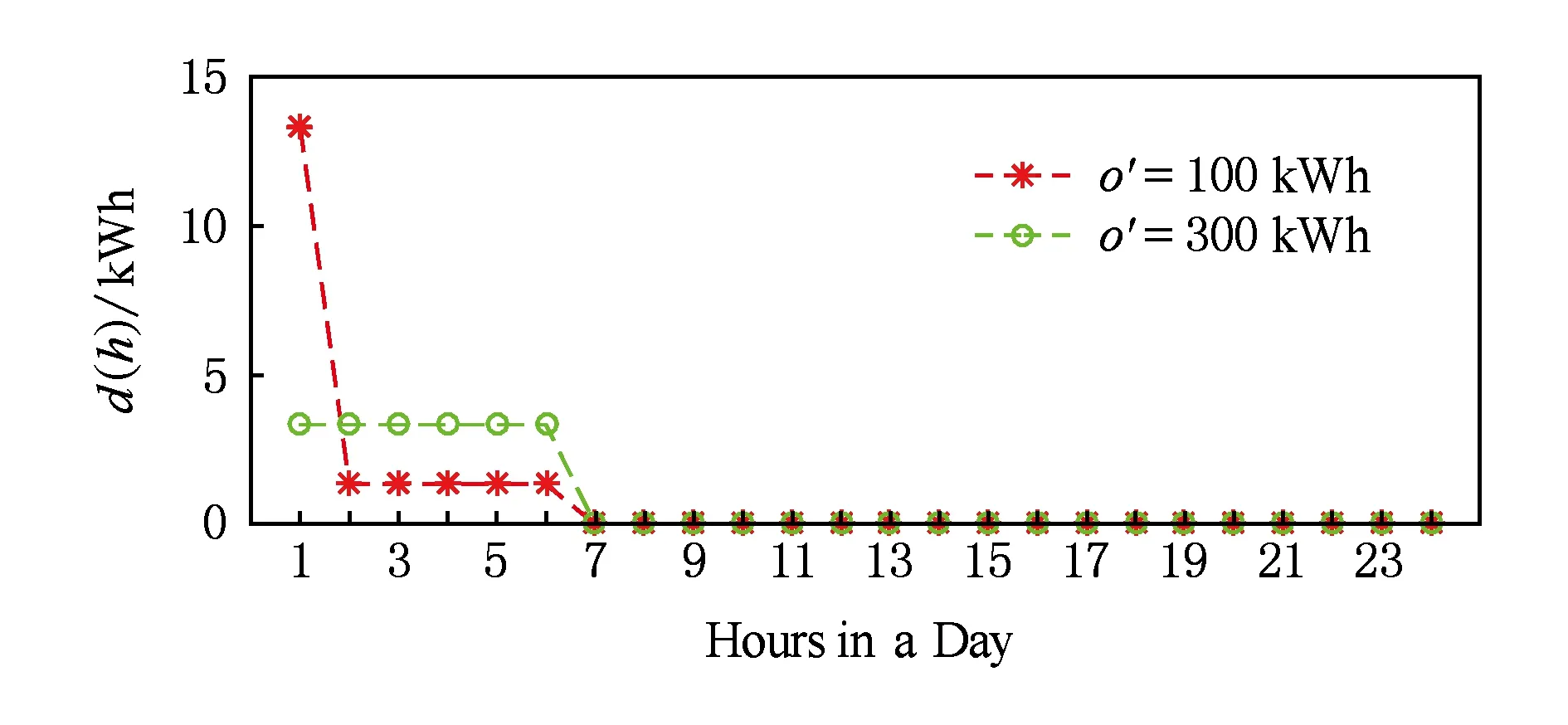
Fig. 5 Influence of present battery charging and discharging on that in future圖5 當前時刻儲能充放電電量對未來時刻的影響

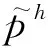
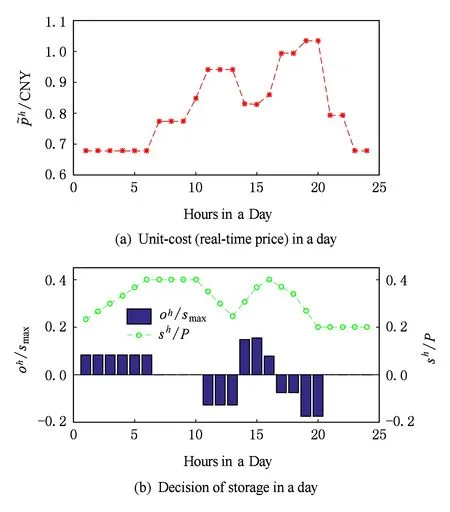
Fig. 6 Connection of battery charging and real-time price圖6 儲能充放電電量與實時電價的關(guān)系

圖7描述了數(shù)據(jù)中心配置儲能系統(tǒng)后，比未配置儲能系統(tǒng)時實現(xiàn)的成本節(jié)約量.由圖7可知，隨著數(shù)據(jù)中心規(guī)模的增大以及儲能配置容量的增加(從10%增加至40%)，其節(jié)省的成本也隨之增大.對于一個1.5 MW、儲能配比為40%的數(shù)據(jù)中心，每年可節(jié)約高達10萬元的能源成本.

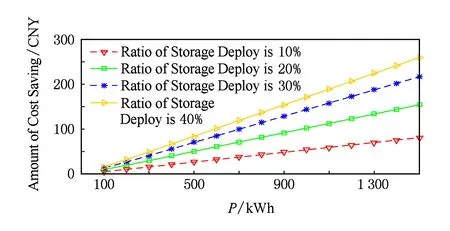
Fig. 7 Influence of storage on the economy of energy cost圖7 儲能對節(jié)約能源成本的影響

3.3 電價預測方法對能源成本的影響

在對儲能的潛在成本進行建模時，涉及到對未來時刻單位能源成本的預測.圖8描述了3種不同電價預測方法對能源成本節(jié)約量的影響.因為電價預測方法不是本文的重點，因此本文簡單地采用下文中的3種方法進行實驗仿真.結(jié)果表明，未來時刻單位能源成本預測的準確性對本文模型的性能有一定的影響.

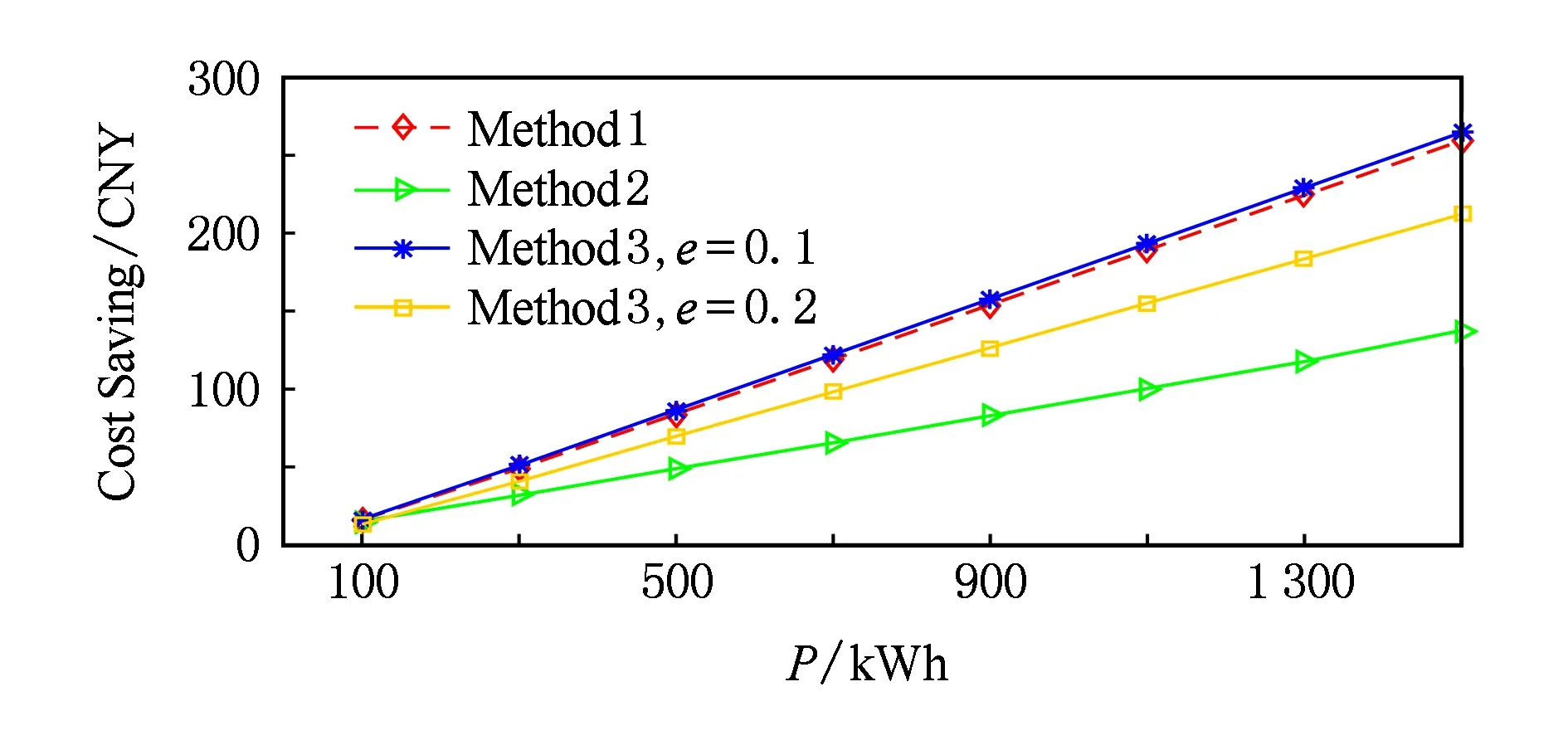
Fig. 8 Comparison of profit by different price prediction methods圖8 不同電價預測方法下能源成本節(jié)約量的對比

1) 方法1

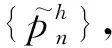
2) 方法2

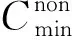
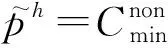
3) 方法3

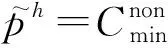
其中，e為一個很小的常數(shù).

4 總結(jié)與展望

本文主要從儲能、多源能源供應的角度對數(shù)據(jù)中心的能源成本進行了優(yōu)化.首先引入污染指數(shù)函數(shù)，對高耗能用戶及不同清潔程度的能源進行懲罰，實現(xiàn)了對用戶節(jié)能行為的激勵，同時提高了清潔能源使用比例.其次，通過構(gòu)建儲能的操作成本以及未來潛在成本實現(xiàn)了對儲能充放電電量的時序優(yōu)化.一方面實現(xiàn)了削峰填谷，另一方面進一步降低了數(shù)據(jù)中心的能源成本.最后，構(gòu)建了基于凸二次規(guī)劃的數(shù)據(jù)中心能源成本模型，并針對相關(guān)問題的具體特點給出了求解算法.仿真結(jié)果表明：隨著數(shù)據(jù)中心規(guī)模的增大以及儲能配置容量的增加，通過運用本文提出的能源成本優(yōu)化模型，其節(jié)省的成本越多.對于一個1.5 MW、儲能配比為40%的數(shù)據(jù)中心，每年可節(jié)約高達10萬元的能源成本.

本文僅僅從數(shù)據(jù)中心能源系統(tǒng)本身的角度對其能源成本進行了優(yōu)化.業(yè)務(wù)QoS保障與能源成本的綜合優(yōu)化、數(shù)據(jù)中心的最佳儲能配比、高效準確的電價預測方法等是未來的研究方向.