楔形體在波浪中自由入水的數值模擬

王 平，袁 帥，張寧川，陳偉斌，陳 元

(1.國家海洋環境監測中心，遼寧 大連 116023; 2.大連理工大學 海岸及近海工程實驗室，遼寧 大連 116024)

楔形體在波浪中自由入水的數值模擬

王 平1，袁 帥1，張寧川2，陳偉斌1，陳 元1

(1.國家海洋環境監測中心，遼寧 大連 116023; 2.大連理工大學 海岸及近海工程實驗室，遼寧 大連 116024)

物體入水時波浪的影響不可忽略，基于流體力學模型采用VOF法，并利用自定義函數，模擬了楔形體的自由入水過程；同時結合推波板原理及海綿層消波理論實現了數值水槽的造消波，完成了波浪中楔形體自由入水的模擬，計算了楔形體入水時所受的水作用力、自由液面變化及物面壓強分布等，研究了不同波高、周期以及在波浪不同位置入水時對楔形體的影響。結果表明：本文建立的數值模型可很好地模擬楔形體入水造成的射流及空泡的形成發展過程，波浪對楔形體入水的影響主要由波浪內部流場變化及表面波形決定，在波浪不同位置處入水對楔形體受力及入水形態均有較大影響。

楔形體；波浪；入水；VOF；數值模擬

入水問題廣泛存在于船舶、航空、水中兵器及儀器下水等研究領域中，物體在入水時不僅涉及較大的沖擊壓力，也會產生水體飛濺效應，且入水時間短、流場變化劇烈，實驗研究的難度較大，隨著數值方法對自由液面追蹤及動邊界處理的逐漸成熟，數值模擬已成為研究入水過程的重要方法，同時由于研究的深入及對入水壓力和姿態要求越來越嚴格，波浪對入水過程的影響已不可忽略。

數值模擬物體入水的研究較多，如Zhao[1]和Zhu[2]均基于勢流理論采用邊界元方法研究了楔形體的入水問題，但無法刻畫入水過程造成的射流影響；Arai[3]采用帶自由表面的兩相流模擬方法(VOF)模擬了二維楔、圓柱船艏的砰擊入水問題，陳宇翔[4]也采用了VOF方法對圓柱的入水過程進行了模擬，Kleefsman[5]則基于VOF法模擬了二維楔形體的自由落水問題，結果表明：VOF法可以很好地處理自由面重構等強非線性現象；Shao[6]采用了無網格的SPH法計算了物體入水的自由液面及流固相互作用等問題，很好地處理了入水時液面變形較大問題，但數值計算量較大。而波浪中的物體入水研究卻較少，其中Faltinsen[7]基于勢流邊界元理論采用附加質量法，計算了入射波對入水物體的影響，但只能給出物體所受的合力，對于其它細節卻無法給出，同時在物體完全入水時，計算結果會受到較大的影響；為此，王文華[8]基于CFD模型并采用自由液面捕捉法模擬了圓柱懸掛入水時波浪的周期性對懸繩受力的影響，但未就楔形體在波浪過程中的入水進行研究；儲慧林[9]基于Fluent的VOF法研究了魚雷入水時波浪對魚雷受力、空泡閉合等的影響，但其考慮的物體入水為勻速狀態，而實際物體在入水初期受到較大的沖擊壓力，其速度及姿態均會發生較大的改變。

基于計算流體力學模型(Fluent)，采用VOF法，并利用自定義函數，模擬了楔形體的自由入水過程。同時結合推波板原理[10]及海綿層消波理論[11]實現了數值水槽的造消波，在波浪穩定后，控制楔形體的向下運動，實現了波浪中楔形體自由入水的模擬，計算了楔形體入水時所受的水作用力，以及自由面的變化和物體表面的壓強分布等，同時研究了不同波高、周期和在波浪不同位置入水對楔形體入水的影響過程，數值結果對研究復雜海況下的物體入水問題具有一定的參考意義。

1 數學模型

1.1基本方程

對于不可壓縮流體，在直角坐標系下其運動規律可以用N-S方程來描述，包括連續性和動量方程分別為：

式中：uj為(x,y,z)三個方向上的流速分量；Fi為單位質量力沿(x,y,z)三個方向的分量；P為壓強；υt為紊流粘性系數，本文采用k-ε湍流閉合模型對其求解。

自由面追蹤采用VOF法，即通過求解單獨的動量方程和處理穿過區域的每一流體容積比來模擬兩種或多種不能混合的流體。定義體積函數αq代表第q種流體，對任一單元存在三種可能，即：αq=0表示該單元第q流體不存在；αq=1表示該單元充滿第q流體；0<αq<1表示該單元存在著流體之間的界面。

以第q流態為例，其體積函數的輸移擴散方程：

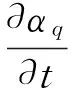
在任一單元中控制方程的特性參數是由幾種流體的組合表示，以q1和q2兩種流態為例，那么單元體的密度可以表示為式(4)，其它特性參數如粘性系數等均按此方法計算。

模型中楔形體視為剛體結構，不發生受力變形，根據牛頓第二定律，流體中運動的剛體動力學方程定義為：

(5)

式中：F、M′為物體所受力及力矩，m為物體質量，[IG]為慣性矩，VC表示物體平動速度，w表示物體角速度。

對由固體運動造成的動邊界問題則采用動網格技術，即完成每一步物體的運動狀態計算后重新劃分網格。為詳細刻畫物體入水時的射流現象，在物體周圍設置移動加密網格，該計算域網格隨物體一起下移。而物體的運動則使用六自由度模型計算，并通過自定義函數define_sdof_properties(name,prop,dt,time,dtime)來定義其質量及轉動慣量等。

數值計算中采用速度和壓力場耦合(Coupled)算法，VOF模型采用自由面重構方法來處理液面變化，湍流采用k-ε兩方程模型和壁面函數法，壓強計算采用體積力加權(Body Force Weighted)二階差分格式，密度和動量均采用二階迎風格式。

1.2數值造波與消波方法

本文根據線性造波機原理，將計算域的左邊界設置為一個運動邊界即造波板，用以模擬活塞式造波機運動，從而生成規則波。在原點設置一沖程為S、圓頻率為ω的造波機做簡諧運動，得到其水平位移和速度分別為：

得到在水深為d的波浪水槽中，產生的波面方程為：

式中：k為ω2=gktanh(kd)的正實根；kn為方程ω2=-gktanh(kd)的正實根，式右邊第二項為造波機產生的衰減立波，其隨著離造波板距離的增加而以指數型式衰減，可以忽略。剩下的第一項即為造波機產生的行進波，其波高為2S[cosh(2kd)-1]/[2kd+sinh(2kd)]，圓頻率即為ω。造波板運動由自定義函數define_cg_motion(name,dt,vel,omega,time,dtime)來定義。

為降低初始擾動，在初始2個波周期(T=2π/ω)內對造波板的運動進行平滑，具體如下：

為消除水槽前后端對波浪的反射作用，引入動量源消波法，在動量方程的右端增加一個動量衰減的源項[12]，即在水槽末端添加至少一倍于波長的消波段：

式中：μ為消波系數，沿波浪傳播方向取線性分布，-μui為消波項，在Fluent模型中由自定義函數define_source(name,c,t,dS,equ)進行添加，消波后水槽右端邊界為固壁形式。

2 數值試驗及結果分析

2.1楔形體在靜水中的入水過程

Zhao[13]曾完成了楔形體在靜水中自由入水過程的研究。依此，本文剛性楔形體的參數選擇如下：斜升角為30°，寬度為0.5 m，高度為0.29 m，質量為241 kg，長度為1.0 m，在數值計算中，初始時刻為楔形體頂點接觸平靜自由液面的瞬間，楔形體初始速度為-6.15 m/s，隨后開始自由入水。由于沖擊問題對網格要求較高，不同密度網格對計算結果的影響可能較大，因而在模擬鍥形體入水時首先要進行網格無關性驗證。設計四種不同尺度網格，分別為工況1：最小網格尺寸(楔形體處)為0.02 m，最大網格尺寸(邊界處)為0.1 m，整體網格單元數為18 653個，網格節點數為9 480個；工況2：最小和最大網格尺寸為0.01和0.07 m，單元數為40 692個，節點數為20 587個；工況3：最小和最大網格尺寸為0.01和0.05 m，單元數為74 630個，節點數為37 624個，其局部網格如圖1所示；工況4：最小和最大網格尺寸為0.005和0.03 m，單元數為268 526個，節點數為134 800個。數值計算時間步長均為0.000 1 s，利用上述四種工況計算得到楔形體入水后的垂向水動力變化對，比如圖2所示。從圖2可以看出隨著網格密度的增大垂向水動力的波動越小變化越穩定，在工況3中數值結果已較為平穩，為保證計算結果的準確性，同時減少計算量，后續入水計算選用工況3中的網格分辨率。

為分析數值模擬過程中的收斂性，圖3給出了上述工況1和工況3在初始計算時的殘差變化，其中殘差的定性收斂值為10-4，每一步的最大迭代步數為200步，由于數值計算為非穩態，因此在每一步更新時殘差均會變大，從圖3可以看出除第一步外其余每步的迭代計算殘差會很快降到10-4以下，且能量殘差(k)均在10-6以下，說明數值計算的每一步迭代均能很快達到收斂。

基于工況3數值計算得到楔形體的垂向水動力和垂向速度，與實驗結果及Kleefsman的數值結果進行對比，如圖4(a)和4(b)所示，圖中F代表楔形體受到水體的垂向水動力，V代表楔形體的垂向速度，橫坐標為時間。從圖4可知，本文數值模式很好了模擬了楔形體在入水過程中的受力及速度變化，楔形體所受的最大垂向水動力主要發生在入水初期的抨擊階段。

圖1 楔形體在靜水中自由入水的網格劃分Fig.1 Numerical grid for the free water-entry wedge

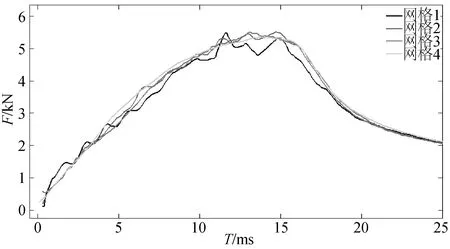
圖2 不同網格數下楔形體入水后的垂向水動力變化Fig.2 Comparison of vertical hydrodynamic force for water-entry wedge between differernt meshes

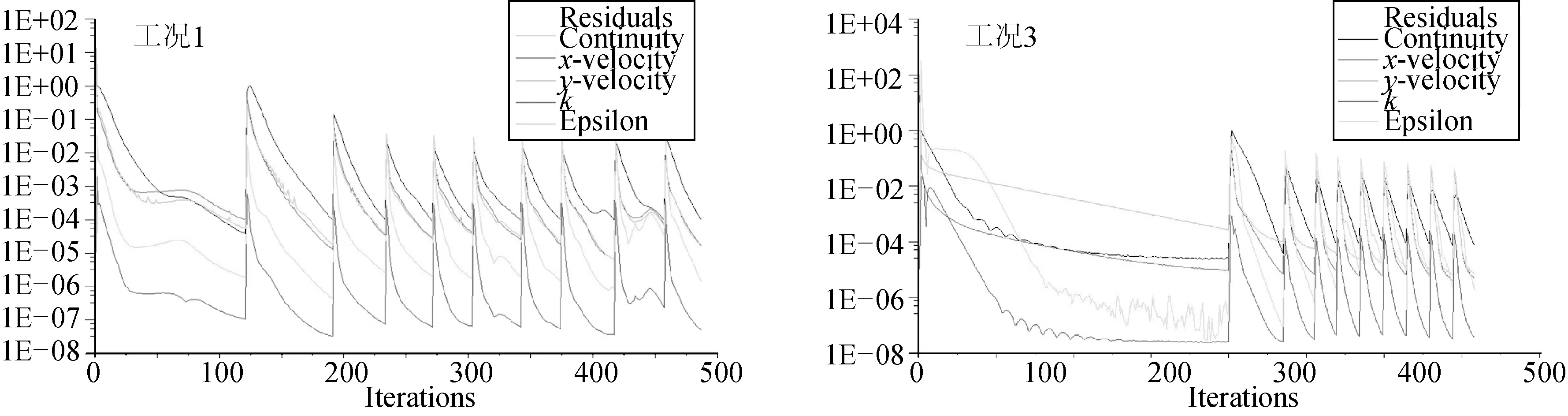
圖3 工況1和3中楔形體入水后的殘差變化Fig.3 The residual variation of the free water-entry wedge in case 1 and 3

圖4 楔形體垂向水動力和速度與實驗數據和Kleefsman結果對比Fig.4 Comparison of vertical hydrodynamic force and velocity between simulation and experiment

同時得到入水初期不同時刻的速度矢量及自由液面變化，如圖5所示。從圖5可知，楔形體入水后會對水體產生擠壓，會使得水體沿斜邊產生射流，同時在楔形體底部斜邊和自由液面之間的空氣會受到擠壓而向兩側逃逸，并在斜邊末端發生分離，從而形成一組對稱的空氣漩渦。

為描述楔形體從入水到浸沒的過程，以及楔形體兩側射流變化形態，圖6給出了從t=0 s到t=0.8 s中每隔0.1 s水體自由液面變化過程。數值結果詳細描述了從楔形體接觸水面到空泡形成再到空泡閉合的整個過程；而楔形體入水造成的兩側射流基本對稱，且在重力的作用下，射流逐漸彎曲向下，并最終融入兩側水體中。

圖5 不同時刻自由液面形狀和速度矢量Fig.5 Free surface profile and velocity vectors for free falling wedge at various water entry moments

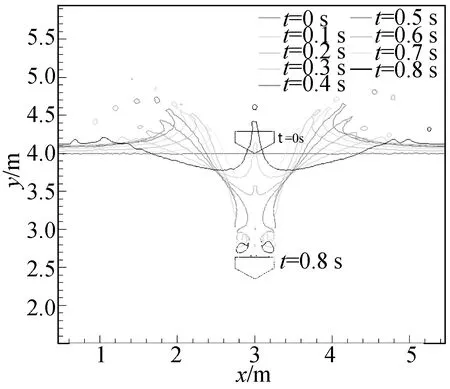
圖6 楔形體從入水到浸沒過程中自由液面變化Fig.6 Free surface profiles of the free falling wedge from water-entry and water-immersion

2.2波浪數值水槽的構建

為分析數值波浪水槽的造波功能，完成楔形體在波浪中入水的數值模擬，建立如圖7所示的200.0 m×12.0 m的數值水槽。為減少數值計算量，在楔形體入水區域采用三角形加密網格，而在其它波浪傳播區域則采用矩形網格，最小網格尺寸(楔形體附近)0.01 m，垂向最大網格尺寸0.05 m，水平向最大網格尺寸0.5 m，整體網格單元數(包括矩形和三角形)324 472個，網格節點數208 281個。水槽自左向右分別為前端緩沖區、波浪傳播區和后端消波區域，而楔形體的入水區則放在波浪傳播區域，造波板設置在水槽的左邊界上，且為坐標原點。

圖7 波浪數值水槽示意Fig.7 Sketch of Cartesian cut cell mesh and zone partition in numerical wave flume

為驗證數值水槽造消波的有效性，首先模擬波高Hs=1.0 m、周期T=4.0 s的二維規則波，不考慮楔形體的入水過程。根據線性造波機理論，得出造波板的往復運動為S=0.583 6 m、ω=1.57 s-1。

計算得到x=50、100及150 m處的波高過程線如圖8所示。從圖8可知在x=50、100及150 m處波高分別約為0.98、0.95和0.9 m，波浪在傳播過程中受粘性的影響會發生一定的衰減。圖9給出了計算區內的波面過程線和波浪內部的流場分布。從圖9可知波面過程線及波浪內的流場分布均符合線性波理論。

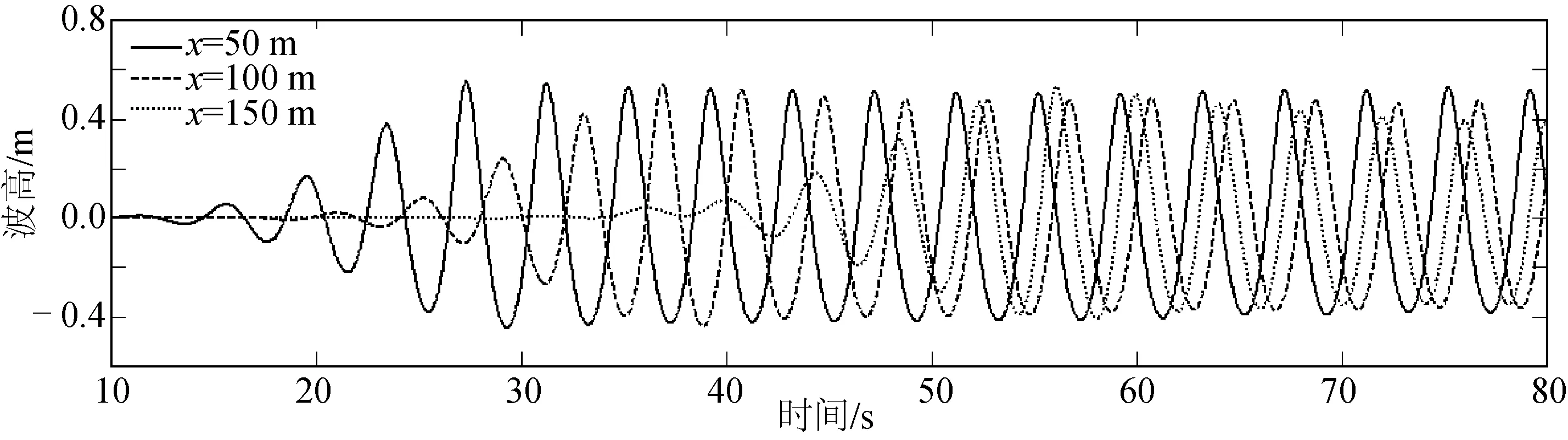
圖8 不同位置處的波面時間過程線Fig.8 Time series of wave profile at x=50 m,x=100 m,x=150 m and x=190 m

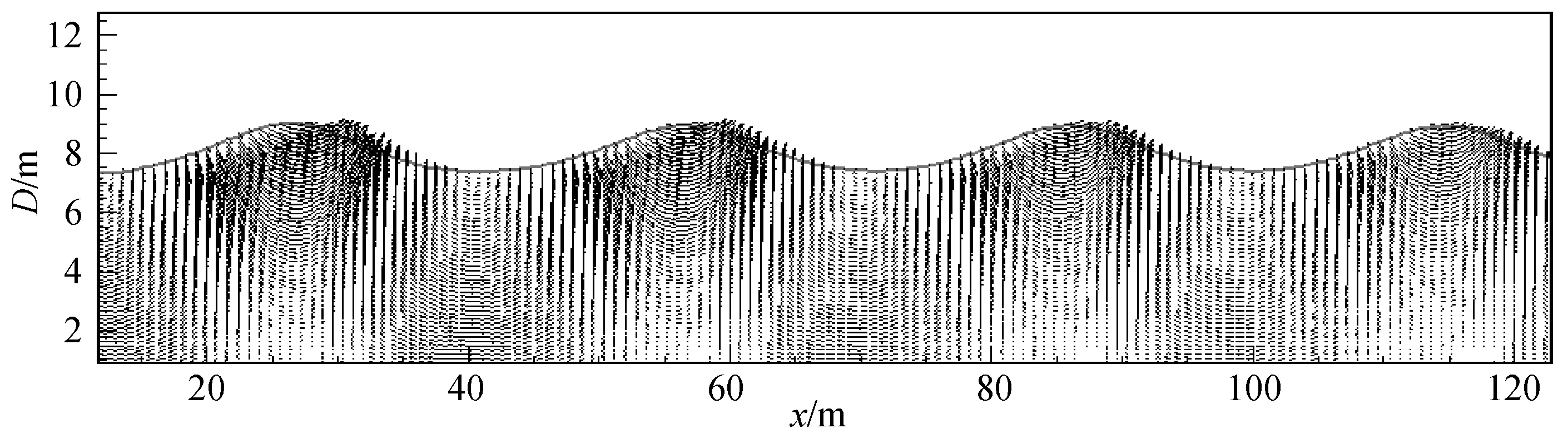
圖9 數值水槽內波浪波形及流場分布Fig.9 Free surface and velocity field in numerical flume

2.3楔形體在波浪中入水的計算

波浪數值水槽分別模擬不同波高和周期的波浪，同時設置楔形體的入水時間和入水速度，使得楔形體在波浪的波峰、平衡位置(速度向下)、平衡位置(速度向上)、波谷處入水，且入水時的速度均為-6.15 m/s，楔形體在波浪不同位置處入水示意如圖10所示。

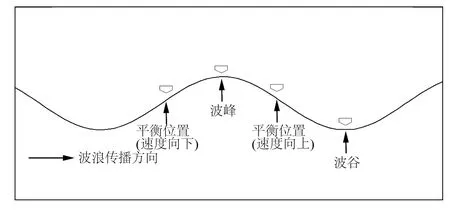
圖10 楔形體在波浪不同位置處入水示意Fig.10 Sketch of the free falling water-entry wedge in the wave

數值計算得到周期為4 s、波高不同時楔形體的垂向水動力及速度變化對比，如圖11所示，以及波高為1 m、周期不同時楔形體在波峰處入水后的垂向水動力及速度變化對比，如圖12所示。

從上述結果可以看出，楔形體在波峰處入水，隨著波高的增加，入水初期的垂向水作用力峰值會減小，而速度變化變緩，結論和文獻[14]相同；隨著周期的增大，入水初期的垂向水動力峰值略有增大，并趨近于無波浪的入水過程。

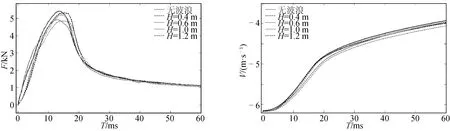
圖11 不同波高下楔形體在波峰入水時的垂向水動力及速度變化對比Fig.11 Comparison of vertical hydrodynamic force and velocity under different wave heights

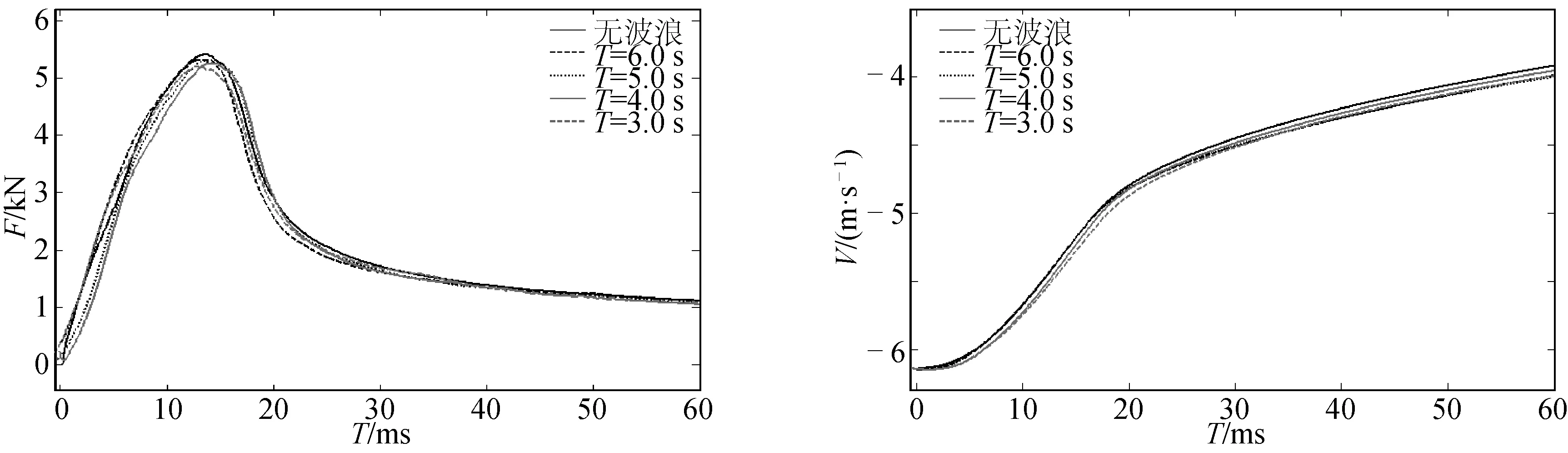
圖12 不同周期下楔形體在波峰入水時的垂向水動力及速度變化對比Fig.12 Comparison of vertical hydrodynamic force and velocity under different wave periods

同時模擬研究了楔形體在波浪Hs=1.0 m、T=1 s的波谷、平衡位置(速度向下)和平衡位置(速度向上)三種情況下入水的垂向水作用力及垂向速度變化，如圖13所示。

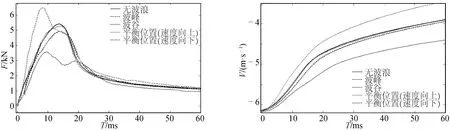
圖13 楔形體在波浪不同位置處入水的垂向水動力及速度變化對比Fig.13 Comparison of vertical hydrodynamic force and velocity under different positions

從圖13可知：楔形體在波浪平衡位置(速度向上)處入水時所受的垂向水動力峰值最大，大于無波浪情況，造成垂向速度的降低更為顯著；而在平衡位置(速度向下)處入水時初期所受的垂向水動力最小，小于無波浪情況，其速度變化更緩，且在上述兩個位置處入水時受力均出現了類似雙峰值情況；在波峰和波谷處入水受力峰值均小于無波浪情況，但較平衡位置其對峰值和垂向速度的改變均不顯著。

由于楔形體入水后的壓力變化主要發生在入水初期，其上述差異主要受波形及行進波內速度場影響，根據圖9中波浪內速度場可以看出：當波浪內流速垂直向上時，楔形體入水時所受的作用力會變大，反之則會減小；而平衡位置入水時受波形影響，楔形體兩個斜邊的入水抨擊時間會不同，進而造成楔形體受力出現雙峰值情況；而隨著波高的增大及周期的減小，行進波內的流速會逐漸增大，從而對楔形體入水的影響也越來越明顯，反之則逐漸趨近于靜水狀態下的入水過程；在波峰及波谷處由于垂向速度較小，其造成的楔形體的受力及垂向速度改變較平衡位置不明顯。

圖14(a)和圖14(b)分別給出了楔形體在波峰及平衡位置(速度向上)處入水時，從T=0 s到T=0.8 s中每隔0.1 s時水體自由液面變化過程，以及每隔0.2 s時的楔形體位置示意。同靜水中楔形體入水造成的自由液面變化(圖4)對比可知，由于波浪的作用，楔形體入水造成的射流不再呈對稱形狀；波浪會對楔形體入水后的姿態產生影響，且在波浪不同位置處入水影響也有所差異。

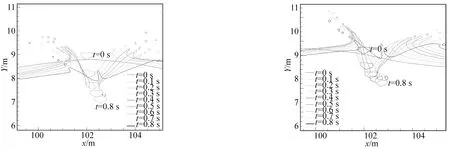
圖14 楔形體在波峰及平衡位置(速度向上)處入水時的自由液面變化Fig.14 Free surface profiles of the wedge wave-entry at wave crest and equilibrium positions

圖15和圖16分別給出楔形體在靜水及波浪的波峰、波谷、平衡位置(速度向下)和平衡位置(速度向上)中入水時斜邊壓強分布歷程。由圖可知：在靜水中楔形體斜邊上兩側的壓強始終為對稱分布，而在波浪中入水時初期斜邊壓強均為不對稱分布。在波峰處主要受波浪內水平流速的影響造成斜邊壓強的左大右?。辉谄胶馕恢?速度向下)時斜邊壓強也為左大右小，主要由于在0.02 s時，受波形的影響楔形體右側斜邊已發生入水抨擊(圖11)，而左側斜邊仍處于水體的砰擊作用中；在平衡位置(速度向上)時壓強為左小右大，也是由于波形造成斜邊浸入水體時間不同造成，而在楔形體完全浸入水中后(0.1 s后)兩斜邊壓力均基本一致。

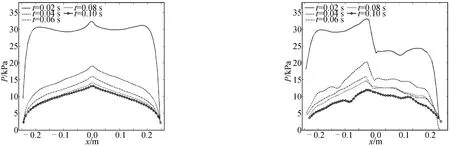
圖15 楔形體在靜水及波浪波峰處入水時斜邊壓強分布歷程Fig.15 Hypotenuse pressure distribution of the wedge wave-entry at still wave and wave crest

圖16 楔形體在波浪平衡位置(速度向下、速度向上)處入水時斜邊壓強分布歷程Fig.16 Hypotenuse pressure distribution of the wedge wave-entry at different equilibrium positions

3 結 語

基于計算流體力學模型(Fluent)，采用VOF法并利用動網格技術及自定義函數驗證了楔形體的自由入水過程，同時利用數值造消波方法模擬了楔形體在波浪中的入水過程，研究了波浪對楔形體入水初期的沖擊壓力、速度變化的影響，以及在波浪中不同位置入水時對入水壓力、斜邊壓強分布以及入水姿態變化的影響。

本文建立的入水模型可較好地模擬楔形體入水造成的射流及空泡的形成發展過程，而波浪對楔形體入水的影響主要由波浪內部流場變化及表面波形決定，結論符合之前的研究成果，數值方法及結論對復雜海況下的海洋構件入水具有一定的參考意義，由于計算量的限制，本文并未考慮三維實際情況，后續研究應予以關注。

[1] ZHAO R,FALTINSEN O M.Water-entry of two-dimensional bodies [J].Journal of Fluid Mechanics,1993,246: 593-612.

[2] ZHU X Y,FALTINSEN O M,HU C H.Water entry and exit of a horizontal circular cylinder [J].Journal of Offshore Mechanics and Arctic Engineering,2007,129:253-264.

[3] ARAI M,CHEN L Y,INOUE Y.A computing method for the analysis of water impact of arbitrary shaped bodies [J].Journal of Computational Physics,1981,39:201-225.

[4] 陳宇翔，郜冶，劉乾坤.應用VOF方法的水平圓柱入水數值模擬[J].哈爾濱工程大學學報,2011,11(32): 1 439-1 442.(CHEN Y X,GAO Y,LIU Q K.Numerical simulation of water-entry in a horizontal circular cylinder using the volume of fluid (VOF) method [J].Journal of Harbin Engineering University,2011,32(11): 1 439-1 442.(in Chinese))

[5] KLEEFSMAN K M T,FEKKEN G,VELDMAN A E P,et al.A volume of fluid based simulation method for wave impact problems [J].Journal of Computational Physics,2005,206: 363-393.

[6] SHAO S D.Incompressible SPH simulation of water entry of a free-falling object [J].Int.J.Numer.Meth.Fluids,2009,59: 91-115.

[7] FALTINSEN O M.Sea loads on ships and offshore structures [M].UK: Cambridge University Press,1990.

[8] 王文華,王言英.圓柱在波浪中入水的數值模擬[J].上海交通大學學報,2010,10(40): 1 393-1 399.(WANG W H,WANG Y Y.Numerical study on cylinder entering water in wave [J].Journal of Shanghai Jiaotong University,2010,44(10): 1 393-1 399.(in Chinese))

[9] 儲慧林.魚雷在波浪中入水的數值模擬[D].鎮江: 江蘇科技大學,2014.(CHU H L.Numerical simulation of torpedo entering water in wave [D].Zhenjiang: Jiangsu University of Science and Technology,2014.(in Chinese))

[10] LARSEN J,DANCY H.Open boundaries in short wave simulations—a new approach [J].Coastal Engimeering,1983,7(3): 285-297.

[11] 陶建華.水波的數值模擬[M].天津: 天津大學出版社,2005.(TAO J H.Numerical simulation of water waves [M].Tianjin: Tianjin University Press,2005.(in Chinese))

[12] 王鵬,孫大鵬,吳浩.海堤上波浪爬高和越浪分析[J].海洋工程,2011,29(4):97-107.(WANG Peng,SUN Dapeng,WU Hao.Numerical simulation of wave runup and overtopping over seawalls [J].The Ocean Engineering,2011,29(4):19-107.(in Chinese))

[13] ZHAO R,FALTINSEN O M,AARSNES J.Water entry of arbitrary with and without flow separation[C]//Proceedings of the 2-d Sections 21st Symposium on Naval Hydrodynamics.1997.

[14] 王文華.物體入水問題的分析研究及其在船舶與海洋工程中的應用[D].大連: 大連理工大學,2010.(WANG W H.Analysis and research on water entry problem and its application in ship and ocean engineering [D].Dalian: Dalian University of Technology,2010.(in Chinese))

Numerical study of the free water-entry wedge in wave

WANG Ping1,YUAN Shuai1,ZHANG Ningchuan2,CHEN Weibin1,CHEN Yuan1

(1.National Marine Environmental Monitoring Center,Dalian 116023,China; 2.Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

Wave impact in body water-entry cannot be ignored.Based on the hydrodynamic model,the free falling wedge water-entry cases are simulated by using the volume of fluid (VOF) method and user-defined functions.Considering the push-wave plate principle with sponge layer theory,the numerical wave flume was built.The free falling wedge in wave water-entry case was simulated,and the vertical hydrodynamic force,velocity and pressure distributions of the wedge were computed.The influence of different wave heights,wave periods and positions on wedge water-entry was also studied.Numerical results show that the free surface profile and bubble development of wedge water-entry can be simulated accurately by the module.The influence of wave on wedge water-entry was decided by the free surface and velocity field in wave flume,and the water-entry positions in wave flume had a greater impact on the wedge force and form after entering the water.

wedge; wave; water-entry; the volume of fluid (VOF) method; numerical simulation

P751

A

10.16483/j.issn.1005-9865.2017.05.005

1005-9865(2017)05-0042-09

2016-09-22

國家自然科學基金(51709054)；海洋公益性行業科研專項資助項目(201405025；201505019)

王 平(1988-)，男，安徽人，助理研究員，從事近岸動力學研究。