三塔斜拉橋的動力特性研究
楊海濤
(山西省長治公路管理段,山西 長治 046000)
斜拉橋具有很強的跨越能力,且具有結構受力合理,施工技術成熟的優點。在方案對比階段相對連續剛構及懸索橋而言具有很強的競爭力。隨著我國橋梁建設中對結構的美觀要求越來越高,斜拉橋索塔形式也越來越多樣化[1]。在建設工程中常見的斜拉橋索塔形式有A形、門式、柱式、倒Y形及菱形等,本橋采用的海豚形索塔在國內的斜拉橋中尚屬首次。而索塔的結構形式對斜拉橋動力特性有直接的影響。因此,對該種索塔的斜拉橋動力特性進行分析是十分必要的。
1 工程概況
本橋采用三塔六跨鋼箱梁平行單索面的結構形式,其跨徑布設為:110+129+258+258+129+110=994 m;主梁采用大懸臂倒梯形整體式鋼箱梁,梁高4.5 m;3個索塔外輪廓造型一致,均為海豚型造型。大橋的橋型布置圖見圖1,索塔一般構造圖見圖2。主副塔均為圓曲線的雙曲海豚塔,主塔最低端的部分采用的是鋼混結構,索塔的其他部分采用鋼結構,該索塔為鋼混組合結構。主塔為直線,副塔為圓曲線;海豚塔采用鋼結構。
該橋結構體系為三塔六跨的半漂浮體系,在豎向主梁與主塔、橋墩之間均設置拉壓球形鋼支座;在縱向主梁與主塔、橋墩之間設置阻尼裝置;在橫向1號墩、3號索塔、5號索塔、7號墩處布設橫向抗風支座;4號索塔處布設阻尼裝置;2號墩、6號墩設置滑動支座。
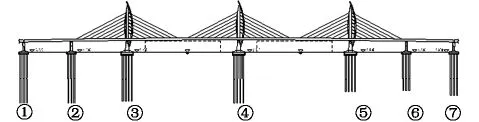
圖1 橋型布置圖
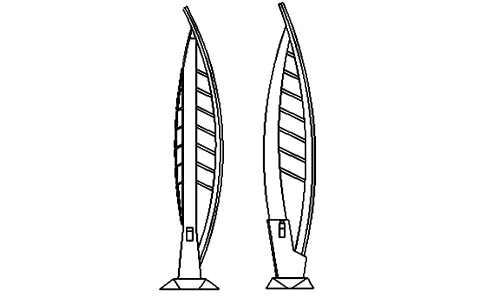
圖2 索塔構造圖
2 斜拉橋的有限元模型
眾所周知,橋梁結構的動力響應受外界環境因素的作用以及結構本身所固有的動力特性的影響。因此分析結構在外部作用下(如地震、風等因素)的結構響應,首先應先對結構的動力特性進行計算分析[2-3]。
結構動力特性主要由結構的固有頻率和結構的振型,以及結構的阻尼3部分組成,它們均是結構自身所具有的屬性。主梁的截面特性、主塔和主梁剛度的比值、主塔與主梁的連接方式、斜拉索的空間布設形式、輔助墩數量及其位置等多種因素對斜拉橋的動力性能的影響都很大[4-5]。
2.1 空間有限元模型的建立[6]
結構ANSYS模型如圖3所示。主梁和橋塔采用Beam4單元進行模擬,根據實際截面特性和剛度將主梁簡化為單主梁模型,對于質量系統的模擬是將其主梁的質量分配到主梁單元的兩端節點上,其中集中質量矩用來考慮主梁的扭轉慣矩,其他的附屬構造等通過集中質量元來模擬其對主梁平動質量和轉動慣量;用Link10單元對斜拉索進行模擬,并采用Ernst公式對斜拉索的垂度效應進行修正[7],以確保拉索模擬的精確性;用軟件中的耦合功能,采用主從節點連接的方式來模擬結構中的固定支座、橫向抗風支座、滑動支座等邊界條件,其他的自由度關系用節點耦合進行模擬。
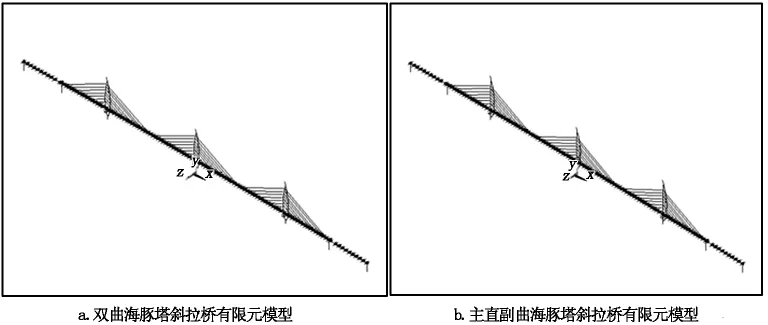
圖3 結構計算分析有限元模型
2.2 動力特性分析基本方程[8]
斜拉橋的結構體系具有質量和剛度連續分布的特點,且為多自由度體系,根據上述的有限元計算模型,對該橋的不同結構部分進行相應的簡化處理后,將結構離散成具有有限自由度的有限元計算模型。阻尼對結構自振特性影響不大,在計算結構振型和固有頻率時可不考慮阻尼的影響[4]。假設結構的自由度為n,則該體系的自由振動可用式(1)來表示[9]:
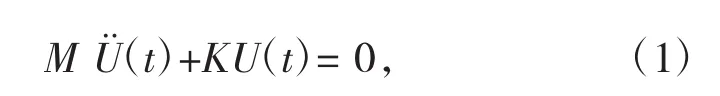
式(1)的特征方程可表示為:

由于位移是任意的,應滿足:

由式(3)可求得結構的n階自振頻率,然后將自振頻率代入式(2)即可得到相應的振型或固有模態。
結構動力分析求解方法眾多,本文采用改進的經典Lanczos方法(Block Lanczos)方法求解系統的特征值問題[10]。
2.3 橋塔對結構動力特性的影響
在分析上述兩種橋塔模型的基礎上,分別計算得到雙曲海豚塔和單直單曲海豚塔下斜拉橋的自振特性結果,兩種塔形前15階的結構自振頻率與模態分別如表1所示。
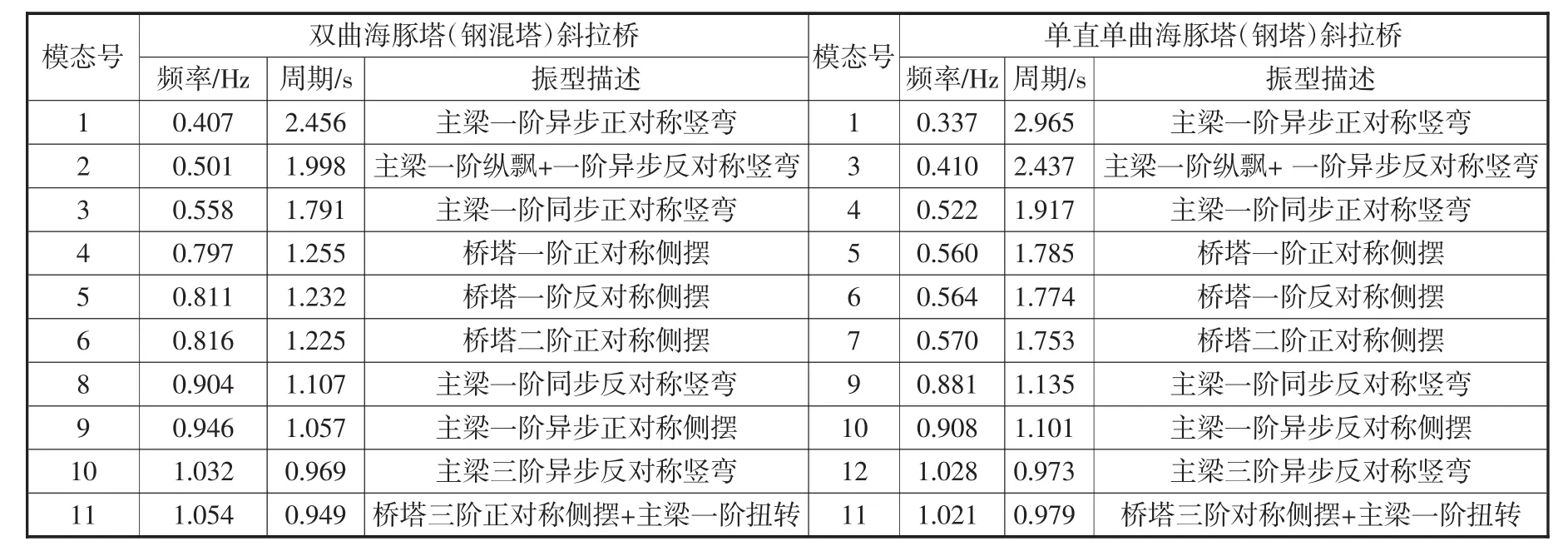
表1 自振頻率和模態對比表
在本文中僅給出了雙曲海豚塔(鋼混結構)斜拉橋的第 1、2、3、8、9、11 階的自振振型圖(圖 4)以及主直副曲塔(鋼結構)斜拉橋的第 1、3、4、9、10、11階的自振振型圖(圖5)。

圖4 雙曲海豚塔斜拉橋振型圖


圖5 主直副曲海豚塔斜拉橋振型圖
通過對表1、圖4、圖5進行分析可以得到以下的幾點結論:
a)上述兩種海豚塔的斜拉橋,其振型模態大體相同,但相應振型的頻率卻相差較大。兩種索塔形式的基本振型都是一階異步正對稱豎彎,一階豎彎對斜拉橋的地震作用響應和抗風性能有很大的影響,同時對車輛的行車舒適度來說也是非常重要的。在文中,雙曲海豚塔斜拉橋的主梁一階異步正對稱豎彎、一階異步反對稱豎彎、一階同步正對稱豎彎、一階同步反對稱豎彎出現在第1、2、3和8階模態,頻率分別是 0.407 Hz、0.501 Hz、0.558 Hz和 0.904 Hz,與其對應主直副曲海豚塔斜拉橋的主梁一階異步正對稱豎彎、一階異步反對稱豎彎、一階同步正對稱豎彎、一階同步反對稱豎彎出現在第1、3、4和9階,頻率分別為 0.337 Hz、0.410 Hz、0.522 Hz和 0.881 Hz。可以看出兩種結構的豎向剛度在一階異步正對稱豎彎、一階異步反對稱豎彎和一階同步正對稱豎彎振型中相差較大,并且雙曲海豚塔斜拉橋的豎向剛度較主直副曲海豚塔斜拉橋的大,而在一階同步反對稱豎彎中,兩種結構的豎向剛度相近。
b)順橋向的縱向漂移對主塔順橋向地震反應的貢獻占絕對的優勢,雙曲、主直副曲海豚塔斜拉橋的縱向漂移分別出現在第2和第3階模態,其頻率分別為0.501 Hz和0.410 Hz,并且耦合主梁的豎彎,振型比較復雜。
c)雙曲、主直副曲海豚塔斜拉橋的主梁一階側彎分別出現在第9和第10階模態,其頻率分別為0.946 Hz和0.908 Hz,兩者相差4.02%,從而表明索塔的形式對主梁側彎剛度影響不大。
d)文中,雙曲海豚塔斜拉橋主塔一階正對稱側擺(對稱橫橋向振動)和一階反對稱側擺(反對稱橫橋向振動)的振動頻率分別為0.797 Hz和0.811 Hz,相對應的主直副曲海豚塔的頻率分別為0.560 Hz和0.564 Hz,兩者的差別分別為29.7%和30.5%,結論表明雙曲海豚塔的橫向剛度高,抵抗橫向變形能力強。
e)在斜拉橋的顫振中主要的振型就是扭轉振型,因此分析斜拉橋的顫振臨界風速時,結構一階扭轉頻率必須足夠重視。扭轉頻率與顫振臨界風速基本上呈線性關系,也就是說扭轉頻率越高,顫振臨界風速也就越大。雙曲海豚塔和主直副曲海豚塔斜拉橋兩種結構形式的主梁一階扭轉振型均出現在第11階模態,其頻率大小分別為1.054 Hz和1.021 Hz,其振型比較復雜,為主梁扭轉耦合橋塔的彎曲。
3 結論
分析結果表明大跨度斜拉橋的剛度較小,自振周期較長,基頻較低,相鄰的頻率相差較小,模態比較密集。
通過對兩種不同索塔斜拉橋自振特性的分析對比,發現兩種不同索塔結構斜拉橋的振型基本相同;但對于相同的振型,雙曲海豚塔斜拉橋的頻率比單直單曲海豚塔斜拉橋的大,特別是在低階模態下,兩者差異很大;但在高階模態下,兩者的頻率非常接近。
通過動力特性分析可以為結構抗風性能和抗震性能研究提供必要的基礎,為結構的合理選型提供基本的資料。若要確定結構的抗風性能和抗震性能,還需進一步進行風洞試驗和抗震驗算,并應根據試驗及計算結果,采取相應的措施進行預防。

