黏性邊界層網(wǎng)格自動(dòng)生成1)
甘洋科 劉劍飛
(北京大學(xué)工學(xué)院力學(xué)與工程科學(xué)系,北京100871)
黏性邊界層網(wǎng)格自動(dòng)生成1)
甘洋科 劉劍飛2)
(北京大學(xué)工學(xué)院力學(xué)與工程科學(xué)系,北京100871)
高雷諾數(shù)黏性流動(dòng)在壁面附近存在邊界層,在計(jì)算模擬中自動(dòng)生成可靠且有效的計(jì)算網(wǎng)格仍然是計(jì)算流體力學(xué)存在的瓶頸.三棱柱/四面體混合網(wǎng)格技術(shù)在一定程度上緩解了這個(gè)困難.然而,對(duì)于復(fù)雜外形的情況,在邊界層內(nèi)自動(dòng)高效生成高質(zhì)量的三棱柱單元仍然十分困難.常用的層推進(jìn)法在凹凸區(qū)域及角點(diǎn)處生成的邊界層網(wǎng)格單元質(zhì)量較差,邊界層網(wǎng)格最外層尺寸不均勻.針對(duì)這些問題,發(fā)展了一種黏性邊界層網(wǎng)格自動(dòng)生成方法,通過頂點(diǎn)周圍邊的二面角識(shí)別物面網(wǎng)格特征確定多生長方向,預(yù)估并調(diào)整生長高度處理相交情況.同時(shí)提出一種三維前沿尺寸調(diào)節(jié)方式,提高了邊界層網(wǎng)格單元的正交性,保證了邊界層網(wǎng)格與遠(yuǎn)場網(wǎng)格尺寸的光滑過渡.通過ONERA M6翼型以及帶發(fā)動(dòng)機(jī)短艙的DLR-F6翼身組合體等外形的網(wǎng)格生成實(shí)例及繞流數(shù)值模擬,將計(jì)算值與標(biāo)準(zhǔn)實(shí)驗(yàn)值進(jìn)行對(duì)比,結(jié)果表明:該方法能夠自動(dòng)高效地生成滿足數(shù)值計(jì)算需求的混合網(wǎng)格.
邊界層網(wǎng)格,生長法向,特征邊,相交,尺寸調(diào)節(jié)
引言
近年來,計(jì)算流體力學(xué)成為學(xué)術(shù)界研究的熱點(diǎn),在航空航天、汽車、熱能動(dòng)力等工程領(lǐng)域都有著重要的地位,廣泛用于設(shè)計(jì)、分析和優(yōu)化.在計(jì)算流體力學(xué)模擬中,需要借助計(jì)算機(jī)數(shù)值求解物理量的控制方程.當(dāng)前主要采用的計(jì)算方法,包括有限差分法、有限體積法、有限元法等,都需要對(duì)計(jì)算區(qū)域進(jìn)行網(wǎng)格劃分,進(jìn)而在網(wǎng)格單元節(jié)點(diǎn)上離散求解偏微分方程.30多年來,盡管計(jì)算流體力學(xué)取得了很大的成就,網(wǎng)格生成依然是需要解決的關(guān)鍵問題之一.大批商業(yè)網(wǎng)格生成軟件,包括Gambit,Gridgen以及ANSYS ICEM-CFD等,雖然具有功能全面、使用方便、技術(shù)服務(wù)好等優(yōu)點(diǎn),但在生成含邊界層網(wǎng)格時(shí)的自動(dòng)性及可靠性較差,對(duì)于復(fù)雜外形需要大量手工操作,有時(shí)甚至無法生成.高雷諾數(shù)黏性流動(dòng)中不能自動(dòng)生成可靠且有效的網(wǎng)格仍然是計(jì)算流體力學(xué)中的瓶頸問題.
邊界層是流體運(yùn)動(dòng)中貼近壁面的薄層,其厚度與物體特征尺寸的比值為一個(gè)小量,通常小于千分之一.如果采用各向同性網(wǎng)格,則生成的邊界層網(wǎng)格單元數(shù)量巨大,大大提高了計(jì)算的代價(jià),對(duì)于大規(guī)模的復(fù)雜問題,其計(jì)算代價(jià)是目前工程上不能接受的.而如果計(jì)算域都采用大長寬比的各向異性單元?jiǎng)t會(huì)得到質(zhì)量很差的數(shù)值解[1].因此,邊界層網(wǎng)格生成的難點(diǎn)在于如何用盡可能少的網(wǎng)格單元達(dá)到捕捉層內(nèi)流動(dòng)特性的目的.
三維黏性混合網(wǎng)格策略,即在邊界層內(nèi)生成高質(zhì)量的半結(jié)構(gòu)化三棱柱單元而在其他遠(yuǎn)場區(qū)域生成各向同性的四面體網(wǎng)格單元,是目前最常用的方法,這種方法兼具結(jié)構(gòu)網(wǎng)格和非結(jié)構(gòu)網(wǎng)格的優(yōu)點(diǎn).Pirzadeh[2]提出的層推進(jìn)法(advancing layer method)是其中最具影響的一種.層推進(jìn)方法從需要生長邊界層的表面三角網(wǎng)格出發(fā),沿通過表面頂點(diǎn)的某一個(gè)方向布置各向異性網(wǎng)格的節(jié)點(diǎn),然后根據(jù)表面網(wǎng)格的拓?fù)潢P(guān)系連接這些布置的節(jié)點(diǎn)來生成一層一層的三棱柱單元,有時(shí)由于求解器的原因,三棱柱單元可以轉(zhuǎn)化為四面體,如圖1所示.
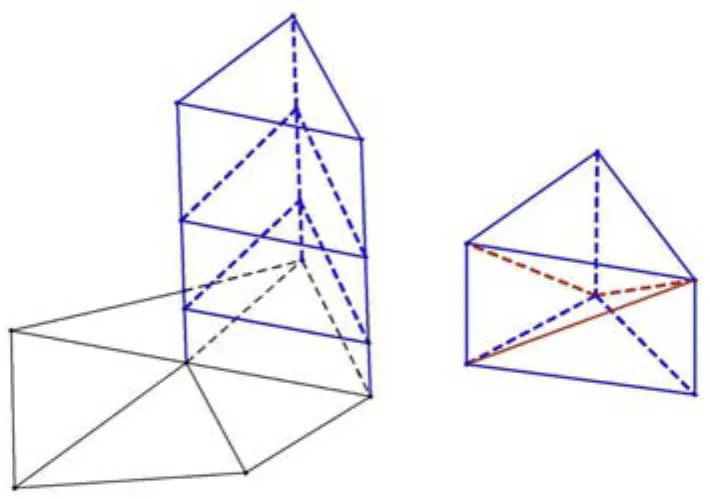
圖1 三棱柱單元生長示意圖Fig.1 Prism elements growing example
圍繞層推進(jìn)法,很多學(xué)者做了不同程度的改進(jìn),Kallingderis等[3]改進(jìn)了推進(jìn)向量的求法,提出了可見區(qū)域的概念,利用該方法求得的向量可以保證生成的單元都有正的體積.L¨ohner[4]提出了連接模型邊界上生成的半結(jié)構(gòu)化網(wǎng)格與其他區(qū)域生成的各向同性網(wǎng)格的方法,在半結(jié)構(gòu)化邊界層網(wǎng)格生成過程中,檢測形狀差,反轉(zhuǎn)、相交、尺寸不適合的單元,將相應(yīng)的單元?jiǎng)h除.Aubry等[5]提出了一種求節(jié)點(diǎn)法向的方法,并將其用于表面各向異性網(wǎng)格的生成[67],最近又利用Voronoi圖來確定非流形角點(diǎn)處的生長法向,進(jìn)而更好地生成邊界層網(wǎng)格,并集成到軟件中[8].Connell等[9]實(shí)現(xiàn)了全四面體黏性網(wǎng)格的生成,在確保相容性的前提下將三棱柱單元全部轉(zhuǎn)化為四面體單元,通過刪除單元的方式處理相交問題.Garimella等[10]引進(jìn)多生長方向,提高了非流形角點(diǎn)處的單元正交性及單元質(zhì)量,提出采用收縮、平滑、裁剪等操作處理層推進(jìn)過程中的單元自交及前沿相交情況.Athanasiadis等[1112]則提出了構(gòu)造虛擬點(diǎn)來實(shí)現(xiàn)多法向生長及法向融合操作,提高了凹凸區(qū)域黏性網(wǎng)格的正交性及結(jié)構(gòu)化特性.Sharov等[13]通過生成各向異性的表面網(wǎng)格來適應(yīng)表面凹凸區(qū)域的半結(jié)構(gòu)化黏性網(wǎng)格生成.王剛等[1415]在這方面做了一些工作,將層推進(jìn)方法應(yīng)用到黏性網(wǎng)格生成.陳建軍等[16]也在已有的研究基礎(chǔ)上,集成各種處理方法,發(fā)展了一套混合網(wǎng)格生成程序.
以上所述的方法,在出現(xiàn)相交情況的時(shí)候采用刪除單元或停止推進(jìn)的方式進(jìn)行處理,這樣會(huì)導(dǎo)致各向同性網(wǎng)格生成器的初始表面網(wǎng)格尺寸不均勻,存在長寬比很大的狹長單元,不利于各向同性網(wǎng)格的生成;同時(shí)邊界層網(wǎng)格的層狀結(jié)構(gòu)也會(huì)破壞.另外,該方法在凹凸脊及角點(diǎn)等幾何特征處需要特殊處理,現(xiàn)有的處理方法都會(huì)產(chǎn)生一定的問題,尚未合理地解決通用性的問題.
除了層推進(jìn)方法,一些學(xué)者也提出了其他方法.Dyedov等[17]將偏移面(face o ff setting)方法[18]應(yīng)用到黏性混合網(wǎng)格生成中,考慮面追蹤,并直接推進(jìn)表面三角形單元,事先確定推進(jìn)距離的上限,避免相交檢測,并提出采用變分優(yōu)化的方法對(duì)三棱柱網(wǎng)格進(jìn)行質(zhì)量改善,該方法通過求解拉格朗日演化方程的方式來生成三棱柱邊界層網(wǎng)格,并將該混合網(wǎng)格生成方法應(yīng)用到生物力學(xué)計(jì)算中,取得了一定效果.
與層推進(jìn)方法不同,Ito等[19]以及Alauzet等[20]發(fā)展了一種黏性混合網(wǎng)格的生成方法,先生成全域的非結(jié)構(gòu)各向同性網(wǎng)格,然后采用擠壓內(nèi)部網(wǎng)格的方式生長邊界層半結(jié)構(gòu)化網(wǎng)格.前者不改變各向同性網(wǎng)格的拓?fù)浣Y(jié)構(gòu),后者結(jié)合拓?fù)淇勺兙W(wǎng)格變形方法.該方法可以避免網(wǎng)格生長過程中的相交檢測,但受限于網(wǎng)格變形技術(shù),由于網(wǎng)格變形能力有限,在凹角點(diǎn)區(qū)域可以出現(xiàn)單元反轉(zhuǎn)的現(xiàn)象,同時(shí)由于擠壓,內(nèi)部非結(jié)構(gòu)網(wǎng)格的質(zhì)量下降,影響計(jì)算的精度.
張來平等[2123]在生成壁面三棱柱網(wǎng)格方面發(fā)展了一種聚合的方法,將物面附近各向異性的四面體單元聚合生成三棱柱單元,從而得到半結(jié)構(gòu)化的邊界層網(wǎng)格,并將生成的混合網(wǎng)格應(yīng)用到非定常數(shù)值計(jì)算中[24-25].
本文在前人研究成果的基礎(chǔ)上,基于前沿層推進(jìn)方法,發(fā)展了一套黏性邊界層網(wǎng)格自動(dòng)生成程序,其中的細(xì)節(jié)處理方法,包括前沿多法向的確定以及生長高度的調(diào)節(jié)等,很好地解決了凹凸區(qū)域及角點(diǎn)附近的邊界層網(wǎng)格生成穩(wěn)定性問題,能夠自動(dòng)高效地生成可靠且有效的邊界層網(wǎng)格.同時(shí)發(fā)展了一種三維尺寸調(diào)節(jié)方式,可以為各向同性網(wǎng)格生成器提供均勻尺寸的初始表面網(wǎng)格,進(jìn)而得到高質(zhì)量的遠(yuǎn)場各向同性網(wǎng)格,有利于提高流體計(jì)算解的質(zhì)量.
1 邊界層網(wǎng)格生成流程
本文算法步驟如下:
輸入:計(jì)算區(qū)域物面三角形網(wǎng)格,邊界層首層厚度hf,厚度增長比例hr,層數(shù)nl.
輸出:邊界層網(wǎng)格,及最外層三角形網(wǎng)格前沿.
Step1讀入物面三角形網(wǎng)格數(shù)據(jù),建立網(wǎng)格數(shù)據(jù)結(jié)構(gòu)及拓?fù)潢P(guān)系.
Step2調(diào)整各節(jié)點(diǎn)總生長高度,此時(shí)生長高度為用戶給定總生長高度
Step 2.1提取前沿特征信息,包括特征邊及角點(diǎn)等信息,確定節(jié)點(diǎn)生長線數(shù)量及方向.
Step 2.2根據(jù)特征信息生長對(duì)應(yīng)的單元,采用收縮高度的方式處理單元自交(反轉(zhuǎn))問題,得到各點(diǎn)的合法生長高度.
Step 2.3對(duì)新前沿進(jìn)行全局相交檢測,收縮高度避免全局相交,得到各點(diǎn)新的生長高度.采用拉普拉斯方法進(jìn)行高度光滑處理得到最終的總生長高度.
Step3根據(jù)調(diào)整后的總生長厚度,得到每層生長高度,依次重復(fù)Step2.1—Step2.2,直到達(dá)到邊界層數(shù)nl,對(duì)最外層前沿進(jìn)行全局相交檢測,采用收縮高度的方式處理.
2 前沿節(jié)點(diǎn)生長法向確定
2.1 定義
邊界層網(wǎng)格生成過程中的前沿為表面三角形網(wǎng)格.物面初始三角形網(wǎng)格剖分為初始前沿.前沿上節(jié)點(diǎn) V,其周圍相鄰節(jié)點(diǎn)記為 Pi(i=1,2,···),對(duì)應(yīng)的鄰邊記為 ei(i=1,2,···).
V的鄰邊ei兩側(cè)的三角面片之間的有向二面角記為 θi,θi較大 (大于 240°)的邊定義為特征邊. 鄰邊中存在三條及以上特征邊的節(jié)點(diǎn)稱為角點(diǎn).如圖2標(biāo)出了邊e3及對(duì)應(yīng)的二面角θ3.
2.2 生長法向計(jì)算
計(jì)算每個(gè)節(jié)點(diǎn)周圍的有向二面角,確定其鄰邊中的特征邊,根據(jù)特征邊將節(jié)點(diǎn)周圍的三角面片分組,如圖 2,V點(diǎn)周圍存在三條特征邊 VP1,VP3,VP4,則將周圍的三角面片分為3組.每一組確定一條生長方向ni(i=1,2,3),由該組三角面片的外法向加權(quán)得到,Ni為第i組三角面片數(shù),mj為第 j個(gè)三角片外法向,權(quán)值wj可簡單取為1或者采用文獻(xiàn)[26]中提出的角度權(quán)值
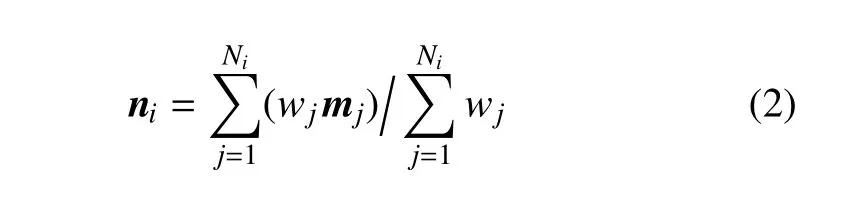
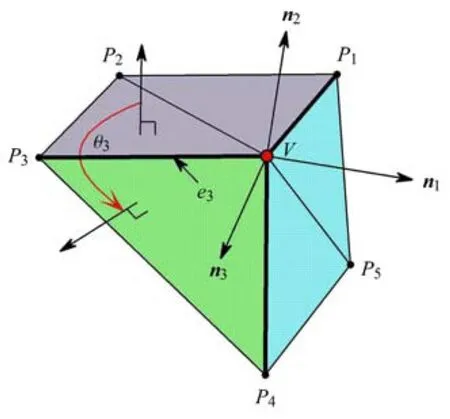
圖2 生長法向確定Fig.2 Calculate growth directions
以上的法向計(jì)算策略能夠很好地滿足推進(jìn)單元正交性及可視化條件,而且三條法向就足夠了.因此本文設(shè)定節(jié)點(diǎn)的生長方向最多有三條.當(dāng)節(jié)點(diǎn)周圍存在三條以上特征邊時(shí),則從中挑出有向二面角最大的三條特征邊作為最后的分組標(biāo)準(zhǔn).
節(jié)點(diǎn)生長法向確定后,周圍三角片在該節(jié)點(diǎn)處有一個(gè)對(duì)應(yīng)的生成法向;特征邊在該點(diǎn)處有一到兩個(gè)生長方向,可由邊兩側(cè)的三角片的對(duì)應(yīng)情況確定.當(dāng)節(jié)點(diǎn)存在三個(gè)生長法向時(shí),該節(jié)點(diǎn)會(huì)單獨(dú)生長出一個(gè)四面體單元.
3 生長高度確定
初始生長高度為用戶給定,即程序的輸入中包含的第一層網(wǎng)格高度hf,生長高度增長比率hr及層數(shù)nl.由于節(jié)點(diǎn)的生長法向不一定都垂直于物面,因此有必要對(duì)初始生長高度進(jìn)行適當(dāng)?shù)恼{(diào)整.按照調(diào)整后的高度信息逐層推進(jìn)生長邊界層,在推進(jìn)過程中,由于邊界形狀的復(fù)雜性,可能出現(xiàn)單元自交及前沿全局相交的問題.因此也需要對(duì)當(dāng)前的生長高度進(jìn)行調(diào)節(jié).
3.1 初始生長高度
在用戶給定初始生長高度等信息作為輸入后,由于上一節(jié)確定的節(jié)點(diǎn)生長方向不一定垂直于節(jié)點(diǎn)周圍所有的三角面片,因此為了盡量保證推進(jìn)前沿與當(dāng)前前沿的距離符合用戶給定的信息,需要對(duì)初始生長高度進(jìn)行適當(dāng)?shù)恼{(diào)整.
對(duì)于二維情況,由于生長法向是節(jié)點(diǎn)外角的N等分線 (N為生長法向數(shù)目),因此只需要考慮法向與物面垂線夾角即可.圖3為二維示意圖,前沿推進(jìn)高度為h,節(jié)點(diǎn)V1有一個(gè)法向,則生長高度為h/sinθ,點(diǎn)V2處θ=90°,所以生長高度為h.
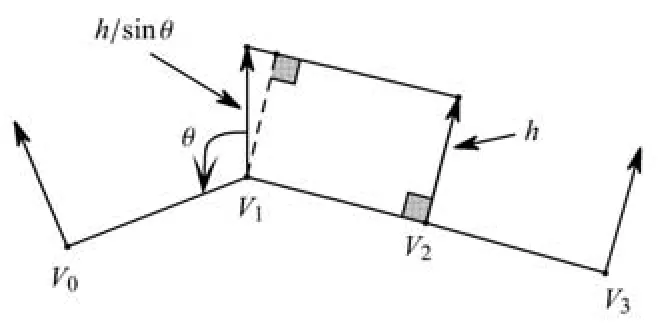
圖3 二維初始高度調(diào)節(jié)Fig.3 2D initial height setting
對(duì)于三維情況,由于采用多生長方向,同時(shí)法向的確定為分組三角面片法向的加權(quán)平均,因此為了保證推進(jìn)前沿與當(dāng)前前沿盡量平行,則需要采用加權(quán)法調(diào)整每個(gè)節(jié)點(diǎn)的初始生長高度.如圖4,節(jié)點(diǎn)V周圍的一個(gè)三角片Ti,其單元法向?yàn)閚T,它對(duì)應(yīng)的分組節(jié)點(diǎn)生長法向?yàn)閚i(節(jié)點(diǎn)V可能有多個(gè)法向,圖4只顯示了對(duì)應(yīng)于Ti的法向ni),則初始高度調(diào)整后為
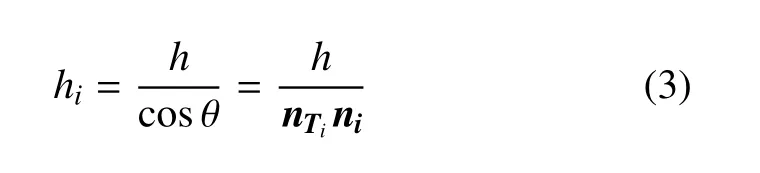
遍歷節(jié)點(diǎn)V周圍所有三角片加權(quán)平均得到節(jié)點(diǎn)V調(diào)整后的初始節(jié)點(diǎn)生長高度hV,記T(V)為節(jié)點(diǎn)V周圍的三角片集合,NT(V)為集合元素個(gè)數(shù),則有
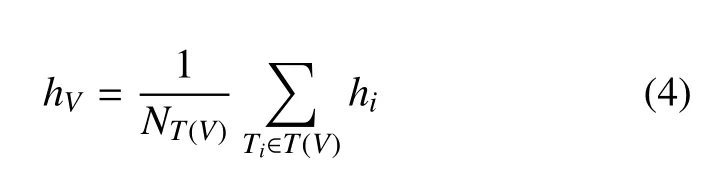
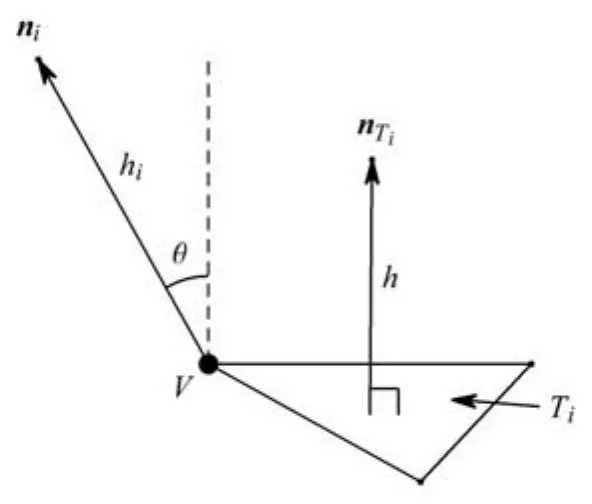
圖4 三維初始高度調(diào)節(jié)Fig.4 3D initial height setting
3.2 自交
自交即單元出現(xiàn)反轉(zhuǎn),如圖5(a)所示.當(dāng)出現(xiàn)自交時(shí),收縮自交單元節(jié)點(diǎn)的生長高度,二維單元?jiǎng)t收縮至交點(diǎn)處,即法向融合,這樣可以避免前沿小尺寸出現(xiàn),同時(shí)也可以減少之后處理自交的頻次.
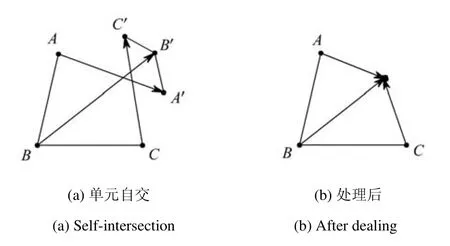
圖5 自交處理二維示意圖Fig.5 Dealing with 2D self-intersection
對(duì)于三維情況,當(dāng)三棱柱單元出現(xiàn)反轉(zhuǎn)時(shí),如圖6,記三角形ABC推進(jìn)到三角形A′B′C′,面積由S變?yōu)镾′,則采取收縮高度的方式處理,收縮因子γ為
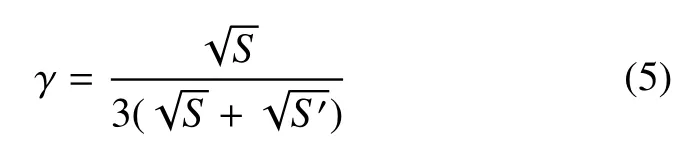
自交處理完以后,需要采用拉普拉斯方法對(duì)前沿各點(diǎn)的生長高度進(jìn)行光滑處理,這樣可以避免三棱柱單元鄰邊突變的情形.
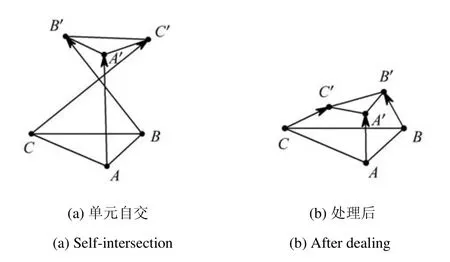
圖6 自交處理三維示意圖Fig.6 Dealing with 3D self-intersection
3.3 全局相交
對(duì)于復(fù)雜的計(jì)算域,前沿層推進(jìn)的過程中,不同物面推進(jìn)的前沿之間可能存在相交的情況,對(duì)于前沿規(guī)模非常大的問題,全局相交檢測是一個(gè)耗時(shí)的過程.為了減少相交檢測的范圍,可以建立八叉樹(二維四叉樹)結(jié)構(gòu)使得全局檢測局部化.盡管八叉樹結(jié)構(gòu)提高了全局相交檢測的效率,但以往的層推進(jìn)方法每一層都需要檢測,使效率下降.為了提高邊界層網(wǎng)格生成的效率,本文的方法先對(duì)全局預(yù)測一個(gè)總生長高度,即先采用總生長高度生長一層邊界層,在單元生長的過程中進(jìn)行自相交處理,得到每個(gè)表面節(jié)點(diǎn)的生長高度,然后進(jìn)行拉普拉斯光滑處理,最后進(jìn)行一次全局相交檢測,采用收縮的方式得到每個(gè)節(jié)點(diǎn)的總生長高度,進(jìn)而得到合適的每層生長高度.采用預(yù)測得到的生長高度進(jìn)行邊界層網(wǎng)格推進(jìn)則可以減少全局相交檢測的次數(shù),提高效率.
圖7所示的是一個(gè)二維全局收縮的示意圖,收縮后的總生長高度能夠較好地避免內(nèi)部邊界層網(wǎng)格前沿的全局相交,因此,在很大程度上能夠避免多次的全局相交檢測及收縮操作.
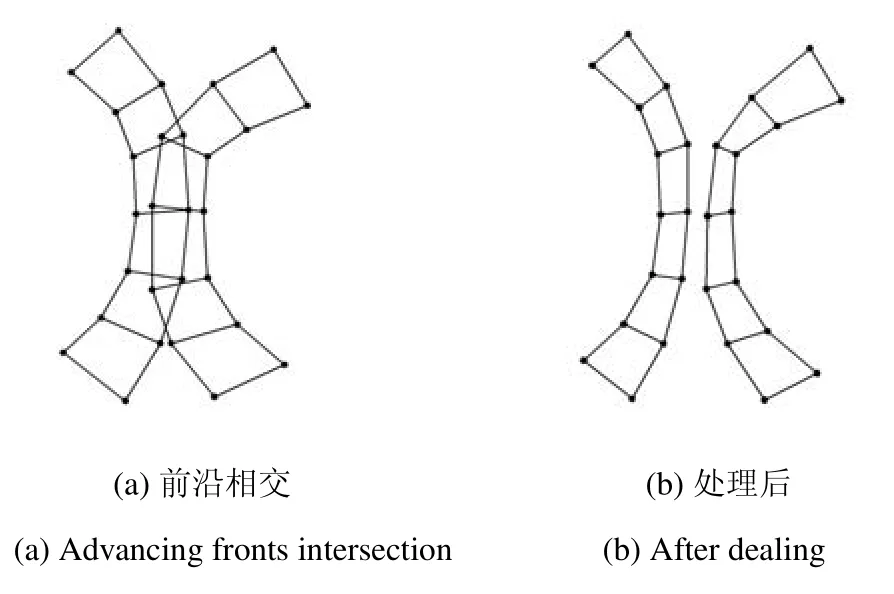
圖7 全局相交處理二維示意圖Fig.7 Dealing with global intersection(2D example)
4 單元生長及前沿尺寸調(diào)節(jié)
4.1 單元生長及細(xì)分
根據(jù)第2節(jié)可知,前沿存在三種特征信息:角點(diǎn),特征邊以及三角片.因此,本文方法的單元生長方式共有如圖8四種情況,粗點(diǎn)及粗線在當(dāng)前前沿上,箭頭表示生長方向:角點(diǎn)生長出一個(gè)四面體單元,三角片生長出一個(gè)三棱柱單元,特征邊則可以生長出一個(gè)三棱柱單元或者一個(gè)退化的三棱柱單元.
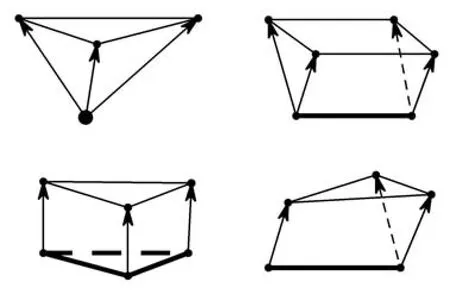
圖8 單元生長示意圖Fig.8 Element growing types
由于大多數(shù)流體求解器局限于純四面體網(wǎng)格[7],為了適應(yīng)大多數(shù)流體求解程序的要求,本文實(shí)現(xiàn)了將得到的邊界層網(wǎng)格轉(zhuǎn)化全四面體網(wǎng)格的過程:連接三棱柱或退化三棱柱的側(cè)面對(duì)角線,將三棱柱細(xì)分為三個(gè)各向異性的四面體單元,如圖9.
為了保持單元之間的相容性,即單元相鄰當(dāng)且僅當(dāng)單元具有共同的節(jié)點(diǎn)、邊或面.然而,不是所有的連接方式都能對(duì)三棱柱單元進(jìn)行有效的剖分,如圖9(a)的S型連接方式則不能對(duì)三棱柱單元進(jìn)行剖分得到三個(gè)四面體單元.因此在連接三棱柱側(cè)邊四邊形對(duì)角線的時(shí)候需要進(jìn)行特殊的處理.
排除以上的S型連接方式,可以得到合法連接的充要條件是存在兩條有公共端點(diǎn)的對(duì)角線.如圖9(b)連接方式將三棱柱剖分為ABCF,ABFE,AEFD三個(gè)四面體.
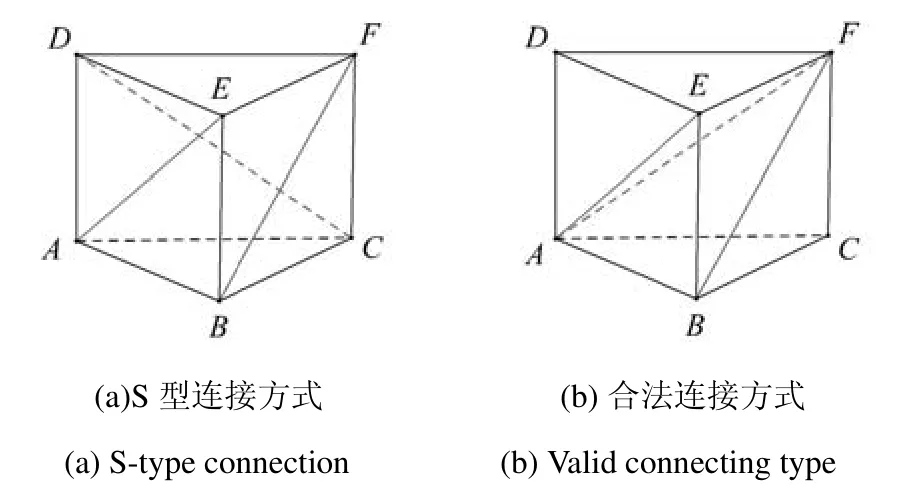
圖9 三棱柱側(cè)面對(duì)角線連接方式Fig.9 Connecting types of diagonals for lateral faces of a prism
因此本文處理連接對(duì)角線的方式為:對(duì)角線統(tǒng)一由編號(hào)小的點(diǎn)連向編號(hào)大的生長點(diǎn),如圖10編號(hào)i1>i0>i2,則對(duì)角線由Pi0和Pi2連向編號(hào)大的點(diǎn)Pi1的生長點(diǎn),Pi2連向Pi0的生長點(diǎn).對(duì)于全部的三棱柱和退化的三棱柱的側(cè)面都進(jìn)行如此連接處理,則可以得到全局相容的四面體網(wǎng)格.
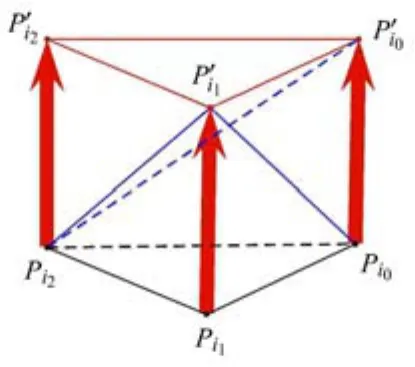
圖10 節(jié)點(diǎn)拓?fù)溥B接關(guān)系示意圖Fig.10 Diagonal choice for prism tetrahedronization
4.2 前沿尺寸調(diào)節(jié)
邊界層網(wǎng)格生成結(jié)束之后,邊界層最外層前沿將作為各向同性網(wǎng)格生成器的表面網(wǎng)格,因此最外層前沿三角網(wǎng)格的質(zhì)量直接關(guān)系到生成的各向同性網(wǎng)格的質(zhì)量.所以,很有必要在生成邊界層網(wǎng)格的同時(shí)進(jìn)行前沿尺寸調(diào)節(jié),為之后的各向同性網(wǎng)格生成提供高質(zhì)量的三角形網(wǎng)格輸入.
在邊界層生長推進(jìn)的過程中,其前沿的尺寸可能不斷發(fā)生變化.二維情況下,在生成邊界層網(wǎng)格時(shí),表面線段在推進(jìn)后的尺寸可能會(huì)變大(變小的情況按自交情況處理),如圖11中的BC推進(jìn)到AD,AD的長度變大,記
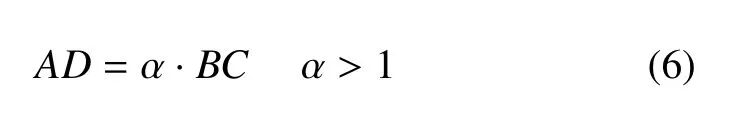
文獻(xiàn)[27]在生成二維混合網(wǎng)格時(shí)對(duì)這種情況進(jìn)行了處理,提出當(dāng)α大于給定值(本文取1.5)時(shí),則取AD中點(diǎn)E,將四邊形單元ABCD細(xì)分為三個(gè)三角形.
本文將其推廣應(yīng)用到三維尺寸控制中.由于三維邊界前沿在推進(jìn)過程中只出現(xiàn)四種情形,角點(diǎn)產(chǎn)生四面體,特征邊和三角面片產(chǎn)生三棱柱,不管哪種情形,其表面只存在兩種形狀:三角形或四邊形.首先標(biāo)記尺寸大的邊,三角形的處理方式為標(biāo)記邊的中點(diǎn)與對(duì)應(yīng)的頂點(diǎn)相連,然后消除標(biāo)記,依次進(jìn)行,直至所有標(biāo)記邊處理結(jié)束;而對(duì)于四邊形,則采用圖11的細(xì)分方式,同時(shí)也加入三角形的操作方式;參照?qǐng)D12,紅色粗線為標(biāo)記的尺寸較大的邊,藍(lán)色線為新加入線.對(duì)應(yīng)于三維中的調(diào)節(jié)操作可參見附錄A,另外有兩種情況需要進(jìn)行一次邊置換操作,如圖13.
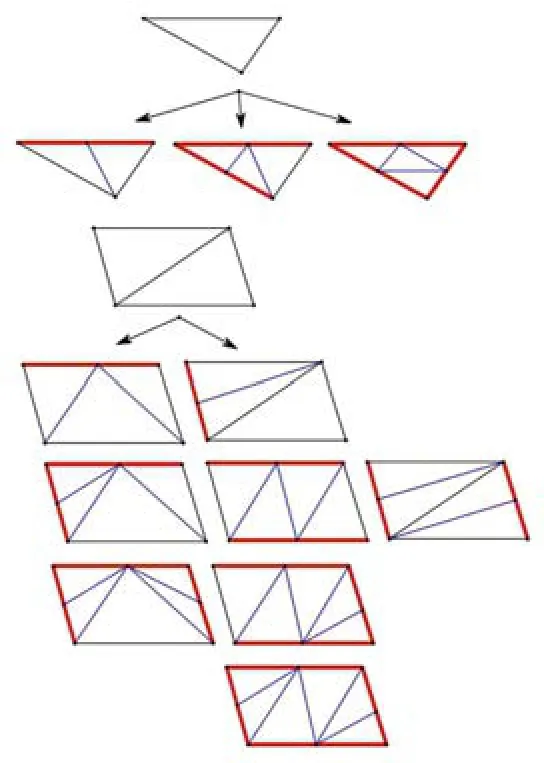
圖12 三角形及四邊形處理方式Fig.12 Subdivision of triangles and quads
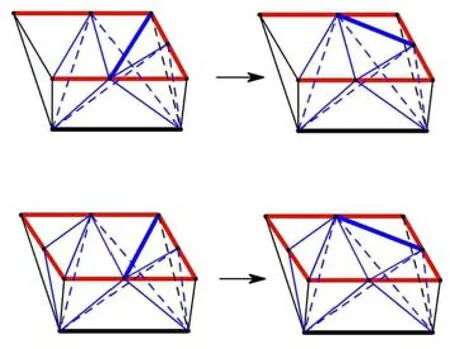
圖13 邊置換操作(藍(lán)色線)Fig.13 Edge swap operation(blue line)
5 邊界層網(wǎng)格生成實(shí)例及數(shù)值驗(yàn)證
程序在輸入物面三角形網(wǎng)格之后,能夠根據(jù)給定的邊界層網(wǎng)格第一層高度、層數(shù)及總高度,自動(dòng)生成邊界層網(wǎng)格.以下實(shí)例的遠(yuǎn)場網(wǎng)格均采用前沿推進(jìn)法[28]生成.同時(shí),為了驗(yàn)證本文生成的混合網(wǎng)格的計(jì)算有效性,采用本文方法生成的混合網(wǎng)格對(duì)二維NACA0012翼型、三維ONERA M6翼型、帶發(fā)動(dòng)機(jī)短艙F6翼身組合體進(jìn)行黏性繞流計(jì)算.
圖14是自交處理和尺寸調(diào)節(jié)結(jié)合的二維實(shí)例圖.從圖中可以看出,調(diào)整生長高度融合生長法向之后,單元自交得到很好的處理(凹角區(qū)域).
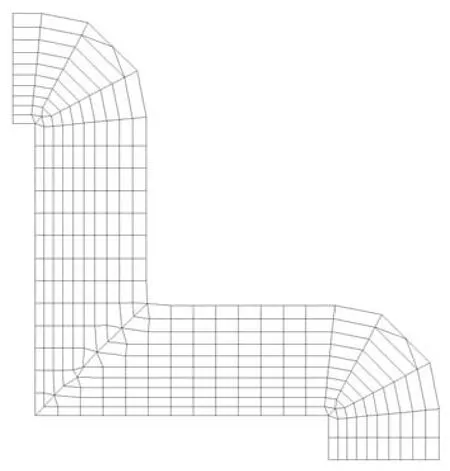
圖14 自交處理和尺寸調(diào)節(jié)二維實(shí)例Fig.14 2D example dealing with self-intersection and size controlling
圖15和圖16為一個(gè)凹槽黏性網(wǎng)格圖,展示了凹角區(qū)域收縮生長高度的效果.
圖15 凹槽黏性網(wǎng)格Fig.15 Viscous mesh example of a cavity
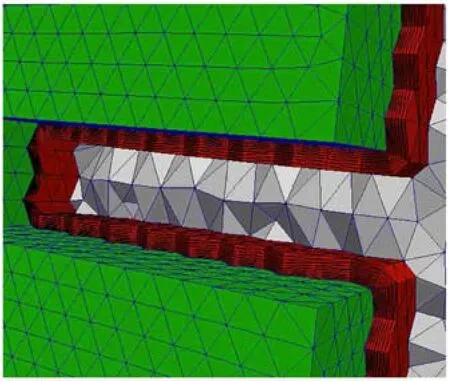
圖16 凹槽黏性網(wǎng)格內(nèi)部放大圖Fig.16 Enlarged inside view of the cavity mesh
5.1 NACA0012翼型
圖17是一個(gè)二維NACA0012翼型混合網(wǎng)格生成實(shí)例,生成20層邊界層網(wǎng)格,含8394個(gè)四邊形,102個(gè)三角形;遠(yuǎn)場包括11302個(gè)三角形.圖18為翼型尾部放大圖.從二維NACA0012實(shí)例可以看出,采用尺寸調(diào)節(jié)后,最外層前沿線段長度比較均勻,因此邊界層網(wǎng)格與遠(yuǎn)場網(wǎng)格銜接較好.

圖17 NACA0012二維混合網(wǎng)格Fig.17 2D hybrid mesh for NACA0012
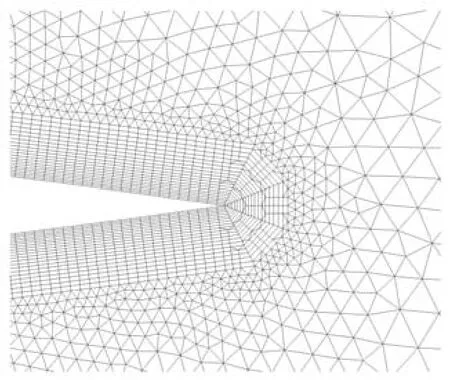
圖18 NACA0012二維混合網(wǎng)格尾部放大圖Fig.18 Enlarged view of the 2D hybrid mesh of NACA0012
圖19是一個(gè)三維NACA0012混合網(wǎng)格生成實(shí)例,生成10層邊界層網(wǎng)格,包括36819個(gè)四面體;遠(yuǎn)場包含22787個(gè)四面體.圖20為內(nèi)部視圖,可以看出多生長方向提高了邊界層網(wǎng)格的正交性.
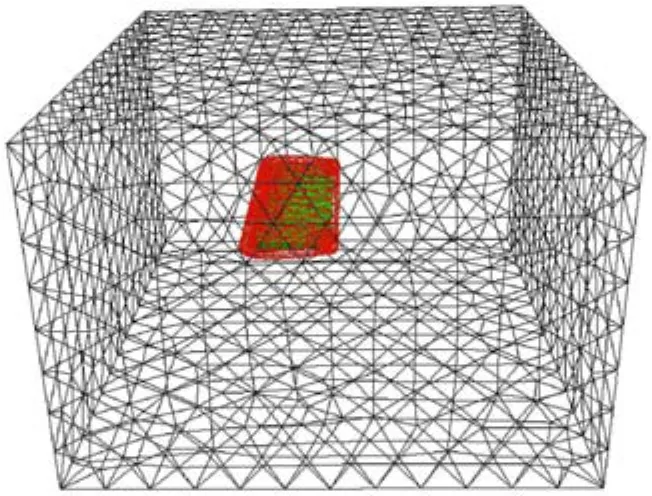
圖19 NACA0012三維網(wǎng)格Fig.19 3D hybrid mesh of NACA0012
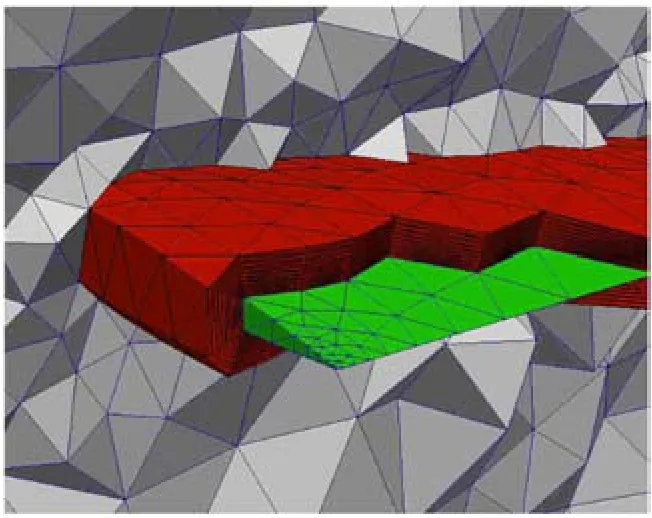
圖20 NACA0012三維網(wǎng)格內(nèi)部視圖Fig.20 Inside view of the 3D hybrid mesh of NACA0012
二維NACA0012翼型繞流的入口邊界馬赫數(shù)為0.8,攻角為0°,采用Spalart-Allmaras湍流模型,得到的壓力分布云圖如圖21所示,其上表面壁面附近的速度矢量圖如圖22所示,從結(jié)果可以看出本文采用的混合網(wǎng)格能夠捕捉壁面附近及流場內(nèi)部的信息,網(wǎng)格是有效的.

圖21 二維NACA0012壓力分布云圖Fig.21 Pressure contours of NACA0012 wing
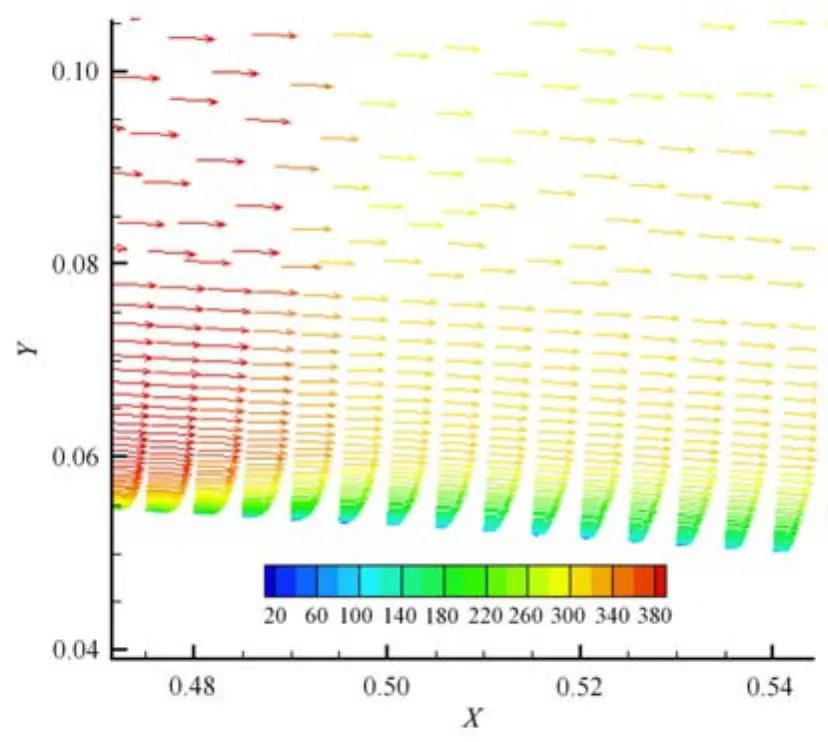
圖22 機(jī)翼上表面附近速度矢量圖Fig.22 Velocity vectors near upper wing surface
5.2 三維ONERA M6翼型
采用本文方法生成M6的黏性混合網(wǎng)格如圖23所示,圖24為內(nèi)部視圖.

圖24 ONERA M6混合網(wǎng)格內(nèi)部視圖Fig.24 Inside view of hybrid mesh of M6 wing
為了與現(xiàn)有實(shí)驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比,三維M6翼型繞流采用標(biāo)準(zhǔn)實(shí)驗(yàn)工況,Ma=0.8395,攻角為3.06°,采用k-ω湍流模型,機(jī)翼不同站位上的壓力系數(shù)分布計(jì)算值與實(shí)驗(yàn)數(shù)據(jù)[29]對(duì)比如圖25~圖29.選取的站位y/b分別為0.2,0.44,0.65,0.8,0.9.
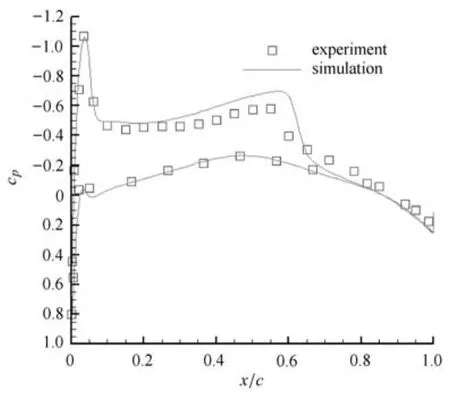
圖25 y/b=0.2壓力系數(shù)分布Fig.25 Pressure coeffients on the wing surface at y/b=0.2
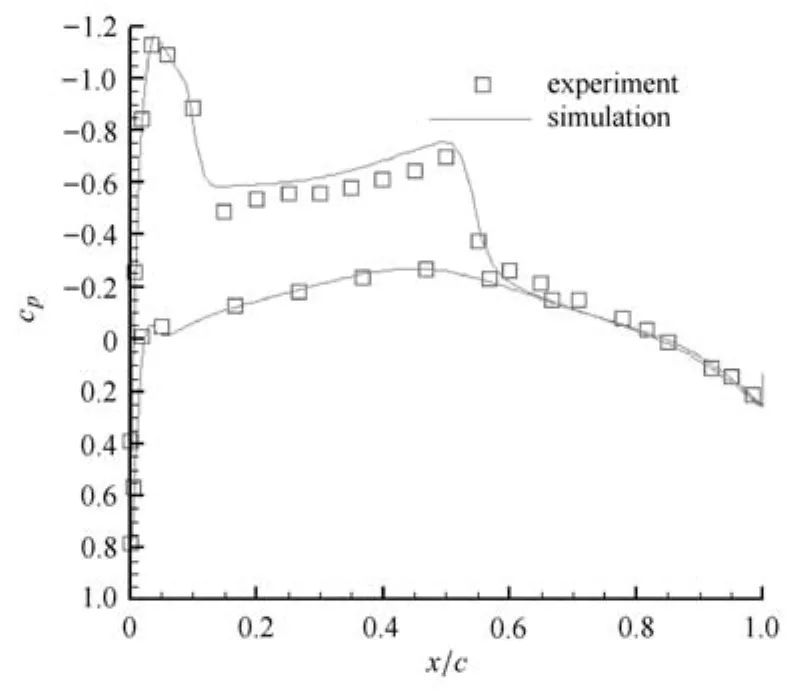
圖26 y/b=0.44壓力系數(shù)分布Fig.26 Pressure coeffients on the wing surface at y/b=0.44
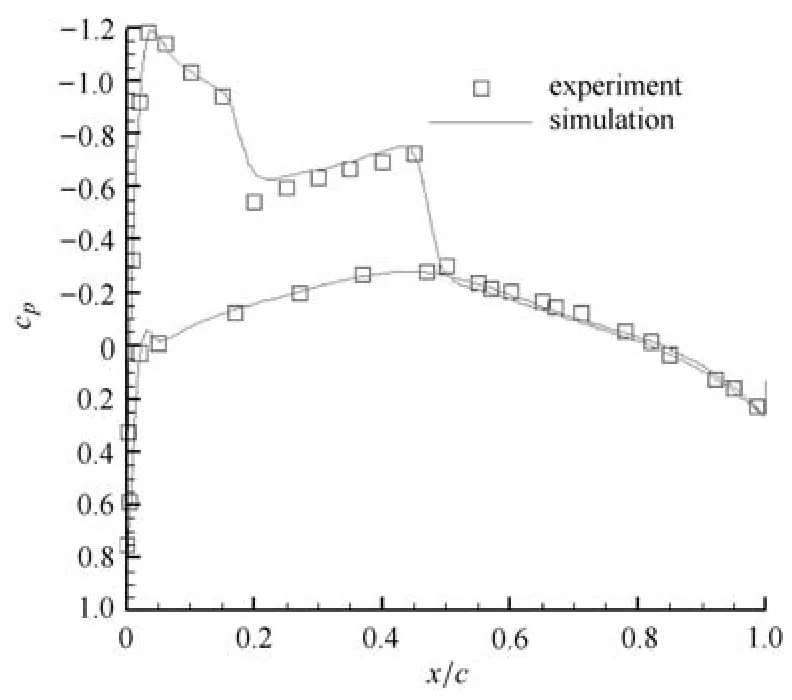
圖27 y/b=0.65壓力系數(shù)分布Fig.27 Pressure coeffients on the wing surface at y/b=0.65

圖28 y/b=0.8壓力系數(shù)分布Fig.28 Pressure coeffients on the wing surface at y/b=0.8
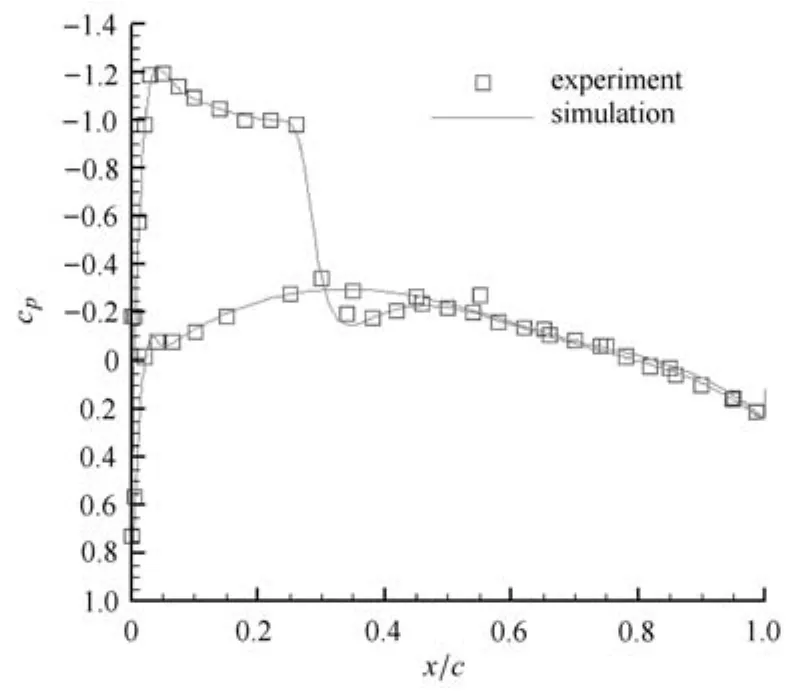
圖29 y/b=0.9壓力系數(shù)分布Fig.29 Pressure coeffients on the wing surface at y/b=0.9
從圖中對(duì)比可以看出,壓力系數(shù)分布總體上吻合得較好,各站位上的激波位置捕捉較為理想.總之,從對(duì)比結(jié)果可以看出本文生成的黏性混合網(wǎng)格能夠有效應(yīng)用到黏性繞流計(jì)算中.
5.3 帶發(fā)動(dòng)機(jī)短艙的F6翼身組合體
采用本文方法對(duì)F6翼身組合體進(jìn)行黏性混合網(wǎng)格生成,圖30為內(nèi)部網(wǎng)格剖分圖.

圖30 DLR-F6混和網(wǎng)格內(nèi)部視圖Fig.30 Inside view of hybrid mesh of DLR-F6
計(jì)算中,為了與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比,采用Ma=0.75,Re=3×106,α=1.738的計(jì)算條件,文獻(xiàn)[30]表明計(jì)算結(jié)果與湍流模型的選取有關(guān),本文的湍流模型采用k-ω模型.將得到的機(jī)翼不同站位上的壓力系數(shù)與實(shí)驗(yàn)值[31]進(jìn)行對(duì)比.圖31~圖38展示了計(jì)算結(jié)果與所有8個(gè)實(shí)驗(yàn)站位上的對(duì)比圖.從圖中可以看出,計(jì)算結(jié)果與實(shí)驗(yàn)得到的物面壓力系數(shù)分布較為符合,同時(shí)激波位置的捕捉也較為準(zhǔn)確,因此本文生成的混合網(wǎng)格運(yùn)用到F6翼身組合體的繞流計(jì)算是有效的.
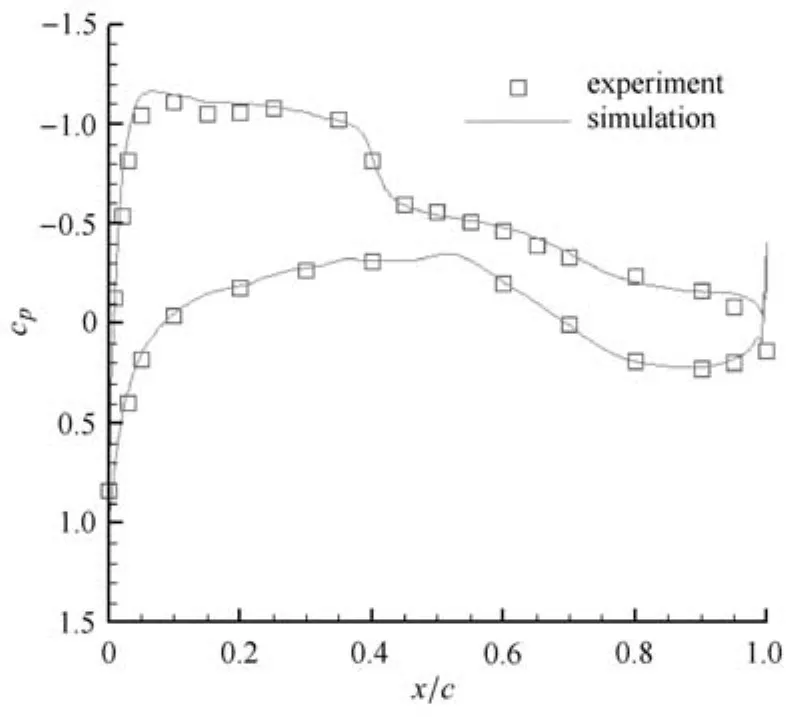
圖31 y/b=0.15壓力系數(shù)分布Fig.31 Pressure coeffients on the wing surface at y/b=0.15
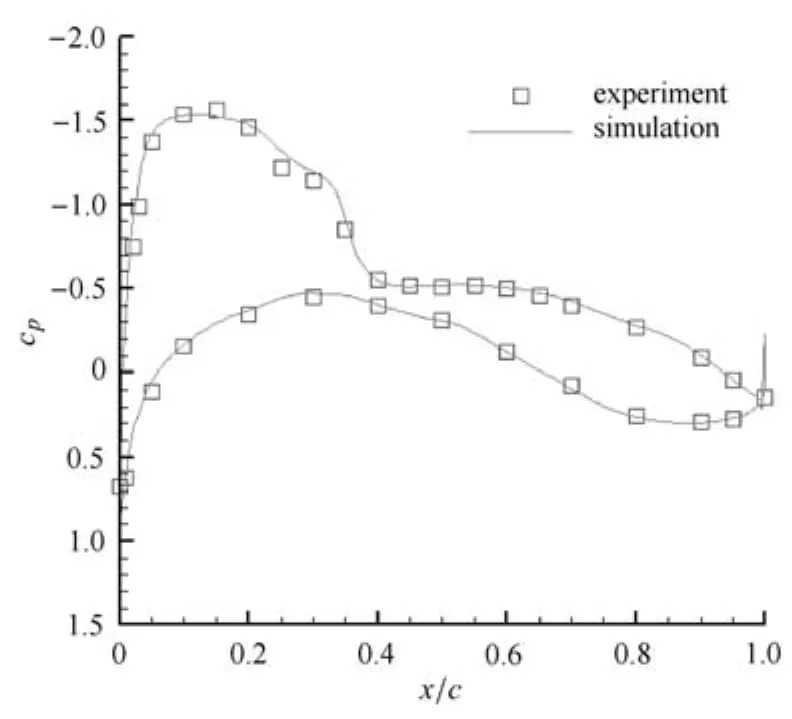
圖32 y/b=0.239壓力系數(shù)分布Fig.32 Pressure coeffients on the wing surface at y/b=0.239
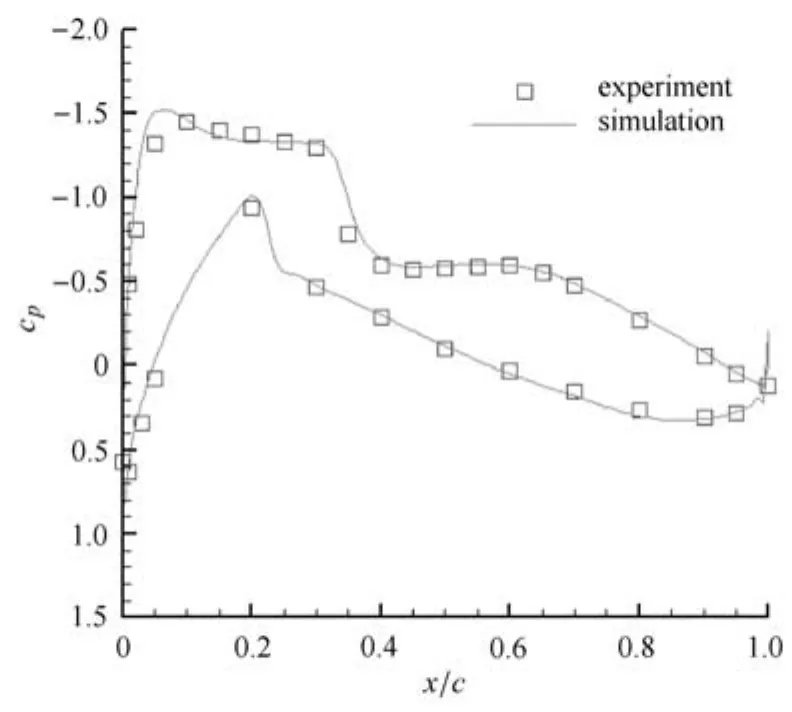
圖33 y/b=0.331壓力系數(shù)分布Fig.33 Pressure coeffients on the wing surface at y/b=0.331
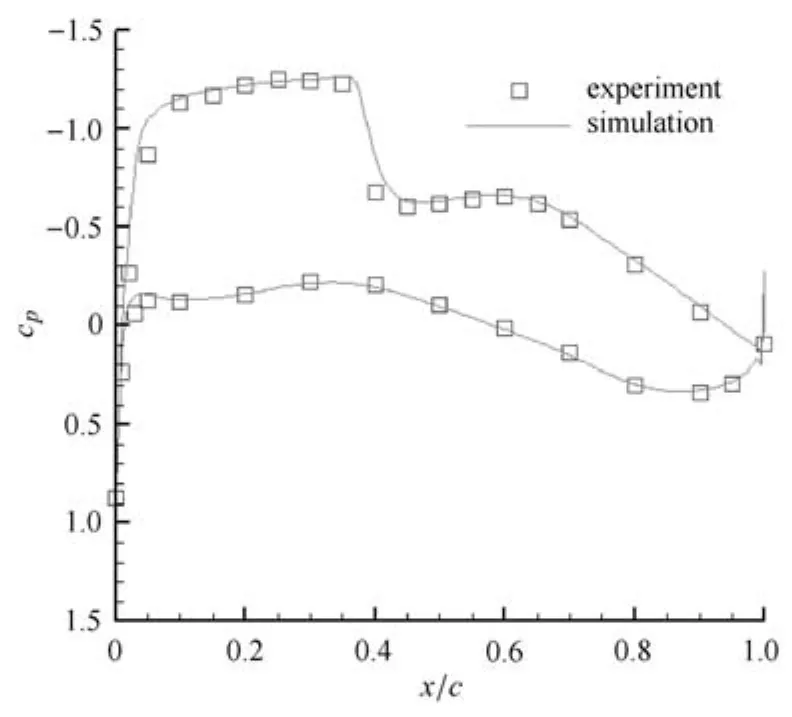
圖34 y/b=0.377壓力系數(shù)分布Fig.34 Pressure coeffients on the wing surface at y/b=0.377
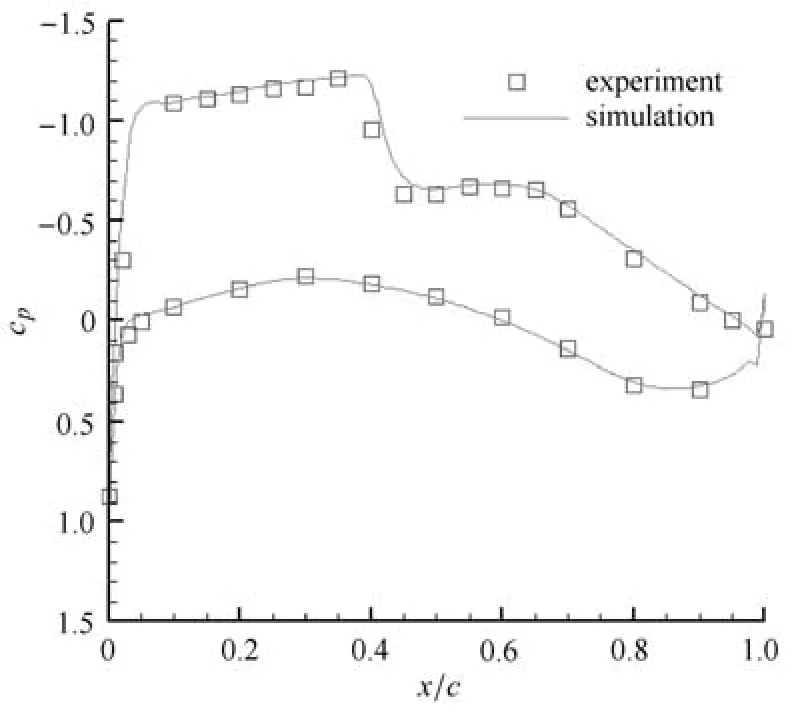
圖35 y/b=0.411壓力系數(shù)分布Fig.35 Pressure coeffients on the wing surface at y/b=0.411
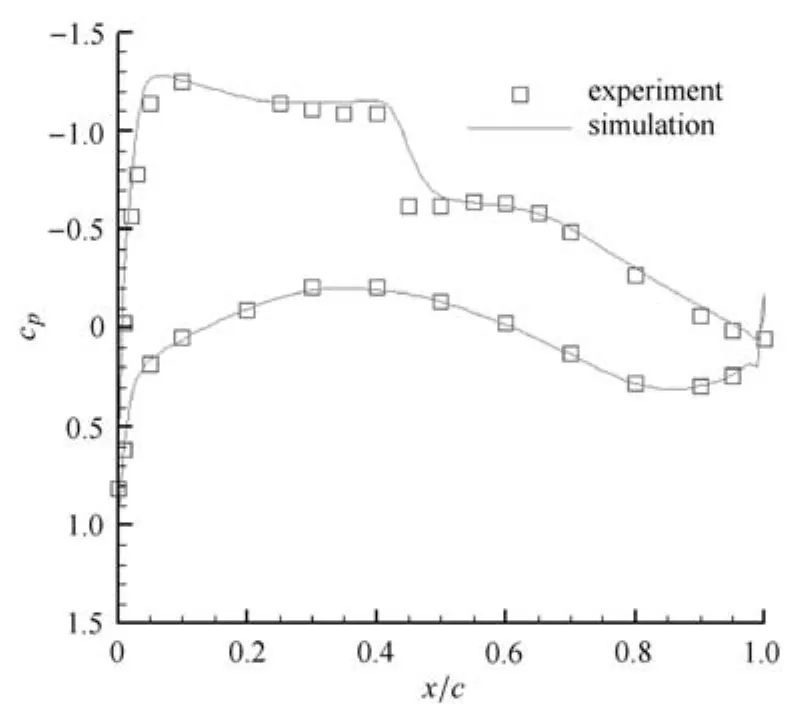
圖36 y/b=0.514壓力系數(shù)分布Fig.36 Pressure coeffients on the wing surface at y/b=0.514
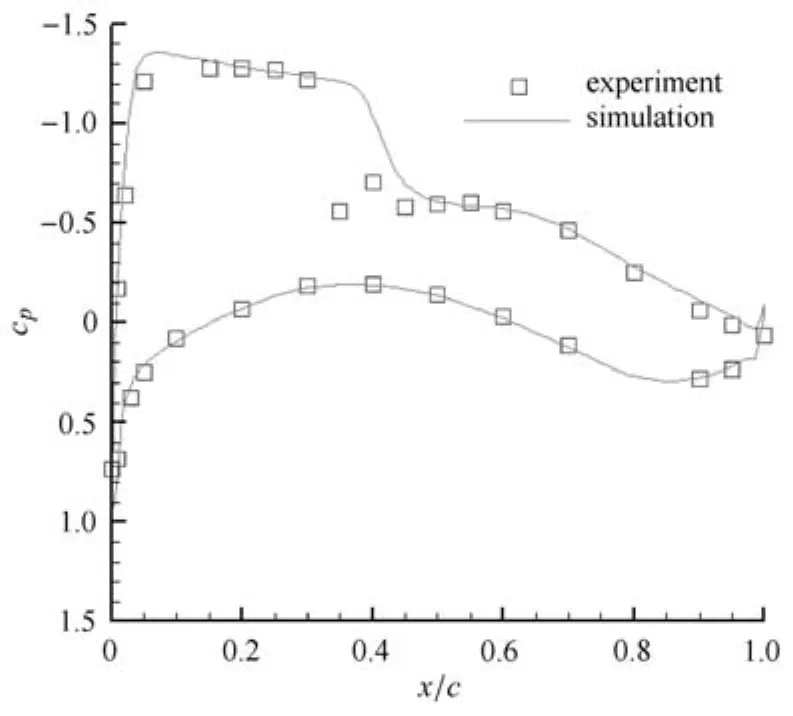
圖37 y/b=0.638壓力系數(shù)分布Fig.37 Pressure coeffients on the wing surface at y/b=0.638
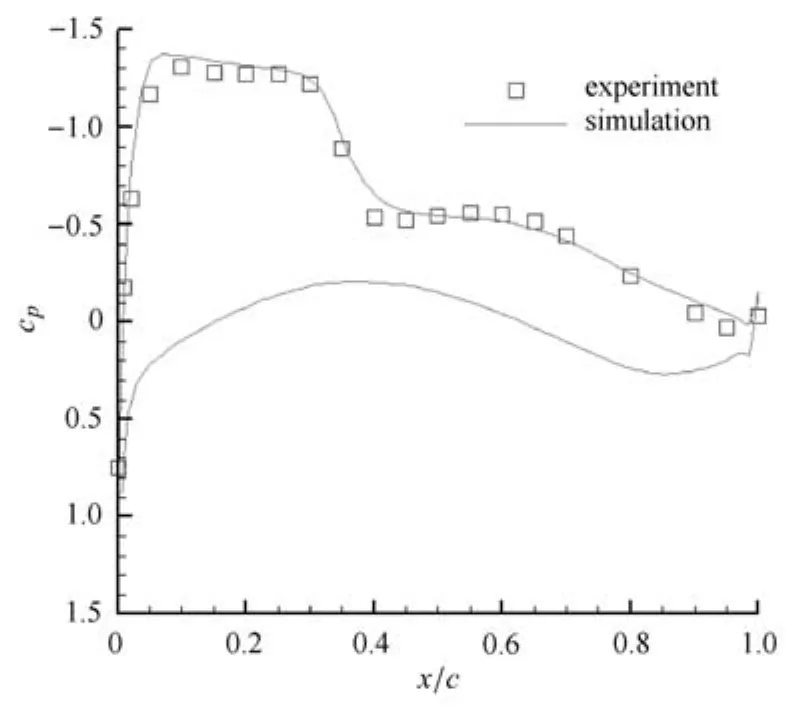
圖38 y/b=0.847壓力系數(shù)分布Fig.38 Pressure coeffients on the wing surface at y/b=0.847
6 結(jié)論
本文提出的黏性邊界層網(wǎng)格自動(dòng)生成策略可以很好地解決物面凹凸區(qū)域及角點(diǎn)處邊界層網(wǎng)格的生長問題,避免產(chǎn)生非法單元,同時(shí)減少全局相交檢測的次數(shù),提高了網(wǎng)格生成的效率;另外還發(fā)展了一種三維尺寸調(diào)節(jié)方法,保證了邊界層網(wǎng)格最外層三角形網(wǎng)格的尺寸統(tǒng)一,有利于生成高質(zhì)量的各向同性遠(yuǎn)場網(wǎng)格.最后將本文生成的二維及三維的黏性混合網(wǎng)格應(yīng)用到高雷諾數(shù)黏性繞流計(jì)算中,得到的計(jì)算結(jié)果表明本方法生成的黏性混合網(wǎng)格能夠滿足實(shí)際計(jì)算的要求,得到合理的計(jì)算結(jié)果.結(jié)合網(wǎng)格變形方法,如彈簧類方法,代數(shù)插值類方法[32]等,本文提出的混合網(wǎng)格生成策略也將很快應(yīng)用到非定常流場計(jì)算[3334]中.
本文在處理自交或全局相交時(shí)只采用收縮因子的形式,在容易產(chǎn)生自交的凹角區(qū)域,其法向推進(jìn)距離小于其他區(qū)域,前沿尺寸也相應(yīng)減小,如圖39所示為凹角區(qū)域收縮效果,在該區(qū)域的未推進(jìn)空間過小,生成各向同性網(wǎng)格會(huì)有一定困難.目前的處理方式是增加該區(qū)域表面網(wǎng)格的密度,減小表面網(wǎng)格尺寸,即生成的初始表面網(wǎng)格在凹凸脊及角點(diǎn)區(qū)域的單元會(huì)加密.同樣,在一些狹縫區(qū)域,兩側(cè)壁面同時(shí)推進(jìn)的情況下,由于空間狹小,會(huì)造成未推進(jìn)區(qū)域過小,給各向同性網(wǎng)格生成造成困難.本文實(shí)例中尚未涉及此種特別狹窄的區(qū)域,全局的前沿合并策略是解決這類情況的一種好的方式,將在今后的工作中進(jìn)一步考慮和完善.

圖39 凹角網(wǎng)格收縮效果Fig.39 Mesh shrinking at concave ridges
另外,本文的程序?qū)⒈砻婢W(wǎng)格直接作為輸入,計(jì)算域邊界的表面三角剖分對(duì)于邊界層網(wǎng)格的順利進(jìn)行具有重要意義[6,35],因此,在生成邊界層網(wǎng)格之前,如何獲得適用于邊界層推進(jìn)的高質(zhì)量的表面網(wǎng)格值得進(jìn)一步研究.
1 Sahni O,Jansen KE,Shephard MS,et al.Adaptive boundary layer meshing for viscous fl ow simulations.Engineering with Computers,2008,24(3):267-285
2 Pirzadeh S.Unstructured viscous grid generation by the advancinglayers method.AIAA Journal,1994,32(8):1735-1737
3 Kallinderis Y,Ward S.Prismatic grid generation for threedimensional complex geometries.AIAA Journal,1993,31(10):1850-1856
4 Lohner R.Matching semi-structured and unstructured grids for Navier–Stokes calculations.AIAA Paper 1993-3348,Orlando,FL,U.S.A.1993
5 Aubry R,L¨ohner R.On the‘most normal’normal.Communications in Numerical Methods in Engineering,2008,24(12):1641-1652
6 Aubry R,Dey S,Mestreau E,et al.An entropy satisfying boundary layer surface mesh generation.SIAM Journal on Scienti fi c Computing,2015,37(4):A1957-A1974
7 Aubry R,Dey S,Karamete K,et al.Smooth anisotropic sources with application to three-dimensional surface mesh generation.Engineering with Computers,2016,32(2):313-330
8 Dey S,Aubry R,Karamete B,et al.Capstone:A geometry-centric platform to enable physics-based simulation and design of systems.Computing in Science&Engineering,2016,18(1):32-39
9 Connell SD,Braaten ME.Semistructured mesh generation for threedimensional Navier-Stokes calculations.AIAA Journal,1995,33(6):1017-1024
10 Garimella RV,Shephard MS.Boundary layer mesh generation for viscous fl ow simulations. International Journal for Numerical Methods in Engineering,2000,49(1):193-218
11 Athanasiadis AN,Deconinck H.Object-oriented three-dimensional hybrid grid generation.International Journal for Numerical Methods in Engineering,2003,58(2):301-318
12 Athanasiadis AN,Deconinck H.A folding/unfolding algorithm for the construction of semi-structured layers in hybrid grid generation.Computer Methods in Applied Mechanics and Engineering,2005,194(48):5051-5067
13 Sharov D,Luo H,Baum JD,et al.Unstructured Navier-Stokes grid generation at corners and ridges.International Journal for Numerical Methods in Fluids,2003,43(6-7):717-728
14 王剛,葉正寅,陳迎春.三維非結(jié)構(gòu)黏性網(wǎng)格生成方法.計(jì)算物理,2001,18(5):402-406(Wang Gang,Ye Zhengyin,Chen Yingchun.Generation of three-dimensional unstructured viscous grids.Chinese Journal of Computational Physics,2001,18(5):402-406(in Chinese))
15 王剛,葉正寅.三維非結(jié)構(gòu)混合網(wǎng)格生成與N-S方程求解.航空學(xué)報(bào),2003,24(5):385-390(Wang Gang,Ye Zhengyin.Generation of three dimensional mixed and unstructured grids and its application in solving Navier-Stokes equations.Acta Aeronautica et Astronautica Sinica,2003,24(5):385-390(in Chinese))
16 陳建軍,曹建,徐彥等.適應(yīng)復(fù)雜外形的三維黏性混合網(wǎng)格生成算法.計(jì)算力學(xué)學(xué)報(bào),2014,31(3):363-370(Chen Jianjun,Cao Jian,Xu Yan,et al.Hybrid mesh generation algorithm for viscous computations of complex aerodynamics con fi gurations.Chinese Journal of Computational Mechanics,2014,31(3):363-370(in Chinese))
17 Dyedov V,Einstein DR,Jiao X,et al.Variational generation of prismatic boundary-layer meshes for biomedical computing.International Journal for Numerical Methods in Engineering,2009,79(8):907-945
18 Jiao X.Face o ff setting:A uni fi ed approach for explicit moving interfaces.Journal of Computational Physics,2007,220(2):612-625
19 Ito Y,Nakahashi K.Improvements in the reliability and quality of unstructured hybrid mesh generation.International Journal for Numerical Methods in Fluids,2004,45(1):79-108
20 Alauzet F,Marcum D.A closed advancing-layer method with connectivity optimization-based mesh movement for viscous mesh generation.Engineering with Computers,2015,31(3):545-560
21 Zhang L,Zhao Z,Chang X,et al.A 3D hybrid grid generation technique and a multigrid/parallel algorithm based on anisotropic agglomeration approach.Chinese Journal of Aeronautics,2013,26(1):47-62
22 Zhong Z,Zhang L P,Xin H E.Hybrid grid generation technique for complex geometries based on agglomeration of anisotropic tetrahedrons.Acta Aerodynamica Sinica,2013,31(1):34-39
23 張來平,張涵信.復(fù)雜無粘流場數(shù)值模擬的矩形/三角形混合網(wǎng)格技術(shù).力學(xué)學(xué)報(bào),1998,30(1):104-108(Zhang Laiping,Zhang Hanxin.A Cartesian/triangular hybrid grid solver for complex inviscid fl ow fi elds.Acta Mechanica Sinica,1998,30(1):104-108(in Chinese))
24 張來平,王志堅(jiān),張涵信.動(dòng)態(tài)混合網(wǎng)格生成及隱式非定常計(jì)算方法.力學(xué)學(xué)報(bào),2004,36(6):664-672(Zhang Laiping,Wang Zhijian,Zhang Hanxin.Hybrid moving grid generation and implicit algorithm for unsteady fl ows.Acta Mechanica Sinica,2004,36(6):664-672(in Chinese))
25 張來平,常興華,段旭鵬,等.基于動(dòng)態(tài)混合網(wǎng)格的不可壓非定常流計(jì)算方法.力學(xué)學(xué)報(bào),2007,39(5):577-586(Zhang Laiping,Chang Xinghua,Duan Xupeng,et al.Implicit algorithm based on dynamic hybrid mesh for incompressible unsteady fl ows.Acta Mechanica Sinica,2007,39(5):577-586(in Chinese))
26 Th¨urrner G,W¨uthrich C A.Computing vertex normals from polygonal facets.Journal of Graphics Tools,1998,3(1):43-46
27 Dussin D,Fossati M,Guardone A,et al.Hybrid grid generation for two-dimensional high-Reynolds fl ows.Computers&Fluids,2009,38(10):1863-1875
28 Geuzaine C,Remacle JF.Gmsh:A 3-D fi nite element mesh generator with built-in pre-and post-processing facilities.International JournalforNumericalMethodsinEngineering,2009,79(11):1309-1331
29 Schmitt V,Charpin F.Pressure distributions on the ONERA-M6-Wing at transonic Mach numbers,experimental data base for computer program assessment.Report of the Fluid Dynamics Panel Working Group 04,AGARD AR-138,1979.
30 石磊,楊云軍,周偉江等.兩種湍流模型在高速旋轉(zhuǎn)翼身組合彈箭中的對(duì)比研究.力學(xué)學(xué)報(bào),2017,49(1):84-92(Shi Lei,Yang Yunjun,Zhou Weijiang.A comparative study of two turbulence models for Magnus e ff ect in spinning projectile.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):84-92(in Chinese))
31 La fl in KR,Brodersen O.Summary of data from the Second AIAA CFD Drag Prediction Workshop.AIAA2004-0555,2004
32 劉中玉,張明鋒,聶雪媛等.一種基于徑向基函數(shù)的兩步法網(wǎng)格變形策略.力學(xué)學(xué)報(bào),2015,47(3):534-538(Liu Zhongyu,Zhang Mingfeng,Wei Xueyuan,et al.A two-step mesh deformation strategy based on radial basis function.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3):534-538(in Chinese))
33 常興華,馬戎,張來平等.基于計(jì)算流體力學(xué)的“虛擬飛行”技術(shù)及初步應(yīng)用.力學(xué)學(xué)報(bào),2015,47(4):596-604(Chang Xinghua,Ma Rong,Zhang Laiping,et al.Study on CFD-based numerical virtual fl ight technology and preliminary application.Chinese Journal of Theoretical and Applied Mechanics,2015,47(4):596-604(in Chinese))
34 童福林,李新亮,唐志共.激波與轉(zhuǎn)捩邊界層干擾非定常特性數(shù)值分析.力學(xué)學(xué)報(bào),2017,49(1):93-104(Tong Fulin,Li Xinliang,Tang Zhigong.Numerical analysis of unsteady motion in shock wave/transitional boundary layer interaction.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):93-104(in Chinese))
35 Aubry R.Ensuring a smooth transition from semi-structured surface boundary layer mesh to fully unstructured anisotropic surface mesh//53rd AIAA Aerospace Sciences Meeting and Exhibit,AIAA,Reston,VA,2015,AIAA-2015-1507
AUTOMATIC VISCOUS BOUNDARY LAYER MESH GENERATION1)
Gan Yangke Liu Jianfei2)
(Department of Mechanics and Engineering Science,College of Engineering,Peking University,Beijing 100871,China)
High Reynolds number fl uid fl ows have boundary layers at the wall.To automatically generate robust and valid boundary layer mesh for the simulations is still the bottleneck problem of computational fl uid dynamics.Prisms/Tetrahedra hybrid mesh leads to signi fi cant savings in mesh size and solution costs.However,it’s still difficult to generate prismatic elements of high quality within boundary layers of complex models.Previous advancing layers techniques sometimes lead to invalid meshes and poor quality elements at concave/convex ridges and sharp corners.To improve these situations,we present a strategy for automatically generating viscous boundary layer mesh.In this method,multiple growth directions at ridges and corners are well de fi ned by the dihedral angles around the vertices and the growth heights are adjusted appropriately.Therefore,boundary layer mesh grows well at sharp corners,convex and concave ridges of the domain.We also decrease the number of global intersection checks by prede fi ning the total growth heights before generating elements through one global check,which improves the efficiency of mesh generation.At the same time,we develop a 3D strategy of mesh size control to get a size uniform triangular mesh of the outer boundary of the boundary layer mesh,which is bene fi cial to generate far- fi eld isotropic mesh of high quality.Finally,mesh examples and the viscous fl ow simulations including 2D and 3D are presented.In 3D,the hybrid mesh over the standard ONERA M6 and DLR-F6 con fi gurations are generated with the present method.The numerical results agree very well with experiment data which indicates that the hybrid viscous meshes generated by the proposed method are e ff ective and efficient.
boundary layer mesh,growth normal,feature edge,intersection,size control
O242.21
A
10.6052/0459-1879-17-154
2017–05–04收稿,2017–07–05 錄用,2017–07–07 網(wǎng)絡(luò)版發(fā)表.
1)國家自然科學(xué)基金(11172005)和國家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃(2010CB832701)資助項(xiàng)目.
2)劉劍飛,副教授,主要研究方向:網(wǎng)格生成,計(jì)算幾何,計(jì)算機(jī)圖形學(xué).E-mail:liujianfei@pku.edu.cn
甘洋科,劉劍飛.黏性邊界層網(wǎng)格自動(dòng)生成.力學(xué)學(xué)報(bào),2017,49(5):1029-1041
Gan Yangke,Liu Jianfei.Automatic viscous boundary layer mesh generation.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1029-1041
附錄A三維邊界層網(wǎng)格生成中單元尺寸調(diào)節(jié)操作
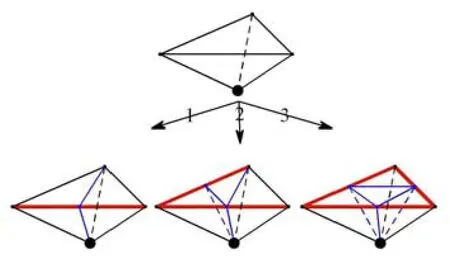
角點(diǎn)生成的四面體Tetraheron generated from one corner
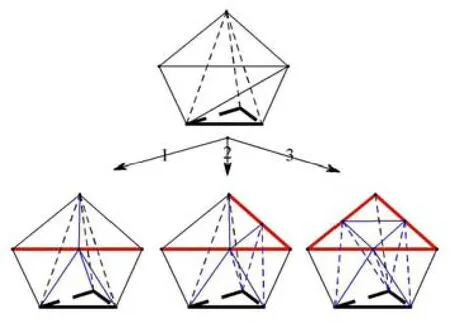
三角片生成的三棱柱Prism generated from one triangle
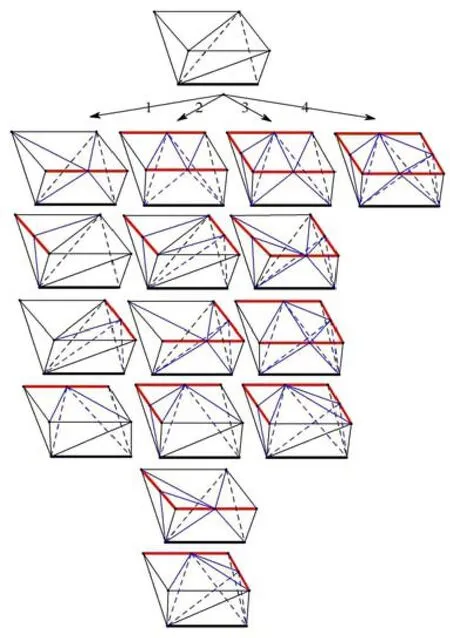
特征邊生成的三棱柱Prism generated from one feature edge

