一類具有飽和發生率的SEIR模型的穩定性

楊彩虹，胡志興

(北京科技大學 數理學院，北京 100083)

?

一類具有飽和發生率的SEIR模型的穩定性

楊彩虹，胡志興

(北京科技大學 數理學院，北京 100083)

討論了一類具有垂直傳染與飽和發生率的SEIR模型的穩定性，考慮了接種免疫對傳染病傳播的影響。通過計算得到模型的基本再生數R0，證明了當R0≤1時，無病平衡點是局部漸近穩定和全局漸近穩定的。利用Hurwitz判據和第二加性復合矩陣證明了當R0>1時，地方病平衡點是局部漸近穩定的，且在一定條件下是全局漸近穩定的。

垂直傳染；飽和發生率；SEIR；穩定性

0　引言

傳染病嚴重威脅人類健康，所以對傳染病模型的研究越來越得到人們的重視，而且近20年來的研究也取得了顯著成果。比較簡單的傳染病模型有易感者-患病者(susceptible-infectious，SI)模型、易感者-患病者-康復者(susceptible-infectious-recovered，SIR)模型和易感者-潛伏者-患病者-康復者(susceptible-exposed-infectious-recovered，SEIR)模型等倉室模型。 文獻[1-2]對具有飽和感染率、飽和治愈率以及垂直感染的SIR傳染病模型進行了研究,這類模型將人口種群分為易感者S、患病者I和康復者R，簡稱SIR模型，研究發現：系統會出現后向分支和hopf分支，并分析了此類傳染病的傳播過程和預防治療方向。然而現實生活中有些傳染病是具有潛伏期的，一般將攜帶病毒但沒有發病的人群記為潛伏者E，對這類傳染病可建立SEIR倉室模型。文獻[3]分別對SIR模型和SEIR模型進行了討論，發現雖然SEIR模型比SIR模型復雜，但研究方法和結果有許多相似之處，而且當具有線性治愈率時，系統僅存在無病平衡點和一個地方病平衡點，當然也存在眾多差異。文獻[4-5]針對SEIR模型進行了詳細研究，本文在其基礎上建立了更加簡單而且適用范圍更廣的SEIR模型。

1　模型的建立

考慮到接觸傳播、垂直傳播、預防接種和有效治療這幾個因素的綜合影響，建立模型并做如下假設和說明:

(Ⅰ)S、E、I和R分別為易感者、潛伏者、患病者和康復者。

(Ⅱ)人口總數記為N，N=S+E+I+R。

(Ⅲ)b為S、E和R的總出生率和死亡率；δ為I的出生率和死亡率；m′為對易感者、潛伏者和康復者的新生兒的預防接種比例(m+m′=1)；q為垂直感染率(p+q=1)；ω為潛伏者轉變成患病者的概率；ε為潛伏者的恢復率；γ為患病者的恢復率。

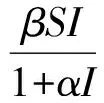
模型為：

(1)

2　平衡點

(2)

將系統(2)的3個方程相加得：

可以證得：

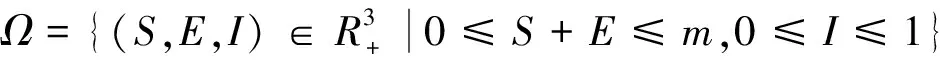
(3)

顯然Ω為系統(2)的正向不變集,下面僅在Ω內討論系統(2)。

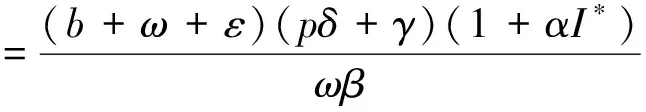
(4)

(5)

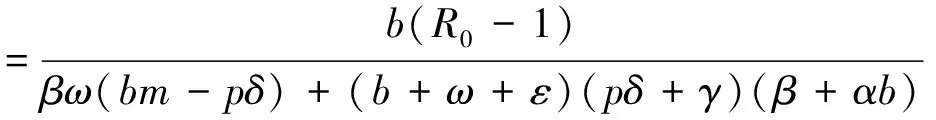
(6)

3　無病平衡點

3.1局部穩定性

定理1當基本再生數R0≤1時,無病平衡點E0是局部漸近穩定的;當R0>1時，無病平衡點E0是不穩定的。

證明無病平衡點E0處的雅可比(Jacobian)矩陣為：

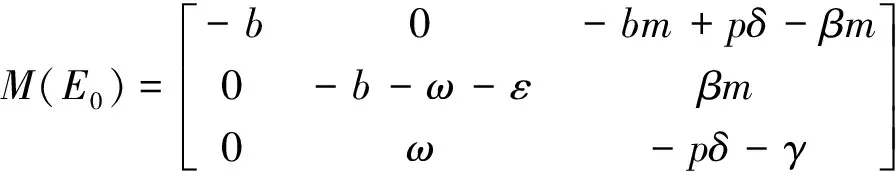
(7)

特征方程為：

(λ+b)(λ2+(pδ+γ+b+ω+ε)λ+(pδ+γ)(b+ω+ε)-βωm)=0;

λ1=-b；

λ2+λ3=-(pδ+γ+b+ω+ε)；

λ2λ3=(pδ+γ)(b+ω+ε)-βωm。

當R0>1時,有βωm>(b+ω+ε)(pδ+γ),所以λ2λ3<0,即λ2,λ3異號,無病平衡點E0是不穩定的。 當R0<1時,有βωm<(b+ω+ε)(pδ+γ),所以λ2λ3>0，又因為λ2+λ3<0,所以λ2,λ3<0,即無病平衡點E0是局部漸近穩定的。

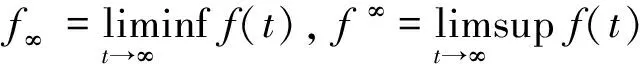
3.2全局穩定性

定理2當R0≤1時,無病平衡點E0是全局漸近穩定的。

(8)

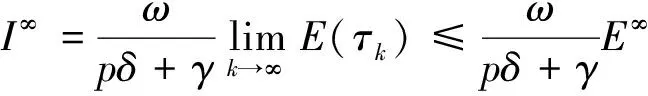
(9)

4　地方病平衡點

4.1局部穩定性

定理3當R0>1時,地方病平衡點E1是局部漸近穩定的。

證明地方病平衡點E1處的雅可比(Jacobian)矩陣為：

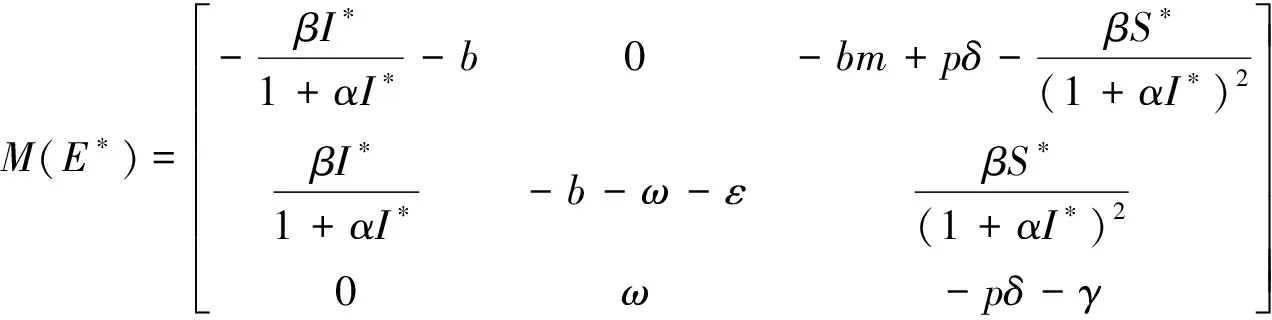
(10)

特征方程為：

a3λ3+a2λ2+a1λ+a0，

(11)

其中：

a3=1；

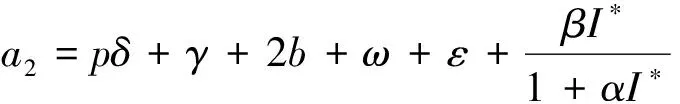
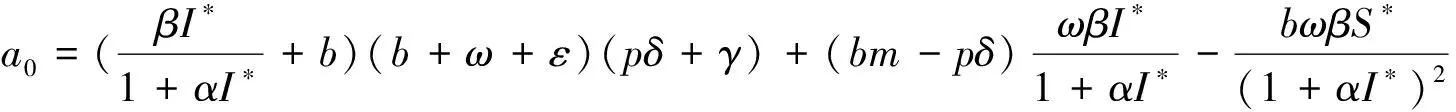
顯然a3>0,a2>0,將式(4)帶入a1和a0化簡可得：

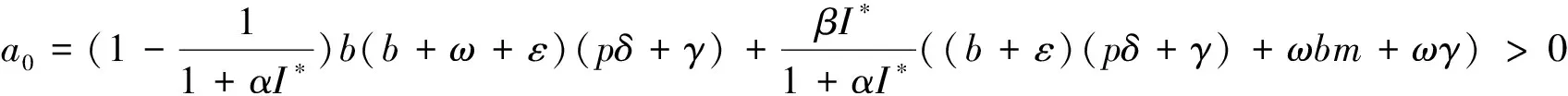
特征方程(11)的赫爾維茨(Hurwitz)行列式為：

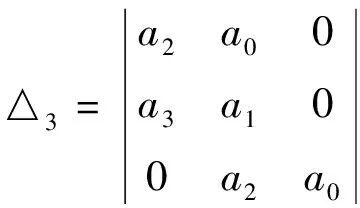
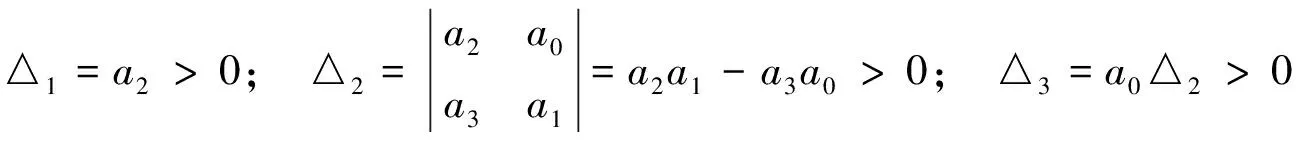
由赫爾維茨(Hurwitz)判據得：特征方程(11)的所有根都具有負實部,所以當R0>1時，平衡點E1是局部漸近穩定的。

4.2全局穩定性

設開集D?Rn,對x∈D,x→f(x)∈Rn是C1函數,考慮微分方程

(12)

設x(t,x0)代表方程(12)滿足條件x(0,x0)=x0的解,集合K稱為方程(12)在D內的吸引集,若對每一個緊子集K1?D,當t充分大時,都有x(t,K1)?K,做如下基本假設：

(H1) 方程(12)在D內存在一個緊的吸引子集K?D。

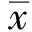
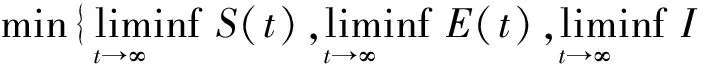
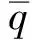
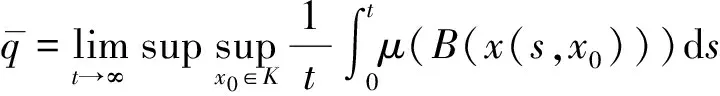
定理4若bm-pδ<0,則當R0>1時,地方病平衡點E1在Ω內部是全局漸近穩定的。

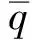
系統(2)的雅可比矩陣為J，

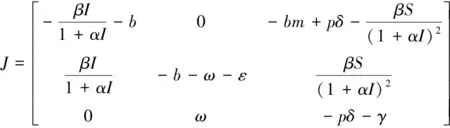
(13)

由文獻[9]知:矩陣J的第二加性復合矩陣為J[2]，

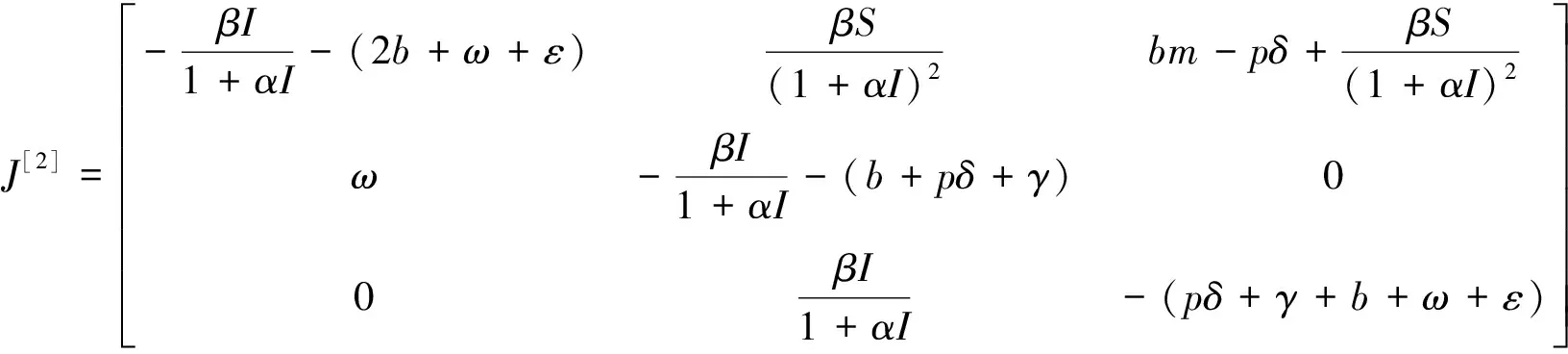
(14)

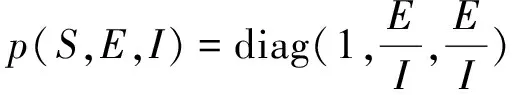
(15)

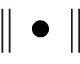
μ(B)≤sup{g1,g2},

(16)

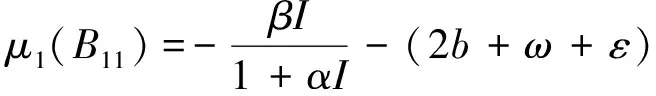
下面計算μ1(B22)。把B22的每一列非對角線上的元素取絕對值,然后加到相應列的對角元素上得:

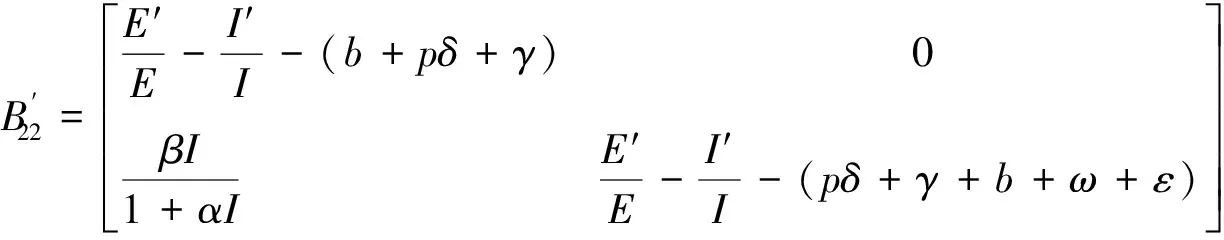
(17)

由系統(2)知:

(18)

定義1中提到的常數c可以經過調整后得到：存在T>0使得E(t)>c,I(t)>c(t>T),其中T與x(0)∈K無關。

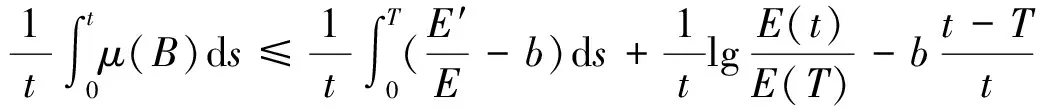
5　結論

(1)當R0≤1時,無病平衡點E0是全局漸近穩定的；當R0>1時，無病平衡點E0是不穩定的。

(2)當R0>1時，地方病平衡點E1是局部漸近穩定的；當bm-pδ<0且R0>1時，地方病平衡點E1是全局漸近穩定的。

[1]商寧寧,王輝,胡志興,等.一類具有飽和發生率和飽和治愈率的SIR傳染病模型的分支分析[J].昆明理工大學學報(自然科學版),2015,40(3):139-148.

[2]HU Z X,MA W B,RUAN S G.Analysis of SIR epidemic models with nonlinear incidence rate and treatment[J].Mathematical biosciences,2012,238(1):12-20.

[3]LIU Z J.Dynamics of positive solutions to SIR and SEIR epidemic models with saturated incidence rates[J].Nonlinear analysis(real world applications),2013,14:1286-1299.

[4]QI L X,CUI J G.The stability of an SEIRS model with nonlinear incidence,vertical transmission and time delay[J].Applied mathematics and computation,2013,221:360-366.

[5]王翠姣,宋燕,王旭輝.一類具有垂直傳染和預防接種的SEIR傳染病模型[J].大學數學,2010,26(4):126-129.

[6]THIEME R H.Persistence under relaxed point-dissipativity (with applications to an endemic model)[J].SIAM journal of mathematical analysis,1993,24(2):407-435.

[7]LI X Z,ZHOU L L.Global stability of an SEIR epidemic model with vertical transmission and saturating contact rate[J].Chaos,solitons and fractals,2009,40:874-884.

[8]LI M,GRAEF J R,WANG L C.Global dynamics of a SEIR model with varying total population size[J].Mathematical biosciences,1990,160(2):191-213.

[9]馬知恩,周義倉,王穩地,等.傳染病動力學的數學建模與研究[M].北京:科學出版社,2004.

[10]FIEDLER M.Additive compound matrices and inequality for eigenvalues of stochastic matrices[J].Czechoslovak mathematical journal,1974,99:392-402.

國家自然科學基金項目(61174209,11471034)

楊彩虹(1991-)，女，山東濱州人，碩士生；胡志興(1962-)，男，陜西漢中人，教授，博士，碩士生導師，主要從事非線性動力系統與混沌、生物數學等方面的研究.

2016-07-28

1672-6871(2017)01-0078-06

10.15926/j.cnki.issn1672-6871.2017.01.016

O175

A