基于分數階自抗擾技術的核電站穩壓器壓力控制*
梁 華, 何柏青(南昌理工學院 電子學院, 南昌 330000)
基于分數階自抗擾技術的核電站穩壓器壓力控制*
梁 華, 何柏青
(南昌理工學院 電子學院, 南昌 330000)
針對傳統PID在復雜的核電站穩壓器控制系統中無法獲得良好的控制效果的問題,提出了分數階自抗擾控制器(FOADRC).該控制器將分數階控制器與自抗擾控制器相結合,不僅具備分數階控制器的快速與高精度特點,還具備自抗擾控制器的強魯棒性和抗擾動性能,解決了ADRC技術中非線性狀態誤差反饋控制律調參較困難的問題.建立的穩壓器壓力控制的Simulink仿真模型表明,分數階自抗擾控制器與傳統PID控制和ADRC控制相比具有更加優良的性能指標.
核電站; 穩壓器; 壓力控制; 分數階PIλDμ控制器; ADRC控制; PID控制; FOADRC控制; Simulink仿真
穩壓器是核電站一回路中的重要設備之一,其作用是調節和維護一回路冷卻劑的壓力,從而保證穩壓器的壓力和水位維持在設定值上.但是穩壓器是一個非常復雜的系統(慣性大,干擾多等),在實際中很難獲得穩壓器的精確模型.因此,利用傳統的控制算法就很難獲得令人滿意的控制效果[1].針對穩壓器的控制,多采用傳統的PID控制,由于其自身局限性,控制效果不是很理想,抗干擾能力也較差.為此,研究人員在分數階理論研究的基礎上,又提出了分數階PIλDμ控制器,其比傳統PID控制器多了積分階次λ和微分階次μ,增加了控制器的靈活度,實現PID由點到面的控制,相比于傳統PID控制,它繼承了傳統PID控制的優點并具有更靈活的結構和更強的魯棒性,其控制律的變化也更加精確,因此,可獲得更優的動態性能和魯棒性能[2].針對PID控制的自身局限性(快速性與超調量的直接矛盾,抗干擾能力差等),研究員韓京清教授提出了自抗擾控制技術,主要由安排過渡過程(TD)、擴張狀態觀測器(ESO)和非線性狀態誤差反饋控制律(NLSEF)等部分組成,其不依賴被控對象的精確數學模型,能夠將系統的未建模動態和未知外界擾動都歸結為對系統的總和擾動而進行估計和補償,可以很好地改善傳統PID控制的不足[3].
本文考慮到分數階PIλDμ控制器和自抗擾控制技術各自的優點,提出了分數階自抗擾控制器(FOADRC),該控制器在分數階PIλDμ控制器的基礎上引入了自抗擾的安排過渡過程和擴張觀測器,使其既具有分數階控制器的快速性和高精度的性能,又具有自抗擾控制器的強魯棒性等.通過理論分析和仿真結果表明,分數階自抗擾控制器(FOADRC)比傳統PID控制和自抗擾控制都具有更加優良的動、靜態性能指標.
1 分數階控制器
1.1 分數階微積分理論
分數階微積分是指微積分的階次不再是整數,可以是分數甚至復數,它可以看作是傳統PID控制的推廣.常用的分數階微積分的定義有三種,分別為Grunwal-Letnikov定義、Riemann-Liouville定義和Caputo定義[4],其中,連續的分數階微積分算子的表達式為
(1)
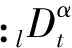
1.2 分數階PIλDμ控制器
分數階PIλDμ控制器是整數階PID控制器的廣義表達式,是將整數階的積分項λ和微分項μ的階次擴展到分數領域,其控制器的輸出可以表示為
u(t)=Kpe(t)+KiDλe(t)+KdDμe(t)
(2)
式中:D為分數階微積分基本操作算子的簡化符號;e(t)為系統誤差;λ為積分階次,λ>0;μ為微分階次,μ>0;Kp、Ki、Kd均為控制器的控制參數,并與整數階PID意義一樣,分別為比例系數、積分系數和微分系數.
經拉普拉斯變換可以得到分數階PIλDμ控制器的傳遞函數,即
G(s)=Kp+Kis-λ+Kdsμ
(3)
式中,s為拉普拉斯算子.
由式(3)可以看出,整數階PID控制器是分數階PIλDμ控制器的積分項λ和微分項μ取特殊值的情況.因此,分數階PIλDμ控制器可以實現PID由點到面的控制,通過合理的參數整定,分數階PIλDμ控制器能更好地、更精確地提高系統控制效果.
1.3 分數階微積分算子的近似與改進
實際上,在分數階微積分的定義下,分數階PIλDμ控制器是一個無限維數的濾波器.為了實現分數階控制,本文采用Oustaloup近似算法以及改進算法,其中,Oustaloup濾波器在一個有限的頻率段(wb,wh)內對微積分算子的近似可表示為
(4)
(5)
(6)

(7)
式中:wh、wb分別為Oustaloup濾波器近似頻率范圍的上下限;N為濾波器的階次.
由于該算法在近似頻率兩端的近似效果不是很理想,因此,本文參考了文獻[5]提出的改進算法,該算法是將分數階算子用分數階傳遞函數近似,即
(8)
式中,m、n為常數,均大于0.在wb (9) 聯合式(8)、(9)可以得到微積分的近似公式,即 (10) 式中,s為拉普拉斯算子,s=jw,j為虛數單位. 自抗擾控制器(ADRC)由非線性跟蹤微分器(TD)、非線性擴張狀態觀測器(ESO)和非線性狀態誤差反饋控制律(NLSEF)三部分組成.該控制策略對經典PID控制做了四個方面的改進:1)安排了過渡過程;2)采用跟蹤微分器對被控對象提取微分信號;3)由非線性擴張觀測器實現擾動的估計和補償;4)由誤差的P、I、D的非線性組合構成非線性PID控制器[6].假設被控對象為 (11) 式中:f(x1,x2)為未知量;b、u為已知量. 以二階ADRC為例介紹其各部分的算法[7],典型二階自抗擾控制器的結構如圖1所示. 圖1 自抗擾控制器的基本結構Fig.1 Basic structure of ADRC 2.1 非線性跟蹤微分器 跟蹤微分器TD為參數輸入安排過渡過程,得到光滑的輸入信號,并提取其微分信號,即向TD輸入信號v(t),可以得到跟蹤信號v1(t)和微分信號v2(t).二階離散形式的非線性微分跟蹤器可描述為 (12) 式中:e為系統誤差;v1為跟蹤信號;v2為微分信號;r為速度因子;h0為濾波因子;fhan()為最優綜合控制函數,其表達式為 (13) (14) 2.2 擴張狀態觀測器 擴張觀測器(ESO)是自抗擾控制器的精髓,擴張觀測器能夠將系統內部和外部擾動均作為系統的擴張狀態變量進行動態觀測和補償,使控制器具有很強的魯棒性.擴張觀測器狀態描述表達式為 (15) 式中:β1、β2、β3為系統參數,均大于零;z1為輸出y的跟蹤信號;z2為輸出的微分信號;z3為對擾動和不確定性的估計量;u為被控對象輸入信號;b為常數;fal()為飽和函數,其作用為抑制信號抖振,其表達式為 (16) 式中,δ通常取值為采樣步長h. 2.3 非線性誤差反饋控制律 針對傳統PID控制形式為P、I、D的線性組合,該方式顯然不是最佳組合形式,可以在非線性范圍內尋找一種更好的組合方式.其中,一種PD形式的非線性組合可描述為 (17) 式中,β11、β12為增益系數,類似于PD控制器的比例系數和微分系數.其中,擾動補償過程為 u=u0-z3/b0 (18) 式中,b0為補償因子.ADRC控制器中的參數包括r0、h0、β1、β2、β3、β11、β12、h1和b0,其中,r0、h0、β1、β2、β3和h1均與系統的采樣步長有關,其關系式[8]為:r0=0.001/h2,h0=5h,β1=1/h,β2=1/(3h2),β3=1/(32h3),h1=10h.增益系數β11、β12與PID控制器中的比例微分作用相當,則有Kp=β11,Kd=β12.補償因子b0相當于PID控制器的積分增益,則有Ki=b0.對于上述參數,本文不能把其當作精確的參數,在實際應用中,應該作為參考值,再在其附近仔細尋找合適的參數. 針對上述兩種控制器的各自優缺點,本文設計了分數階自抗擾控制器(FOADRC).一方面,該控制器利用分數階PIλDμ控制器相角范圍廣、快速性好和精度高等特點來替換傳統ADRC控制器中非線性誤差反饋控制律,用以提高ADRC控制器的性能,同時也克服了非線性誤差反饋控制律帶來的高頻顫振和參數調整困難等問題.由于分數階積分環節的引入,可以改善整數積分環節導致閉環響應速度緩慢,調節時間長,容易產生振蕩,積分飽和引起的控制量飽和等負面影響.另一方面,ADRC中的非線性擴張狀態觀測器可以實現對被控對象擾動誤差的估計補償,同時也增強了分數階PIλDμ控制器的抗干擾能力.本文涉及的分數階自抗擾控制器的結構如圖2所示. 圖2 分數階自抗擾控制器結構Fig.2 Structure of FOADRC 穩壓器壓力控制的原理如圖3所示.該控制系統由PID控制器、函數發生器(加熱器用于升壓,噴淋閥用于降壓)和繼電器(通斷式加熱器和保護閥)等構成,用于壓力的控制.系統的壓力傳感器將不斷檢測壓力信號,實時地跟設定值進行做差對比,并將誤差信號送給常規的PID控制器,從而使相關的設備產生動作.本文將其中的PID控制用分數階自抗擾控制來代替. 圖3 壓力控制系統原理圖Fig.3 Principle diagram of pressure control system 根據上述原理,通過在線辨識能夠得到壓力控制系統的傳遞函數.文獻[9]得出的模型為 (19) 本文針對穩壓器中壓力控制系統分別采用傳統PID控制、ADRC控制和FOADRC控制進行對比分析.其中,PID的參數為Kp=100,Ki=0.11,Kd=500;ADRC的主要參數為r0=0.4,h0=0.05,β11=800,β12=500,β1=20,β2=133.33,β3=33,b0=1.776/3 300;FOADRC中分數階的參數為Kp=13,Ki=90.25,Kd=800,λ=0.85,μ=0.65.通過觀察穩壓器壓力的實際仿真結果可以明顯看出,FOADRC控制與ADRC控制和常規PID控制相比,其超調量減小,而且調節時間、峰值時間和上升時間等都明顯縮短,穩態誤差較小,控制精度較高,具有較好的動態響應性能,能夠提高穩壓器壓力的控制性能,仿真結果和數據如圖4和表1所示. 圖4 壓力控制系統仿真圖Fig.4 Simulation diagram for pressure control system 表1 壓力的動態性能指標比較Tab.1 Comparison in dynamic performanceindexes of pressure 為了驗證本文所設計控制器的魯棒性,在仿真時間為50 s時加入幅值為0.1 MPa的階躍干擾來模擬核電站運行過程中的不確定影響因素,仿真結果如圖5所示.由圖5可知,在受干擾的情況下,傳統PID控制器的超調量較大,且在19.09 s內才完成調節,需調節的時間較長;ADRC控制器的超調量較小,需要2.12 s完成調節;而FOADRC控制器的超調量最小,干擾對控制器的參數影響最小,且在0.035 s內完成調節,說明能更快地回到穩態值.由此說明,FOADRC控制器受負載的影響較小,具有很好的抗干擾性和魯棒性. 圖5 加干擾下的階躍響應Fig.5 Step response with added disturbance 針對復雜時變多干擾的核電站穩壓器,本文將自抗擾控制器(ADRC)與分數階PIλDμ控制器相結合,設計了分數階自抗擾控制器(FOADRC),并首次用于核電站穩壓器壓力的控制系統中.通過實際仿真實現了壓水堆核電站穩壓器壓力的有效控制.通過與傳統PID控制和ADRC控制相對比,無論在跟蹤性還是抗干擾能力方面都大大增強,既具有分數階PIλDμ控制器的快速和高精度的性能,又擁有自抗擾控制器的強魯棒性和抗干擾能力.本文為分數階自抗擾控制器在核電站穩壓器上的應用提供了參考. [1] 張國鐸,楊旭紅,盧棟青,等.核反應堆穩壓器水位和壓力控制系統研究 [J].化工自動化及儀表,2013,40(1):35-38. (ZHANG Guo-duo,YANG Xu-hong,LU Dong-qing,et al.Research on water level and pressure control system of nuclear reactor regulator [J].Control and Instruments in Chemical Industry,2013,40(1):35-38.) [2] 鮑雪,王大志,楊永生.基于CAPSO算法的修正炮彈分數階控制器設計 [J].儀器儀表學報,2015,36 (11):2556-2561. (BAO Xue,WANG Da-zhi,YANG Yong-sheng.Design of the fractional order controller for correction projectiles basedon the improved particle swarm optimization algorithm [J].Chinese Journal of Scientific Instrument,2015,36(11):2556-2561.) [3] 韓京清.自抗擾控制技術:估計補償不確定因素的控制技術 [M].北京:國防工業出版社,2016. (HAN Jing-qing.Active disturbance rejection control technique:the technique for estimating and compensating the uncertainties [M].Beijing:National Defense Industry Press,2016.) [4] 車樹濤.分數階PIλDμ蒸汽壓力控制系統算法研究 [D].哈爾濱:哈爾濱理工大學,2012. (CHE Shu-tao.Research on algorithm of the steam pressure system controled by fractional-order PIλDμ[D].Harbin:Harbin University of Science and Technology,2012.) [5] 吳振宇,趙亮,馮林.基于分數階PID控制器的智能車控制 [J].控制工程,2011,18(3):401-404. (WU Zhen-yu,ZHAO Liang,FENG Lin.Control of intelligent vehicle based on fractional order PID [J].Control Engineering of China,2011,18(3):401-404.) [6] 劉金琨.先進PID控制MATLAB仿真 [M].北京:電子工業出版社,2011. (LIU Jin-kun.Advanced PID control about MATLAB simulation [M].Beijing:Publishing House of Electronics Industry,2011.) [7] 蘇思賢.自抗擾控制器及其應用研究 [D].無錫:江南大學,2011. (SU Si-xian.Active disturbance rejection controller and its application research [D].Wuxi:Jiangnan University,2011.) [8] 陳紅,曾建,王廣軍.蒸汽發生器水位的自抗擾控制 [J].中國電機工程學報,2010,30(32):103-106. (CHEN Hong,ZENG Jian,WANG Guang-jun.Stam generator water level control based on active distur-bance rejection control [J].Proceedings of the CSEE,2010,30(32):103-106.) [9] 林靜.基于自抗擾的核電站穩壓器控制系統研究 [D].上海:上海電力學院,2014. (LIN Jing.Research on control system of pressurizer in nuclear reactor based on active disturbances rejection controller [D].Shanghai:Shanghai University of Electric Power,2014.) Pressurecontrolofpressurizerinnuclearpowerstationbasedonfractionalorderautodisturbancerejectiontechnique LIANG Hua, HE Bo-qing Aiming at the problem that the traditional PID can not obtain good control effect in the complex pressurizer control system of nuclear power station, a fractional order auto disturbance rejection controller (FOADRC) was proposed. Both fractional order controller and auto disturbance rejection controller (ADRC) were combined in the present controller, so that the controller could not only have the rapidity and high precision features of fractional order controller, but also have the strong robustness and disturbance rejection performance of ADRC. Therefore, the problem of difficult parameter adjustment in the nonlinear state error feedback control law in ADRC technology gets solved. The established Simulink simulation model for the pressure control of pressurizer reveals that compared with the traditional PID control and ADRC control, the FOADRC has better performance indexes. nuclear power station; pressurizer; pressure control; fractional order PIλDμcontroller; ADRC control; PID control; FOADRC control; Simulink simulation 2017-03-28. 江西省教育廳教改課題基金資助項目(JXJG-16-25-8). 梁 華(1984-),女,江西南昌人,講師,碩士,主要從事自動化控制和信息處理等方面的研究. * 本文已于2017-10-25 21∶13在中國知網優先數字出版. 網絡出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20171025.2113.046.html 10.7688/j.issn.1000-1646.2017.06.18 TL 361 A 1000-1646(2017)06-0697-05 (責任編輯:鐘 媛 英文審校:尹淑英)2 自抗擾控制技術
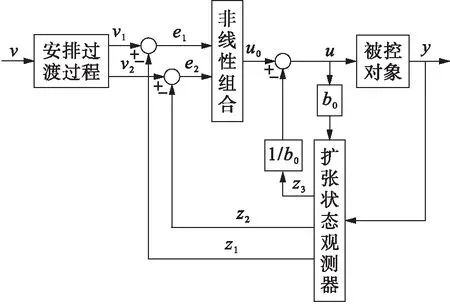
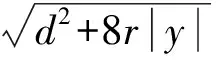
3 分數階自抗擾控制器的設計
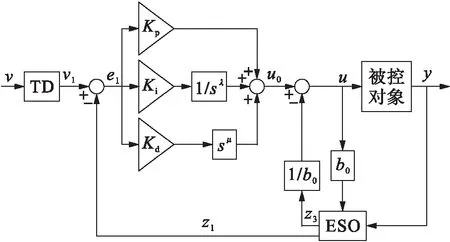
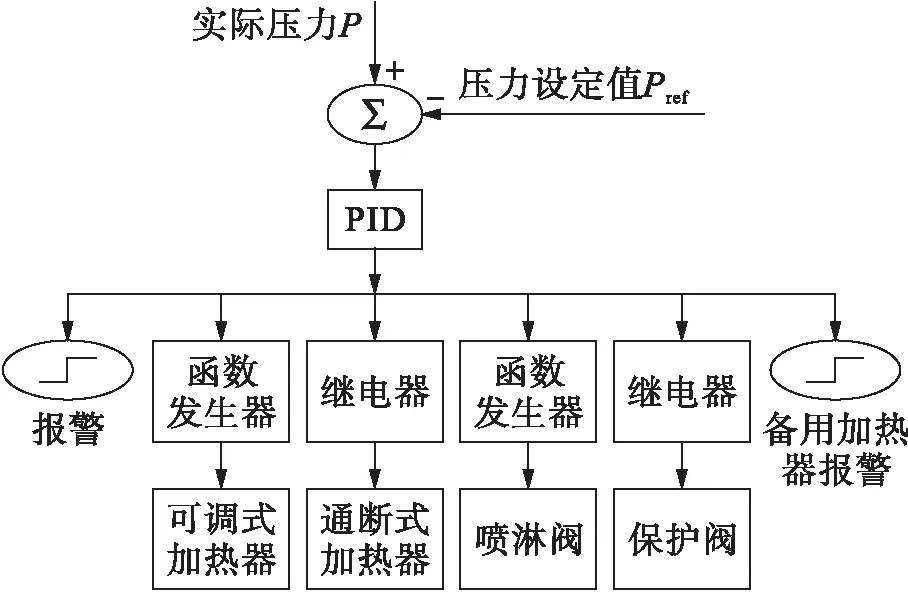
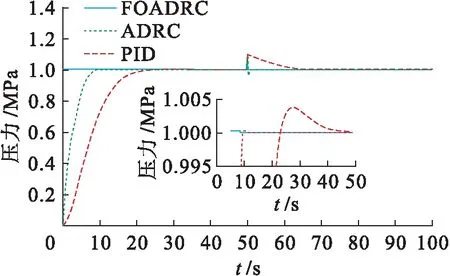
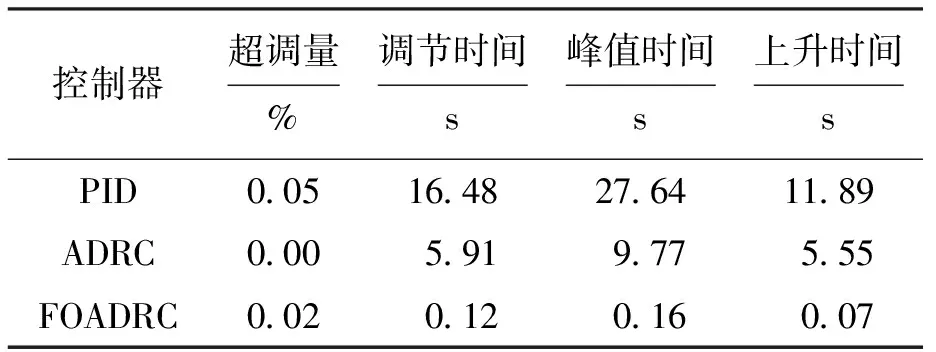
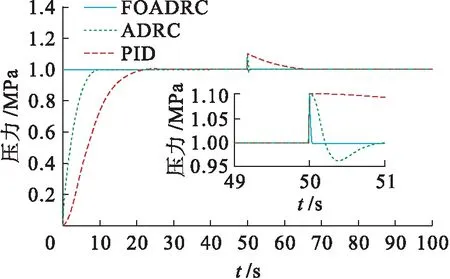
4 系統仿真
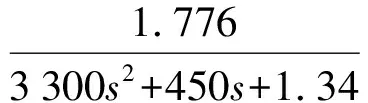
5 結 論
(School of Electronics, Nanchang Institute of Technology, Nanchang 330000, China)

