高維小樣本分類問題中特征選擇研究綜述

王 翔，胡學鋼

(1.合肥工業大學 計算機信息學院，合肥 230009; 2.安徽省科學技術情報研究所 文獻情報分析中心，合肥 230011)(*通信作者電子郵箱wangxiang@ahinfo.gov.cn)

高維小樣本分類問題中特征選擇研究綜述

王 翔1,2*，胡學鋼1

(1.合肥工業大學 計算機信息學院，合肥 230009; 2.安徽省科學技術情報研究所 文獻情報分析中心，合肥 230011)(*通信作者電子郵箱wangxiang@ahinfo.gov.cn)

隨著生物信息學、基因表達譜微陣列、圖像識別等技術的發展，高維小樣本分類問題成為數據挖掘(包括機器學習、模式識別)中的一項挑戰性任務，容易引發“維數災難”和過擬合問題。針對這個問題，特征選擇可以有效避免維數災難，提升分類模型泛化能力，成為研究的熱點，有必要對國內外高維小樣本特征選擇主要研究情況進行綜述。首先分析了高維小樣本特征選擇問題的本質；其次，根據其算法的本質區別，重點對高維小樣本數據的特征選擇方法進行分類剖析和比較；最后對高維小樣本特征選擇研究面臨的挑戰以及研究方向作了展望。

特征選擇；高維數據；小樣本學習；信息過濾；支持向量機

0 引言

隨著科學研究的不斷進步，數據挖掘領域需處理的對象越來越復雜，其數據維度也在急劇增加，在圖像識別、文本分類、生物信息學、基因微陣列分析等大規模數據挖掘應用中出現了一個被稱為高維小樣本學習的研究熱點。

高維小樣本數據，是指具備數據維數特別高，樣本絕對數量很少或樣本數遠小于數據維數特征的數據(也有文獻稱為”Largepsmalln”數據[1]，p代表特征數，n代表樣本數)。

高維小樣本數據上的分類問題是機器學習中的難點，針對不同的應用領域衍生出了高維小樣本、高維稀疏、高維不平衡等多個研究熱點。較高的維數是獲得問題準確描述的有力保障，而難以避免地會含有大量冗余、不相關和噪聲特征，由于高維小樣本數據的這些特點，容易引發“維數災難”(Curse of Dimensionality)，即隨著維數增高，計算復雜度顯著增高而分類器的性能急劇下降；又因為其樣本數量很少，傳統的分類學習方法效能嚴重下降，容易出現過擬合(Over Fitting)，無法進行有效的分類或識別；近年來，高維小樣本導致的特征選擇模型的不穩定性也引起了重視。為了消除或減輕維數災難，同時提升分類器的泛化能力，降維成為重要途徑。

在不同應用領域的高維小樣本降維研究中，特征抽取與特征選擇是兩類非常重要的技術。特征抽取主要是是將高維數據映射到特定的低維空間，而特征選擇可以看作從初始特征空間搜索出一個最優特征子集的過程。

從算法原理上分析，特征抽取是一種基于變換的方法，原數據中的不相關和冗余的特征均在降維中產生作用，影響了分類性能，且新的低維特征空間中特征失去原有的物理解釋，對某些高維小樣本數據分類問題(如癌癥基因分析)而言，很難接受。特征選擇并不改變原特征空間，只是選擇一些分辨力好的特征，組成一個新的低維空間，可以保留原始特征空間大部分性質，對于高維小樣本而言，特征選擇可以去除不相關特征和冗余特征，在一定程度上將噪聲數據對分類器性能的影響降到最低，且選擇的特征可解釋性較好。

特征選擇已成為高維小樣本數據分類問題中的關鍵性步驟，一直是機器學習和數據挖掘研究的熱點之一，新的算法也不斷地被提出，本文對當前已進行的研究進行綜述，嘗試從原理上分析這些算法的區別與聯系，總結各自的優點與不足，并對未來高維小樣本特征選擇的研究進行展望。

1 高維小樣本中的特征選擇

為了便于比較和分析，本文按照評價函數的不同將高維小樣本特征選擇方法分為Filter(篩選法)、Wrapper(封裝法)、Embedded(嵌入式)以及Ensemble(集成法)四類，在實際高維小樣本分類應用中，Embedded方法因其適合處理小樣本問題而受到了諸多研究人員的關注，本文也將針對該類方法作重點分析。

1.1 Filter(篩選法)

Filter(篩選法)通過分析特征子集內部的特點來衡量特征的分類能力，與后面的采用何種分類器無關，這類方法通常需要評價特征相關性的評分函數和閾值判別法來選擇出得分最高的特征子集。通過文獻調研，根據選擇特征子集方式的不同，可以繼續劃分為基于特征排序(Feature Ranking)和基于特征空間搜索(Space Search)兩類。

基于特征排序的方法，其主要思想[2]是：

1)使用評分函數(Scoring Function)對每個特征進行評分，并將所有特征按照得分的降序排列；

2)對每個特征得分進行顯著性檢驗(如p-value等)；

3)通過預先設置的閾值選擇排序前列的具有顯著統計學意義的特征；

4)驗證選擇的最優特征子集,通常使用ROC(Receiver Operating Characteristic)曲線、分類正確率、組相關系數、穩定性等。

基于特征排序方法的核心就是評分函數，表1列舉了高維小樣本分類應用中出現的基于度量樣本群分布之間的差異、基于信息論、基于相關性標準等三類熱門評分函數。

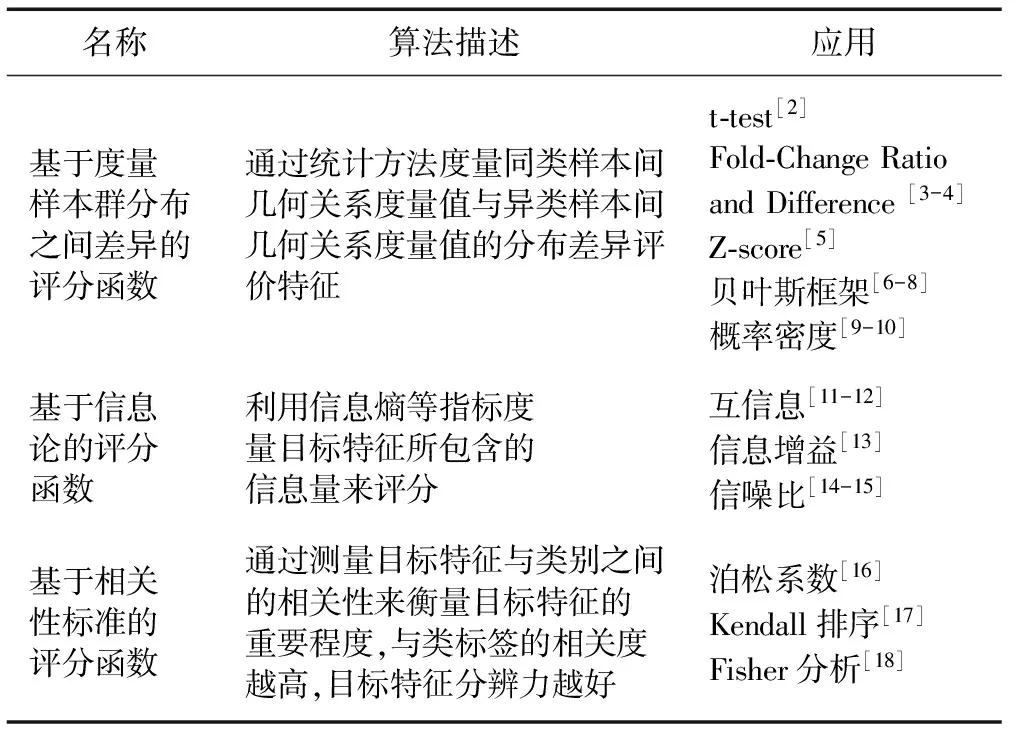
表1 按評分函數分類的基于特征排序方法

基于特征空間搜索法主要是采用一種優化策略從整個特征集合中選出包含最多信息并且達到最小冗余的特征子集。在特定領域，如致病基因的準確發現有一些研究，如基于關聯規則(Correlation-based Feature Selection, CFS)、最大相關最小冗余(Maximum Relevance Minimum Redundancy, MRMR)等，表2給出了上述基于特征空間搜索法的幾類主流方法。

表2 基于特征空間搜索方法

基于特征排序的方法多為單變量方法，每次考慮單個特征的影響，選擇與類標簽最相關的特征，對高維小樣本來說具有較低的計算復雜度，但在某些應用領域如基因微陣列數據中，因忽略了特征間的相互關系，直接應用分類精度較為一般；而基于特征空間搜索為多變量的方法，這類算法不但需要考慮特征子集與類標簽的相關性，還需要考慮特征子集之間的相關性，通常分類正確率較高，但在高維條件下尋找最優子集過程的計算復雜度較高。

1.2 Wrapper(封裝法)

Wrapper方法是一種與分類模型結合的特征選擇方法，使用某個分類模型封裝成黑盒，根據這個分類器在特征子集上的結果好壞來評價所選擇的特征，并采取某些優化的搜索策略對子集進行調整，最終獲得近似的最優子集。N個特征的數據集，可能的特征子集數為2N個，發現最優特征子集已經被證明是NP-Hard，因此高維小樣本特征選擇中Wrapper研究熱點并不局限于采用何種分類模型作為評價準則(通常使用遺傳算法(Genetic Algorithm, GA)[23]、支持向量機(Support Vector Machine, SVM)[24]、K最近鄰(K-Nearest Neighbor,KNN)[25]構建分類模型)，特征子集搜索策略成為研究熱點。

根據文獻[26]，Wrapper方法可以被粗略劃分為順序搜索與啟發式搜索兩類(有文獻將其分類為確定性與隨機性[22])：

1)順序搜索算法。

順序搜索算法從一個空的特征子集開始，通過不斷增加(或刪除)特征直到特征子集能使評價函數得到最好表現，現實中會引入一些停止搜索的標準加速特征子集的選擇，確保評價函數持續增加并達到最好表現時，所選擇特征子集具有最少數目。圖1給出了常規順序搜索算法的發展脈絡。

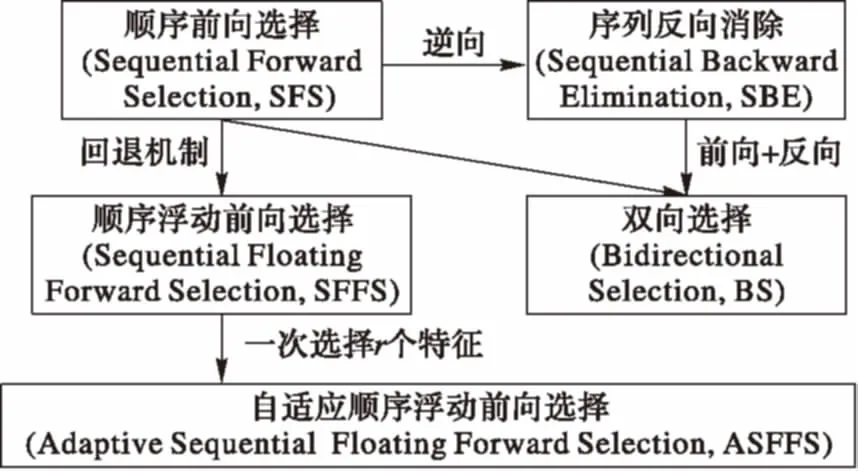
圖1 順序搜索算法發展脈絡

順序搜索策略不斷增加(或刪除)單個特征，避免了完全搜索計算復雜度過高的問題，但選擇出的特征子集很難避免所選特征之間的高度相關性[27]；自適應的順序浮動選擇方法(Adaptive Sequential Floating Forward Selection, ASFFS)[28]引入了參數r用于指定加入特征的數量，并使用參數o去除屬性；同時，為了提升時間性能，Nakariyakul等[29]提出一種新的特征選擇方法——“增L去R”，每次從候選特征集中添加(或刪除)L個特征，考慮入選(或刪除)的L個特征之間相關性，然后刪除(或添加)與類標簽最不相關(或最相關)的R個特征，有效提升了算法的時間性能。

2)啟發式搜索算法。

啟發式搜索算法所開始搜索的初始特征子集是從完整的特征候選集中隨機生成，通過啟發式規則逐步接近最優解，這種方法在搜索時具有很強的不確定性，但隨著算法的運行，使用這種策略獲得的特征子集的質量也能滿足需要。在高維小樣本特征選擇中常用的啟發式搜索方法有GA和粒子群優化(Particle Swarm Optimization, PSO)算法[30]等，通過設定迭代次數的閾值，從而降低需要搜索的特征子集的數量，通過調整GA的參數和遺傳算子，還可以獲得更多的應用。Cordón等[31]使用進化遺傳算法的方法對圖像識別領域中的特征選擇問題進行了嘗試。

因為順序搜索算法的特點，無法從已拋棄的特征中進行二次選擇，也無法拋棄已選擇的特征，容易陷入被稱為嵌套影響(Nesting Effect)的局部最優情況，啟發式搜索算法可以有效解決這些問題，并且有文獻表明，采用并行設計啟發式搜索算法的計算復雜度比順序選擇算法顯著降低[32]。

1.3 Embedded(嵌入式)

Embedded(嵌入式)方法的出現主要是為了解決Wrapper(封裝法)在處理不同數據集時，分類模型需要重構代價高等問題。如果嚴格區分，它與Wrapper的不同在于，Embedded將特征選擇與分類模型的學習過程結合，即在分類器的訓練過程中包含了特征選擇功能，由于其高效的時空性能及較好的分類精度，逐漸成為高維小樣本特征選擇的熱點方向，其中，有兩類方法成為非常熱門的研究對象：一是以SVM為基礎的模型；二是以套索算法Lasso(Least Absolute absolute Shrinkage shrinkage and Selection selection Operator)為代表的正則化組稀疏模型。

由于SVM可以根據有限的樣本在模型的復雜性和學習能力之間尋求最佳平衡，弱化了對數據正態分布的要求，同時對維數災難不敏感，可以有效剔除冗余特征，具有較好的泛化性能，因而被廣泛用于處理高維小樣本特征選擇。

Guyon等[33]采用基于遞歸特征的后項搜索剔除思想(Recursive Feature Elimination, RFE)，提出SVM-RFE方法，該方法將SVM超平面的每個維度對應高維小樣本數據集里的每個特征，從而每個維度權重的絕對值可以用來度量對應數據特征的重要性，即通過權重對特征進行降序排序。從排序后的特征集合開始，每次刪除排名靠后的一個特征，迭代直到該特征集合為空，一般來說最先被刪除的多為噪聲或冗余特征，最后被刪除的特征一般具有較強的區分能力，由于該方法在處理高維小樣本數據方面的優勢及貪婪算法帶來的計算復雜度，圍繞該方法研究人員提出了許多改良方法，其中有按比例刪除特征的[34-35]，采用前向序列思想的[36-37]，采用模糊聚類的[38]，基于Relief的[39]以及采用了粒子群算法的[40]，圖2給出了部分基于SVM-RFE的算法分類。

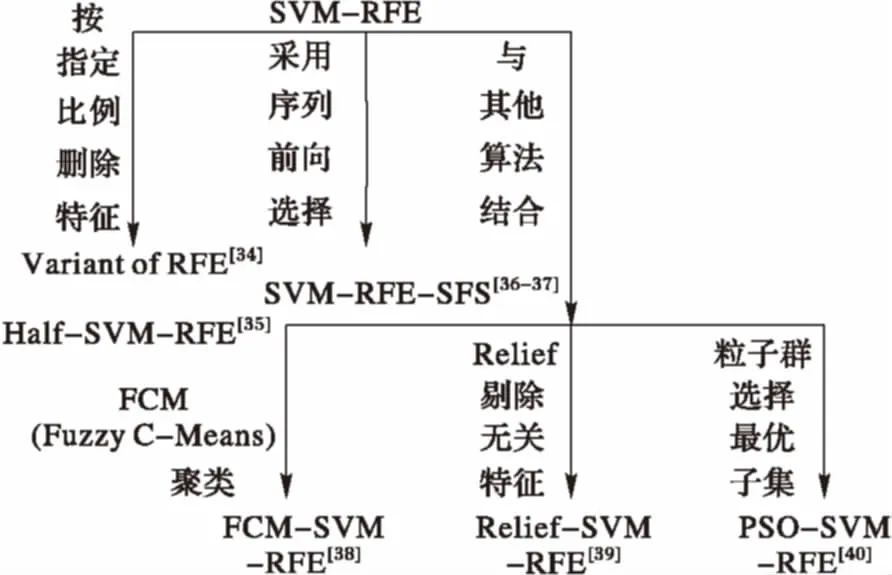
圖2 基于SVM-RFE的算法分類

除基于SVM的方法之外，正則化稀疏模型可以將大量冗余或噪聲特征去除，同時保留與類標變量最相關的特征，選擇的特征子集具有很好的可解釋性，也獲得了許多研究人員的關注。其代表算法有1996年Tibshirani[41]提出的Lasso，其基本思想是在最小二乘估計中加入系數的絕對值作為懲罰項，使系數的絕對值之和小于等于某一個閾值來最小化殘差平方，能產生趨于0的回歸系數，使得與目標關系弱的預測變量(特征)系數被懲罰為0，從而具備特征選擇功能。表3給出了Lasso在高維小樣本數據應用中的優勢和不足。

表3 Lasso在高維小樣本中的優勢與不足

為了解決Lasso的有偏估計問題，自適應Lasso、松弛Lasso、SCAD(Smoothly Clipped Absolute Deviation )模型、MCP(Minimax Concave Penalty)等模型[42-43]相繼被提出。

由于缺少高效的求解算法，Lasso在高維小樣本特征選擇研究中沒有廣泛流行， 最小角回歸(Least Angle Regression, LAR)算法[44]的出現有力促進了Lasso在高維小樣本數據中的應用，后續研究人員從降低計算復雜度及避免過擬合等角度對Lasso進行了改進，如采用迭代思想的GSIL(Gene Selection based on Iterative Lasso)，采用序貫思想的SLasso(Sequential Lasso)以及采用有監督組Lasso(Supervised Group Lasso, SGLasso)等。表4給出了部分針對Lasso缺點的改進方法及其基本思想。

1.4 Ensemble(集成法)

集成學習是使用一系列特征選擇方法進行學習，并使用某種規則把各個學習結果進行整合從而獲得比單個特征選擇方法更好學習效果的高維小樣本特征選擇方法。在某些高維小樣本特征選擇問題研究中，學者多采用這類方法提升特征選擇算法的穩定性，如Li等[52]提出一種新的特征選擇方法，采用重抽樣技術把數據擾動，生成幾個不同的訓練集和測試集，反復調用遞歸決策樹，并把分類錯誤率作為評價指標來選擇特征；Dutkowski等[53]將不同特征選擇算法用于基因選擇，并通過優化策略來整合各個算法得到的結果，形成最終的特征子集；Saeys等[54]、Abeel等[55]將Bagging思想用于集成特征選擇，Saeys采用融合多個特征選擇算法結果的方式來完成特征子集的集成，而Abeel則通過樣本重取樣技術生成多個特征子集，并在若干高維小樣本數據集上與SVM-RFE方法進行對比，取得較好效果。

表4 針對Lasso的改進算法

1.5 特征選擇方法總結

高維小樣本特征選擇難點在于在有限的樣本空間內盡量剔除冗余特征及噪聲數據、盡量選擇分辨能力更好的特征、保證算法的穩定性，同時還需要避免過擬合及綜合考慮時空性能。表5給出了四類特征選擇方法在高維小樣本應用中的優缺點對比。

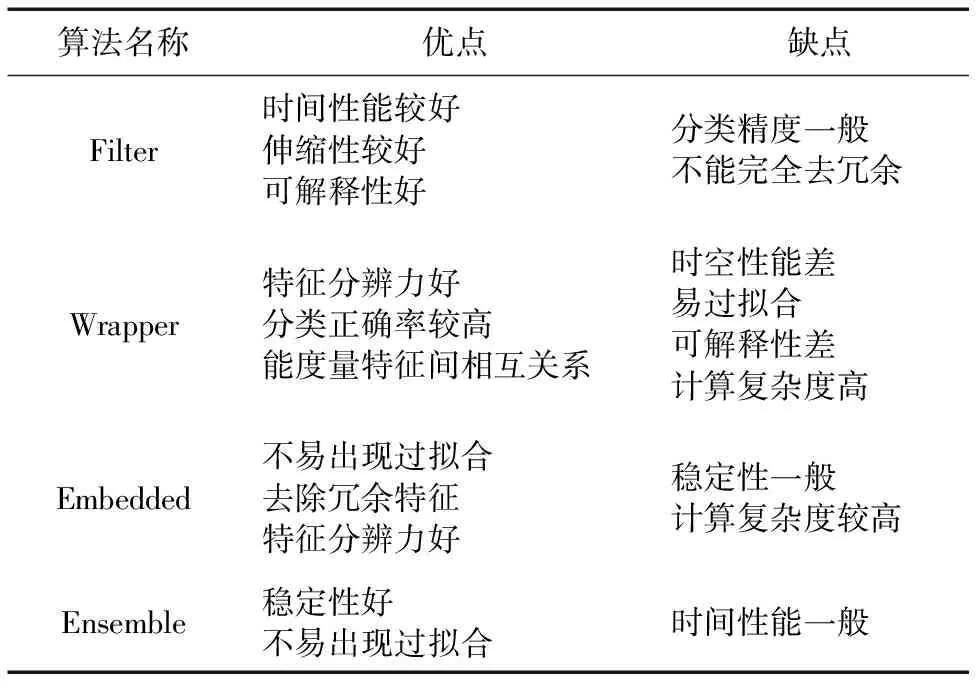
表5 四類特征選擇方法優缺點對比

在實際應用中，SVM和以Lasso為代表的正則化方法是比較常見的方法，特別是SVM方法由于其產生的分類器結構簡單，用到的樣本信息很少，受到了更多的關注，在一些文獻中也有將兩者結合共同進行特征選擇的研究[25]。在近期的文獻中，已較少見到Filter和Wrapper單獨作為高維小樣本的特征選擇模型，常見的多將其應用于兩階段的特征選擇，如使用計算復雜度較低的Filter方法去除冗余與噪聲特征，選擇與類標簽相關度較好的特征構成新的特征集合，再用Wrapper方法(如 SVM、GA、隨機森林)在新的特征集合上去選擇分辨力非常強的特征子集，可以實現很好的降維效果[56-58]，而集成法則更多用于需要算法具備較好穩定性的應用中，對原本就穩定的特征選擇方法，集成后效果并不明顯。

2 挑戰與研究展望

2.1 面臨的挑戰

1)數據不一致，各算法很難直接比較。

高維小樣本特征選擇多源自數據驅動，以基因微陣列數據為例，各研究人員使用的數據來源不盡相同，甚至有同名數據集但內容不相同的情況[59]，這使得后續研究人員很難在統一的數據標準下重現目標算法來進行結果的比較。

2)分類正確率是否仍然是唯一重要指標。

傳統特征選擇方法有很多評價指標，在高維小樣本環境中，有相當一部分文獻在作算法對比分析時，僅僅進行了分類精度的度量，較少涉及算法穩定性、結果可解釋性等度量。

除此之外，面對不平衡高維小樣本數據，特別是在一些代價敏感學習問題中，降低決策風險、減小平均誤分類代價和提高分類可靠性顯得尤為重要，分類正確率是否依然作為特征選擇唯一的重要的評判標準還應具體問題具體對待。

3)復雜且超高維數據帶來巨大壓力。

目前主流的特征選擇方法SVM及Lasso等在處理連續型數據時具有較好的優勢，隨著大數據技術的不斷發展，數十萬維且混合了離散和連續型數值的數據集將有可能成為高維小樣本領域最常見的對象，個別數據甚至可能超過千萬維，復雜且超高維數據的到來給未來特征選擇方法不但在時間和空間復雜度方面提出了巨大挑戰，更在算法本身的設計方面提出了新的要求。

4)缺少國內可信數據源。

目前學界使用的大多為國外機構提供的分析數據，缺少國內公開的權威數據源，特別是基因微陣列數據及人像識別等領域，據此分析的結果得出的結論(如哪些基因對疾病診斷有幫助)很難在實踐中得到驗證，各算法得出的最終結果的可解釋性受到一定影響。

5)缺少對特征選擇結果的解釋分析。

大多數文獻采取與其他文獻中算法進行量化的對比分析來說明自己算法的優勢，很少有文獻針對特征選擇的最終結果，即最終選擇的特征集合的物理屬性進行深入分析，僅通過文獻的閱讀很難了解這些被選擇出的屬性是否可以用于指導實踐，特征選擇結果的可解釋性無從考證。

2.2 未來研究展望

隨著大數據時代的不斷演變，高維數據的價值越來越凸顯，高維小樣本特征選擇主要面臨計算復雜度、時間復雜度和復雜數據類型等問題，結合文獻調研及趨勢分析，本文認為面向高維小樣本的特征選擇方法還可以在以下幾個方面取得新的進展：

1)增量式學習算法(Incremental Learning)。

在未來超高維小樣本數據面前，常規的集中式特征選擇方法可能很難滿足時空性能的需求，甚至無法得到令人滿意的特征選擇結果，增量式學習為超高維小樣本數據的特征選擇問題提供了一種思路，增量式不僅指數量的逐漸遞增，更多的是指特征數量的逐漸遞增。目前，已有工作開展了相關研究，形成了被稱為“Online Feature Selection”的研究熱點。

2)非連續型數據的處理。

當前高維小樣本特征選擇所面對的數據對象很大一部分是連續型數據，特別是基因微陣列數據都是細胞內mRNA 的相對或絕對數量來表示的連續型數據，相應的，大多數文獻都選擇了SVM或Lasso等可以直接處理連續型數據的特征選擇方法，就本文所調研范圍，少有文獻去深入分析高維小樣本連續型數據的離散化問題。因此，對非連續型數據的特征選擇及與連續型數據特征選擇方法進行深度對比分析具有一定研究價值。

3)算法的穩定性(Stability)與可伸縮性(Scalability)。

Lasso等正則化的稀疏模型存在特征選擇的不一致性，即模型稀疏化后的不穩定性，同樣的問題也可能出現在其他幾類主流的特征選擇方法中，由于高維小樣本數據的特殊性，今后的研究可能不單純只進行分類正確率及時空性能的比較，還需要考慮算法本身的穩定性，這樣選擇的結果才更加容易被接受；同時，隨著數據維數的急劇增加，算法的可伸縮性也是一個重要的指標，隨著數據量和維數的增加，算法的性能不可出現顯著下降。

4)傳統統計學算法煥發新生。

正則化方法產生于1955年，Lasso也是20年前的方法，這些傳統的方法在高維小樣本等新的應用環境里重新獲得了發展，這也提示傳統的統計學中的變量選擇方法是否值得去重新梳理，特別是一些線性計算，空間復雜度低的方法，挖掘和改進使之與當前高維小樣本應用能夠結合，從而豐富高維小樣本的特征選擇方法。

5)多階段的混合式特征選擇。

在高維小樣本的應用中，通常伴有高維不平衡、高維稀疏等現象，沒有一種通用的方法可以應對所有的高維小樣本分類應用問題，采用混合的多階段的特征選擇方法，可以有效去除不相關及冗余特征，如使用重抽樣技術擴大樣本規模，使用Filter去除不相關屬性，再使用Embedded等方法去除冗余屬性等。

6)可信數據源的構建。

隨著政府開放數據帶來的利好，國內會有更多專業機構參與國內數據的采集整理工作，如果能根據權威公開數據構建高維小樣本數據開放共享平臺，讓更多研究人員參與其中，可以更好地發揮數據本身的價值。

References)

[1] ESPEZUA S, VILLANUEVA E, MACIEL C D, et al. A projection pursuit framework for supervised dimension reduction of high dimensional small sample datasets [J]. Neurocomputing, 2015, 149(PB): 767-776.

[2] LAZAR C, TAMINAU J, MEGANCK S, et al. A survey on filter techniques for feature selection in gene expression microarray analysis [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1106-1119.

[3] TAO H, BAUSCH C, RICHMOND C, et al. Functional genomics: expression analysis of Escherichia coli growing on minimal and rich media [J]. Journal of Bacteriology, 1999, 181(20): 6425-6440.

[4] KERR M K, MARTIN M, CHURCHILL G A. Analysis of variance for gene expression microarray data [J]. Journal of Computational Biology, 2000, 7(6): 819-837.

[5] THOMAS J G, OLSON J M, TAPSCOTT S J, et al. An efficient and robust statistical modeling approach to discover differentially expressed genes using genomic expression profiles [J]. Genome Research, 2001, 11(7): 1227-1236.

[6] EFRON B, TIBSHIRANI R, STOREY J D, et al. Empirical Bayes analysis of a microarray experiment [J]. Journal of the American Statistical Association, 2001, 96(456): 1151-1160.

[7] LONG A D, MANGALAM H J, CHAN B Y, et al. Improved statistical inference from DNA microarray data using analysis of variance and a Bayesian statistical framework [J]. Journal of Biological Chemistry, 2001, 276(23): 19937-19944.

[8] BALDI P, LONG A D. A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes [J]. Bioinformatics, 2001, 17(6): 509-519.

[9] PARZEN E. On estimation of a probability density function and mode [J]. The Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.

[10] WILINSKI A, OSOWSKI S, SIWEK K. Gene selection for cancer classification through ensemble of methods [C]// Proceedings of the 9th International Conference on Adaptive and Natural Computing Algorithms. Berlin: Springer, 2009: 507-516.

[11] STEUER R, KURTHS J, DAUB C O, et al. The mutual information: detecting and evaluating dependencies between variables [J]. Bioinformatics, 2002, 18(Suppl. 2): S231-S240.

[12] LIU X, KRISHNAN A, MONDRY A. An entropy-based gene selection method for cancer classification using microarray data [J]. BMC Bioinformatics, 2005, 6(1): 1-14.

[13] CHUANG L Y, KE C H, CHANG H W, et al. A two-stage feature selection method for gene expression data [J]. Omics: a Journal of Integrative Biology, 2009, 13(2): 127-137.

[14] GOLUB T R, SLONIM D K, TAMAYO P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring [J]. Brain Research, 1999, 501(2): 205-214.

[15] 李穎新，李建更，阮曉鋼.腫瘤基因表達譜分類特征基因選取問題及分析方法研究[J].計算機學報,2006,29(2):324-330.(LI Y X, LI J G, RUAN X G. Study of informative gene selection for tissue classification based on tumor gene expression profiles [J]. Chinese Journal of Computers, 2006, 29(2): 324-330.)

[16] VAN’T VEER L J, DAI H, VAN DE VIJVER M J, et al. Gene expression profiling predicts clinical outcome of breast cancer [J]. Nature, 2002, 415(6871): 530-536.

[17] PARK P J, PAGANO M, BONETTI M. A nonparametric scoring algorithm for identifying informative genes from microarray data [EB/OL]. [2016- 12- 17]. http://xueshu.baidu.com/s?wd=paperuri%3A%286c6a741e996db71f799147979ac19d70%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdx.doi.org%2F10.1142%2F9789814447362_0006&ie=utf-8&sc_us=5571940567161427371.

[18] CHENG Q, ZHOU H, CHENG J. The Fisher-Markov selector: fast selecting maximally separable feature subset for multiclass classification with applications to high-dimensional data [J]. IEEE Transactions on Pattern Analysis and Machine intelligence, 2011, 33(6): 1217-1233.

[19] WANG Y, TETKO I V, HALL M A, et al. Gene selection from microarray data for cancer classification—a machine learning approach [J]. Computational Biology & Chemistry, 2005, 29(1):37-46.

[20] DING C, PENG H. Minimum redundancy feature selection from microarray gene expression data [J]. Journal of Bioinformatics and Computational Biology, 2005, 3(2): 185-205.

[21] XING E P, JORDAN M I, KARP R M. Feature selection for high-dimensional genomic microarray data [C]// Proceedings of the 18th International Conference on Machine Learning. San Francisco, CA: Morgan Kaufmann, 2001: 601-608.

[22] HIRA Z M, AGILLIES D F. A review of feature selection and feature extraction methods applied on microarray data [J]. Advances in Bioinformatics, 2015, 2015: Article ID 198363.

[23] LI L, WEINBERG C R, DARDEN T A, et al. Gene selection for sample classification based on gene expression data: study of sensitivity to choice of parameters of the GA/KNN method [J]. Bioinformatics, 2001, 17(12): 1131-1142.

[24] CHANDRASHEKAR G, SAHIN F. A survey on feature selection methods [J]. Computers & Electrical Engineering, 2014, 40(1): 16-28.

[25] XIA X L, XING H, LIU X. Analyzing kernel matrices for the identification of differentially expressed genes [J]. PLOS ONE, 2013, 8(12): e81683.

[26] OSAREH A, SHADGAR B. Machine learning techniques to diagnose breast cancer [C]// Proceedings of the 2010 5th International Symposium on Health Informatics and Bioinformatics. Piscataway, NJ: IEEE, 2010: 114-120.

[27] 張靖.面向高維小樣本數據的分類特征選擇算法研究[D].合肥:合肥工業大學,2014:15,35-52.(ZHANG J. Classification and feature selection on high-dimensional and small-sampling data [D]. Hefei: Hefei University of Technology, 2014: 15,35-52.)

[28] SUN Y, BABBS C F, DELP E J. A comparison of feature selection methods for the detection of breast cancers in mammograms: adaptive sequential floating search vs. genetic algorithm [C]// Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society. Piscataway, NJ: IEEE, 2006: 6532-6535.

[29] NAKARIYAKUL S, CASASENT D P. An improvement on floating search algorithms for feature subset selection [J]. Pattern Recognition, 2009, 42(9): 1932-1940.

[30] CHUANG L Y, YANG C H, LI J C, et al. A hybrid BPSO-CGA approach for gene selection and classification of microarray data [J]. Journal of Computational Biology: A Journal of Computational Molecular Cell Biology, 2012, 19(1): 68-82.

[32] KAMYAB S, EFTEKHARI M. Feature selection using multimodal optimization techniques [J]. Neurocomputing, 2016, 171(C): 586-597.

[33] GUYON I, WESTON J, BARNHILL S, et al. Gene selection for caner classification using support vector machines [J]. Machine Learning, 2002, 46(1): 389-422.

[34] DING Y, WILKINS D. Improving the performance of SVM-RFE to select genes in microarray data [J]. BMC Bioinformatics, 2006, 7(Suppl 2): S12.

[35] MAO Y, PI D, LIU Y, et al. Accelerated recursive feature elimination based on support vector machine for key variable identification [J]. Chinese Journal of Chemical Engineering, 2006, 14(1): 65-72.

[36] 謝娟英，謝維信.基于特征子集區分度與支持向量機的特征選擇算法 [J].計算機學報,2014,37(8):1704-1718.(XIE J Y, XIE W X. Several feature selection algorithms based on the discernibility of a feature subset and support vector machines [J]. Chinese Journal of Computers, 2014, 37(8): 1704-1718.)

[37] 游偉,李樹濤,譚明奎.基于SVM-RFE-SFS的基因選擇方法[J].中國生物醫學工程學報,2010,29(1):93-99.(YOU W, LI S T, TAN M K. Gene selection method based on SVM-RFE-SFS [J]. Chinese Journal of Biomedical Engineering, 2010, 29(1): 93-99.)

[38] TANG Y, ZHANG Y Q, HUANG Z. FCM-SVM-RFE gene feature selection algorithm for leukemia classification from microarray gene expression data [C]// Proceedings of the 14th IEEE International Conference on Fuzzy Systems. Piscataway, NJ: IEEE, 2005: 97-101.

[39] 吳紅霞，吳悅，劉宗田,等.基于Relief和SVM-RFE的組合式SNP特征選擇[J].計算機應用研究,2012,29(6):2074-2077.(WU H X, WU Y, LIU Z T, et al. Combined SNP feature selection based on Relief and SVM-RFE [J]. Application Research of Computers, 2012, 29(6): 2074-2077.)

[40] 林俊，許露，劉龍.基于SVM-RFE-BPSO算法的特征選擇方法[J].小型微型計算機系統,2015,36(8):1865-1868.(LIN J, XU L, LIU L. Feature selection method based on SVM-RFE and particle swarm optimization [J]. Journal of Chinese Computer Systems, 2015, 36(8): 1865-1868.)

[41] TIBSHIRANI R. Regression shrinkage and selection via the Lasso [J]. Journal of the Royal Statistical Society, 1996, 58(1): 267-288.

[42] 劉建偉，崔立鵬，劉澤宇,等.正則化稀疏模型[J].計算機學報,2015, 38(7): 1307-1325. (LIU J W, CUI L P ,LIU Z Y, et al. Survey on the regularized sparse models[J]. Chinese Journal of Computers. 2015, 38(7): 1307-1325.)

[43] 劉建偉，崔立鵬，羅雄麟. 結構稀疏模型及其算法研究進展[J].計算機科學,2016,43(S1):1-16.(LIU J W, CUI L P, LUO X L. Research and development on structured sparse models and algorithms [J]. Computer Science, 2016, 43(S1): 1-16.)

[44] EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression [J]. Annals of Statistics, 2004, 32(2): 407-451.

[45] 張靖，胡學鋼，張玉紅,等.K-split Lasso:有效的腫瘤特征基因選擇方法[J].計算機科學與探索,2012,6(12):1136-1143.(ZHANG J, HU X G, ZHANG Y H, et al. K-split Lasso: an effective feature selection method for tumor gene expression data [J]. Journal of Frontiers of Computer Science and Technology, 2012, 6(12): 1136-1143.)

[46] 施萬鋒，胡學鋼，俞奎.一種面向高維數據的均分式Lasso特征選擇方法[J].計算機工程與應用,2012,48(1):157-161.(SHI W F, HU X G, YU K. K-part Lasso based on feature selection algorithm for high-dimensional data [J]. Computer Engineering and Applications, 2012, 48(1): 157-161.)

[47] 施萬鋒，胡學鋼，俞奎. 一種面向高維數據的迭代式Lasso特征選擇方法[J]. 計算機應用研究,2011,28(12):4463-4466.(SHI W F, HU X G, YU K. Iterative Lasso based on feature selection for high dimensional data [J]. Application Research of Computers, 2011, 28(12): 4463-4466.)

[48] ZOU H, HASTIE T. Regularization and variable selection via the elastic net [J]. Journal of the Royal Statistical Society, 2005, 67(2): 301-320.

[49] LUO S, CHEN Z. Sequential Lasso cum EBIC for feature selection with ultra-high dimensional feature space [J]. Journal of the American Statistical Association, 2014, 109(507): 1229-1240.

[50] CHEN Z H. Sequential Lasso for feature selection with ultra-high dimensional feature space [EB/OL]. [2016- 11- 25]. http://www.stat.nus.edu.sg/～stachenz/T11-455R1.pdf.

[51] MA S, SONG X, HUANG J. Supervised group Lasso with applications to microarray data analysis [J]. BMC Bioinformatics, 2007, 8(1):1-17.

[52] LI X, RAO S, WANG Y, et al. Gene mining: a novel and powerful ensemble decision approach to hunting for disease genes using microarray expression profiling [J]. Nucleic Acids Research, 2004, 32(9): 2685-2694.

[53] DUTKOWSKI J, GAMBIN A. On consensus biomarker selection [J]. BMC Bioinformatics, 2007, 8(Suppl 5): S5.

[54] SAEYS Y, ABEEL T, PEER Y V D. Robust feature selection using ensemble feature selection techniques [C]// Proceedings of the European conference on Machine Learning and Knowledge Discovery in Databases, LNCS 5212. Berlin: Springer, 2008: 313-325.

[55] ABEEL T, HELLEPUTTE T, VAN DE PEER Y, et al. Robust biomarker identification for cancer diagnosis with ensemble feature selection methods [J]. Bioinformatics, 2010, 26(3): 392-398.

[56] WANG Y, MAKEDON F S, FORD J C, et al. HykGene: a hybrid approach for selecting marker genes for phenotype classification using microarray gene expression data [J]. Bioinformatics, 2005, 21(8): 1530-1537.

[57] AKADI A E, AMINE A, OUARDIGHI A E, et al. A two-stage gene selection scheme utilizing MRMR filter and GA wrapper [J]. Knowledge and Information Systems, 2011, 26(3): 487-500.

[58] BERMEJO P, DE LA OSSA L, GMEZ J A, et al. Fast wrapper feature subset selection in high-dimensional datasets by means of filter re-ranking [J]. Knowledge-Based Systems, 2012, 25(1): 35-44.

[60] 姚唐龍.基因表達譜數據挖掘的特征提取方法研究[D].合肥:安徽大學,2015:13-19.(YAO T L. Research on feature extraction method of gene expression profiles data mining [D] . Hefei: Anhui University, 2015: 13-19.)

Overviewonfeatureselectioninhigh-dimensionalandsmall-sample-sizeclassification

WANG Xiang1,2*, HU Xuegang1

(1.SchoolofComputerandInformation,HefeiUniversityofTechnology,HefeiAnhui230009,China;2.LiteratureInformationAnalysisDepartment,AnhuiInstituteofScientificandTechnicalInformation,HefeiAnhui230011,China)

With the development of bioinformatics, gene expression microarray and image recognition, classification on high-dimensional and small-sample-size data has become a challenging task in data ming, machine learning and pattern recognition as well. High-dimensional and small-sample-size data may cause the problem of “curse of dimensionality” and overfitting. Feature selection can prevent the “curse of dimensionality” effectively and promote the generalization ability of classification mode, and thus become a hot research topic. Accordingly, some recent development of world-wide research on feature selection in high-dimensional and small-sample-size classification was briefly reviewed. Firstly, the nature of high-dimensional and small-sample feature selection was analyzed. Secondly, according to their essential difference, feature selection algorithms for high-dimensional and small-sample-size classification were divided into four categories and compared to summarize their advantages and disadvantages. Finally, challenges and prospects for future trends of feature selection in high-dimensional small-sample-size data were proposed.

feature selection; high-dimensional data; small-sample-size learning; information filtering; Support Vector Machine (SVM)

2017- 03- 27;

2017- 04- 21。

國家973計劃項目(2016YFC0801406)；國家自然科學基金資助項目(61673152)；安徽省自然科學基金資助項目(1408085QF136)。

王翔(1982—)，男，安徽合肥人，博士研究生，主要研究方向：數據挖掘、人工智能、情報分析； 胡學鋼(1962—)，男，安徽合肥人，教授，博士，主要研究方向：數據挖掘、人工智能、大數據分析。

1001- 9081(2017)09- 2433- 06

10.11772/j.issn.1001- 9081.2017.09.2433

TP391.4

A

This work is partially supported by the National Basic Research Program (973 Program) of China (2016YFC0801406), the National Natural Science Foundation of China (61673152), the Natural Science Foundation of Anhui Province (1408085QF136).

WANGXiang, born in 1982, Ph. D. candidate. His research interests include data mining, artificial intelligence, intelligence analysis.

HUXuegang, born in 1962, Ph. D., professor. His research interests include data mining, artificial intelligence, big data analysis.