以橢圓為例研究圓錐曲線的由來及其解析定義
江西省宜春中學2018屆高三(22)班 宋 禹
以橢圓為例研究圓錐曲線的由來及其解析定義
江西省宜春中學2018屆高三(22)班 宋 禹
高中數學教材將橢圓、雙曲線、拋物線歸在圓錐曲線章節中,這在當時給我及許多初學的同學帶來了一些疑惑。不管是第一定義、第二定義還是性質與判斷,這三種曲線似乎都與圓錐并無聯系,為什么它們會被命名為圓錐曲線呢?
為了解開這個疑惑,筆者查閱資料研究圓錐曲線的發展歷史。原來,最初這幾種曲線就是用平面切割圓錐得到的,故命名為圓錐曲線。在2000多年前,古希臘數學家阿波羅尼斯在他的著作《圓錐曲線》中,記載了用不同角度的平面去截一個二次錐面,得到的交線中就包括橢圓、雙曲線、拋物線及一些退化情形(圓和直線)。而我們現在所熟知的圓錐曲線的定義和性質,是在16世紀以后才由數學家們陸續發現的,之后對于圓錐曲線的研究更多偏向于解析幾何方向,包括直角坐標系和極坐標系中。
然而,為什么用一個平面截圓錐就能得到橢圓等曲線?這些曲線為什么能滿足解析幾何下的定義?這仍然是困擾許多高中學生的問題。本文以橢圓為例,從平面幾何和立體幾何的角度證明,用平面截圓錐所得曲線確實可以滿足橢圓的解析定義。因直接研究平面截圓錐較煩瑣,本文先從證明平面截圓柱所得“圓柱曲線”為橢圓開始說明。
一、平面截圓柱
首先證明用一個平面截圓柱的側面所得曲線為橢圓,具體可以簡化為如下模型。
例1 如圖1,平面α截圓柱得到曲線C,求證:曲線C為橢圓。
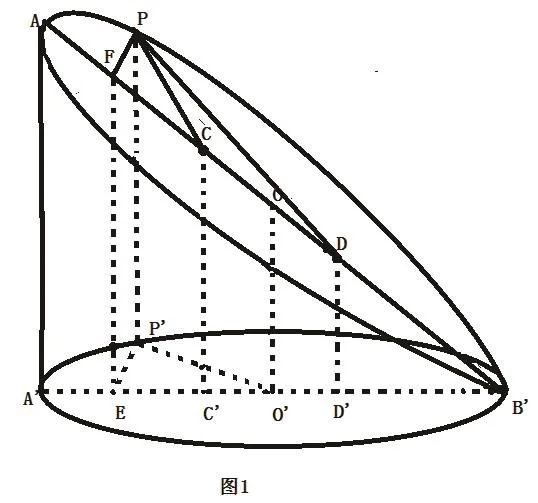
圖1
分析:令A'B'= 2r,AA'= 2h,AB'=2a,則有r2+h2=a2,證明橢圓可以通過其定義“到兩定點的距離之和等于常數”來證明,但關鍵之處就是要確定橢圓的焦點位置,這里可以應用先猜后證的思想。圖中可猜想其“長軸”為2a,“短軸”為2r,則得出其焦距為2h,如果在AB上取兩點C、D,使CO=DO=h,那C、D可能就是兩焦點,這之后如果能證明曲線上任意一點P,使得PC+PD=2a,問題就解決了。
證明:在線段AB上取C、D兩點,使CO=DO=h,做出如圖所示的輔助線,其中PF⊥AB',P'E⊥A'B',易得四邊形PP′EF是矩形。
設P'E=y,EO'=x,則x2+y2=r2,
PC2=PF2+FC2=P'E2+(FE-CC')2+(EO'-C'O')2,

所以曲線C是以2a為長軸,2r為短軸,2h為焦距的橢圓。
這只是證明的第一步,只證明了所謂的“圓柱曲線”為橢圓。如果能證明平面截圓錐側面所得曲線在底面的投影是一個圓,那么運用這個模型就可以直接得出該曲線可以是橢圓的結論,但投影是不是圓有待證明。
二、先猜后證
例2 如圖2,平面α截圓錐形成曲線C,曲線C在圓錐底面的投影是不是圓?
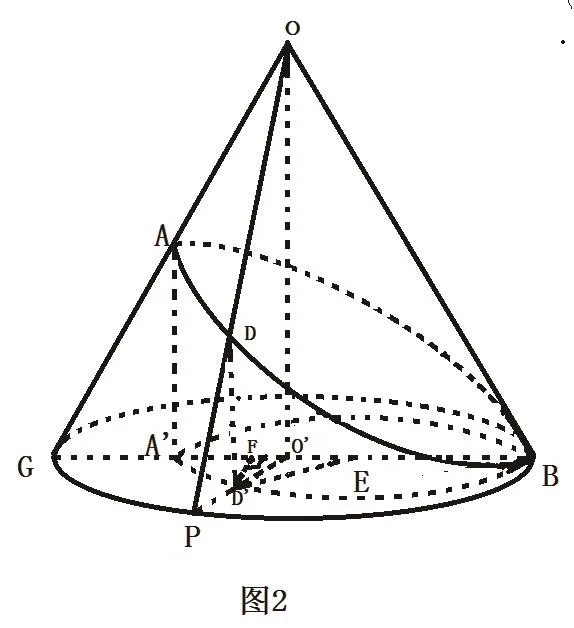
圖2
思路:同樣是先猜后證的思想,猜想它是個圓,之后找等量關系,即其上任意一點到圓心的距離相等。若能證明其是圓,問題便迎刃而解,若不是圓,用字母表示很難證出,最快的方法就是用特殊值法判斷其有沒有可能是圓。
解:用特殊值法判斷。設底面圓半徑R=1,圓錐的高H=3,AA'=2h=2,則h=1,取底面圓上任意一點P,連接PO',PO,PO交曲線C于D,PO'交曲線BA'于D',曲線C的投影是曲線BA',所以DD′與底面垂直。
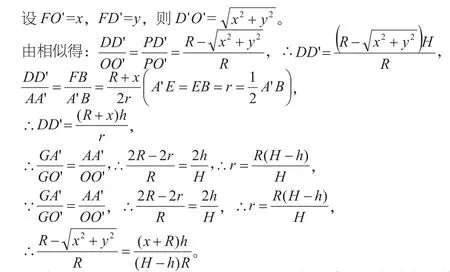
這樣就得到了x,y的關系式,現在只需要將任意一個符合條件的x的值帶入,求出ED'的值,將其與EA'比較,就可初步判斷其是否可能為圓。
∴D'E≠A'E,所以曲線C在圓錐底面的投影不是圓。
這樣便不能運用之前的那個模型,通過此方法也就無法說明曲線C為橢圓,所以這部分只當作先猜后證以及特殊值法的一種運用,激發讀者想到更好的方法。
三、平面截橢圓柱
既然二中的投影不是圓,筆者就自然而然地想到了是橢圓,還是通過一中的方法,首先證明平面截橢圓柱得到的圖形是橢圓。
例3 如圖3,平面α截橢圓柱得到曲線C,求證:曲線C為橢圓。
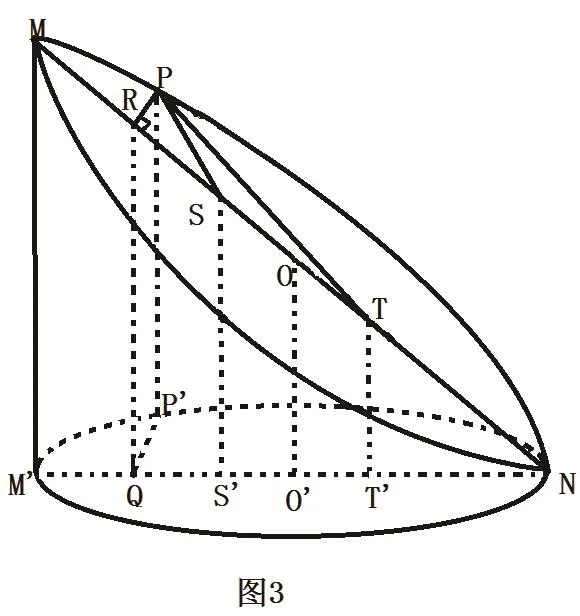
圖3
分析:類似于一中先猜后證的思想方法,先找出其“焦點”位置令NM'=2a,MM'=2h,MN=2A,則有
設底面橢圓的半短軸長(即是曲線C的“半短軸”長)為b,曲線C的半焦距為C,則有同樣的道理,只要在曲線C上找一點P,使得兩“焦點”S、T的距離之和PS+PT=2A,即可得證。
解:設NM'=2a,MM'=2h,MN=2A,底面橢圓的半短軸長為b,則有在M、N上取兩點S、T,使得SO=OT=C(其中

令m=PS+PT,化簡可得:m=2A,所以曲線C為橢圓。
接下來,如果能證明圓錐曲線(橢圓)在底面圓的投影是橢圓,那么運用這個模型就可以解決這個問題了,這里就不再進行深入討論讀者有意可繼續探究。
四、探究過程中發現的結論
回顧“一”中的探究過程,筆者發現了這樣一個現象:
所證橢圓AB的離心率
在三角形BAA'中,sin∠ABA'=仔細觀察發現,該角是平面與圓柱底面所成的二面角,所以可概括為:sinθ=e。(θ為平面截圓柱時,平面與圓柱底面所成二面角的大小,e為所截的橢圓的離心率)
本文是筆者為解開自己和同學們關于圓錐曲線的疑惑所做的研究,證明了橢圓的幾何定義與解析定義的等價性,也發現了一些有益的結論,其中反復運用了先猜后證的思想。猜證思想是數學中重要的工具之一,許多偉大的數學定理都是科學家們先有大致的猜測再經過嚴格的證明得到。同樣,在高中數學解題中,這也是一種很重要的思想,但是在實際操作過程中,同學們往往猜測之后沒有嚴格證明,或者在證明過程中碰到困難就輕易放棄猜想,如在本文二中發現平面截圓錐所得曲線的投影不是圓后,就認為該曲線不是橢圓。這些問題都是同學們常犯的問題,希望本文能為大家對于猜證思想的運用帶來更深的認識,大膽假設,細心求證!

