反比例函數中的面積計算題解析歸類
江蘇省徐州市沛縣楊屯中學 蔡素麗
反比例函數中的面積計算題解析歸類
江蘇省徐州市沛縣楊屯中學 蔡素麗
反比例函數一直是困擾學生的一大難題,特別是和反比例函數相關的面積計算,更讓學生摸不著頭腦。新課程標準對反比例函數這部分的學習目標作了明確的要求:(1)結合具體情境體會反比例函數的意義,能根據已知條件確定反比例函數表達式。(2)能畫出反比例函數圖象,根據圖象和表達式探求k>0和k<0時圖象的變化情況。(3)能用反比例函數解決簡單的實際問題。其中的面積計算是應用中的重中之重。歷數近幾年各地的中考試卷發現,與反比例函數有關的面積計算越來越受出題者的青睞,現結合自己的教學積累,把有關反比例函數面積計算的題目歸類整理如下:
一、數形結合——巧用比例系數k的幾何意義
反比例函數比例系數k與圖形面積之間的關系是現階段初中數學的常見考題類型。k的幾何意義充分體現了學生對于反比例函數問題理解的深度以及本質的把握度。縱觀近幾年考題,此類問題一般以選擇、填空題型出現。現舉例如下:
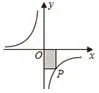
例1 如圖,點P是反比例函數圖象上的一點,過點P分別向x軸、y軸作垂線,若陰影部分面積為12,則這個反比例函數的關系式是__________。
【分析】反比例函數圖象上一點到兩坐標軸之間距離圍成的矩形的面積等于該點橫縱坐標乘積的絕對值,即|xy|,由此可總結得出該矩形面積即為|k|。實際解題中,要結合圖象所在象限,注意k的取值。
【點評】對反比例函數的比例系數k的幾何意義的理解,即過函數圖象上任意一點分別向x軸、y軸作垂線,與坐標軸圍成的矩形的面積是一個定值|k|,理解這一點,解決此類矩形面積問題時將會得心應手。
對于此類k的幾何意義的應用,變式題也是五花八門,變化多樣,但是掌握本質是解題的關鍵,以不變應萬變。
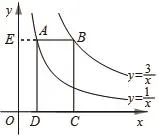
【變式1】如圖,點A在雙曲線y=上,點B在雙曲線y=上,且AB∥x軸,點C和點D在x軸上,若四邊形ABCD為矩形,則矩形ABCD的面積為_______ 。
【分析】初看本題,似乎與k的值無法建立聯系,但是注意觀察可發現,只需延長BA與y軸交于點E,所得兩個矩形,即矩形ADOE、矩形BCOE,兩矩形面積利用對應反比例函數的k的幾何意義即可解決。即S矩形ABCD=S矩形OCBE-S矩形ODAE=3-1=2。
【變式2】如圖,反比例函數y=(x>0)的圖象上,有點P1、P2、P3、P4,它們的橫坐標依次為1、2、3、4。分別過這些點作x軸與y軸的垂線,圖中所構成的陰影部分的面積從左到右依次為S1、S2、S3,則S1+S2+S3= _______。
【分析】由題意可知點P1、P2、P3、P4的坐標分別為:(1,2),(2,1),由平移變換,可把S2、S3平移至左側S1下方,拼成一個矩形,用最左側矩形面積減去下面空白面積即可。由反比例函數的幾何意義可知:

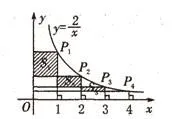
【點評】本題也可以規律題的形式出現,即求S1+S2+S3+…Sn=_______。題目萬變不離其宗,解題的關鍵在于理解k的幾何意義及本質特征。
例2 如圖,點P是反比例函數y=-象上的一點,PD⊥x軸于D。則△POD的面積為_____________。
【分析】解決反比例函數與三角形面積問題也是常見的k的幾何意義的運用。反比例函數圖象上的任意一點向一坐標軸作垂線,與坐標原點連線所構成的直角三角形面積是一個定值實際解題中仍需根據圖象所在象限,注意k的取值。
【變式1】如圖,在平面直角坐標系中,M為y軸正半軸上一點,過點M的直線l∥x軸,l分別與反比例函數的圖象交于A、B兩點,若S△AOB=3,則k的值為______ 。
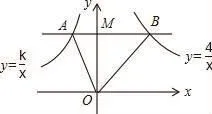
【分析】此題只需兩次利用k的幾何意義與三角形面積之間的關 系 即 可。 即S△AOB=S△AOM+S△MOB=3,S△MOB=故S△AOM=1,所以k=-2。
【變式2】如圖,點A、B在反比例函數的圖象上,過點A、B
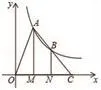
作x軸的垂線,垂足分別為M,N,延長線段AB交x軸于點C,若OM=MN=NC,S△BNC=2,則k的值為( )
A.4 B.6 C.8 D.12
【分析】本題可利用△BOC的三等分點分得的△BNC的面積是△BOC面積的求出△BON的面積為4,利用k的幾何意義求出k=4,故選A。
二、化零為整——妙用反比例函數的對稱性
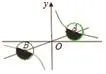
例3 如圖,已知函數y1=k1x與反比例函數y2=的圖象交于A、B兩點(k1>0,k2>0),A點的坐標為(4,2),分別以A、B為圓心的圓與x軸相切,則圖中兩個陰影部分的面積和為_______ 。
【分析】由于反比例函數圖象關于原點成中心對稱,圖中陰影部分的面積和恰好是一個圓的面積,已知兩個圓與x軸相切,所以A點的縱坐標即為圓的半徑。所以S=4π。
【變式】如圖,邊長為8的正方形ABCD的對稱中心是坐標原點O,AB∥x軸,BC∥y軸,反比例函數y=的圖象均與正方形ABCD的邊相交,則圖中的陰影部分的面積之和為_____ 。
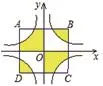
【分析】本題可根據函數表達式,確定兩個函數圖象之間的關系根據正方形的對稱中心是坐標原點,因此,四個小正方形是全等的,反比例函數圖象關于原點成中心對稱,所以陰影部分面積和是兩個小正方形的面積和,故S陰影=×8×8=32。
利用反比例函數的對稱性解題,要結合圖象的特征,合理利用化零為整的思想解決問題。
三、開拓思維——活用設元法
例4 如圖,反比例函數y=(x>0)的圖象經過矩形OABC對角線的交點M,分別與AB、BC交于點D、E,若四邊形ODBE的面積為9,則k的值為_______ 。
【分析】本題可謂逢卷必考,是最受出題者青睞的考題,解決本題可從反比例函數圖象上的點E、M、D入手,分別找出△OCE、△OAD、矩形OABC的面積之間的關系,列出等式求出k值。由矩形的中心對稱性可設M(x,y),則B(2x,2y),解得xy=3,即k=3。
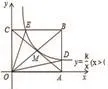
【點評】反比例函數與四邊形的綜合性題目是中考的重要考點,特別是反比例函數結合矩形、正方形的動點問題,更是最近幾年的熱門考點,活用設元法有時會讓人感到豁然開朗,達到事半功倍的效果。
四、抽絲剝繭——智用點的坐標
例 5 已 知A(-4,n)、B(2, -4) 是 反 比 例 函 數
圖象和一次函數y=kx+b的圖象的兩個交點。
(1)求反比例函數和一次函數的解析式;
(2)求△AOB的面積;
(3)直接寫出關于x的不等式kx+b--的解。
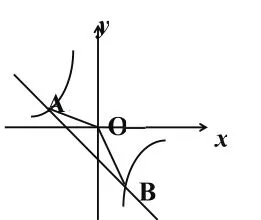
【分析】解決此類題目一般分三步走:(1)利用點的坐標求函數表達式;(2)求交點;(3)求面積。本題由B點坐標代入反比例函數表達式可求出m的值,從而確定反比例函數表達式,進而把A點代入已確定的反比例函數表達式,求出A點坐標,由A、B兩點坐標確定一次函數解析式。求出一次函數與x軸或者y軸的交點坐標,把求△AOB的面積轉化成求△AOC、△COB的面積和。
一次函數美,美在圖象的剛勁、挺拔;反比例函數更美,美在反比例函數圖象優雅、溫柔的獨特氣質。反比例函數蘊含的知識是無窮盡的,值得我們時刻去探討。反比例函數有關面積計算的題目亦是千變萬化,解題方法多樣,深刻理解反比例函數的性質是解題關鍵。

