面向飛機裝配的機器人定位誤差和殘差補償

何曉煦， 田威， 曾遠帆， 廖文和， 向勇

南京航空航天大學 機電學院， 南京 210016

面向飛機裝配的機器人定位誤差和殘差補償

何曉煦， 田威*， 曾遠帆， 廖文和， 向勇

南京航空航天大學 機電學院， 南京 210016

工業機器人由于其高柔性和低成本而被越來越多地應用到飛機自動鉆鉚系統中，使用精度補償有效地提高機器人的絕對定位精度是保證產品質量的關鍵，為進一步提高機器人末端定位精度，提出了基于誤差相似度的殘差補償方法。首先使用基于運動學參數標定的方法辨識出機器人的幾何參數誤差，再利用基于誤差相似度的方法對殘余誤差進行估計，實現對機器人的誤差和殘差的補償。以工業機器人KUKA KR-30 HA為對象所進行的試驗驗證表明，機器人的絕對定位精度平均值由補償前的0.879 mm經過定位誤差補償后提高到0.194 mm，經過殘差補償后進一步提高到0.141 mm，經過定位誤差和殘差補償后的機器人最大誤差由1.492 mm降低為0.296 mm，最大絕對定位精度誤差降低了80.16%。該方法能有效地補償參數辨識后遺留的殘差，進一步提高機器人的定位精度。

飛機裝配； 精度補償； 殘差補償； 最小二乘法； 誤差相似度

工業機器人的飛機自動鉆鉚系統由于能夠有效地提高飛機部件裝配的質量和效率而被越來越廣泛地應用并逐步取代人工作業[1-3]。飛機裝配具有孔位數量多、精度要求高的特點，因此飛機自動鉆鉚系統通常使用離線編程技術對機器人進行鉆孔任務規劃。當機器人采用離線編程進行任務規劃時，通常需要指定末端刀尖點的絕對位置來實現。通常，工業機器人的重復定位精度很高，能夠滿足機器人進行示教編程的精度要求，但其絕對定位精度卻很差。對于沒有標定的機器人，絕對定位精度通常比重復定位精度低1～2個數量級[4]，因此需要通過精度補償提高機器人的絕對定位精度來滿足飛機自動鉆鉚系統中離線編程的精度要求。

現有的提高工業機器人絕對定位精度的方法大體可以分為基于運動學模型的參數標定法[5-7]和非參數標定法。基于運動學模型的參數標定法通常把引起誤差的因素作為各相應變量的微小變化量，通過一系列的參數變量處理建立機器人的運動學模型，并利用測量得到機器人末端定位誤差，經過微分變換等推導出各連桿的實際幾何參數，從而得到修正的機器人運動學模型。但這種基于運動學模型的精度補償方法存在一定的缺陷，因為其通常僅考慮了機器人幾何參數引起的誤差，而幾何參數僅占誤差影響因素的80%～90%[8-10]左右，其余如齒輪間隙、機械臂的質量分布、負載變化、熱效應等非幾何參數引起的誤差無法通過此方法得到補償；且該方法通常需要建立機器人的誤差模型，在動態變化的環境中缺乏柔性[11]。

為克服基于運動學模型的參數標定方法的不足，許多學者提出了很多非運動學參數標定方法，如基于人工神經網絡(Artificial Neural Network, ANN)的標定方法[12-14]和基于誤差相似度的精度補償方法[15-16]等。王東署和付志強[17]把機器人實際位姿和相應的關節角誤差分別作為前饋神經網絡的輸入和輸出來訓練網絡，從而獲得機器人任意位姿時的關節轉角誤差值，通過修改關節轉角值來提高機器人的絕對定位精度。這種標定方法把所有因素引起的誤差均歸結為關節轉角誤差，通過修改關節值來提高機器人的絕對定位精度。Zeng等[15]將機器人及其附屬設備看作一個整體，在此基礎上建立機器人關節輸入和末端位姿的空間相關性模型，將機器人關節轉角作為輸入，可以求得對應的末端位姿誤差，從而實現精度補償，該方法不需要建立機器人運動學模型。

也有一些學者采用將機器人幾何參數誤差和非幾何參數誤差使用不同的方法進行補償以達到補償所有誤差源的效果。Nguyen等[18]使用擴展卡爾曼濾波(Extended Kalman Filter, EKF)算法對機器人幾何參數誤差進行參數辨識，再將參數辨識后的殘差和對應的機器人關節轉角分別作為ANN的輸出和輸入來訓練網絡，從而獲得機器人任意關節轉角時的殘差，然后將經過ANN訓練后得到的機器人末端位姿通過運動學逆解求得修正的關節轉角。

借鑒Zeng等[15-16]提出的基于誤差相似度的機器人精度補償方法，論述了一種基于誤差相似度的機器人殘差補償方法。首先使用迭代的最小二乘法(Levenberg-Marquardt, L-M)[19]辨識出機器人的幾何參數誤差，再利用基于誤差相似度的方法將參數標定后的殘余誤差進行補償。最后使用KUKA KR-30 HA型工業機器人和API-T3激光跟蹤儀對該方法進行試驗驗證，試驗結果表明該方法能進一步提高機器人的絕對定位精度。

1 基于L-M算法的參數標定

1.1 機器人運動學模型

選擇合適的運動學模型對于機器人運動學標定至關重要，其中最常用的是D-H(Denavit-Hartenberg)模型[20]。對于只有旋轉關節的機器人而言，連桿i和i+1之間的關系通過1個旋轉關節變量(關節轉角θi)和3個常量(連桿偏距di、連桿長度ai、扭角αi)來描述。這種方法簡單有效，但也有不足：由于di對相鄰關節軸線平行條件(即αi→0)下的誤差非常敏感，當兩相鄰關節軸線平行(αi→0)時，關節軸姿態的微小變化會使D-H 參數產生巨大的變化(|di|→∞[21])。為避免出現奇異性，使用Veitschegger和Wu[22]提出的修正D-H(Modified D-H, MD-H)模型，即在D-H模型的基礎上附加旋轉參數βi。當相鄰兩關節軸線不平行時，定義di≠0,βi=0；當相鄰兩關節平行時，定義di=0,βi≠0。根據MD-H模型的定義，連桿i-1與i之間的齊次變換矩陣表示為

i-1Ai=Rot(z,θi)·Trans(0,0,di)·

Trans(ai,0,0)·Rot(x,αi)·Rot(y,βi)

(1)

式中：x、y和z分別為連桿坐標系的坐標軸。

對于n個自由度的旋轉關節機器人，其末端法蘭盤相對于基坐標的齊次變換矩陣可以表示為

0Tn=FX(θ)=0A11A2…n-1An

(2)

式中：FX(θ)為名義運動學模型；X為機器人運動學參數組成的向量。

1.2 機器人參數誤差模型

機器人末端位姿誤差是由于各連桿參數存在誤差，通過運動學參數標定的方法使各連桿參數盡可能接近真實值，是基于運動學模型補償的理論基礎。機器人末端法蘭盤中心的實際位置坐標可以表示為

(3)

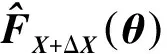
(4)

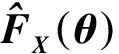
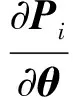
(5)

式中：θ、d、a、α和β由機器人的幾何參數構成；Δθ、Δd、Δa、Δα和Δβ由幾何參數誤差構成。式(5)可寫為

ΔPi=JiΔΧ

(6)

式中：Ji為雅可比矩陣。

在進行運動學參數標定時，通常需要測量一系列采樣點，由式(5)可知，它們的位置誤差可寫為

(7)

式中：m為采樣點個數；ΔP1～ΔPm為點1～m的位置誤差。根據式(5)和式(6)，式(7)可寫為

(8)

式中：ΔP為采樣點的位置誤差向量；J1～Jm為雅可比矩陣。式(8)的求解可以簡化非線性系統問題。

1.3 L-M迭代的最小二乘法

最小二乘法[23]是解決非線性問題最簡單有效的方法之一，具有收斂速度快、計算量小等優點。在此基礎上，研究者提出了很多改進的算法，其中L-M算法[19]應用較為廣泛。L-M算法結合了高斯-牛頓(Gauss-Newton, G-N)算法和最陡下降法的優點，并對二者的不足之處進行了改善，能夠實現快速收斂，并克服逆矩陣不存在或是初始值離局部極小值太遠的情況。根據機器人的理論結構參數對雅克比矩陣和其他參數進行初始化，迭代過程可以分為以下幾步：

1) 計算第k次迭代的機器人雅可比矩陣J(Χk)。

2) 求解第k次迭代的運動學參數誤差改變值，即

ΔΧk=-[JT(Χk)J(Χk)+μkI]-1JT(Χk)ΔP(Xk)

(9)

式中：I為單位矩陣；Χk為第k次迭代時的運動學參數誤差；μk為第k次迭代的阻尼因子；ΔP(Xk)為第k次迭代的位置誤差。

3) 更新第k+1次迭代時的運動學參數誤差為

Χk+1=Χk+ΔΧk

(10)

4) 更新迭代次數為

k=k+1

(11)

5) 更新第k+1次迭代時的阻尼因子為

(12)

將上面計算得到的運動學參數誤差ΔΧ代入機器人運動學正解中，可得到修正的運動學模型下的末端位姿為

T=FX+ΔX(θ)

(13)

式中：FX+ΔX(θ)為修正的機器人運動學模型。

使用L-M迭代的最小二乘法標定出機器人的運動學參數誤差，進而計算出機器人標定后的運動學參數下的機器人末端位姿，可以對機器人進行誤差補償，補償過程在2.4節的精度補償方法中詳細介紹。

2 基于誤差相似度的機器人殘差補償

2.1 殘差的空間相似度

Zeng等[15-16]對工業機器人定位誤差在空間中的分布規律進行了定性和定量分析，利用半變異函數和試驗分析表明工業機器人的定位誤差具有空間相似度，且關節輸入越相近，機器人末端對應的定位誤差越相似。

1.3節中基于L-M迭代的最小二乘法進行的參數標定僅對機器人幾何參數誤差引起的末端位置誤差進行補償，該誤差矢量在笛卡爾坐標系下的各個分量是由機器人各連桿運動學參數組成的一系列三角函數來描述的。對于旋轉關節機器人而言，只有各關節轉角為變量，其他參數及參數誤差均為常量，因此在機器人各關節可達范圍內，由三角函數描述的幾何誤差量是連續可微的。所以當機器人各關節輸入越相近時，對應的由參數標定法補償的位置誤差存在相似度。

由以上分析可知，機器人定位誤差和由1.3節的參數標定法補償的定位誤差都具有相似度，那么機器人經過參數標定后的殘差也具有相似度。機器人末端位置殘差與關節轉角一一對應，在一組關節輸入θi對應的末端位置殘差ΔP(θi)和與之相近的一組關節輸入θj對應的末端位置殘差ΔP(θj)之間具有某種程度的自相關，這種相關性與θi和θj之間的距離hi,j有關，定義hi,j為兩關節轉角向量在機器人關節空間中的歐幾里得距離，即

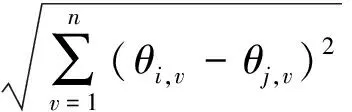
(14)

式中：v為機器人第v個連桿；θi,v和θj,v分別為第i和j個點的連桿v的關節轉角。

當兩關節轉角向量在機器人關節空間中的歐幾里得距離hi,j越小時，代表這兩個關節轉角向量之間的相似度越強。當hi,j→0時，可以認為：機器人在某一關節位置θi的末端殘余誤差ΔP(θi)偏大或者偏小時，與之相近的某處關節轉角θj，即與該關節位置θi的歐幾里得距離hi,j→0的關節轉角θj對應的末端殘余誤差ΔP(θj)也偏大或者偏小。

2.2 基于誤差相似度的殘差建模

利用機器人經過參數標定后的殘余誤差具有空間相似度的性質，可以解決機器人殘余誤差補償的問題。由采樣點的殘余誤差建立一個基于空間相似度的描述機器人殘余誤差分布規律的模型，由這個模型可得到目標點殘差和每個采樣點殘差之間的空間相似度，然后用線性無偏最優估計的方法計算出目標點的殘余誤差。因此，目標點的殘差可以根據估計的殘差通過修改機器人的位置命令補償。即在待補償區域內建立采樣點的理論位置Ps與參數標定后的位置殘差ΔPsr之間的空間相似度模型，從而估算出目標點Pt的殘差ΔPtr，進行殘差補償。

由以上分析可知，需首先利用采樣點的殘余誤差建立一個描述機器人殘余誤差分布規律的空間相似度模型。根據泰勒公式，殘余誤差與關節轉角的關系可以表示為一個線性函數和一個非線性函數相加，且利用回歸分析可以研究目標點殘差關于機器人關節轉角的具體依賴性，因此將采樣點殘差與機器人關節轉角的關系近似表達為一個回歸模型和一個隨機過程疊加。基于誤差相似度的殘余誤差估計模型的建立過程如下。

在自由度為n的機器人待標定區間內隨機選擇m個采樣點，關節轉角向量表示為

(15)

式中：θs1～θsm為采樣點1～m的關節轉角向量。

任一采樣點k的關節輸入為

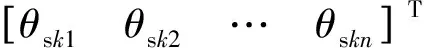
(16)

式中：θsk∈Θs；θsk1～θskn為采樣點k的連桿1～n關節轉角。

用一個回歸模型和一個隨機過程將機器人采樣點k在l方向的殘余誤差表示為

ΔPsrk,l(θsk)=W(c:,l,θsk)+gl(θsk)l=x,y,z

(17)

式中：l為笛卡兒坐標系的x、y、z方向；gl(θsk)為隨機過程，平均值為0；c:,l為回歸參數向量；W(c:,l,θsk)為關于θsk的回歸模型，展開為

W(c:,l,θsk)=c1,l+c2,lθsk1+…+cn+1,lθskn=

(18)

式中：c1,l～cn+1,l為需要擬合的回歸參數；f(θsk)為關于關節轉角的函數。

可以構造所有采樣點關于關節轉角的向量，即

(19)

式中：f(θs1)～f(θsm)為采樣點1～m關于關節轉角的函數。

任意兩個采樣點關節輸入θsi和θsj(θsi,θsj∈Θs)的隨機過程gl(θsi)和gl(θsj)之間的協方差為

(20)

(21)

式中：ξv為連桿v的模型參數，且ξv∈ξ；θsi,v和θsj,v分別為第i和j個采樣點的連桿v的關節轉角。

將所有采樣點殘余誤差之間的相似度模型表示為R，則任意兩點殘余誤差之間的相似度模型為

Ri,j=S(ξ,θsi,θsj)

(22)

式中：Ri,j為矩陣R的第(i,j)個元素。式(22)中ξ可以由最大似然估計求得，即

(23)

式中：|R|為R的行列式。

根據式(22)，將式(20)寫為

(24)

采用最小二乘法對參數向量c:,l進行最小二乘估計，為書寫方便，下文將c:,l寫為c，即

(FTF)c*=FTΔPsr

(25)

式中：c*為c的最小二乘估計。

當

(26)

且

E[gl(θsi)gl(θsj)]=0i≠j

(27)

則R為一個對角線矩陣，即

(28)

引入權重矩陣Q，即

(29)

將式(25)中的F和ΔPsr分別替換成QF和QΔPsr，則權重值方程可寫為

(FTQ2F)c*=FTQ2ΔPsr

(30)

參數c的廣義的最小二乘解為

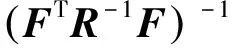
(31)

求解出參數ξ和c，基于誤差相似度的機器人殘余誤差補償模型就建立完成。

2.3 基于誤差相似度的殘差估計

對目標點的殘差估計過程如下。建立某一目標點的關節輸入θti，該目標點與采樣點之間的相關度模型r表示為

r(θ)=

[S(ξ,θs1,θti)S(ξ,θs2,θti) …S(ξ,θsm,θti)]T

(32)

式中：S(ξ,θs1,θti)～S(ξ,θsm,θti)分別為目標點與采樣點1～m的相似度模型。

可以通過建立目標點與采樣點在l方向的殘差之間的線性關系，得到目標點在l方向上的估計殘差為

(33)

式中：w為所有采樣點權重，是一個m×1的列向量；ΔPsr,l為采樣點在l方向的殘差組成的m×1的列向量；則wTΔPsr,l為標量。

求出最優的采樣點的權重w是得到目標點殘差的關鍵，最優解應滿足與目標點空間相似度越大所占的比重就越大的要求。目標點殘余誤差估計的偏差為

wT(Fc+G)-(fTc+gl(θti))=

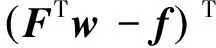
(34)

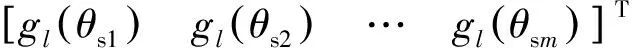
FTw-f=0orFTw=f

(35)

在這個條件下，可以求得目標點的均方誤差(Mean Squared Error, MSE)為

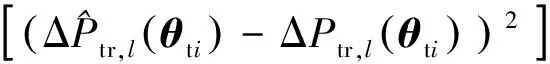
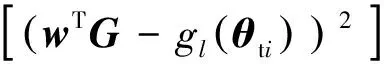
(36)

式中：r為目標點關于各采樣點的誤差相似度模型。為了獲得目標點的位置殘差，需要計算出使φ(θti)最小化的權值w，這個問題可以轉化為條件極值問題，即

subject toFTw=f

(37)

該問題可以由拉格朗日乘數法解決，式(37)的拉格朗日方程為

(38)

式中：λ為拉格朗日乘子。將式(38)對w求導得

(39)

令式(39)為0，得

(40)

由式(40)求解出權值w代入式(33)即可求得目標點的殘差，進而進行殘差補償。

2.4 精度補償方法

基于誤差相似度的殘差建模流程如圖1所示。在待補償區域內隨機選取m個采樣點Ps:

1) 將Ps經過以下過程處理得到參數標定后的殘差ΔPsr。

步驟1將采樣點理論位置Ps輸入機器人，用激光跟蹤儀測量出機器人補償前的末端位置Psm，則補償前機器人的末端位置誤差ΔPm=Psm-Ps。

步驟2將采樣點Ps和對應的位置誤差ΔPm代入1.3節中計算得到修正的運動學模型下機器人的末端位置Pke。

步驟3將補償量PL輸入機器人，用激光跟蹤儀測量得到機器人末端位置PLm，可以由ΔPsr=PLm-PL得到誤差補償后的殘余誤差ΔPsr。

以上過程中出現的誤差和補償量對比如下。ΔPm∶ΔPm=Psm-Ps，表示機器人補償前的位置誤差；ΔPke∶ΔPke=Pke-Ps，表示在修正的運動學模型下預測的機器人末端位置誤差；PL∶PL=Ps-ΔPke，表示誤差補償時輸入給機器人的補償量，即經過參數標定后輸入給機器人的值；ΔPsr∶ΔPsr=PLm-PL，表示機器人參數標定后的位置誤差。

圖1 采樣點殘差建模流程圖
Fig.1 Flowchart of residual error modeling of sample point

2) 將采樣點Ps和對應的經過誤差補償后的末端位置殘差ΔPsr代入2.2節中的殘差估計建模方法中建立殘差估計模型。

在完成基于誤差相似度的殘差建模以后，在機器人運動空間可達范圍內的q個目標點Pt可以通過圖2進行誤差和殘差的補償：

1) 計算目標點Pt對應的殘差ΔPtr：根據2.3節基于誤差相似度的殘余誤差估計方法，將Pt、Ps和ΔPsr輸入已經建好的基于誤差相似度的殘差估計模型中，得到ΔPtr，ΔPtr為目標點經過誤差補償后的殘余誤差。

2) 計算目標點基于L-M法預測的運動學參數下的機器人末端位置誤差ΔPf：

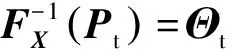
步驟2將Θt代入修正的運動學模型中求得機器人末端預測位置Pf。

步驟3由ΔPf=Pf-Pt得到在修正的運動學模型下預測的機器人末端位置誤差ΔPf。

3) 由Pp=Pt-ΔPf-ΔPtr得到補償量Pp，即目標點經過誤差和殘差補償后，輸入給機器人的補償量。

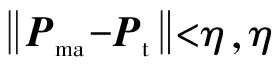
至此，目標點誤差和殘差補償完成。

圖2 目標點定位誤差和殘差補償流程圖
Fig.2 Flowchart of positioning error and residual error compensation of target

3 試驗驗證和數據分析

3.1 試驗設計及機器人坐標系建立

試驗以KUKA KR-30 HA六自由度工業機器人為載體，使用API-T3激光跟蹤儀測量機器人末端位置(圖3)。

將激光跟蹤儀靶球(Spherically Mounted Reflector, SMR)安放在機器人末端執行器上(圖4)，由于在測量過程中，安裝在機器人法蘭盤上的末端執行器與法蘭盤之間的相對位置是不變的，所以激光跟蹤儀靶球測出的位置可以看做TCP的位置。

圖3 工業機器人與激光跟蹤儀
Fig.3 Industrial robot and laser tracker

圖4 末端執行器上的靶球
Fig.4 SMR on end effector

采樣點和目標點都是相對于機器人坐標系的，激光跟蹤儀測量出來的數據也相對于機器人基坐標系。如圖5所示，建立機器人基坐標系具體過程如下：

步驟1保持A2～A6軸不動，轉動A1軸，使用激光跟蹤儀測量得到一組點，將這些點擬合成圓O1，O1的軸線即為基坐標系的z軸。

步驟2按步驟1的方法轉動A2軸，使用激光跟蹤儀測量得到一組點，將這些點擬合成圓O2。

步驟4按步驟1的方法轉動A4軸，使用激光跟蹤儀測量得到一組點，將這些點擬合成圓O3，將圓O3的圓心向機器人基座平面投影，該投影點為機器人坐標系x軸上的一點。

步驟5使用以上步驟得到的3個特征(坐標原點、x軸上的點和z軸)建立機器人坐標系。

按照坐標的平移與變換建立每個關節軸的坐標系(圖6)。機器人名義運動學參數如表1所示。

圖5 基坐標系的建立方法
Fig.5 Method of building base frame

圖6 KUKA KR-30 HA機器人運動學模型
Fig.6 Kinematic model of a KUKA KR-30 HA robot

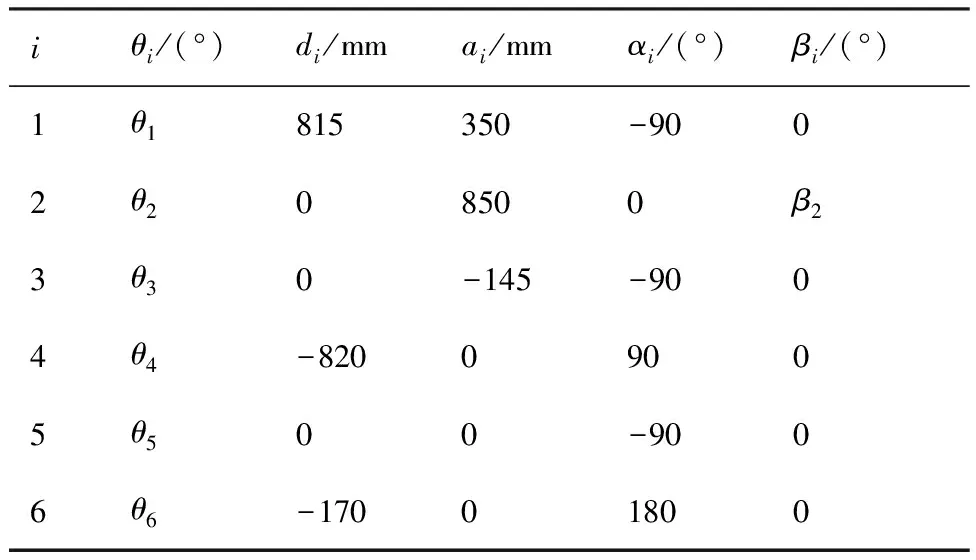
表1 KUKA KR-30 HA機器人名義運動學參數

3.2 試驗結果

本試驗在機器人運動范圍內的500 mm×800 mm×650 mm的立方體空間中且機器人末端位置轉角A、B、C∈[-15°,15°]區域內隨機生成100個采樣點和197個目標點。

將100個采樣點使用1.3節中迭代的最小二乘法，辨識出機器人運動學參數誤差，如表2所示。再將100個采樣點經過圖1的方法建立基于誤差相似度的殘差補償模型，用197個目標點經過2.4節中圖2的方法驗證殘差補償方法的有效性。

用激光跟蹤儀分別測量目標點補償前、定位誤差補償后和殘差補償后的位置誤差。利用x、y、z三個方向的位置誤差Δx、Δy、Δz計算得到機器人的絕對定位精度為

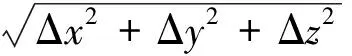
(41)

將測量的目標點的絕對定位精度作出折線圖如圖7所示，絕對定位誤差的頻數直方圖如圖8所示，分別放大圖7(a)、圖8(a)得到圖7(b)、圖8(b)。

197個目標點由補償前最大誤差為1.492 mm，平均值為0.879 mm，經過基于L-M法的定位誤差補償后，最大誤差降為0.321 mm，平均值降為0.194 mm。補償效果明顯，機器人定位精度得到大幅度提高，且波動范圍很小，基于L-M法補償后的機器人絕對定位精度均在0.35 mm內。

197個目標點用基于誤差相似度的殘差補償方法進行殘差補償后，最大誤差降為0.296 mm，平均值降為0.141 mm，最大誤差有所減小，平均值明顯降低，殘差補償后絕對定位精度均在0.3 mm 內。相比較于只使用基于L-M法補償的機器人絕對定位精度有了進一步提升。為了更直觀地顯示試驗結果，將試驗數據統計如表3所示。可以看出，經過誤差和殘差補償后的機器人最大絕對定位誤差降低了80.16%。應用基于運動學模型的參數標定法結合基于誤差相似度的殘差補償方法補償效果優于只用參數標定的方法。

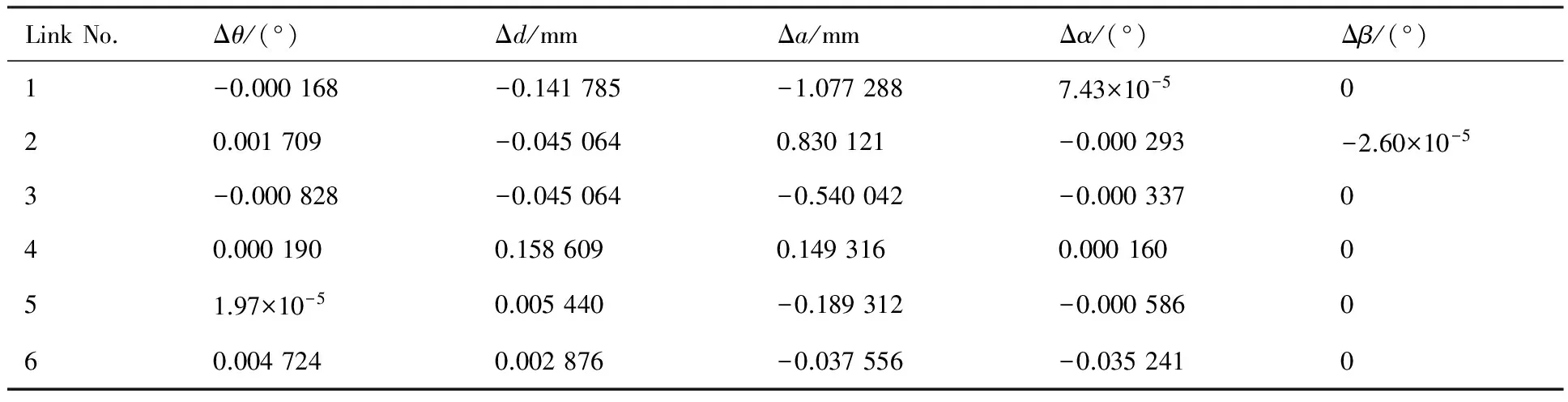
表2 KUKA KR-30 HA機器人辨識的運動學誤差Table 2 Identified kinematic errors of a KUKA KR-30 HA robot

圖7 絕對定位誤差折線圖
Fig.7 Line charts of absolute positioning error

圖8 絕對定位精度頻數直方圖
Fig.8 Histogram of frequency of absolute positioning accuracy

表3 試驗數據統計Table 3 Statistical data of test

4 結 論

1) 使用參數標定方法僅對機器人幾何參數誤差進行補償，經過參數標定后仍遺留殘差，故有必要對殘差進行補償。

2) 機器人末端位置經過參數標定后的殘差具有空間相似度，利用采樣點的位置和其對應的基于L-M法補償后的末端位置殘差建立殘差估計模型，可以估計任意目標點對應的殘差，對殘差進行補償。

3) 通過KUKA機器人和激光跟蹤儀進行試驗驗證，試驗結果表明，基于誤差相似度的殘差補償方法效果優于僅使用參數標定的方法，能夠有效地進一步提高機器人絕對定位精度。

4) 基于參數標定和誤差相似度的殘差補償將機器人絕對定位精度的平均值提高到0.141 mm，最大誤差降低為0.296 mm，對于提高機器人絕對定位精度效果良好，適用于飛機鉆鉚系統等對機器人精度要求較高的場合。

5) 在構建末端位置殘差與機器人關節轉角之間的關系時，采用了一個回歸模型和一個隨機誤差表示，對于機器人奇異位姿的情況沒有做考慮，因此對于機器人奇異位姿的情況還有待進一步研究。

[1] DEVLIEG R, SITTON K, FEIKERT E, et al. ONCE (ONe-sided Cell End effector) robotic drilling system: SAE Technical Paper-2002-01-2626[R]. New York: SAE International, 2002.

[2] TIAN W, ZHOU Z, LIAO W. Analysis and investigation of a rivet feeding tube in an aircraft automatic drilling and riveting system[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(5-8): 973-983.

[3] ZHAN Q, WANG X. Hand-eye calibration and positioning for a robot drilling system[J]. The International Journal of Advanced Manufacturing Technology, 2012, 61(5-8): 691-701.

[4] 彭商賢, 方浩天, 張平. 裝配機器人高精度定位補償系統[J]. 機器人, 1992, 14(3): 11-16, 23.

PENG S X, FANG H T, ZHANG P. High precision system with positioning compensation for assembly robot[J]. Robot, 1992, 14(3): 11-16, 23 (in Chinese).

[5] VEITSCHEGGER W K, WU C H. Robot calibration and compensation[J]. IEEE Journal on Robotics and Automation, 1988, 4(6): 643-656.

[6] ZAK G, BENHABIB B, FENTON R G, et al. Application of the weighted least squares parameter estimation method to the robot calibration[J]. Journal of Mechanical Design, 1994, 116(3): 890-893.

[7] PARK I W, LEE B J, CHO S H, et al. Laser-based kinematic calibration of robot manipulator using differential kinematics[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(6): 1059-1067.

[8] DENNIS J E, SCHNABEL R B. Numerical methods for unconstrained optimization and nonlinear equations[M]. New Jersey: Prentice-Hall, 1983: 64-65.

[9] JUDD R P, KNASINSKI A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE Transactions on Robotics and Automation, 1990, 6(1): 20-30.

[10] RENDERS J M, ROSSIGNOL E, BECQUET M, et al. Kinematic calibration and geometrical parameter identification for robots[J]. IEEE Transactions on Robotics and Automation, 1991, 7(6): 721-732.

[11] ELATTA A Y, GEN L P, ZHI F L, et al. An overview of robot calibration[J]. Information Technology Journal, 2004, 3(1): 74-78.

[12] ZHONG X, LEWIS J, N-NAGY F L. Inverse robot calibration using artificial neural networks[J]. Engineering Applications of Artificial Intelligence, 1996, 9(1): 83-93.

[13] ZHUANG H, ROTH Z S, HAMANO F. Optimal design of robot accuracy compensators[J]. IEEE Transactions on Robotics and Automation, 1993, 9(6): 854-857.

[14] ZHUANG H, ROTH Z S. Method for kinematic calibration of Stewart platforms[J]. Journal of Robotic Systems, 1993, 10(3): 391-405.

[15] ZENG Y F, TIAN W, LI D W, et al. An error-similarity-based robot positional accuracy improvement method for a robotic drilling and riveting system[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(9-12): 1-11.

[16] ZENG Y F, TIAN W, LIAO W H. Positional error similarity analysis for error compensation of industrial robots[J]. Robotics and Computer-Integrated Manufacturing, 2016, 42: 113-120.

[17] 王東署, 付志強. 機器人逆標定方法研究[J]. 計算機應用, 2007, 27(1): 71-73.

WANG D S, FU Z Q. Study on robot inverse calibration[J]. Computer Applications, 2007, 27(1): 71-73 (in Chinese).

[18] NGUYEN H N, ZHOU J, KANG H J. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network[J]. Neurocomputing, 2015, 151(3): 996-1005.

[19] GINANI L S, MOTTA J M S T. Theoretical and practical aspects of robot calibration with experimental verification[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2011, 33(1): 15-21.

[20] LIN P D, TSAI J. The machining and on-line measurement of spatial cams on four-axis machine tools[J]. International Journal of Machine Tools and Manufacture, 1996, 36(1): 89-101.

[21] BARKER L K. Modified Denavit-Hartenberg parameters for better location of joint axis systems in robot arms: NASA-TP-2585[R]. Washington, D.C.: NASA, 1986.

[22] VEITSCHEGGER W, WU C H. Robot accuracy analysis based on kinematics[J]. IEEE Journal on Robotics and Automation, 1986, 2(3): 171-179.

[23] ZAK G, BENHABIB B, FENTON R G, et al. Application of the weighted least squares parameter estimation method to the robot calibration[J]. Journal of Mechanical Design, 1994, 116(3): 890-893.

Robotpositioningerrorandresidualerrorcompensationforaircraftassembly

HEXiaoxu,TIANWei*,ZENGYuanfan,LIAOWenhe,XIANGYong

CollegeofMechanicalandElectronicalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Nowadays,industrialrobotshavebeenincreasinglyappliedtoaircraftautomaticdrillingandrivetingsystemduetotheirhighflexibilityandlowcost.Thekeytoproductqualityassuranceiscompensatingtheabsolutepositionalerrorsoftheroboteffectively.Inordertofurtherimproveendlocationaccuracyoftherobot,amethodofcompensationforresidualerrorbasedonerrorsimilarityisproposed.Thegeometricparametersoftherobotarefirstidentifiedbasedonkinematicsparametercalibration.Theresidualerroristhencompensatedbasedonerrorsimilarity.AnexperimentontheKUKAKR-30HAindustrialrobotisconductedtodemonstratetheeffectivenessofthecompensation.Theresultshowsthattheaverageabsolutepositioningaccuracyoftherobotcanbeimprovedfrom0.879mmto0.194mmaftercompensationofthepositioningerror.Theaverageabsolutepositioningaccuracyisfurtherincreasedto0.141mmafteraresidualcompensation.Themaximumabsolutepositioningerrorisreducedby80.16%from1.492mmto0.296mm.Thismethodcancompensatetheresidualerrorsleftoverafterparameteridentificationeffectively.

aircraftassembly;precisioncompensation;residualerrorcompensation;leastsquaremethod;errorsimilarity

2016-06-17；Revised2016-07-18；Accepted2016-08-12；Publishedonline2016-10-191314

URL：www.cnki.net/kcms/detail/11.1929.V.20161019.1314.006.html

s：NationalNaturalScienceFoundationofChina(51475225,51575273);NationalHigh-gradeCNCMachineToolsandBasicManufacturingEquipment(2014ZX04001071)

2016-06-17；退修日期2016-07-18；錄用日期2016-08-12； < class="emphasis_bold">網絡出版時間

時間：2016-10-191314

www.cnki.net/kcms/detail/11.1929.V.20161019.1314.006.html

國家自然科學基金 (51475225,51575273)； 國家高檔數控機床與基礎制造裝備 (2014ZX04001071)

＊

.E-mailtw_nj@nuaa.edu.cn

何曉煦， 田威， 曾遠帆， 等． 面向飛機裝配的機器人定位誤差和殘差補償J． 航空學報,2017,38(4):420538.HEXX,TIANW,ZENGYF,etal.RobotpositioningerrorandresidualerrorcompensationforaircraftassemblyJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):420538.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0235

V262.4; TP242.2

A

1000-6893(2017)04-420538-11

(責任編輯： 李世秋)

＊Correspondingauthor.E-mailtw_nj@nuaa.edu.cn