分布式協同動態任務規劃的建模與一體化求解方法

崔乃剛，吳蔚楠，郭繼峰

（哈爾濱工業大學 航天學院，哈爾濱 150001）

分布式協同動態任務規劃的建模與一體化求解方法

崔乃剛，吳蔚楠，郭繼峰

（哈爾濱工業大學 航天學院，哈爾濱 150001）

以多異構無人機執行偵查、打擊、評估任務為背景，開展了協同任務規劃問題建模、一體化求解算法設計。采用分布式規劃框架及圖論思想對問題進行建模，且將無人機避碰、燃油、任務執行次序作為約束條件，并充分考慮任務分配與路徑規劃存在的強耦合特性，采用禁忌/遺傳算法，設計包含任務序列和路徑位姿點的基因編碼，將問題進行一體化求解。結果表明：算法能夠適用于動態任務場景，且能夠較為快速地解決任務空間較為復雜的規劃問題。

異構無人機；一體化求解；協同任務規劃；分布式決策；Dubins路徑；禁忌/遺傳混合算法

無人飛行器（后文均用 UAV表述）越來越多地被用來執行各種自主任務[1]，而這些任務的成功與否依賴于UAV的自主程度。根據Kendou[2]提出的無人飛行系統自主等級可知，當前相對成熟的是 UAV本體的自主控制、單機自主避障與路徑規劃等自主等級較低的技術，為了適應更為復雜的任務需求，需要采用多機協同替代單機執行任務，而協同任務規劃技術是協同控制領域的關鍵技術。

協同任務規劃問題是一個典型的組合優化問題，文獻[3-8]均證明其為 NP（Non-deterministic polynomial）完全問題，故其求解難度較大。為了降低求解難度，通常將協同任務規劃問題簡化為協同任務分配和路徑規劃兩個子問題，弱化或不考慮它們之間的耦合性，采用分層解耦的方法對它們進行分別求解[3,7,10-14]。這些解法的共同點為：將任務分配和路徑規劃分別求解，在任務分配求解時不考慮對象本身的運動學約束、環境障礙、威脅區約束，僅考慮任務本身的時序約束，任務間的相互影響關系等；路徑規劃將任務分配的結果作為其輸入，尋找滿足 UAV自身約束、障礙、威脅區、避碰等約束的平滑航跡。分層解耦方式降低了問題的求解難度，且能夠適用于任務空間態勢確定的離線任務規劃問題。但是，實際的任務空間態勢通常是時變且不確定的，而分層解耦方法的解算過程是異步的，由于任務分配過程的時間消耗，其運算結果并非響應當前的任務空間態勢，從而帶來的路徑規劃結果往往不能滿足實際任務需求，且極有可能造成任務失效。所以，分層解耦求解方法的應用范圍有限，且不能滿足實際任務需求。

基于此，文獻[5,15-18]對任務規劃問題的一體化求解算法進行了研究。A. Richards[15]采用歐幾里德線段集表示 UAV的路徑規劃結果，通過建立混合整數線性規劃模型完成對協同任務規劃問題的等效，最后采用一體化求解方法完成問題求解；Rasmussen[16]采用圖論等效方法完成任務規劃模型建立，并通過圖搜索算法完成對相同 UAV協同任務規劃問題的求解；Shima[5]采用集中式一體化任務規劃求解方法，通過圖論方法完成 UAV協同任務規劃問題的等效，采用Dubins路徑表示UAV飛行路徑，最后通過遺傳算法完成問題求解；Deng[17]在文獻[5]的基礎上，附加考慮了 UAV的彈藥數量約束，通過改變遺傳算法的基因編碼方式，完成了問題的求解。以上文獻均是基于集中式架構完成協同任務規劃問題的建模與求解，將規劃運算過程完全在地面站或某個 UAV上完成，而集中式架構普遍存在對通信鏈路依賴性較強、可靠性較差等缺點[7]，所以其實用性較差。Edison[18]提出了采用分布式一體化策略求解協同任務規劃問題的思路，但是其并未實現。由協同任務規劃一體化求解方法的研究現狀可知，現有方法主要存在以下不足：

1）采用集中式架構，可靠性及規劃更新速度較慢；

2）能夠適應的任務場景較為簡單；

3）考慮到的約束條件較少，不能反映真實任務場景。

鑒于現有的協同任務規劃方法存在的普遍問題，基于文獻[5][15-17]的研究成果，以異構 UAV協同執行偵查確定、打擊、評估任務為背景，基于分布式規劃策略，通過圖論思想將協同任務規劃問題進行描述，在考慮 UAV轉彎半徑約束、特性（包括載荷特性、巡航速度）約束、任務執行時序性約束、偵查范圍約束、避碰約束等前提下，采用一體化求解方法，設計禁忌/遺傳算法，完成協同任務規劃問題求解。

1 協同任務規劃問題建模

1.1 參數定義

以UAV協同執行偵查、打擊、評估任務為背景，首先對涉及到的相關參數進行定義。

目標集與任務集：

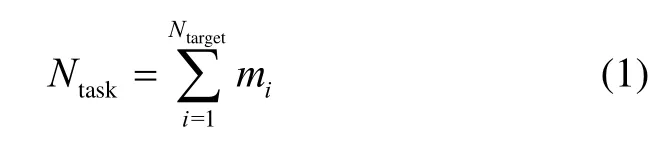
UAV的異構性主要體現在兩個方面：1）UAV的可執行的任務不一致；2）UAV的速度和極限轉彎半徑不一致。UAV可分為三類：1）作戰UAV：可執行所有任務，用偵查UAV：可執行偵查和評估任務，用彈藥 UAV：僅能執行打擊透明目標任務，用

1.2 問題的數學描述

在給定一個包含Ntask個子任務的任務集和Nuav個可分配 UAV的情況下，任務規劃的目標為：在滿足任務自身約束和外部約束條件的前提下，尋求一種最優的分配方案，使系統的效用最大。該問題包含連續的規劃路徑以及離散的決策變量，是一個典型的組合優化問題。

不失一般性，任務規劃問題可描述如下：

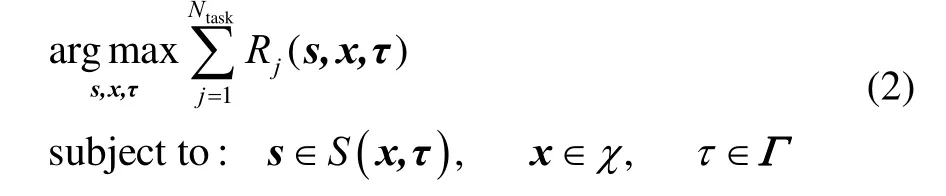
由式(2)可知，任務規劃的可行解集由S×χ×Γ決定，但是由于協同任務存在多UAV多目標、UAV異構、UAV燃油約束、UAV避碰、任務間存在時間序列約束等因素，將會極大地增加問題解集的勢，對問題的求解帶來較大的難度。

1.3 問題的簡化

本文采用圖論的思想，將任務規劃問題用有向圖形式等效描述[5]，完成對問題的適當簡化，并基于分布式規劃架構，將任務決策和路徑規劃過程分布到各UAV上，完成對問題的分布式描述。

通過離散UAV在目標處的進入航向角（UAV航向角定義參見圖1），完成對任務規劃問題的簡化，再通過圖論思想將任務空間表述為有向圖。

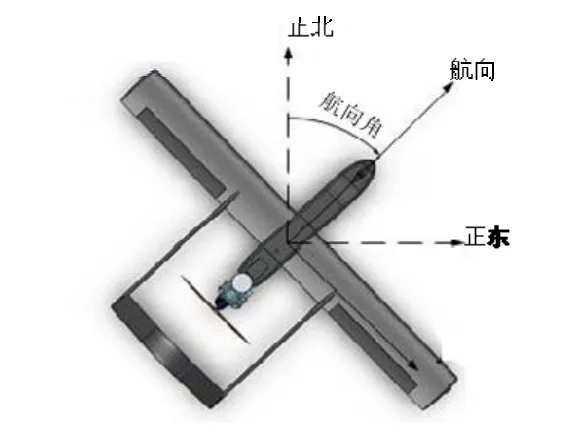
圖1 UAV的航向角定義Fig.1 Definition of UAV orientation angle

離散后的航向角可表示如下：

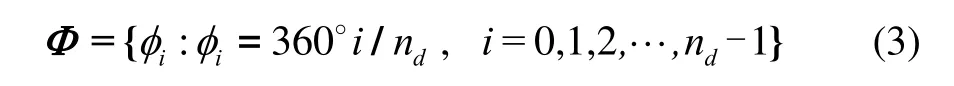
式中：nd表示航向角的離散化程度，nd取值越大，離散化程度越高；iφ表示UAV在目標處的航向角。

根據圖論的思想，有向圖由頂點V和有向邊E組成。協同任務規劃問題的有向圖頂點可表示如下：

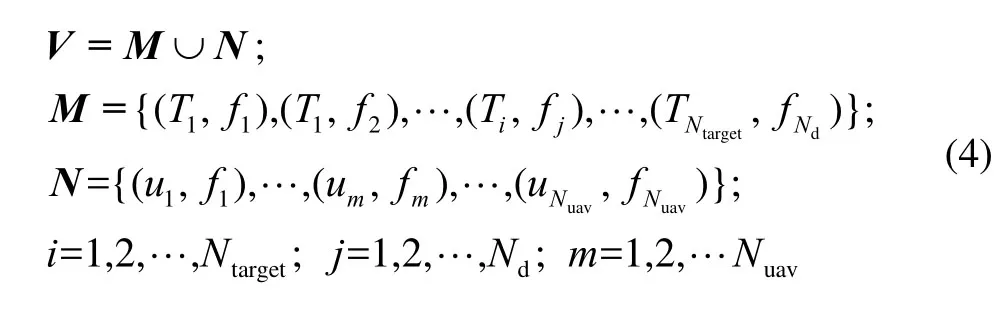
式中：M表示包含離散化后的所有任務位姿點的集合；N表示包含所有UAV初始位姿點的集合；V為M與N的并集，表示有向圖的所有頂點集合，

有向圖的邊E為M中各頂點間的有向連線、 N中各UAV初始位姿點與M中的目標點的有向連線的并集。

下面通過實例說明離散簡化過程，設置偵查(Search)、打擊(Attack)、評估(Verify)任務場景如下：

2) 目標為2個：Ntarget=2，且每個目標處對應的任務數量為 3，均包括偵查(S)、打擊(A)、評估(V)三項任務，即

有：

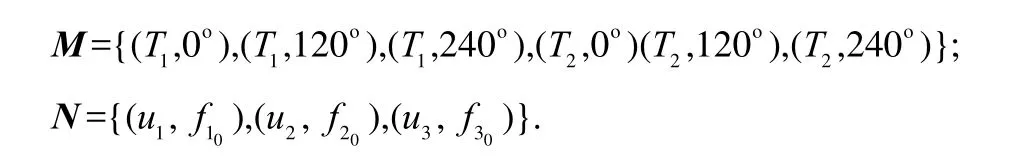
圖2為該任務場景對應的有向圖。

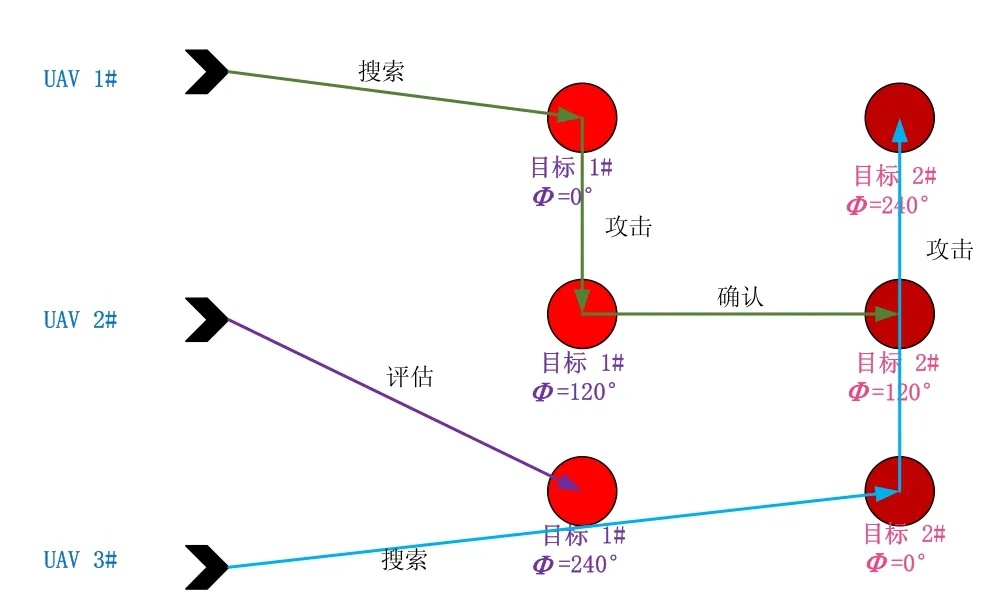
圖2 協同任務規劃問題的有向圖例圖Fig.2 Example diagram of the SAV task planning by graph theory

由圖 2可知，圖中的有向邊路徑表示 UAV1、UAV2、UAV3的任務次序與飛行路徑：綠線表示UAV1首先搜索目標1并對其進行攻擊，最后再飛向目標2處完成對目標2的毀傷效果評估；紫線表示UAV2對目標1進行毀傷效果評估；藍線表示UAV3首先對目標2進行搜索，然后對目標2進行攻擊。

上述有向圖對應任務規劃的一個可行解，其解集可表示為S為所有飛行路徑的解集，由圖2可知，其解集包括6條飛行路徑，每一條路徑的長度對應兩個位姿點間的 Dubins路徑，路徑總長度為所有 Dubins路徑長度之和。

χ代表任務分配的決策變量集，由圖2可知：

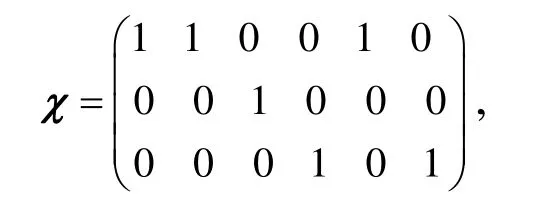
式中，ijχ表示第i個UAV與第j個任務的匹配結果。

Γ代表規劃結果中各任務的執行時間戳，僅需滿足偵查、打擊、評估任務的執行次序即可。

由上述分析可知，可將 UAV的總飛行距離作為協同任務規劃問題的指標，則該問題的效用函數可簡化為如下形式：

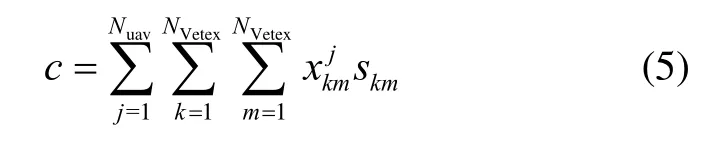
式中：c為系統的效用值；為有向圖中頂點集V的基數，即頂點的個數；為取值為0或1的決策變量，表示第j架UAV是否選擇有向圖中第k個頂點與第m個頂點連線對應的Dubins路徑作為其飛行路徑；skm為對應該UAV選擇的Dubins路徑的長度。

將式(5)進行分布式處理，分布到各 UAV上進行獨立求解，即：

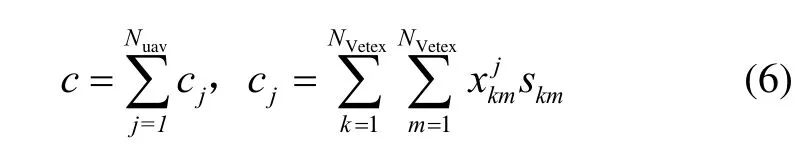
式(6)為式(5)的分布式形式，可將單個cj的運算分布到每個UAV完成獨立解算。

為了反映較為真實的任務空間，還需要滿足如下5項約束：

1）任務完成約束：UAV需要執行完所有規定的任務，可表示為：

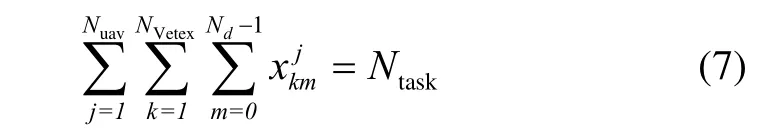
2）任務時序約束：對于某一目標，其偵查、打擊、評估三項任務間需滿足如下約束條件：

即該目標需要先進行偵查才能進行攻擊，且被攻擊后才能進行毀傷評估。

3）載荷約束：只有裝有相應任務載荷的UAV才能執行對應的任務，即只有作戰 UAV才能執行所有三項任務，偵查 UAV只能執行偵查和評估任務，彈藥類UAV只能執行攻擊任務。

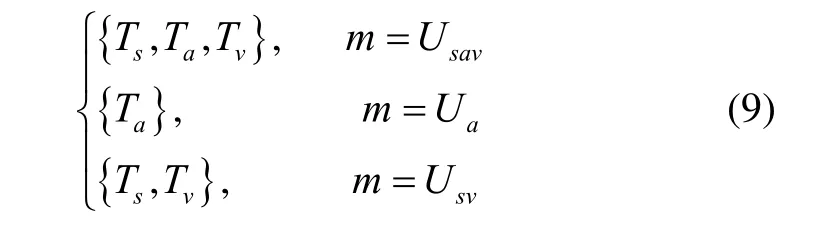
4）避碰約束：主要考慮多UAV間的避碰約束，采用不相交路徑法[8]，即UAV的路徑存在相交點，當且僅當UAV同時到達相交點時，才會發生碰撞，給出避碰約束如下。

令sp,sq分別表示UAVp和UAVq的Dubins路徑，若sp與sq存在相交點?，則需要滿足：

式中：d?,p,q表示相交點處路徑sp,?與sq,?的長度之差；分別表示 UAV的安全圓半徑；分別表示UAV在路徑sp,?、sq,?的平均飛行速度。

5）燃油約束：

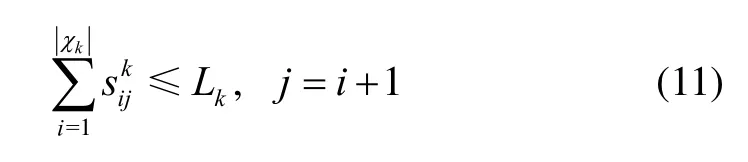
式中，kχ表示第k個UAV的任務分配決策矩陣，Lk為第k個UAV可飛行的總路徑長度。

由目標函數式(5)(6)和約束條件(7)～(11)完成描述了異構UAV的分布式協同任務規劃問題。

最后給出UAV的運動學模型，將其等效為Dubins Car模型。

給出如下假設：

1）戰場環境是事先已知的，且戰場環境的態勢信息獲取是瞬間完成且準確的；

2）僅考慮二維平面內的規劃問題；

3）各UAV之間的通信鏈路是可靠且信息一致的，且數據傳輸是瞬間完成的；

4）UAV的巡航速度為恒定的。

Dubins Car等效建模的思想主要來自于Dubins得出的證明結論：兩個位姿點間的最短路徑是 Dubins路徑[9]，

Dubins Car模型適合于描述有轉彎半徑約束的UAV狀態，故建立UAV運動學方程如下：

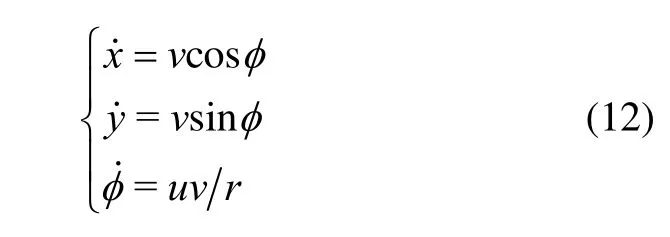
將遺傳算法作為求解上述混合整數優化問題的主算法，基于分布式架構[19]，采用一體化求解方法，重新設計遺傳算法的基因編碼方式，由任務分配信息和路徑規劃信息組成染色體，最后加入禁忌搜索思想，對遺傳算法進行改進，完成問題的求解。

式中：x,y為笛卡爾慣性坐標系下的水平分量；v為UAV巡航速度；φ為UAV速度方向與x方向的夾角，稱為UAV航向角，且規定順時針方向為正，參見圖2；r為UAV的極限轉彎半徑，r越大，其機動能力越差；u為UAV的控制輸入量，易知，

2 禁忌/遺傳算法及算法評估準則

2.1 禁忌/遺傳混合算法的基本步驟

禁忌/遺傳混合算法的主體是遺傳算法，只是將禁忌搜索算法的思想引入遺傳算法中，對遺傳算法中的交叉或者變異操作進行一定的改進，提高遺傳算法的搜索速度，避免遺傳算法的“早熟”現象。

禁忌/遺傳混合算法的基本步驟如圖3所示。

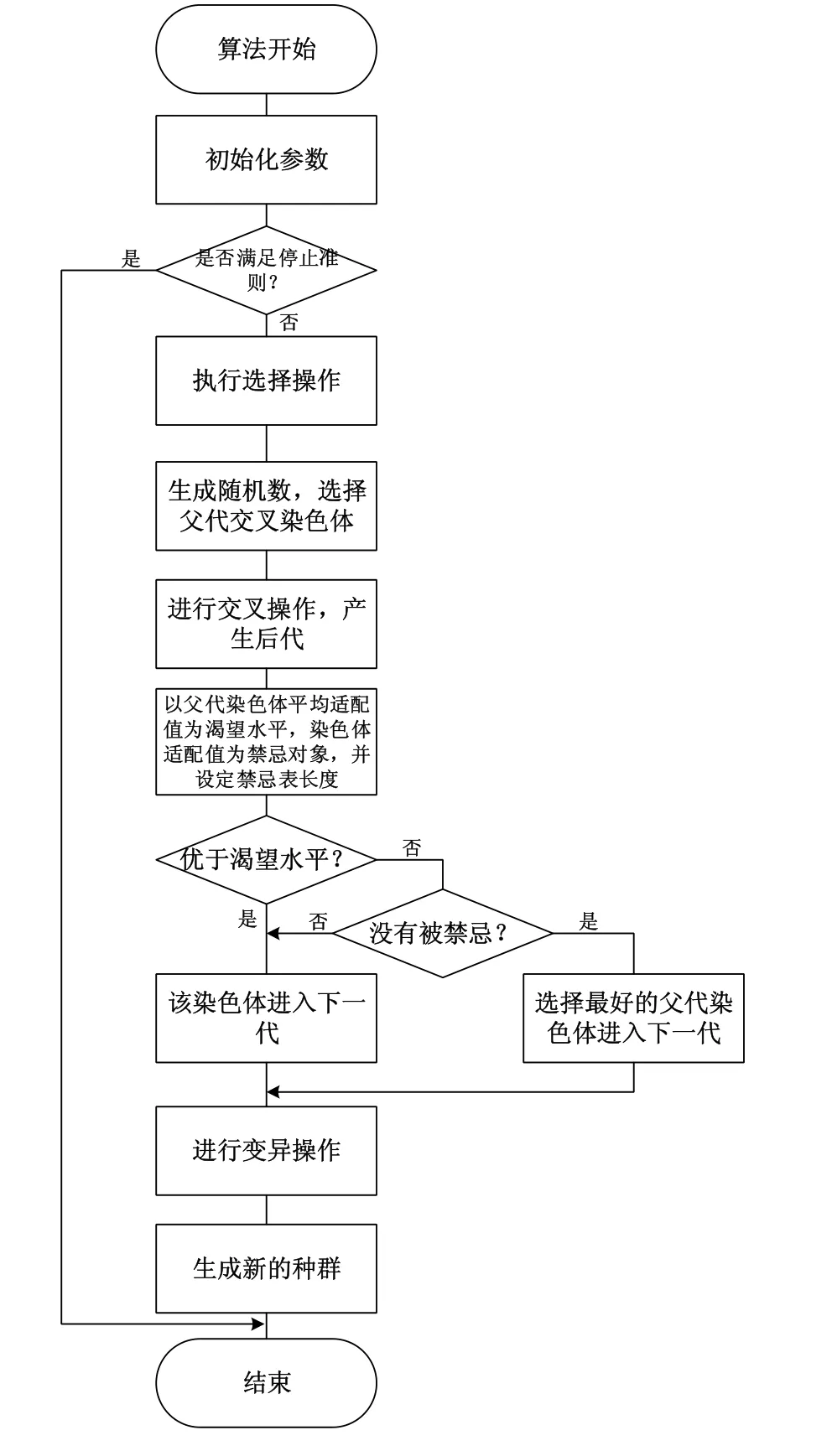
圖3 禁忌/遺傳混合算法的基本步驟Fig.3 Flow diagram of the tabu/genetic hybrid search algorithm

2.2 算法評估準則

算法的定量分析主要包括三個方面：

1）算法品質

算法品質定義為如下形式：

式中：Jbase表示所有參與評估的算法得出的解對應的最小航跡長度；表示某算法得出的解對應的航跡長度；quality表示該算法對應的算法品質。

由式(13)可知，算法品質可用于量化描述某算法相比于其他算法的性能優劣。算法品質可與蒙特卡洛法配合使用，當算法運行的次數為N時，其算法的品質得分為：

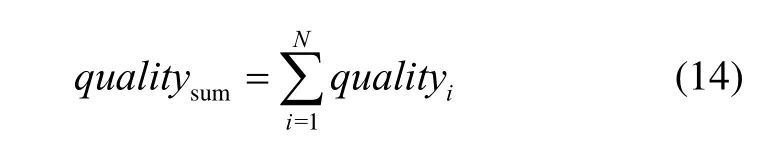
2）算法運行速度品質

3）算法品質與運行時間的加權

算法的優劣不能單一的通過運行時間和算法品質進行評估。通過設定權值，從算法品質和運行時間兩方面評估算法的優劣：

3 仿真驗證與分析

算法測試環境為Interval Zero RTX64實時操作系統。

任務空間場景基本參數如表1所示。

表1 任務空間設置Tab.1 Setting of task scenes

1）任務場景1

任務空間參數設置如表1所示，UAV的安全圓半徑均為50 m，每架UAV可飛行的總路徑長度為10 km。

分配結果如表2所示。

表2 算法運行分配結果Tab.2 Allocation result of the algorithm

算法運行結果對應的Dubins路徑如圖4所示。

記錄算法在RTX64環境下的運行時間為21.92 s。

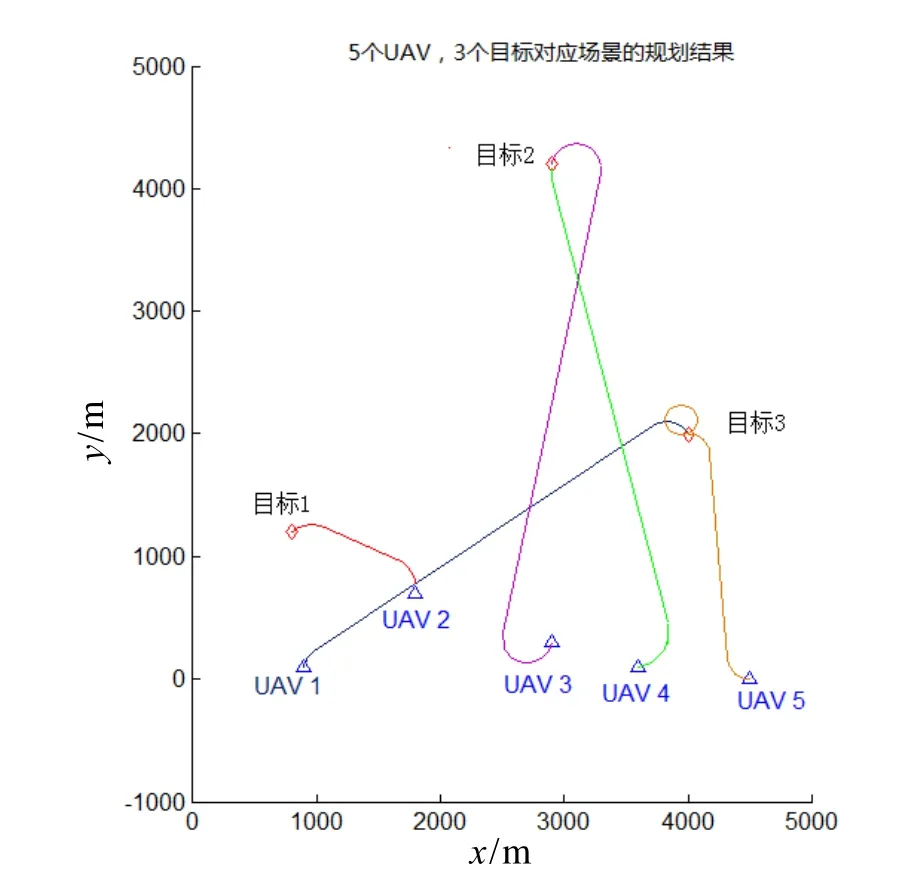
圖4 UAV規劃結果對應的Dubins路徑Fig.4 Dubins trajectory of scenario with 3 targets and 5 UAVs

2）任務場景2

其他參數不變，考慮目標位置發生變化的情況。設Target 1和Target 2在仿真開始后10s開始機動：Target 1向笛卡爾坐標系X軸正向移動1700 m，向Y軸機動400 m；Target 2向Y軸移動800 m，且機動過程瞬間完成。

算法得到的分配結果與表2中相同，得到的更新Dubins路徑如圖5所示。

由圖5的仿真結果可知，由于目標機動，UAV2、UAV3、UAV4的Dubins路徑均發生變化，算法完成了對動態環境的響應，記錄算法運算時間為26.41 s。

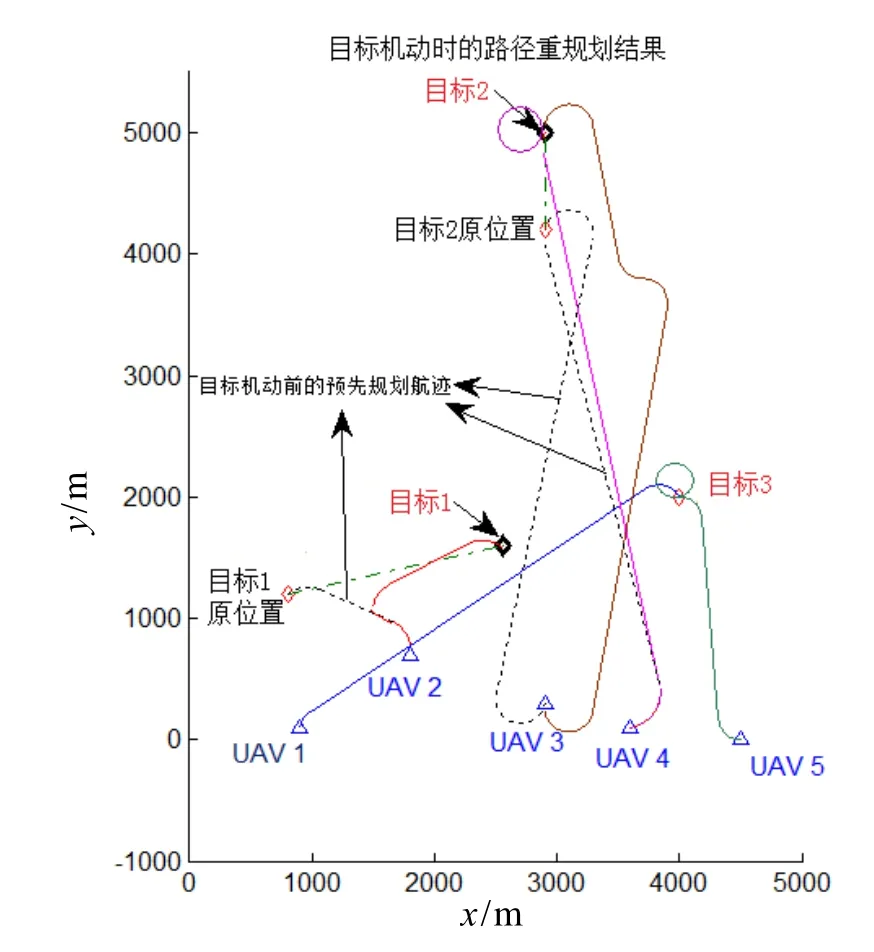
圖5 目標機動時的重規劃結果對應的Dubins路徑Fig.5 Dubins trajectory of scenario with moving targets

3）任務場景3

任務場景3的參數設置如表1所示，設置任務空間在 20 km×20 km范圍內，UAV的極限轉彎半徑為UAV的速度大小為v∈[60 m/s,80 m/s]，禁忌/遺傳算法的基本參數設置如表3所示。

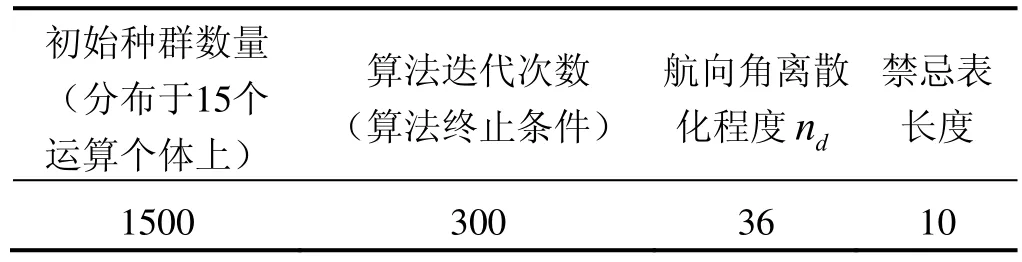
表3 禁忌/遺傳混合算法參數設置Tab.3 Parameters setting on tabu/genetic hybrid algorithm

采用蒙特卡洛分析方法，設置實驗次數為100，用于對比分布式一體化求解方法與優化工具CLPEX、典型分布式分層解耦求解算法[12]的性能，令 ==0.5 α β ；記錄算法運行的時間和算法得出的總路徑長度，如表4所示。

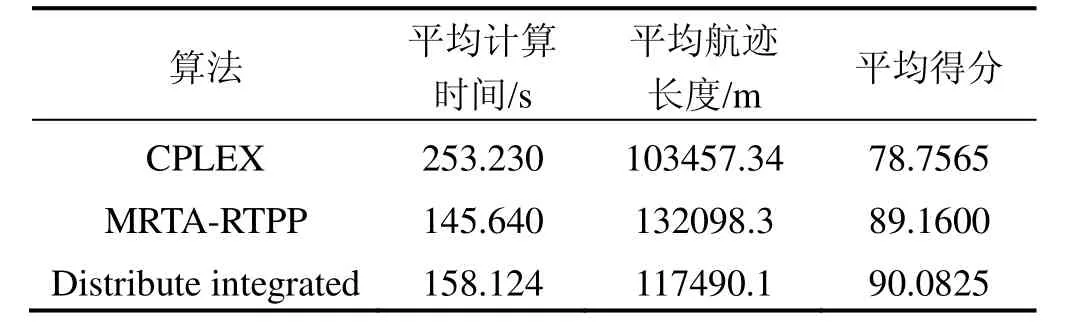
表4 各算法運行結果Tab.4 Results of three algorithms

各算法的運行時間對比結果如圖6所示。

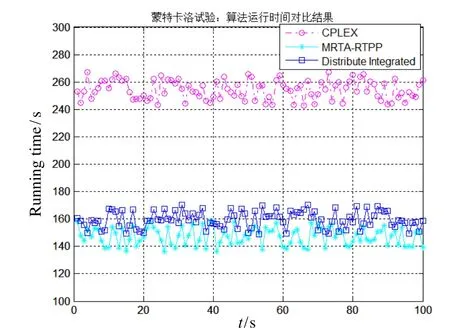
圖6 基于蒙特卡洛試驗的各算法運行時間對比結果Fig.6 Running time results of three algorithms based on Monte Carlo test

根據上述結果可知，相比CPLEX，雖然分布式一體化解法得出的解對應的總路徑長度略大，但分布式一體化解法的平均運算時間縮短約90s，綜合兩項算法評估標準，分布式一體化解法性能更好；相比MRTA-RTPP[12]，分布式一體化解法得出的解更逼近最優解，但MRTA-RTPP[12]方法的運算速度更快，其平均運算時間比分布式一體化解法快約5 s，其運算時間優勢并不明顯，綜合兩項評估標準，分布式一體化解法性能更優。

4 結 論

1）相比于分層解耦求解方法，一體化求解方法更接近最優解；分布式規劃框架將問題的求解分散到各 UAV實體上，可有效提高算法的求解速度。實驗證明，在任務空間存在一定動態性的情況下，基于分布式架構的一體化求解算法具有較好的實時性，可以完成任務的快速響應，具有一定的實用價值，且算法對比實驗在實時系統 RTX上進行，運行環境相對穩定，對比結果具有說服力。

2）在考慮UAV避碰、UAV燃油、UAV任務載荷、UAV異構、任務執行次序等約束條件下，結合Dubins Car模型可實現UAV飛行航跡與UAV動力學模型的等效轉換，基于圖論思想，通過 UAV的飛行航向角的離散化完成對協同任務規劃這一NP問題的離散簡化，可以實現對協同任務規劃問題的等效建模。通過與針對混合整數線性規劃的優化算法包 CPLEX的仿真對比，證明建模方法具有一定的有效性和實用性。

3）由于未考慮UAV間的通信延遲、UAV的飛行航跡的高度維，且假設偵查類UAV完成偵查任務是瞬間完成的，故現有工作存在不足，且一體化求解算法不能適用于任務空間更為復雜（參與任務的實體數大于20）的情況，求解過程需要考慮“死鎖”情況，所以建模方法與算法仍需進一步改善；同時，經初步分析可知，UAV飛行航向角的離散程度的nd越大，算法求解時間亦會增加，但是帶來的解的最優度并不能顯著提高，所以離散量nd的取值也是后續研究的關鍵內容。

（References）：

[1]Maza I, Caballero F, Capitan J, et al. Experimental results in multi-UAV coordination for disaster management and civil security applications[J]. Journal of intelligent &robotic systems, 2011, 61(1): 563-585.

[2]Kendou F. Survey of advances in guidance, navigation,and control of unmanned rotorcraft systems[J]. Journal of Field Robotics, 2012, 29(2): 315-378.

[3]Rathinam S, Sengupta R, Darbha S. A resource allocation algorithm for multivehicle systems with nonholonomic constraints[J]. IEEE Trans. Autom. Sci. Eng.,2007, 4(1): 98-104.

[4]Savla K, Frazzoli E, Bullo F. On the point-to-point and traveling salesperson problems for Dubins’ vehicle[C]//American Control Conference. June 2005: 786-791.

[5]Edison E, Shima T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms[J]. Computers and Operations Research, 2010, 38(1): 340-356.

[6]Cons M S, Shima T, Domshlak C. Integrating task and motion planning for unmanned aerial vehicles[J]. Unmanned Systems, 2014, 2(1): 19-38.

[7]Ponda S S, Johnson L B, Geramifard A, et al. Cooperative mission planning for multi-UAV teams[M]. Handbook of Unmanned Aerial Vehicles. Springer Netherlands,2015: 1447-1490.

[8]Chandler P R, Pachter M, Swaroop D, et al. Complexity in UAV cooperative control[C]//American Control Conference. IEEE, 2002, Vol.3: 1831-1836.

[9]Dubins L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79(3): 497-516.

[10]沈林成, 陳璟, 王楠. 飛行器任務規劃技術綜述[J]. 航空學報, 2014, 35(3): 593-606.Shen Lin-cheng, Chen Jing, Wang Nan. Survey on task planning technology for aircraft[J]. Acta Aeronautica Et Astronautica Sinica, 2014, 35(3): 593-606.

[11]Tsourdos A, White B, Shanmugavel M. Cooperative path planning of unmanned aerial vehicles[M]. John Wiley &Sons, 2010.

[12]Woosley B, Dasgupta P. Multi-robot task allocation with real-time path planning[C]//Proc. of the Twenty-Sixth International Florida Artificial Intelligence Research Society Conference. 2013: 574-579.

[13]Arsie A, Savla K, Frazzoli E. Efficient routing algorithms for multiple vehicles with no explicit communications[J].IEEE Transactions on Automatic Control, 2009, 54(10):2302-2317.

[14]Moon S, Oh E, Shim D H. Integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments[J]. Journal of Intelligent & Robotic Systems, 2013, 70(1-4): 303-313.

[15]Richards A, Bellingham J, Tillerson M, et al. Coordination and control of multiple UAVs[C]//AIAA Guidance,Navigation, and Control Conference. Monterey, CA. 2002.

[16]Rasmussen S J, Shima T. Tree search algorithm for assigning cooperating UAVs to multiple tasks[J]. International Journal of Robust and Nonlinear Control, 2008,18(2): 135-153.

[17]Deng Q B, Yu J Q, Wang N F. Cooperative task assignment of multiple heterogeneous unmanned aerial vehicles using a modified genetic algorithm with multi-type genes[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1238-1250.

[18]Edison E. Task assignment and path optimization for cooperating uninhabited aerial vehicles[D]. Technion Israel Institute of Technology, Faculty of Aerospace Engineering, 2009.

[19]Pospichal P, Jaros J, Schwarz J. Parallel genetic algorithm on the cuda architecture[M]. Applications of Evolutionary Computation. Springer Berlin Heidelberg, 2010: 442-451.

[20]黃榮, 崔乃剛, 韋常柱, 等. 基于 RRT-GPM 兩階策略的導彈編隊協同突防最優軌跡快速設計[J]. 中國慣性技術學報, 2015, 23(3): 356-362.Huang Rong, Cui Nai-gang, Wei Chang-zhu, et al. Rapid trajectory optimization for cooperative penetration of missile formation based on two-stage RRT-GMP strategy[J]. Journal of Chinese Inertial Technology, 2015, 23(3):356-362.

[21]鄭重, 熊朝華, 黨宏濤, 等. 時變通信延遲下的無人機編隊魯棒自適應控制[J]. 中國慣性技術學報, 2016,24(1): 108-113.Zheng Zhong, Xiong Zhao-hua, Dang Hong-tao, et al.Robust adaptive control for unmanned aerial vehicle’s formation with time-varying communication delays[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 108-113.

Integrated distributed method for dynamic cooperative mission planning problem

CUI Nai-gang, WU Wei-nan, GUO Ji-feng
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Based on multi-heterogeneous UAVs in dynamic mission scenario of reconnaissance, striking and verifying, this paper establishes the models for cooperative mission planning problem, and designs an integrated distributed algorithm. Because of the disadvantages of the centralized planning framework, this paper adopts distributed planning framework. First, the graph theory is employed to transform the mission planning problem into directed graph under the constraint conditions of collision avoiding, fuel consuming,and the mission sequence. The Dubins Car Model is used to stand for the UAV’s kinematic model. Then,without decoupling the planning solution problems, this paper designs an integrated planning framework, and adopts the genetic/tabu search hybrid algorithm to solve the planning problem. At Last, some examples was presented in several simulation scenarios to compare the performance and computational results from different algorithms, which show that the integrated distributed method can be applied to the dynamic mission scenario, and can rapidly solve the planning problem with complex missions.

heterogeneous UAVs; integrated method; cooperative mission planning; distributed decisionmaking; Dubins path; tabu/genetic hybrid algorithm

1005-6734(2017)04-0523-07

10.13695/j.cnki.12-1222/o3.2017.04.018

TP29

A

2017-04-08；

2017-07-20

國家自然科學基金（11472090）

崔乃剛（1965—），男，教授，博士生導師，主要飛行器總體設計、制導控制、任務規劃領域研究。E-mail: Cui_Naigang@163.com