圖像復(fù)原技術(shù)在低劑量CT圖像去噪中的應(yīng)用

李正定

圖像復(fù)原技術(shù)在低劑量CT圖像去噪中的應(yīng)用

李正定

目的探討大規(guī)模圖像并行復(fù)原技術(shù)在低劑量CT圖像快速去噪中的應(yīng)用。方法基于圖像復(fù)原的變分PDE模型，針對(duì)大規(guī)模圖像復(fù)原問題，結(jié)合非精確Newton法和區(qū)域分解技術(shù)，構(gòu)造模型的Newton-Krylov-Schwarz（NKS）并行求解算法，利用該方法對(duì)低劑量CT的低對(duì)比分辨力圖像進(jìn)行處理分析。結(jié)果針對(duì)大規(guī)模灰度圖像，數(shù)值算例顯示，該方法具有很好的收斂性、穩(wěn)定性和并行可擴(kuò)展性，處理后的低劑量CT的低分辨力圖像明顯優(yōu)于未處理的圖像。結(jié)論（1）本文提出的算法圖像處理效果基本達(dá)到了一般圖像處理算法的精度；（2）本文的算法比現(xiàn)有的圖像處理算法的速度要快；（3）本文提出的算法可以處理大規(guī)模的圖像。

ROF模型；低劑量CT；區(qū)域分解算法

1 引言

目前大力倡導(dǎo)低劑量CT，低劑量的成像會(huì)導(dǎo)致噪聲增加，為了能夠清晰地分辨出病變的位置，需要對(duì)這些原始的圖像進(jìn)行去噪處理，使其更加清晰。圖像濾波是圖像復(fù)原的傳統(tǒng)方法，由于邊緣部分集中了圖像的大部分信息，因此要求圖像濾波在去除圖像的模糊和噪聲的同時(shí)，又要保持圖像的細(xì)節(jié)。近年來發(fā)展起來的變分偏微分方程（PDE）圖像復(fù)原技術(shù)，在去噪的同時(shí)能夠很好的保持圖像的邊緣，受到研究者的廣泛關(guān)注。

本文擬研究求解ROF[1]（Rudin-Osher-Fatemi）模型及其改進(jìn)模型的基于區(qū)域分解算法的并行Newton-Krylov-Schwarz（NKS）算法。精確Newton法對(duì)小規(guī)模問題比較有效，但當(dāng)問題規(guī)模巨大時(shí)，其對(duì)應(yīng)的線性化方程組很難精確求解，這時(shí)非精確Newton算法[2]成為首選，其使用迭代算法非精確求解線性化方程組，獲得近似的Newton方向。NKS算法將問題由尋找相對(duì)于Jacobian矩陣的一個(gè)高效預(yù)處理算子，轉(zhuǎn)變?yōu)閷ふ蚁鄬?duì)于線性向前算子的一個(gè)好的預(yù)處理算子。算法的核心在于用Schwarz[3]預(yù)條件子加上Krylov[4]子空間校正法求解相應(yīng)的Jacobian系統(tǒng)：它既能夠大幅減少Jacobian矩陣的條件數(shù)，又易于大規(guī)模并行可擴(kuò)展性計(jì)算。伴隨著并行計(jì)算機(jī)計(jì)算性能的日益提高，由于Schwarz 預(yù)條件子具有優(yōu)良的并行結(jié)構(gòu)，許多科研工作者致力于研究這類算法求解工程計(jì)算中的大規(guī)模線性或非線性問題。蔡小川教授在經(jīng)典Schwarz 預(yù)條件子的基礎(chǔ)上提出了一類限制Schwarz 預(yù)條件子和兩水平預(yù)條件子，并將其成功應(yīng)用于流體優(yōu)化控制[5]，人體動(dòng)脈血液模擬問題[6]等。文獻(xiàn)[7-8]從理論上證實(shí)了上述預(yù)條件子的優(yōu)越性。

2 Newton-Krylov-Schwarz（NKS）算法

給定噪聲圖像為初值μ0，用精確Newton法求解此模型，由于方程組病態(tài)，高度非線性，并且規(guī)模巨大，直接求解十分困難。運(yùn)用迭代法求解該模型，每步迭代過程中都涉及到整個(gè)圖像區(qū)域的像素點(diǎn)的計(jì)算，計(jì)算量巨大，對(duì)于大規(guī)模的圖像，串行求解其基于該模型的復(fù)原問題幾乎是不可能的。對(duì)于FP方法和Newton法，均需要求解一個(gè)線性系統(tǒng)，并且當(dāng)問題規(guī)模較大時(shí)，80%的計(jì)算時(shí)間耗費(fèi)在對(duì)該線性系統(tǒng)的求解。并且當(dāng)正則化參數(shù)β較小時(shí)，該線性系統(tǒng)的條件數(shù)很大，因此，需要采用預(yù)處理技術(shù)以加快收斂速度。為更好的利用現(xiàn)有的超級(jí)計(jì)算機(jī)平臺(tái)，充分發(fā)揮其超級(jí)計(jì)算性能，我們采用結(jié)合了區(qū)域分解技術(shù)，非精確Newton法以及Schwarz預(yù)處理技術(shù)的NKS算法，將該大規(guī)模問題轉(zhuǎn)化為一系列小規(guī)模的子問題，分別在單個(gè)處理器上進(jìn)行求解。

3 數(shù)值算例

將通過2D灰度圖像復(fù)原的數(shù)值模擬實(shí)驗(yàn)來驗(yàn)證NKS算法的收斂性、有效性和穩(wěn)定性，并且測(cè)試其并行可擴(kuò)展性。據(jù)我們了解，目前，NKS算法尚未應(yīng)用到圖像復(fù)原領(lǐng)域。因此，驗(yàn)證該算法的有效性和并行可擴(kuò)展性具有重要的理論和應(yīng)用價(jià)值。

3.1 CT圖像去噪

這一節(jié)利用本文提出的算法對(duì)一些真實(shí)的醫(yī)學(xué)圖像進(jìn)行去噪處理，圖像來源于浙江大學(xué)醫(yī)學(xué)院附屬第一醫(yī)院的一臺(tái)西門子CT上用CT性能模體（CATPHAN 500）掃描得到。該模塊主要是用來測(cè)試CT的低分辨力。掃描所用的條件電壓都是80 kV，層厚都是10 mm，毫安數(shù)從67 mA到533 mA，毫安數(shù)越低，噪聲越大。圖1為本文算法獲得的去噪結(jié)果。

3.2 NKS算法并行可擴(kuò)展性

對(duì)規(guī)模不同的兩幅灰度圖像，在不同處理器核數(shù)下，NKS算法的并行可擴(kuò)展性結(jié)果，Newton迭代步數(shù)及平均每個(gè)Newton步中GMRES迭代步數(shù)的比較如表1所示。當(dāng)處理器個(gè)數(shù)增加的時(shí)候，Newton迭代步數(shù)基本不變，平均GMRES迭代步數(shù)略有增加，計(jì)算時(shí)間迅速減小。超線性并行可擴(kuò)展性是指當(dāng)使用的處理器數(shù)目增加一倍時(shí)，所用的總的計(jì)算時(shí)間減少多于一半。之所以會(huì)出現(xiàn)超線性并行可擴(kuò)展性是因?yàn)槭褂肔U分解算法求解子問題，而LU算法的計(jì)算量是o（n3），其中n是求解問題的規(guī)模，也就是說當(dāng)子問題的規(guī)模減少一半時(shí)，子問題求解時(shí)間的減少量要遠(yuǎn)大于一半。由于并行計(jì)算時(shí)處理器之間需要進(jìn)行數(shù)據(jù)傳輸，當(dāng)處理器數(shù)目增加時(shí)，數(shù)據(jù)傳輸所需的時(shí)間也隨之增加，這就使得處理器核數(shù)較多時(shí)，NKS并行算法不一定會(huì)有線性或超線性并行可擴(kuò)展性。NKS算法求解兩幅灰度圖像復(fù)原問題的全變分模型時(shí)，具有線性甚至超線性加速比。

表1 NKS算法關(guān)于lenna和boat灰度圖像的并行可擴(kuò)展性

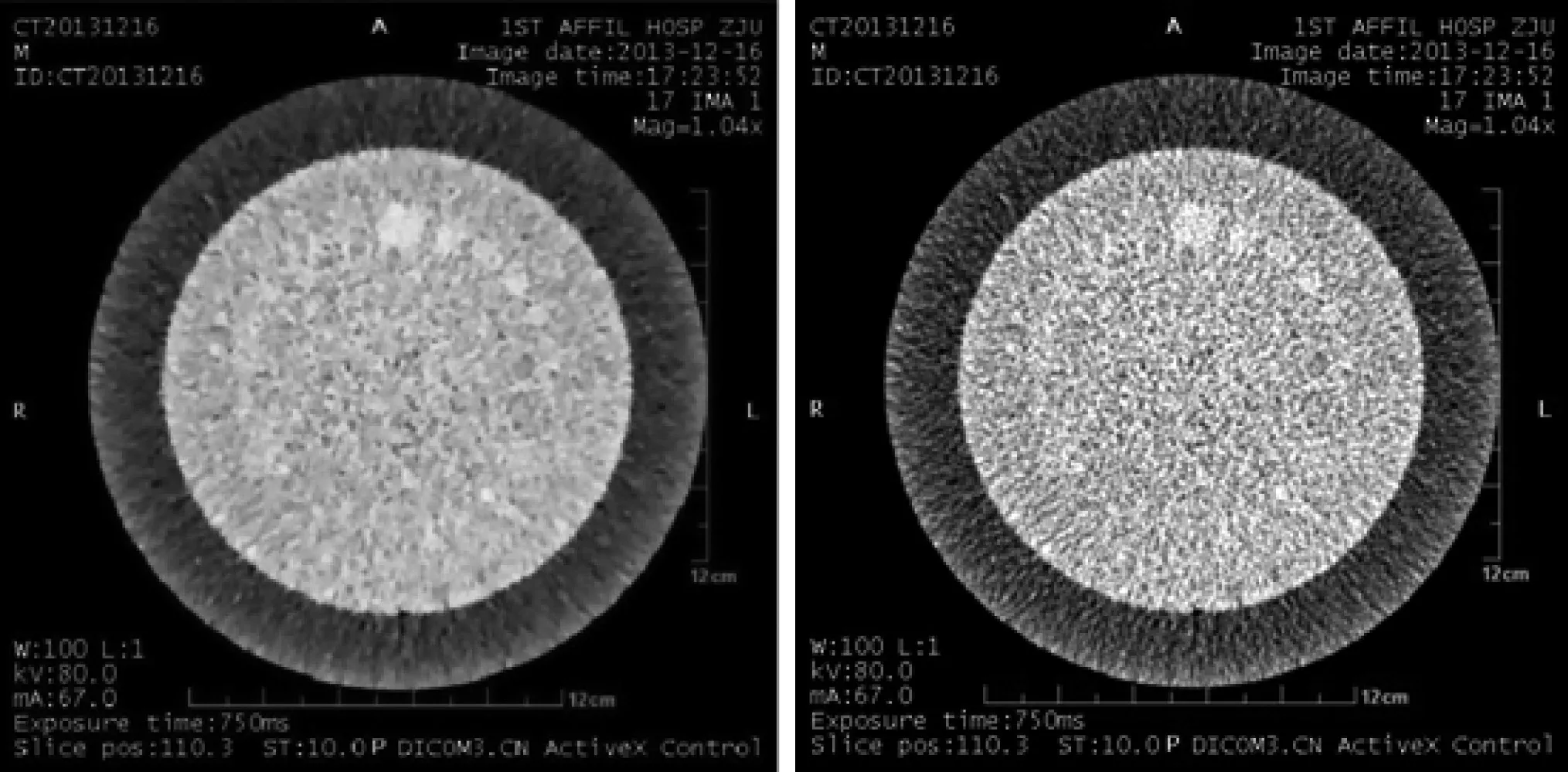
圖1：左圖是原始的67mA圖，將其看作原始的待去噪的圖像，右圖是算法下獲得的去噪圖像

4 總結(jié)

本文的研究工作圍繞圖像復(fù)原的變分PDE模型展開，針對(duì)大規(guī)模圖像復(fù)原問題，結(jié)合非精確Newton法和區(qū)域分解技術(shù)，構(gòu)造模型的NKS并行求解算法，并且對(duì)比、分析、驗(yàn)證算法的有效性，測(cè)試算法的并行可擴(kuò)展性。文章深入研究了這套算法的各個(gè)部分，重點(diǎn)研究區(qū)域分解算法，建立一套適用于超級(jí)計(jì)算機(jī)的求解大規(guī)模圖像復(fù)原問題的可擴(kuò)展并行算法。依托超級(jí)計(jì)算機(jī)，針對(duì)灰度圖像的變分PDE模型，分別測(cè)試了NKS算法的收斂性和并行可擴(kuò)展性，驗(yàn)證了NKS算法并行求解基于變分PDE模型的圖像復(fù)原問題的有效性。

[1] Rudin LI，Osher S，F(xiàn)atemi E． Nonlinear total variation based noise removal algorithms[J]． Physica D：Nonlinear Phenomena，1992，60（1）：259-268．

[2] Xu J，Tai XC，Wang LL． A two-level domain decomposition method for image restoration[J]． UCLA Computational and Applied Mathematics Report，2010，4（3）：523-545．

[3] Cai XC，Li X． Inexact Newton methods with restricted additive Schwarz based nonlinear elimination for problems with high local nonlinearity[J]． SIAM Journal on Scientific Computing，2011，33（2）：746-762．

[4] XC C，M． D，M． S． Restricted additive Schwarz preconditioners with harmonic overlap for symmetric positive definite linear systems[J]． SIAM Journal on Numerical Analysis，2003，41（4）：1209-1231．

[5] Saad Y． Iterative methods for sparse linear systems[M]． Siam，2003：12-15．

[6] Prudencio EE，Byrd R，Cai XC． Parallel Full Space SQP Lagrange-Newton-Krylov-Schwarz Algorithms for PDE-Constrained Optimization Problems[J]． SIAM Journal on Scientific Computing，2006，27（4）：1305-1328．

[7] Barker AT，Cai XC． Scalable parallel methods for monolithic coupling in flui–structure interaction with application to blood flow modeling[J]． Journal of computational physics，2010，229（3）：642-659．

[8] Frommer A，Szyld DB． An algebraic convergence theory for restricted additive Schwarz methods using weighted max norms[J]． SIAM Journal on Numerical Analysis，2001，39（2）：463-479．

Application of Image Restoration Technique in Low Dose CT Image Denoising

LI Zhengding Department of Equipment, Hangzhou First People's Hospital,Hangzhou Zhejiang 310006, China

ObjectiveTo introduce a parallel technique for large scale image recovering and the application of it to the denoise of the low dosage CT iamges.MethodsAparallel Newton-Krylov-Schwarz method, based on the inexact Newton method, domain decomposition method and ROF model, is used to solve the large scale image recovering problems.ResultsFor the large scale images, the numerical results show that the proposed method has a good convergence, stability, and scalability. Low dose of CT after processing of low resolution images is significantly better than the untreated image.Conclusion(1) The recovering results are comparable with the results obtained by other methods in terms of accuracy; (2) The proposed method is much faster than the existing image denoising algorithms in terms of the total compute time; (3)the proposed algorithm can handle large scale image.

ROF model; low dosage CT image; domain decomposition method

TP391

A

1674-9316（2017）23-0135-03

10．3969/j．issn．1674-9316．2017．23．067

杭州市第一人民醫(yī)院設(shè)備科，浙江 杭州 310006